This paper is divided into four sections – A, B, C and D.
Answer all questions.
Section A consists of one question having sub-parts of one mark each.
Section B consists of seven questions of two marks each.
Section C consists of nine questions of three marks each, and
Section D consists of three questions of five marks each
.
Internal choices have been provided in two questions each in Section B,
Section C and Section D.
The intended marks for questions are given in brackets [ ].
All working, including rough work, should be done on the same sheet as and
adjacent to the rest of the answer.
Answers to sub parts of the same question must be given in one place only.
A list of useful physical constants is given at the end of this paper.
A simple scientific calculator without a programmable memory may be used for
calculations.
Section-A
Section - A consists of 20 questions of 1 mark each.
Question
1
Let E be an event such that P(not E) =1/5, then P(E) is equal to :
(a) 1/5
(b) 2/5
(c) 0
(d) 4/5
View
Solution
Question
2
If p (x) = x2 + 5x + 6, then p (-2) 1s:
(a) 20
(b) 0
(c) -8
(d) 8
View
Solution
Question
3
The mode of the numbers 2, 3, 3, 4,5, 4,4, 5, 3,4, 2, 6, 7 is:
(a) 2
(b) 3
(c) 4
(d) 5
View
Solution
Question
4
How many tangents can be drawn to a circle from a point on it?
(a) One
(b) Two
(c) Infinite
(d) Zero
View
Solution
Question
5
A quadratic equation whose one root is 2 and the sum of whose roots is
zero, is:
(a) x2+4=0
(b) x2-2=0
(c) 4x2-1=0
(d) x2-4=0
View
Solution
Question
6
Which of the following is not a quadratic equation ?
(a) 2(x-1)2 =4x2 - 2x + 1
(b) 2x - x2 =x2 + 5
(c) (√2x +√3)2 + x2= 3x2 - 5x
(d) (x2 +
2x)2=x4+3+4x3
View
Solution
Question
7
A quadratic polynomial whose sum and product of zeroes are 2 and -1
respectively is :
(a) x2+2x+1
(b) x2-2x-1
(c) x2+2x-1
(d) x2
-2x+1
View
Solution
Question
8
(HCF * LCM) for the numbers 30 and 70 is -
(a) 2100
(b) 21
(c) 210
(d) 70
View
Solution
Question
9
The length of the arc of a circle of radius 14 cm which subtends an angle of
60° at the centre of the circle is:
(a) 44/3 cm
(b) 88/3 cm
(c) 308/3 cm
(d) 616/3 cm
View
Solution
Question
10
If the radius of a semi-circular protractor is 7cm, then its perimeter is:
(a) 11 cm
(b) 14cm
(c) 22cm
(d) 36cm
View
Solution
Question
11
The angle of elevation of the top of a 15 m high tower at a point 15√3m away from the base of the
tower is :
(a) 30°
(b) 45°
(c) 60°
(a) 90°
View
Solution
Question
12
(2/3 sin 0° -4/5 cos0°) is equal to:
(a) 2/4
(b) -4/5
(c) 0
(d) -2/15
View
Solution
Question
13
From a well-shuffled deck of 52 cards, a card is drawn at random. What is
the probability of getting king of hearts ?
(a) 1/52
(b) 1/26
(c) 1/13
(d) 12/13
View
Solution
Question
14
The number (5-3√5+√5) is:
(a) an integer
(b) rational number
(c) an irrational number
(d) a whole number
View
Solution
Question
15
If the pair of linear equations x -y = 1, x + ky =5 has a unique solution
x = 2, y= 1, then the value of k is :
(a) - 2
(b) -3
(c) 3
(d) 4
View
Solution
Question
16
If ▵ABC ~ ▵DEF and ∠A = 47°, ∠E = 83°, then ∠C is equal :
(a) 47°
(b) 50°
(c) 83°
(d) 130°
View
Solution
Question
17
The length of the tangent from an external point A to a circle, of radius
3 cm, is 4 cm. The distance of A from the centre of the circle is:
(a) 7cm
(b) 5cm
(c) √7cm
(d) 25cm
View
Solution
Question
18
The pair of linear equations x + 2y + 5 = 0 and -3x-6y + 1=0 has:
(a) aunique solution
(b) exactly two solutions
(c) infinitely many solutions
(d) no solution
View
Solution
Questions number 19 and 20 are Assertion and Reason based questions carrying
1 mark each. Two statements are given, one labelled as Assertion (A) and the
other is labelled as Reason (R). Select the correct answer to these questons from the codes (a), (b),
(c) and (d) as given below.
(a) both Assertion (A) and Reason (R) are true and Reason (R) is the
correct explanation of the Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not
the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) is true.
Question
19
Assertion (A) : If one root of the quadratic equation 4x2-10x+(k—4)=0 is reciprocal of the
other, then value of k is 8.
Reason (R) : Roots of the quadratic equation x2-x + 1 =0 are real.
View
Solution
Question
20
Assertion (A) : A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R) : The lengths of tangents drawn from an external point to a
circle are equal.
View
Solution
Section-B
Section - B comprises of Very Short Answer (VSA) questions of 2 marks each.
Question
21
(A) Find the discriminant of the quadratic equation 3x2 — 2x + 1/3 = 0 and
hence find the nature of its roots.
OR
(B) Find the roots of the quadratic equation x2 -x-2=0.
View
Solution
Question
22
In the adjoining figure, A, B and C are points on
OP, OQ and OR respectively such that AB||PQ and :
AC||PR. Show that BC||QR.
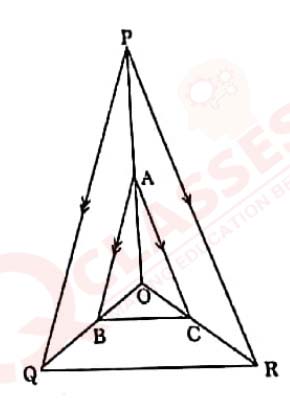
View
Solution
Question
23
If sin α=1/2,then find the value of (3 cos α -4 cos3α)
View
Solution
Question
24
(A) Find the coordinates | o “ a which divides the join of
A(-1, 7) and B (4, -3) in the ratio 2:3
OR
(B) If the points A(2,3),B(-5,6),C(6,7) and D (p,4) are the vertices of a parallelogram ABCD,find the
value of p.
View
Solution
Question
25
PA and PB are tangents drawn to the circle with center O as shown in the figure. Prove that ∠APB=2
∠OAB
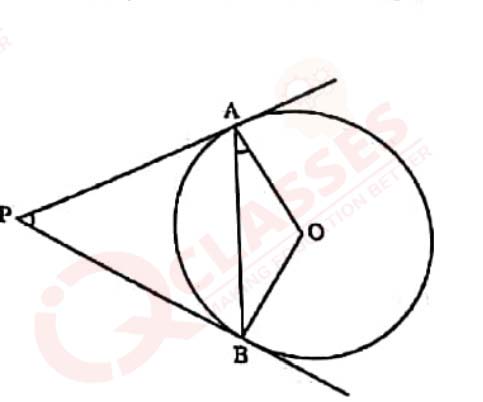
View
Solution
Section-C
This section comprises short answer (SA) type questions of 3 marks each.
Question
26
Find the area of the sector of a circle of radius 7 cm and of central angle 90°.Also,find the area
of corresponding major sector
View
Solution
Question
27
If α, β of the quadratic polynomial x2- 5x+6,form another quadratic polynomial
whose zeroes are 1/α,1/β
View
Solution
Question
28
A die is rolled once. Find the probability of getting:
(i) an even prime number. (ii) anumber greater than 4, (111) an odd number.
View
Solution
Question
29
Question
30
(A) Prove that the lengths of tangents drawn from an external point to a circle are equal.
OR
(B) Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the
larger circle which touches the smaller circle at P
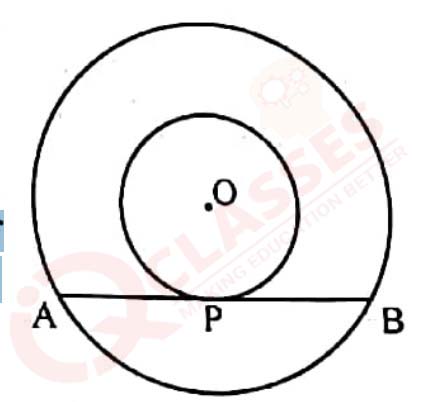
View
Solution
Question
31
(A) If we add 1 to the numerator and subtract 1 from the denominator, a
fraction reduces to 1. It becomes 1/2 if we only add 1 to the
denominator, What is the fraction ?
OR
(B) For which value of 'k' will the following pair of linear equations have
no solution ?
3x + y=1
(2k—1)x+(k-1)y=2k+1
View
Solution
Question
32
(A) Find the sum of first 51 terms of an A.P. whose second and third terms are 14 and 18, respectively,
OR
(B) The first term of an A.P. is 5,the last term is 45 and the sum is 400.Find the number of terms and
the common difference
View
Solution
Question
33
The distribution below gives the weight of 30 students of a class.Find the median weight of the
students:

View
Solution
Question
34
The boilers are used in thermal power plants to store water and then used to produce steam. One such
boiler
consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7m and radius of
cylindrical part is 7/2m
Find the total surface area and the volume of the
boiler. Also, find the ratio of the volume of cylindrical
part to the volume of one hemispherical part.
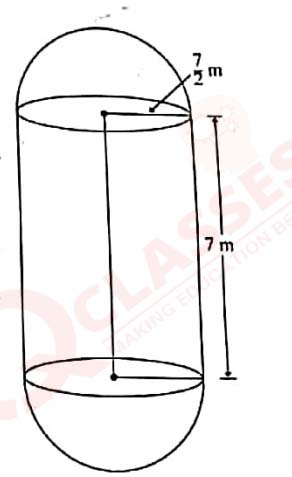
View
Solution
Question
35
(A) The shadow of a tower standing on a level ground is found to be 40 m
longer when the Sun’s altitude is 30° than when it was 60°. Find the
height of the tower.
OR
(B) From the top of a7 m high building, the angle of elevation of the top of
a cable tower is 60° and the angle of depression of its foot is 45°.
Determine the height of the tower.
View
Solution
Section-E
This section comprises 3 case study based questions of 4 marks each.
Question
36
Question
37
Use of Mobile screen for long hours makes your eye sight weak and give you headaches.Children who
addicted to play "PUBG" can get easily
stressed out. To raise social awarness about ill effects of playing PUBG,a school decided to start 'BAN
PUBG' campaign,in which students are asked to prepare campaign board in the shape of a rectangle.One
such campaign board made by class X student of the school is shown in the figure
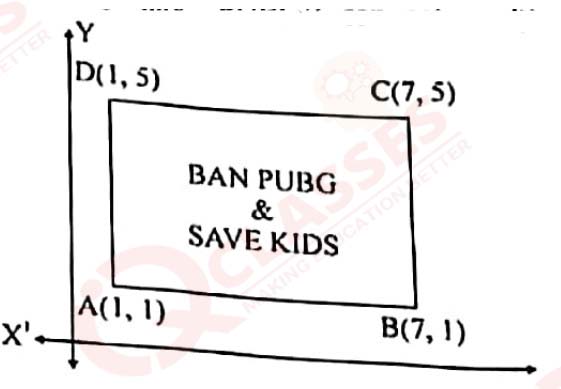
Based on the above information,answer the following questions:
(i) Find the coordinates of the point of intersection of diagonals AC and BD.
(ii)Find the length of the diagonal AC.
(iii) (a) Find the area of the campaign board ABCD
OR
(b) Find the ratio of the length of side AB to the length of the diagonal AC.
View
Solution
Question
38
Khushi wants to organize her birthday party. Being health conscious, she decided to serve only fruits in
her birthday party. She bought 36 apples and 60 bananas and decided to distribute fruits equally among
all.
Based on the above information, answer the following questions :
(i) How many guests Khushi can invite at the most ?
(ii) How many apples and bananas will each guest get ?
(iii) (a) If Khushi decides to add 42 mangoes, how many guests Khushi can
invite at the most?
OR
(b) If the cost of 1 dozen of bananas is ₹60, the cost of 1 apple is ₹15
and cost of 1 mango is ₹20, find the total amount spent on
60 bananas, 36 apples and 42 mangoes,
View
Solution