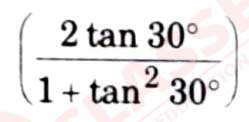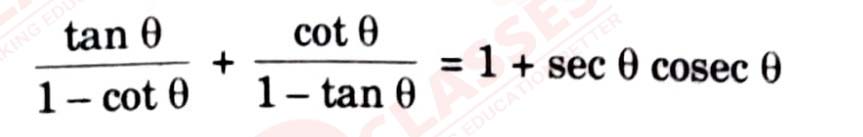This paper is divided into four sections – A, B, C and D.
Answer all questions.
Section A consists of one question having sub-parts of one mark each.
Section B consists of seven questions of two marks each.
Section C consists of nine questions of three marks each, and
Section D consists of three questions of five marks each
.
Internal choices have been provided in two questions each in Section B,
Section C and Section D.
The intended marks for questions are given in brackets [ ].
All working, including rough work, should be done on the same sheet as and
adjacent to the rest of the answer.
Answers to sub parts of the same question must be given in one place only.
A list of useful physical constants is given at the end of this paper.
A simple scientific calculator without a programmable memory may be used for
calculations.
Section-A
This section comprises multiple choice questions (MCQs) of 1 mark each
Question
1
The number of polynomials having zeroes-3 and 5 is:
(a) only one
(b) infinite
(c) exactly two
(d) at most two
View
Solution
Question
2
The pair of equations ax + 2y = 9 and 3x + by = 18 represent parallel lines, where a, b are integers,
if:
(a) a = b
(b) 3a = 2b
(c) 2a=3b
(d) ab = 6
View
Solution
Question
3
The common difference of the A.P. whose nth term is given by an = 3n + 7,
is:
(a) 7
(b) 3
(c) 3n
(d) 1
View
Solution
Question
4
In the given figure, DE || BC. The value of x is:
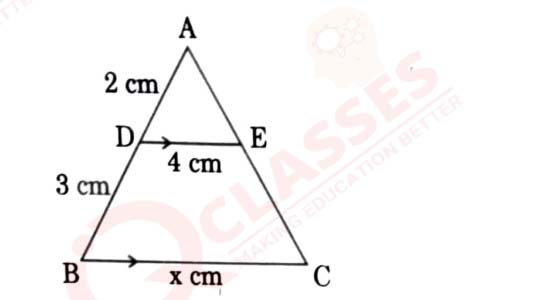
(a) 6
(b) 125
(c) 8
(d) 10
View
Solution
Question
5
A quadratic equation whose roots are (2 + √3) and (2- √3) is
(a) x2-4x+1=0
(b) x2+4x+1=0
(c) 4x2 -3=0
(d) x2 -1=0
View
Solution
Question
6
If tan θ =5/12, then the value of sinθ + cosθ/sinθ - cosθ is:
(a) -17/7
(b) 17/7
(c) 17/13
(d) -7/13
View
Solution
Question
7
The distance between the points P(-11/3,5) and Q (-2/3,5) is:
(a) 6 units
(b) 4 units
(c) 2 units
(d) 3 units
View
Solution
Question
8
In the given figure, AB = BC = 10 cm. If AC = 7 cm, then the length of BP
is:
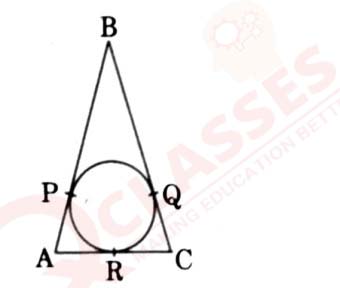
(a) 35 cm
(b) cm
(c) 6.5 cm
(d) 5 cm
View
Solution
Question
9
Water in a river which is 3 m deep and 40 m wide is tlowing at the rate of
2 km/h. How much water will fall into the sea in 2 minutes ?
(a) 800 m3
(b) 4000 m3
(c) 8000 m3
(d) 2000 m3
View
Solution
Question
10
If the mean and the median of a data are 12 and 15 respectively, then its
mode is:
(a) 13.5
(b) 21
(c) 6
(d) 14
View
Solution
Question
11
In the given figure, AB is a tangent to the circle centered at 0. If
OA = 6 cm and ∠ OAB = 30°, then the radius of the circle is
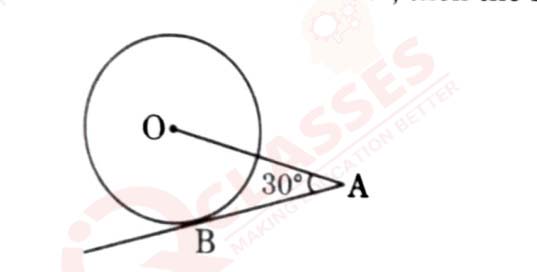(a) 3 cm
(b) 3√3 cm
(c) 2 cm
(d) 3 cm
View
Solution
Question
12
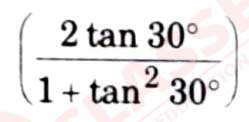
is equal to:
(a) sin 60°
(b) cos 60°
(c) tan 60°
(d) sin 30°
View
Solution
Question
13
In ▵ ABC and ▵ DEF, AB/DE=BC/FD . Which of the following makes the two triangles
similar?
(a) ∠ A= ∠ D
(b) ∠ B= ∠ D
(c) ∠ B= ∠ E
(d) ∠ A = ∠ F
View
Solution
Question
14
The 11th term from the end of the A.P. : 10, 7,4, .., -62 is:
(a) 25
(b) 16
(c) - 32
(d) 0
View
Solution
Question
15
Two coins are tossed together. The probability of getting at least one tail
is:
(a) 1/4
(b) 1/2
(c) 3/4
(d) 1
View
Solution
Question
16
In the given figure, AC and AB are tangents to a circle centered at O. If
∠COD = 120°, then ∠ BAO is equal to
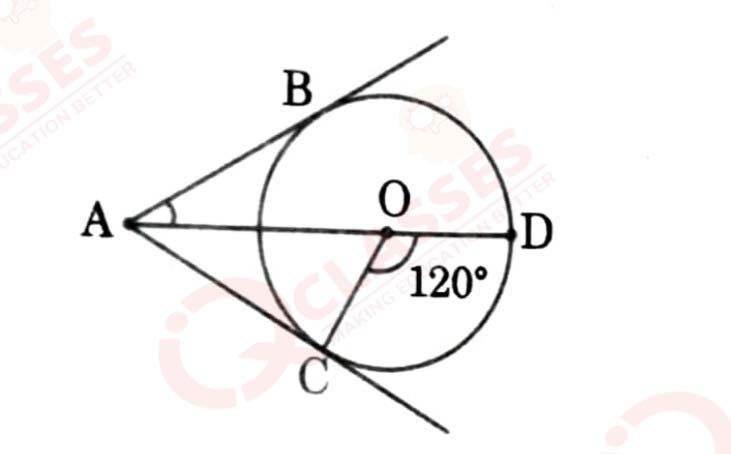
(a) 30°
(b) 60°
(c) 45°
(d) 90°
View
Solution
Question
17
Which of the following numbers cannot be the probability of happening of an event?
(a) 0
(b) 7/0.01
(c) 0.07
(d) 0.07/3
View
Solution
Question
18
If every term of the statistical data consisting of n terms is decreased by 2, then the mean of the
data:
(a) decreases by 2
(b) remains unchanged
(c) decreases by 2n
(d) decreases by 1
View
Solution
Questions number 19 and 20 are Assertion and Reason based questions carrying
1 mark each. Two statements are given, one labelled as Assertion (A) and the
other is labelled as Reason (R). Select the correct answer to these questons from the codes (a), (b),
(c) and (d) as given below.
(a) both Assertion (A) and Reason (R) are true and Reason (R) is the
correct explanation of the Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not
the correct explanation of the Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) is true.
Question
19
Assertion (A): If the points A(4, 3) and B(x, 5) lie on a circle with centre
O(2,3), then the value of x is 2.
Reason (R): Centre of a circle is the mid-point of each chord of the
circle.
View
Solution
Question
20
Assertion (A): The number 5n cannot end with the digit 0, where n is a
natural number.
Reason (R): Prime factorisation of 5 has only two factors, 1 and 5.
View
Solution
Section-B
This section comprises very short answer (VSA) type questions of 2 marks each.
Question
21
(a) The line segment joining the points A(4, -5) and B(4, 5) is divided
by the point P such that AP: AB = 2:5. Find the coordinates of P.
OR
(b) Point P(x, y) is equidistant from points A(5, 1) and B(1, 5). Prove
that x = y.
View
Solution
Question
22
In the given figure, PT is a tangent to the circle centered at O, OC is
perpendicular to chord AB. Prove that PA. PB = PC2 - AC2
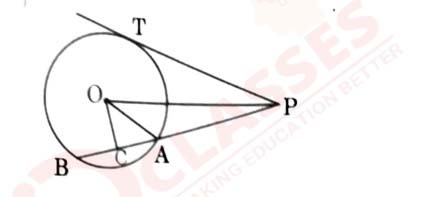
View
Solution
Question
23
Using prime factorisation, find HCF and LCM of 96 and 120.
View
Solution
Question
24
Find the ratio in which y-axis divides the line segment joining the points
(5,-6) and (-1,-4).
View
Solution
Question
25
(a) If a cos θ + b sin θ = m and a sin θ - b cos θ = n, then prove that
a2+b2 = m2 + n2
OR
(b) Prove that:
View
Solution
Section-C
This section comprises short answer (SA) type questions of 3 marks each.
Question
26
(a) Prove that √3 is an irrational number.
(b) The traffic lights at three different road crossings change after
every 48 seconds, 72 seconds and 108 seconds respectively. If they
change simultaneously at 7 a.m., at what time will they change
together next?
View
Solution
Question
27
If pth term of an A.P. is q and qth term is p, then prove that its nth
term is
(p+q-n).
View
Solution
Question
28
(a) In the given figure, CD is the perpendicular bisector of AB. EF
perpendicular to CD. AE intersects CD at G. Prove that CF/CD=FG/DG
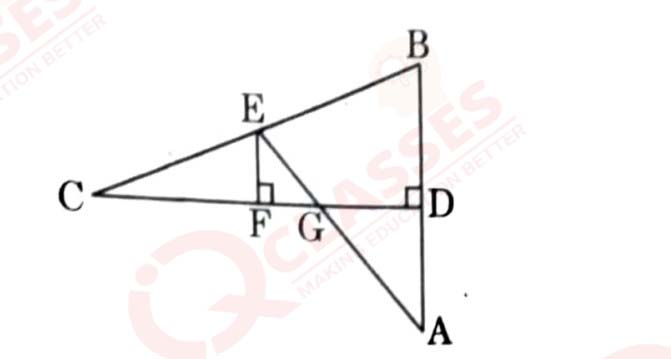
OR
(b) In the given figure, ABCD is a parallelogram. BE bisects CD at M
and intersects AC at L. Prove that EL = 2BL.
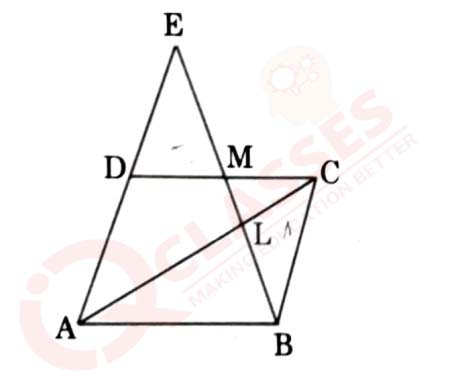
View
Solution
Question
29
Two people are 16 km apart on a straight road. They start walking at the
same time. If they walk towards each other with different speeds, they
will meet in 2 hours. Had they walked in the same direction with same
speeds as before, they would have met in 8 hours. Find their walking
speeds.
View
Solution
Question
30
Question
31
Find the mean of the following frequency distribution
View
Solution
Section-D
This section comprises long answer (LA) type questions of 5 marks eac h.
Question
32
One observer estimates the angle of elevation to the basket of a hot a
balloon to be 60°, while another observer 100 m away estimates the angie
of elevation to be 30°. Find:
(a) The height of the basket from the ground
(b) The distance of the basket from the first observer's eye
(c) The horizontal distance of the second observer from the basket.
View
Solution
Question
33
(a) A triangle ABC is drawn to cireumscribe a circle of radius 4 cm
such that the segments BD and DC are of lengths 10 cm and 8 cm
respectively. Find the lengths of the sides AB and AC, if it is given
that area A ABC = 90 cm2.
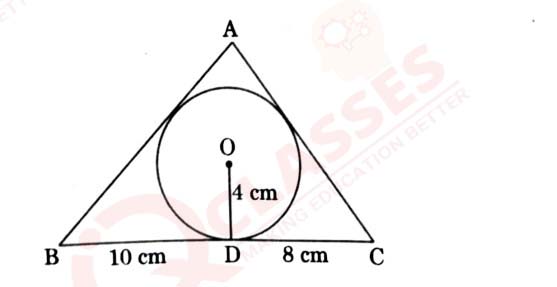
OR
(b) Two circles with centres O and O of radii 6 cm and 8 cm,
respectively intersect at two points P and Q such that OP and OP
are tangents to the two circles. Find the length of the common
chord PQ.
View
Solution
Question
34
(a) A train travels at a certain average speed for a distance of 54 km
and then travels a distance of 63 km at an average speed of 6 km/h
more than the first speed. If it takes 3 hours to complete the
journey, what was its first average speed?
(b) Two pipes together can fill a tank in 15/8 hours. The pipe with
larger diameter takes 2 hours less than the pipe with smaller
diameter to fill the tank separately. Find the time in which each
pipe can fill the tank separately.
View
Solution
Question
35
A horse is tied to a peg at one corner ofa square shaped grass field of side
15 m by means of a 5 m long rope. Find the area of that part of the field
in which the horse can graze. Also, find the increase in grazing area if
length of rope is inereased to 10 m. (Use π =3.14)
View
Solution
Section-E
This section comprises 3 case study based questions of 4 marks each.
Question
36
Case Study-I
A golf ball is spherical with about 300 500 dimples ts that help increase velocity while in play. Golf
balls are in traditionally white but availaDlie colours also. In the given figure, a golf ball has
diameter
4.2 cm and the surface has 315 dimples (hemi-spherical) of radius 2 mm.
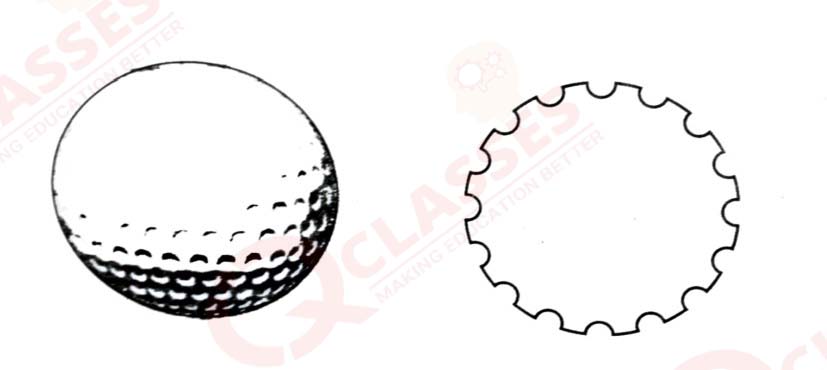
Based on the above, answer the following questions
(i) Find the surface area of one such dimple.
(ii) Find the volume of the material dug out to make one dimple
(iii) (a) Find the total surface area exposed to the surroundings
OR
(iii) (b) Find the volume of the golf ball.
View
Solution
Question
37
Case Study -2
A middle school decided to run the following spinner game as a fund-raiser on Christmas Carnival.
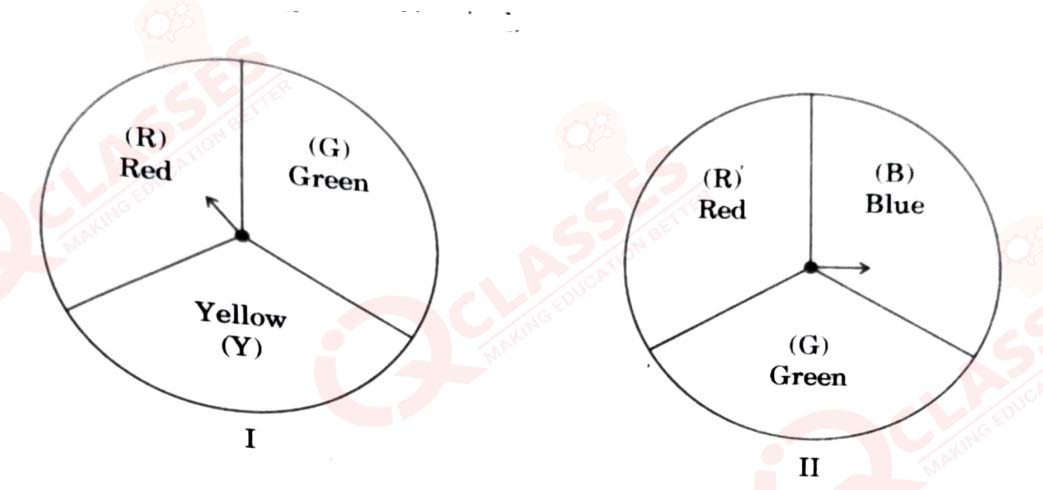
Making Purple : Spin each spinner once. Blue and red make one purple. So, if spinner shows Red (R) and
another Blue (B), then you 'win'. One such outcome is written as 'RB'
Based on the above, answer the following questions:
(i) List all possible outcomes of the game.
(ii) Find the probability of Making Purple'.
(iii)(a) For each win, a participant gets ₹10, but if he/she loses, he/she has to pay 5 to the school.
If 99 participants played, calculate how much fund could the
school have collected.
OR
(b) If the same amount of ₹5 has been decided for winning or
losing the game, then how much fund had been collected by school ? (Number of participants = 99)
View
Solution
Question
38
In a pool at an aquarium, a dolphin jumps out of the water travelling at 20 cm per second. Its height
above
water level after t seconds is given by
h=20t - 16t2.
Based on the above, answer the following questions :
(i) Find zeroes of polynomial p(t) = 20t -16 t2
(ii) Which of the following types of graph represents p(t) ?
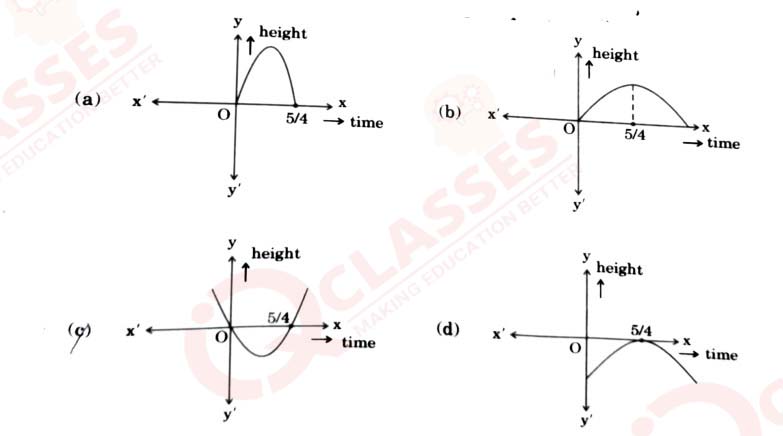
(iii) (a) What would be the value of h at t=3/2? Interpret the result.
OR
(iii) (b) How much distance has the dolphin covered before hitting
the water level again?
View
Solution
