Class 12 ISC Maths Boards Paper 2023

Maximum Marks: 70

Time Allowed: Three hours

(Candidates are allowed additional 15 minutes for only reading the paper.
They must NOT start writing during this time).

This paper is divided into four sections – A, B, C and D.

Answer all questions.

Section A consists of one question having sub-parts of one mark each.

Section B consists of seven questions of two marks each.

Section C consists of nine questions of three marks each, and

Section D consists of three questions of five marks each

. Internal choices have been provided in two questions each in Section B, Section C and Section D.

The intended marks for questions are given in brackets [ ].

All working, including rough work, should be done on the same sheet as and adjacent to the rest of the answer.

Answers to sub parts of the same question must be given in one place only.

A list of useful physical constants is given at the end of this paper.

A simple scientific calculator without a programmable memory may be used for calculations.

Section-A

Class 12 ISC Maths Boards Paper 2023

Section-A

Question 1

In subparts (i) to (x) choose the correct options and in subparts (xi) to (xv), answer the questions as instructed.

(i) A relation R on {1, 2, 3} is given by R= {(1, 1), (2, 2), (1, 2), (3, 3), (2, 39)}. Then the relation R is: (a) Reflexive. (b) Symmetric. (c) Transitive. (d) Symmetric and Transitive.

Solution

(ii) If A is a square matrix of order 3, then |2A| is equal to: (a) 2|A| (b) 4 |A| (c) 8|A| (d) 6|A|

Solution

(iii)If the following function is continuous at x = 2 then the value of k will be: (a) 2 (b) 3 (c) 5 (d) -1

Solution

(iv) An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long? (a) 75 cm3/sec (b) 750 cm3/sec (c) 7500 cm3/sec (d) 1250 cm3/sec

Solution

(v) Let f(x) = x3 be a function with domain {0, 1, 2, 3}. Then domain of f-1 is: (a) {3,2, 1,0} (b) {0,—1,—2,—3} (c) {0,1,8,27} (d) {0,—1,-8,—27}

Solution

(vi) For the curve y2 = 2x3 — 7, the slope of the normal at (2, 3) is: (a) 4 (b) 1/ 4 (c) -4 (d) -1/ 4

Solution

(vii) (a) 2log(x2+1)+c (b) 1/2log(x2 +1)+c (c) ex2 + 1 + C (d) log x + x2 /2 + c

Solution

(viii) The derivative of log x with respect to 1/x is: (a) 1/x (b) -1/x3 (c) -1/x (d) -x

Solution

(ix) The interval in which the function f(x) = 5 + 36x — 3x2 increases will be: (a) (-∞, 6) (b) (6, ∞) (c) (-6,6) (d) (0, —6)

Solution

(x) (a) ∞ (b) 1 (c) -1 (d) 0

Solution

(xi) Solve the differential equation: dy/dx = cosec y

Solution

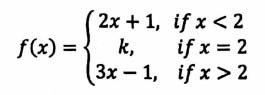
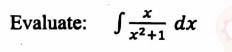
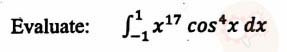
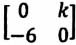(xii) For what value of k the matrix is a skew symmetric matrix?

Solution

(xiii)

Solution

(xiv)

Solution

(xv) A bag contains 19 tickets, numbered from 1 to 19. Two tickets are drawn randomly in succession with replacement. Find the probability that both the tickets drawn are even numbers.

Solution

Section-B

Question 2

(i) If f(x) = [4 — (x — 7)3]1/5is a real invertible function, then find f-1(x) OR (ii) Let A=R - {2} and B=R - {1}. If f: A → B is a function defined by f(x) = (x -1 )/(x -2) then show that f is a one — one and an onto function.

Solution

Question 3

Evaluate the following determinant without expanding.

Solution

Question 4

The probability of the event A occurring is 1/3 and of the event B occurring is 1/2 If A and B are independent events, then find the probability of neither A nor B occurring.

Solution

Question 5

Solve for x : 5tan-1 x + 3cot-1x =2π

Solution

Question 6

(i) Evaluate: ∫ cos-1(sin x) dx OR (ii) If ∫ x5 cos(x6)dx = k sin(x6) + C, find the value of k.

Solution

Question 7

then prove that 24x2 — 23x -12=0

Solution

Question 8

If y = eax cos bx, then prove that

Solution

Question 9

Solution

Question 10

(i) Solve the differential equation: (1+ y2) dx = (tan-1y — x)dy OR (ii) Solve the differential equation: (x2 — y2)dx + 2xy dy = 0

Solution

Question 11

Use matrix method to solve the following system of equations.

Solution

Question 12

Solution

Question 13

Solution

Question 14

A box contains 30 fruits, out of which 10 are rotten. Two fruits are selected at random one by one without replacement from the box. Find the probability distribution of the number of unspoiled fruits. Also find the mean of the probability distribution.

Solution

Section-B

Question 15

In subparts (i) and (ii) choose the correct options and in subparts (iii) to (v), answer the questions as instructed.

Solution

Question 16

Solution

Question 17

Solution

Question 18

(i) A relation R on {1, 2, 3} is given by R= {(1, 1), (2, 2), (1, 2), (3, 3), (2, 39)}.
Then the relation R is:
(a) Reflexive.
(b) Symmetric.
(c) Transitive.
(d) Symmetric and Transitive.

(ii) If A is a square matrix of order 3, then |2A| is equal to:
(a) 2|A|
(b) 4 |A|
(c) 8|A|
(d) 6|A|

(iii)If the following function is continuous at x = 2 then the value of k will be:

(a) 2
(b) 3
(c) 5
(d) -1

(iv) An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
(a) 75 cm³/sec
(b) 750 cm³/sec
(c) 7500 cm³/sec
(d) 1250 cm³/sec

(v) Let f(x) = x³ be a function with domain {0, 1, 2, 3}. Then domain of f^-1 is:
(a) {3,2, 1,0}
(b) {0,—1,—2,—3}
(c) {0,1,8,27}
(d) {0,—1,-8,—27}

(vi) For the curve y² = 2x³ — 7, the slope of the normal at (2, 3) is:
(a) 4
(b) 1/ 4
(c) -4
(d) -1/ 4

(vii)
(a) 2log(x²+1)+c
(b) 1/2log(x² +1)+c
(c) e^{x² + 1} + C
(d) log x + x² /2 + c

(viii) The derivative of log x with respect to 1/x is:
(a) 1/x
(b) -1/x³
(c) -1/x
(d) -x

(ix) The interval in which the function f(x) = 5 + 36x — 3x² increases will be:
(a) (-∞, 6)
(b) (6, ∞)
(c) (-6,6)
(d) (0, —6)

(x)
(a) ∞
(b) 1
(c) -1
(d) 0

(i) If f(x) = [4 — (x — 7)³]^1/5is a real invertible function, then find f^-1(x)
OR

(ii) Let A=R - {2} and B=R - {1}. If f: A → B is a function defined by f(x) = (x -1 )/(x -2) then show that f is a one — one and an onto function.

Solve for x :
5tan^-1 x + 3cot^-1x =2π

(i) Evaluate: ∫ cos^-1(sin x) dx
OR
(ii) If ∫ x⁵ cos(x⁶)dx = k sin(x⁶) + C, find the value of k.

then prove that 24x² — 23x -12=0

If y = e^ax cos bx, then prove that

(i) Solve the differential equation:
(1+ y²) dx = (tan^-1y — x)dy
OR
(ii) Solve the differential equation:
(x² — y²)dx + 2xy dy = 0

Find the area of the region bounded by the curve x² = 4y and the line x = 4y — 2

(i) The total cost function for x units is given by C(x) = √ (6x +5) + 2500. Show that the marginal cost decreases as the output x increases.
OR
(ii) The average revenue function is given by AR = 25 - x/4 Find total revenue function and marginal revenue function.

Solve the following Linear Programming Problem graphically.
Maximise Z = 5x + 2y subject to:
x—2y ≤ 2,
3x + 2y ≤ 12,
-3x + 2y ≤ 3,
x ≥ 0,y ≥ 0