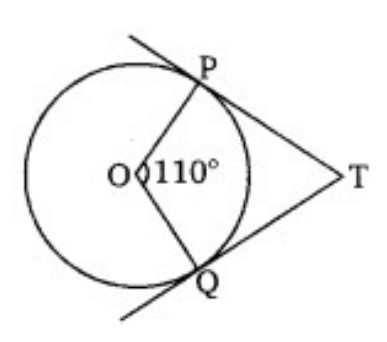
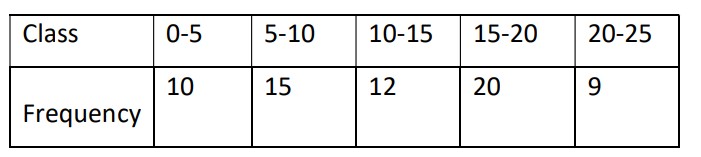
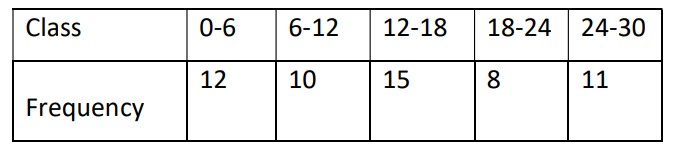
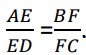Class 10 CBSE Maths Basic Specimen 2024
Maximum Marks: 80
Time Allowed: Three hours
This Question Paper has 5 Sections A, B, C, D, and E.
Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
Section E has 3 sourced based/Case Based/passage based/integrated units of
assessment (4 marks each) with sub-parts of the values of 1, 1 and 2 marks each
respectively.
All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs
of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has
been provided in the 2 marks questions of Section E.
Draw neat figures wherever required. Take π =22/7 wherever required if not
stated
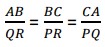 then
then