Class 10 ICSE Maths Specimen 2023

Maximum Marks: 80

Time allowed: Two and half hours

Answers to this Paper must be written on the paper provided separately.

You will not be allowed to write during first 15 minutes.

This time is to be spent in reading the question paper.

The time given at the head of this Paper is the time allowed for writing the answers.

Attempt all questions from Section A and any four questions from Section B.

All working, including rough work, must be clearly shown, and must be done on the same sheet as the rest of the answer.

Omission of essential working will result in loss of marks.

The intended marks for questions or parts of questions are given in brackets [ ]

Mathematical tables are provided.

Section-A

(Attempt all questions from this Section.)

Question 1

(i) The SGST paid by a customer to the shopkeeper for an article which is priced at Rs.500 is Rs.15. The rate of GST charged is:
(a) 1.5%
(b) 3%
(c) 5%
(d) 6%

Solution

(ii) When the roots of a quadratic equation are real and equal then the discriminant of the quadratic equation is:
(a) Infinite
(b) Positive
(c) Zero
(d) Negative

Solution

(iii) If (x — 1) is a factor of 2x² — ax — 1, then the value of 'a' is:
(a) -1
(b) 1
(c) 3
(d) -3

Solution

(iv)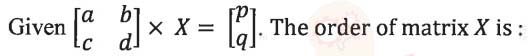
(a) 2x2
(b) 1x2
(c) 2x1
(d) 1x1

Solution

(v) 57, 54, 51, 48, ......... are in Arithmetic Progression. The value of the 8th term is:
(a) 36
(b) 78
(c) -36
(d) -78

Solution

(vi) The point A (p,q) is invariant about x = p under reflection. The coordinates of it's image A’ is:
(a) A’(p,—q)
(b) A'(—p, q)
(c) A’(p, q)
(d) A’(-p,-q)

Solution

(vii) In the given diagram the △ABC is similar to △DEF by the axiom:

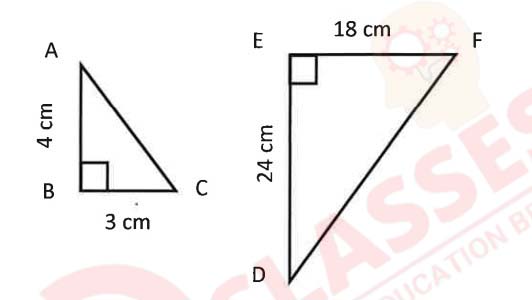
(a) SSS
(b) SAS
(c) AAA
(d) RHS

Solution

(viii) The volume of a right circular cone with same base radius and height as that of a right circular cylinder, is 120 cm³. The volume of the cylinder is:
(a) 240 cm²
(b) 60cm²
(c) 360 cm²
(d) 480 cm²

Solution

(ix) The solution set for the given in equation is: -8≤ 2x < 8, x ∈ W
(a) {-4, -3, -2, -1, 0, 1,2, 3, 4}
(b) {-4, -3, -2, -1}
(c) {0, 1,2, 3}
(d) {-8, -7, -6, -5, -4, -3, -2, -1, 0, 1,2, 3, 4, 5,6 7, 8}

Solution

(x) The probability of the Sun rising from the east is P(S). The value of P(S) is:
(a) P(S) = 0
(b) P(S) < 0
(c) P(S) = 1
(d) P(S) > 1

Solution

(xi)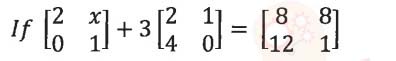
The value of x is:
(a) 2
(b) 3
(c) 4
(d) 5

Solution

(xii) The centroid of a △ABC is G (6, 7). If the coordinates of the vertices A, B and C are (a, 5), (7, 9) and (5, 7) respectively.
The value of a is:
(a) 9
(b) 6
(c) 3
(d) 7

Solution

(xiii) In the given diagram AC is a diameter of the circle and ∠ADB=35°

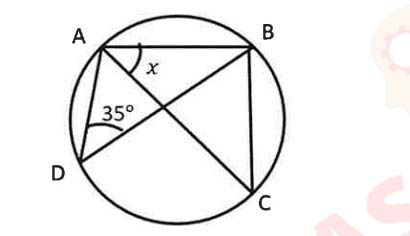
The value of x :
(a) 55°
(b) 35°
(c) 45°
(d) 70°

Solution

(xiv) If the nth term of an Arithmetic Progression (A.P.) is (n + 3), then the first three terms of the A.P. are:
(a) 1,2,3
(b) 2,4,6
(c) 4,5,6
(d) 7,8,9

Solution

(xv) The median of a grouped frequency distribution is found graphically by drawing:
(a) a linear graph
(b) a histogram
(c) a frequency polygon
(d) a cumulative frequency curve

Solution

Question 2

(i) Salman deposits Rs.1200 every month in a recurring deposit account for 2 1/2 years. If the rate of interest is 6% per annum, find the amount he will receive on maturity.
(ii) 3, 9, m, 81 and n are in continued proportion. Find the values of m and n.
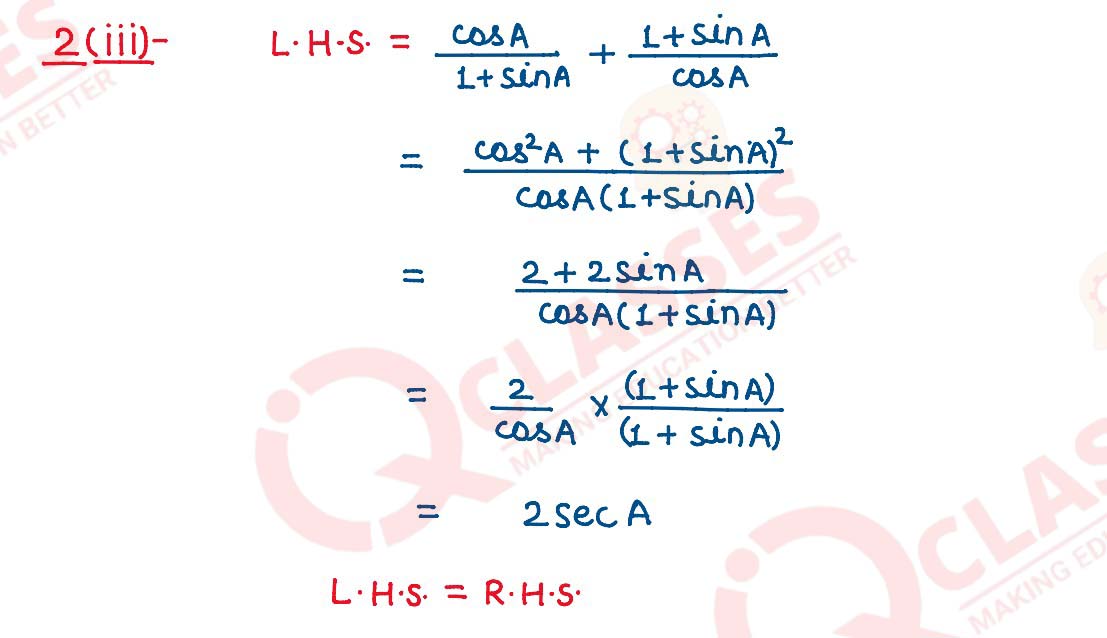
(iii)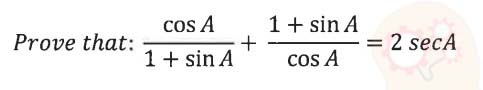

Solution

Question 3

(i) The inner circumference of the rim of a circular metal tub is 44 cm.

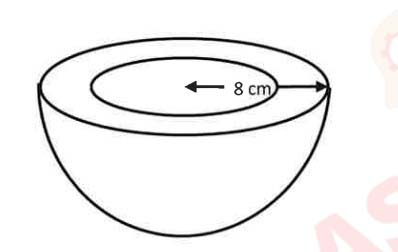
Find:
(a) The inner radius of the tub
(b) The volume of the material of the tub if it’s outer radius is 8 cm.
Use π = 22/7
Give your answer correct to three significant figures.

(ii) From the given figure:

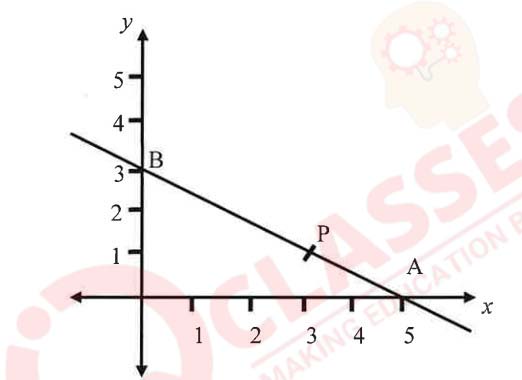
(a) Write down the coordinates of A and B.
(b) If P divides AB in the ratio 2:3, find the coordinates of point P
(c) Find the equation of a line parallel to line AB and passing through origin.

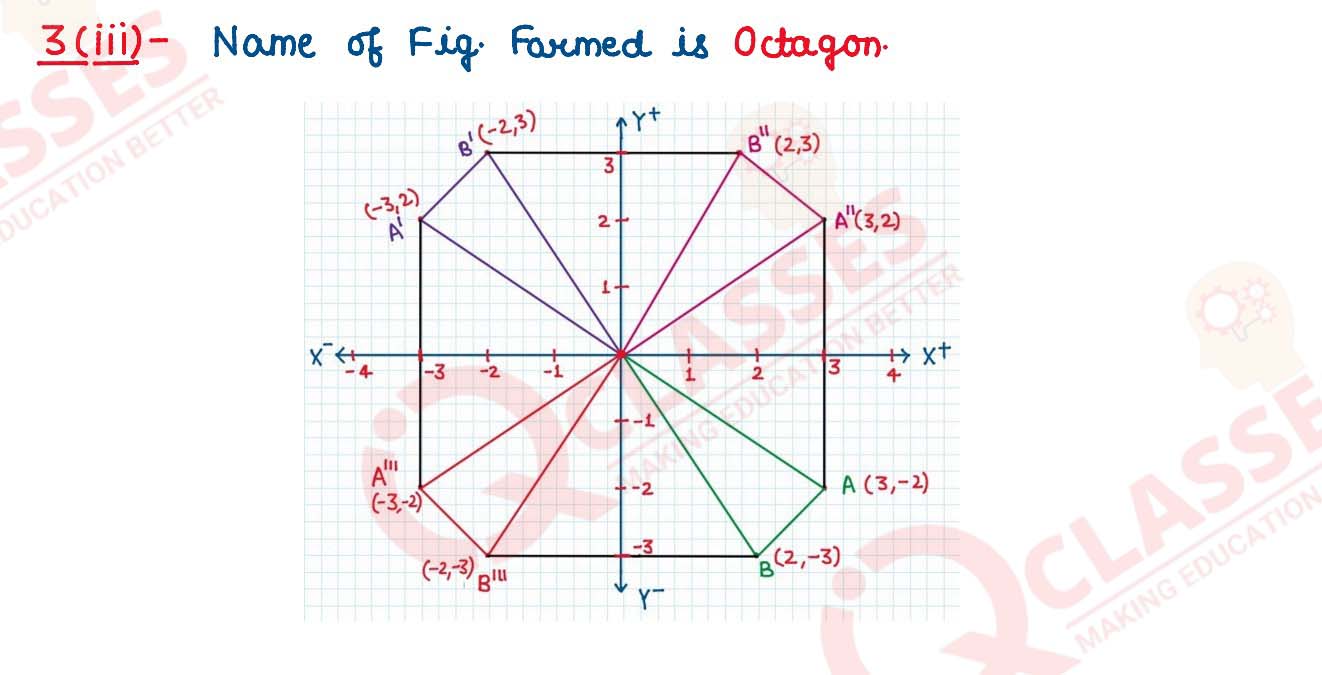
(iii) Use graph sheet for this question. Take 2 cm = 1 unit along the axes.
Plot the △OAB, where O (0,0), A(3, -2), B (2, -3).
(a) Reflect the △OAB through the origin and name it as △OA’B’.
(b) Reflect the △OA’B’on the y — axis and name it as △OA''B”.
(c) Reflect the △OA'B’on the x — axis and name it as △OA'''B'''.
(d) Join the points AA'’B"B'A'A'''B'''B and give the geometrical name of the closed figure so formed.

Solution

Section-B

(Attempt any four questions from this Section.)

Question 4

(i) The following bill shows the GST rates and the marked price of articles:

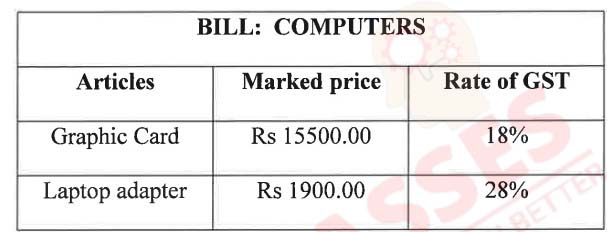
Find the total amount to be paid for the above bill.

(ii) Solve the following quadratic equation,
7x²+ 2x - 2 = 0
Give your answer correct to two places of decimal

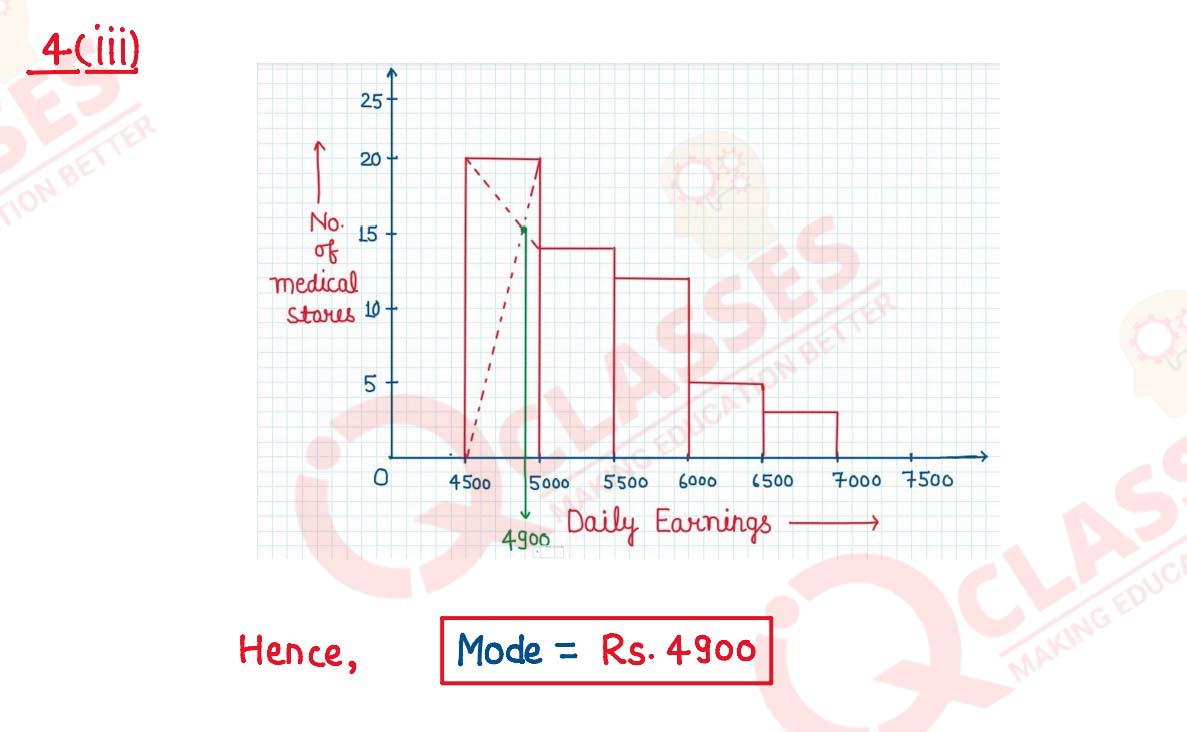
(iii) Use graph sheet for this question. Draw a histogram for the daily earnings of 54 medical stores in the following table and hence estimate the mode for the following distribution. Take 2 cm = Rs.500 units along the x-axis and 2 cm = 5 stores along the y-axis.

Solution

Question 5

(i)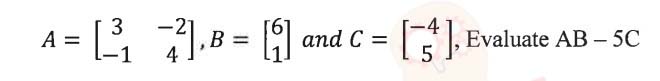

(ii) In the given figure, O is the centre of circle. The tangent PT meets the diameter RQ produced at P.

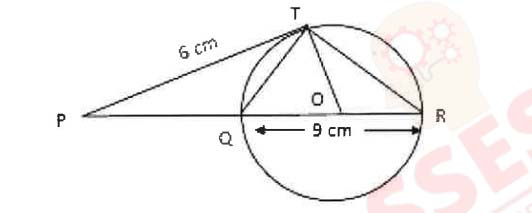
(a) Prove △PQT ~ △PTR
(b) If PT =6cm,QR =9 cm. Find the length of PQ

(iii) Factorise the given polynomial completely, using Remainder Theorem:
6x³ + 25x² + 31x+10

Solution

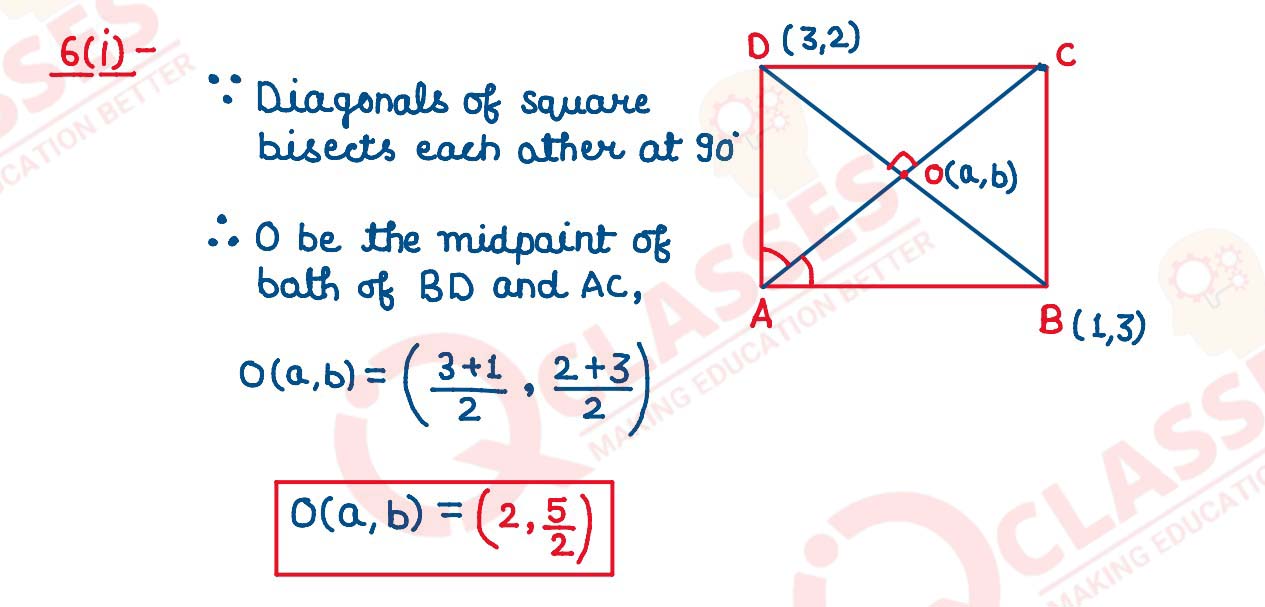
Question 6

(i) ABCD is a square where B (1, 3), D (3, 2) are the end points of the diagonal BD. Find:
(a) the coordinates of point of intersection of the diagonals AC and BD
(b) the equation of the diagonal AC

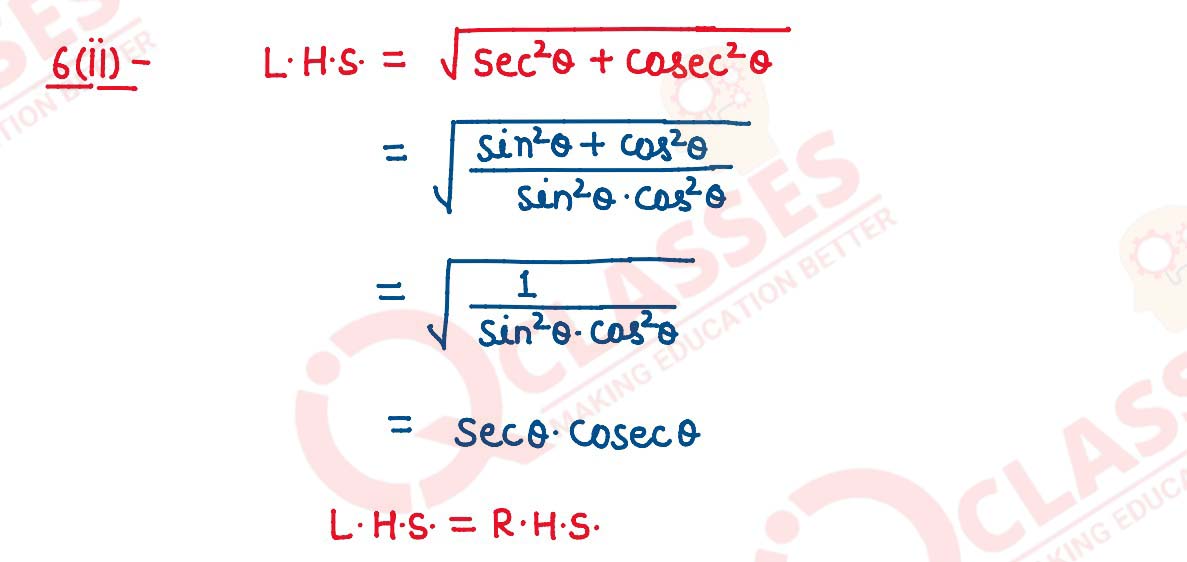
(ii)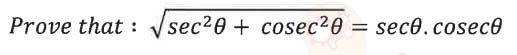

(iii) The first, the last term and the common difference of an Arithmetic Progression are 98, 1001 and 7 respectively. Find the following for the given Arithmetic Progression:
(a) number of terms ‘n’.
(b) Sum of the ‘n’ terms.

Solution

Question 7

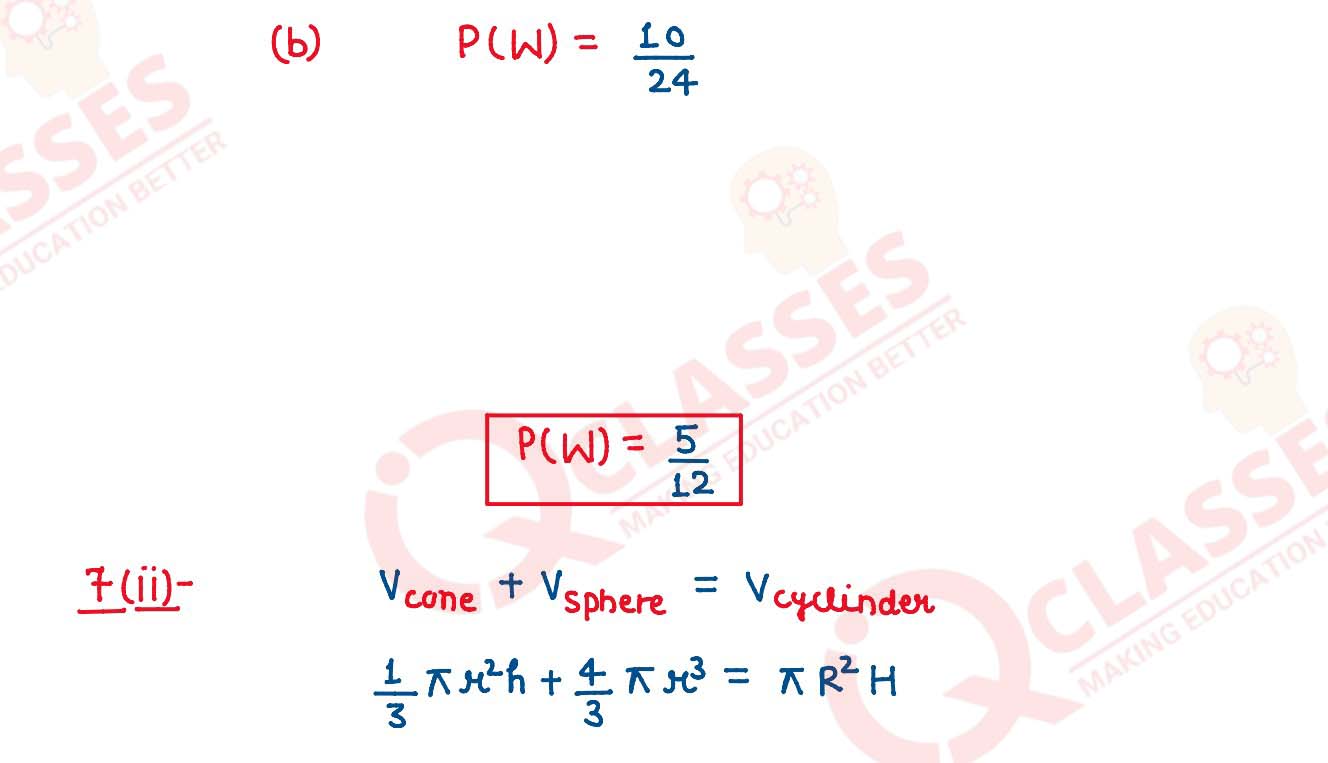
(i) A box contains some green, yellow and white tennis balls. The probability of selecting a green ball is 1/4 and yellow ball is 1/3. If the box contains 10 white balls, then find:
(a) total number of balls in the box.
(b) probability of selecting a white ball.

(ii) A cone and a sphere having the same radius are melted and recast into a cylinder. The radius and height of the cone are 3 cm and 12 cm respectively. If the radius of the cylinder so formed is 2 cm, find the height of the cylinder.

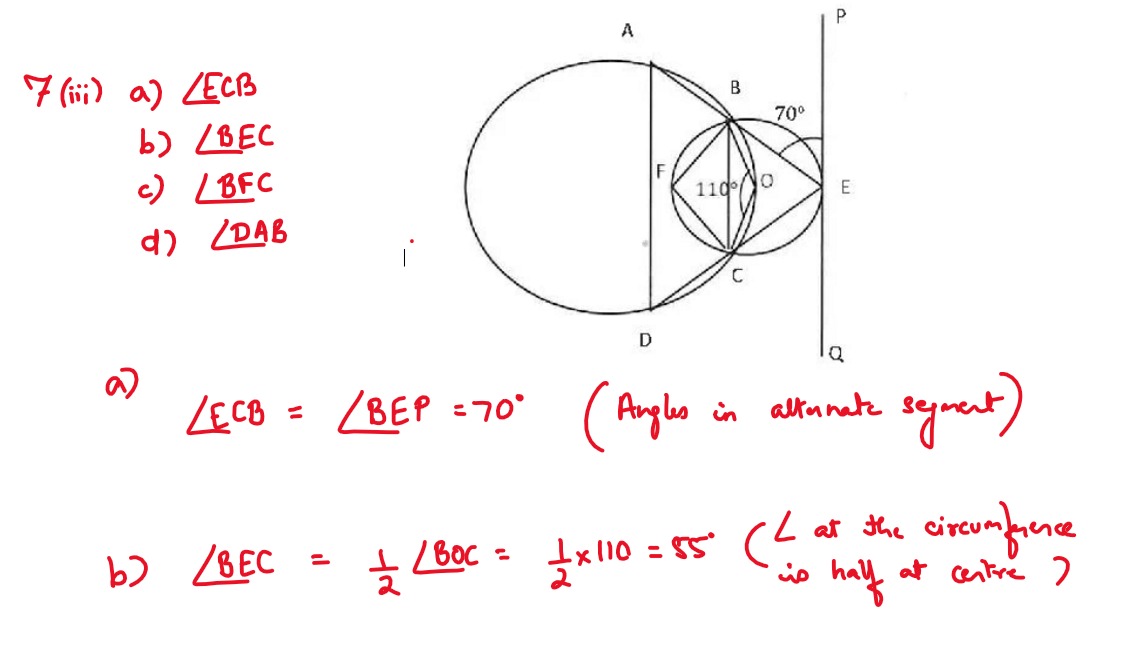
(iii) In the given diagram, ABCD is a cyclic quadrilateral and PQ is a tangent to the smaller circle at E. Given ∠AEP = 70°, ∠ BOC = 110°. Find:

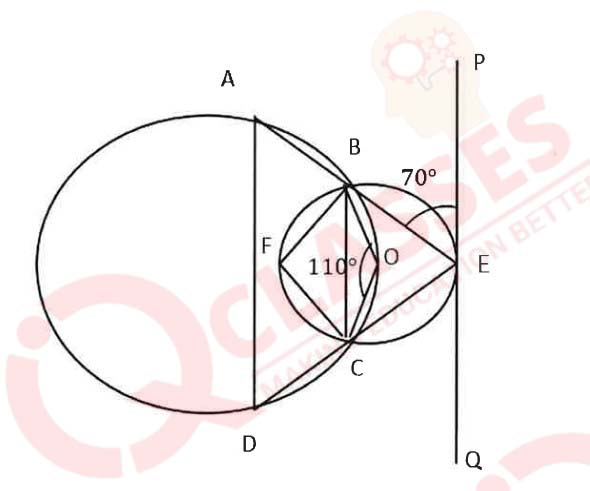
(a) ∠ECB,
(b) ∠BEC,
(c) ∠BFC,
(d) ∠DAB,

Solution

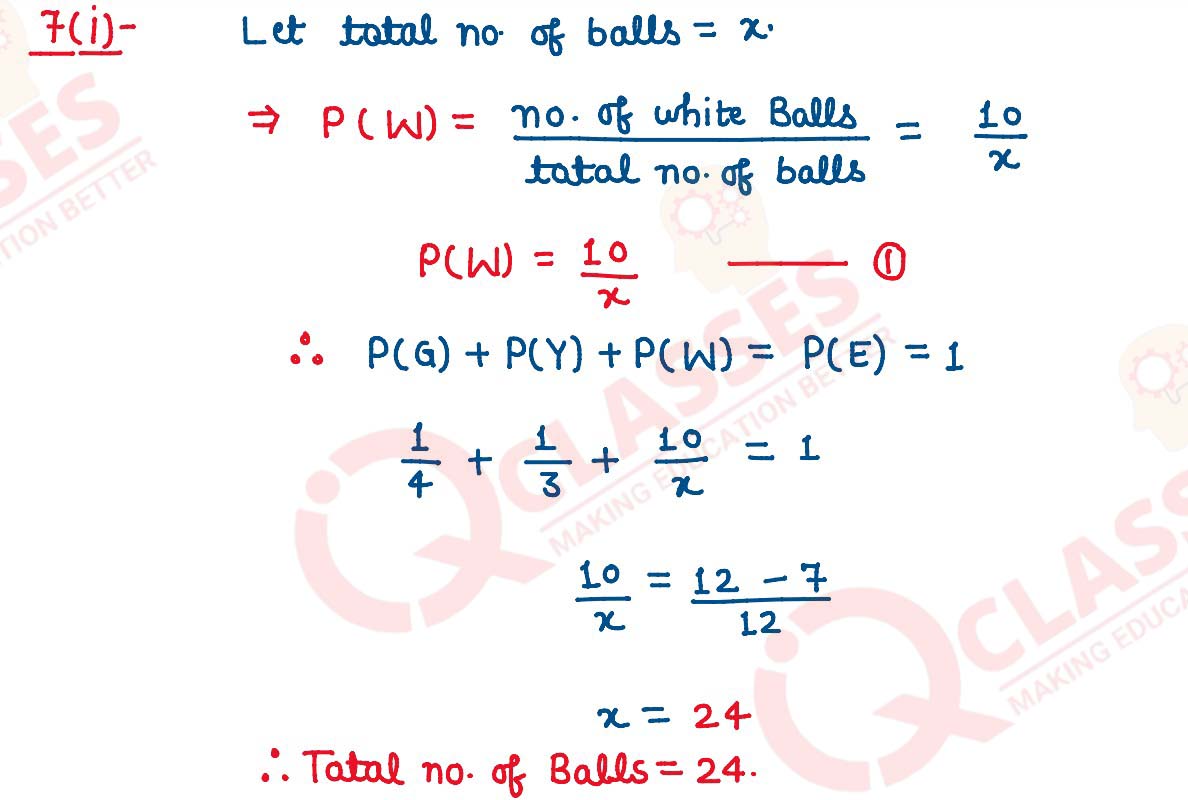
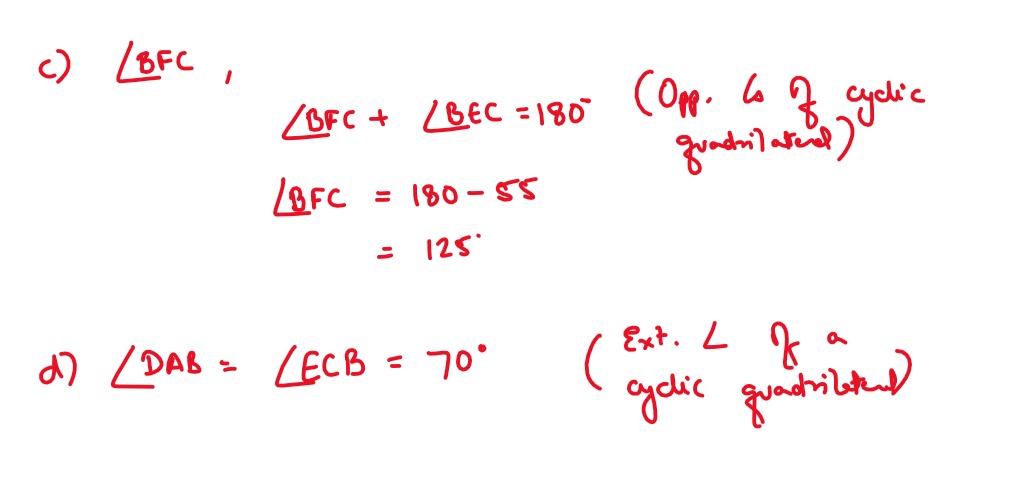
Question 8

(i) Solve the following inequation:

Represent the solution set on a number line.

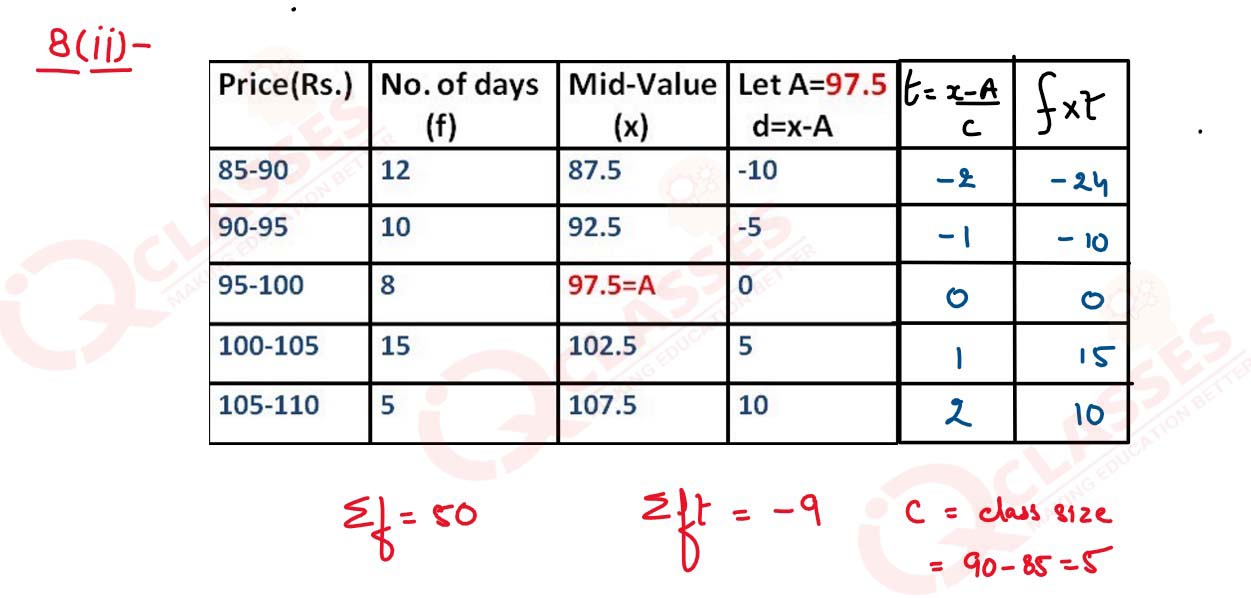
(ii) The following table gives the petrol prices per litre for a period of 50 days.

Find the mean price of petrol per litre to the nearest rupee using step — deviation method.

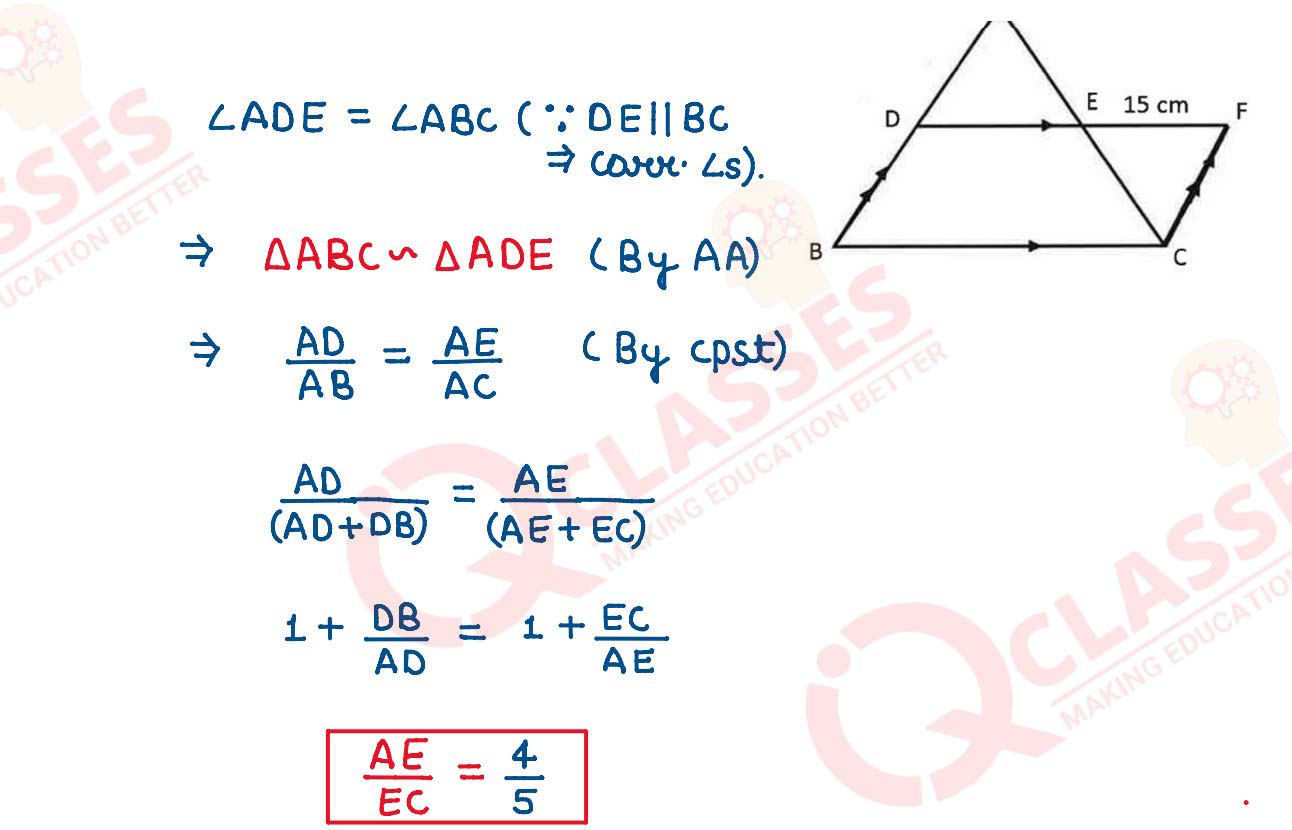
(iii) In the given diagram, ABC is a triangle and BCFD is a parallelogram. AD: DB = 4:5 and EF = 15 cm.

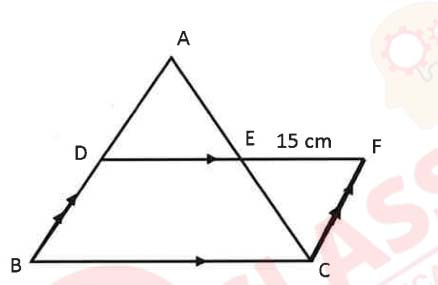
Find:
(a) AE:EC
(b) DE
(c) BC

Solution

Question 9

(i) Amit takes 12 days less than the days taken by Bijoy to complete a certain work. If both, working together, takes 8 days to complete the work, find the number of days taken by Bijoy to complete the work, working alone.

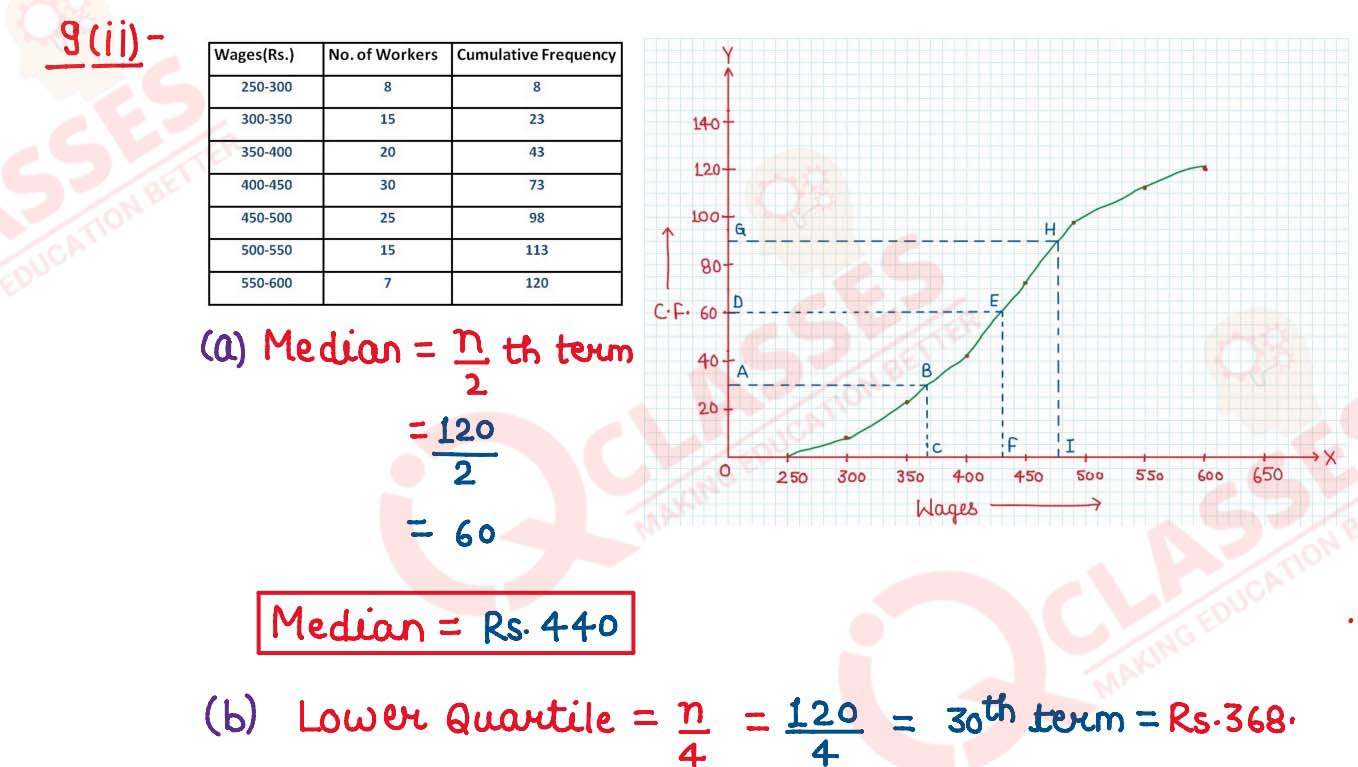
(ii) Use a graph sheet for this question. The daily wages of 120 workers working at a site are given below:

Use 2cm = Rs.50 and 2 cm = 20 workers along x - axis and y - axis respectively to draw an ogive and hence estimate:
(a) the median wages
(b) the inter - quartile range of wages
(c) percentage of workers whose daily wage is above Rs.475.

Solution

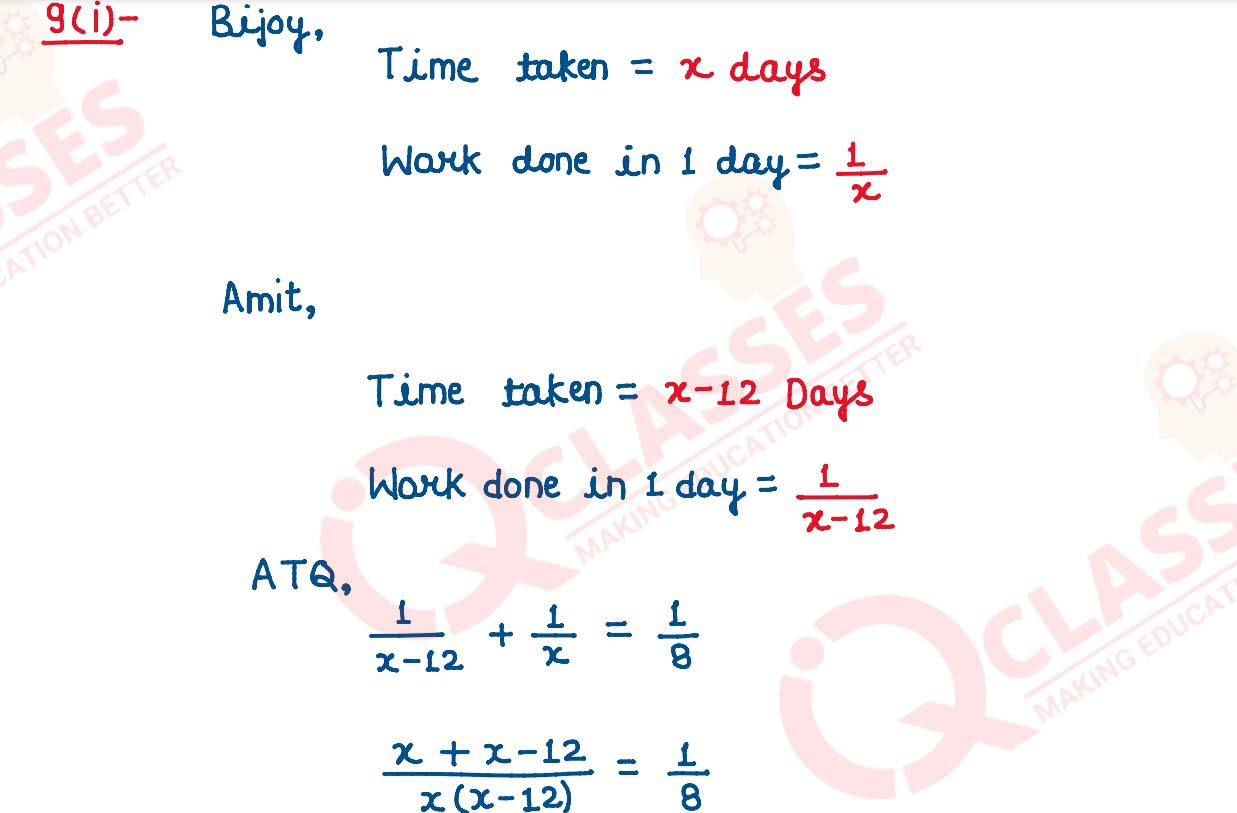
Question 10

(i) Solve for x, using the properties of proportion.

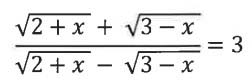
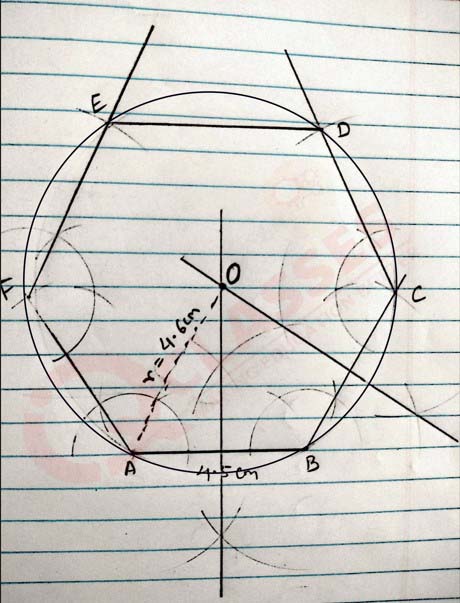
(ii) Using ruler and compasses, construct a regular hexagon of side 4.5 cm. Hence construct a circle circumscribing the hexagon. Measure and write down the length of the circum-radius.

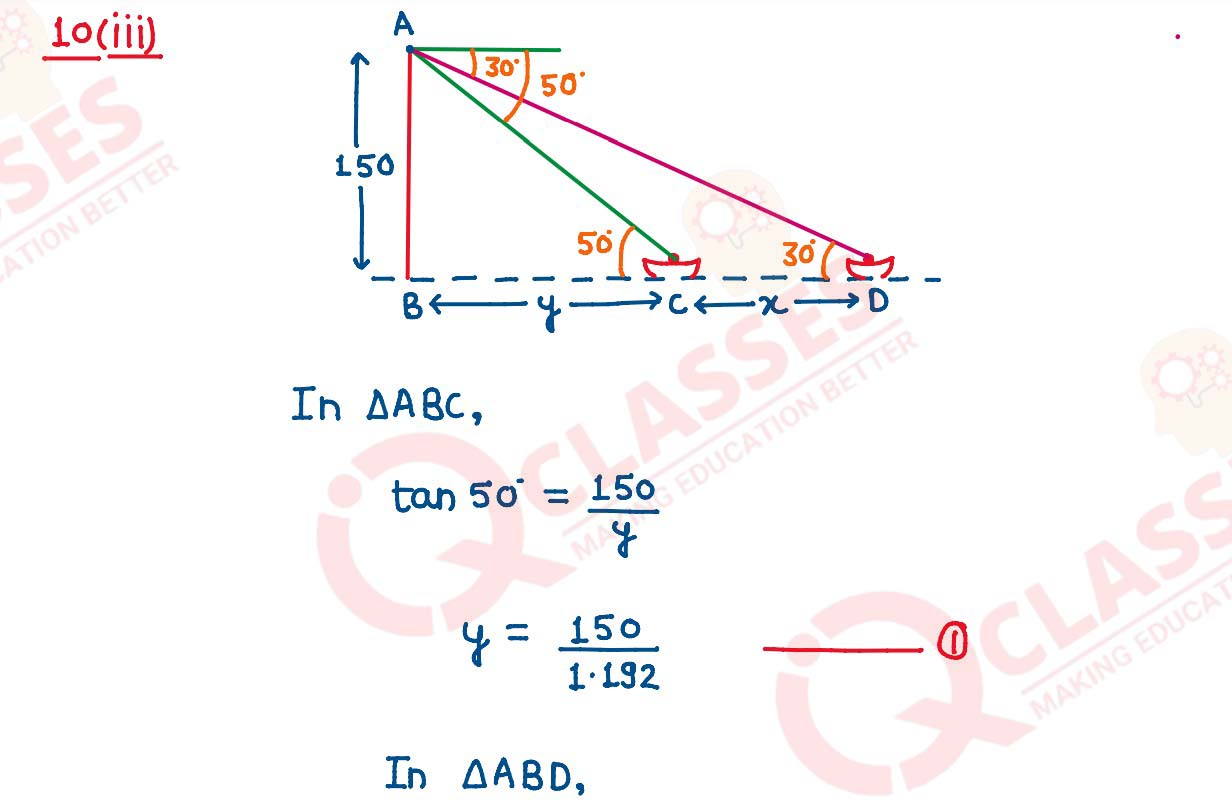
(iii) An observer standing on the top of a lighthouse 150 m above the sea level watches a ship sailing away. As he observes, the angle of depression of the ship changes from 50° to 30°. Determine the distance travelled by the ship during the period of observation. Give your answer correct to the nearest meter. (Use Mathematical Table for this question.)

Solution

(ii)