Class 12 CBSE Maths Specimen 2023
Maximum Marks: 80
Time Allowed: Three hours
This Question paper contains - five sections A, B, C, D and E. Each section is compulsory. However, there
are internal choices in some questions.
Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
Section C has 6 Short Answer (SA)-type questions of 3 marks each.
Section D has 4 Long Answer (LA)-type questions of 5 marks each.
Section E has 3 source based/case based/passage based/integrated units of
assessment (4 marks each) with sub parts.
class 12 CBSE Maths Specimen Question Paper 2023
SECTION A
Question 1
If A =[aij] is a skew-symmetric matrix of order n, then
- aij=1/aji ∀ 𝑖,
- aij ≠ 0 ∀ i,
- 𝑎ij = 0, 𝑤ℎ𝑒𝑟𝑒 𝑖 = j
- 𝑎ij ≠ 0 𝑤ℎ𝑒𝑟𝑒 𝑖 = j
Solution

If A is a square matrix of order 3, |𝐴′| = −3, then |𝐴𝐴′| =
- 9
- -9
- 3
- -3
Solution
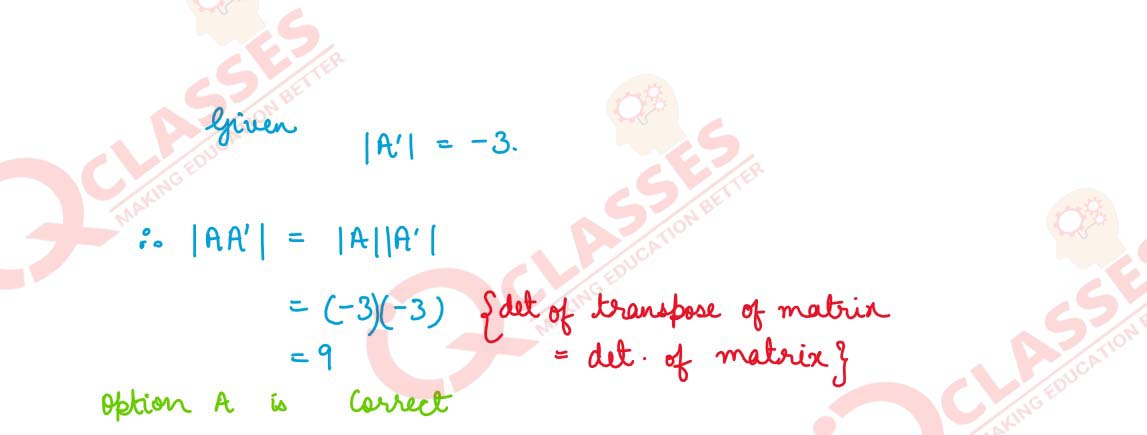
The area of a triangle with vertices A, B, C is given by
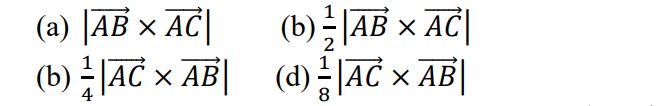
Solution

The value of ‘k’ for which the function
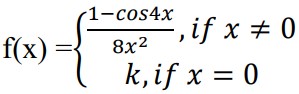
is continuous at x = 0 is
- 0
- -1
- 1
- 2
Solution

If f'(x)=x+ 1/x, then 𝑓(𝑥) is
- x2 + log |𝑥| + C
- x2/2+ log |x|+ C
- x/2 + log|x| + C
- x/2 -log|x| +C
Solution

If m and n, respectively, are the order and the degree of the differential equation
d
/
dx
[(
dy
/
dx
)]4
= 0, then m + n =
- 1
- 2
- 3
- 4
Solution

The solution set of the inequality 3x + 5y< 4 is
- an open half-plane not containing the origin.
- an open half-plane containing the origin.
- the whole XY-plane not containing the line 3x + 5y = 4.
- a closed half plane containing the origin.
Solution

The scalar projection of the vector 3𝚤̂− 𝚥̂− 2k^ 𝑜𝑛 𝑡ℎ𝑒 vector 𝚤̂ + 2𝚥̂−
3k^ is
- 7/√14
- 7/14
- 6/13
- 7/2
Solution

The value of ∫23
x
/
x2+1
dx is
- log 4
- log 3/2
- 1/2log 2
- log 9/4
Solution


If A, B are non-singular square matrices of the same order, then (𝐴𝐵-1)-1 =
- A-1B
- A-1B-1
- BA-1
- AB
Solution

The corner points of the shaded unbounded feasible region of an LPP are (0, 4),
(0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective
function Z = 4x + 6y occurs at
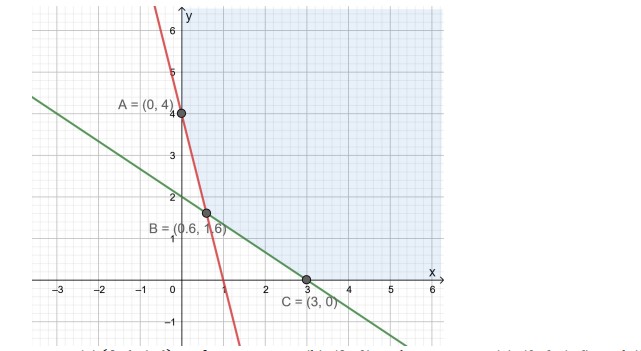
- (0.6, 1.6) 𝑜𝑛𝑙y
- (3, 0) only
- (0.6, 1.6) and (3, 0) only
- at every point of the line-segment joining the points (0.6, 1.6) and (3, 0)
Solution

If
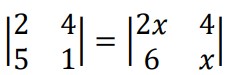
- 3
- √3
- -√3
- √3, −√3
Solution

If A is a square matrix of order 3 and |A| = 5, then |𝑎𝑑𝑗𝐴| =
- 5
- 25
- 125
- 1/5
Solution

Given two independent events A and B such that P(A) =0.3, P(B) =0.6 and P(𝐴' ∩ B') is
- 0.9
- 0.18
- 0.28
- 0.1
Solution

The general solution of the differential equation 𝑦𝑑𝑥 − 𝑥𝑑𝑦 = 0 𝑖s
- 𝑥𝑦 = 𝐶
- 𝑥 = 𝐶𝑦2
- 𝑦 = 𝐶x
- 𝑦 = 𝐶𝑥2
Solution
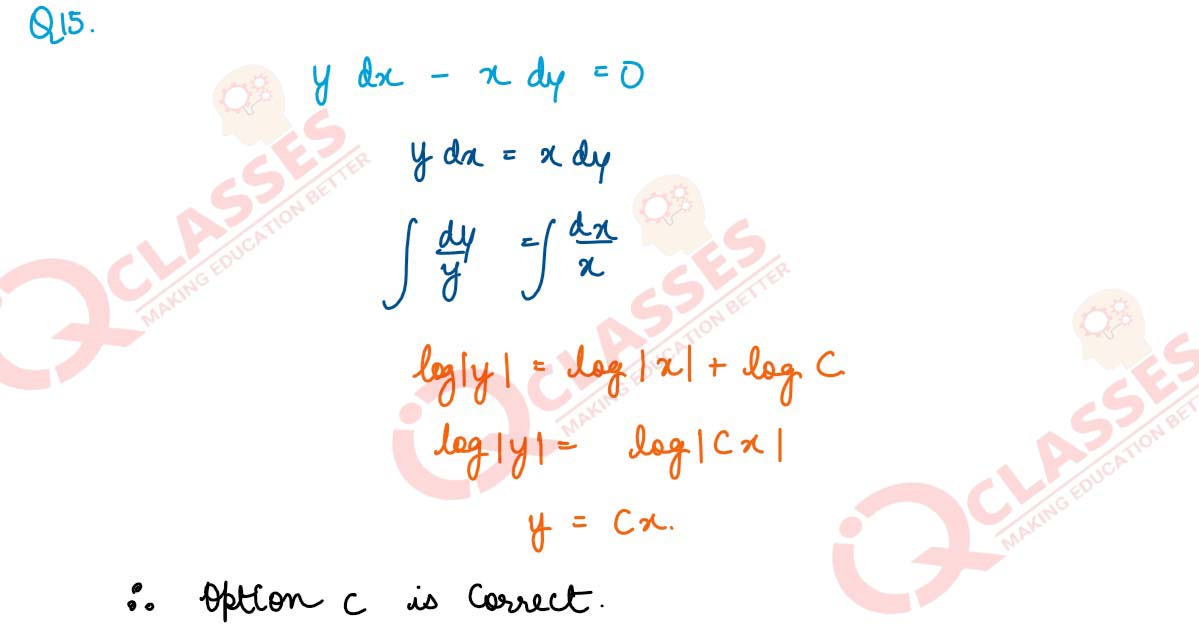
If 𝑦 = 𝑠𝑖𝑛-1𝑥, then (1 − 𝑥2)𝑦2 𝑖𝑠 equal to
- xy1
- xy
- xy2
- x2
Solution

If two vectors 𝑎⃗ 𝑎𝑛𝑑 b-> are such that |𝑎⃗|
=
2 ,|b->| = 3 and
a->.b->= 4,𝑡ℎ𝑒𝑛 |𝑎⃗ − 2𝑏->| is
equal to
- √2
- 2√6
- 24
- 2√2
Solution

P is a point on the line joining the points 𝐴(0,5, −2) and 𝐵(3, −1,2). If the x-coordinate
of P is 6, then its z-coordinate is
- 10
- 6
- -6
- -10
Solution


ASSERTION-REASON BASED QUESTIONS
In the following questions, a statement of assertion (A) is followed by a statement of
Reason (R). Choose the correct answer out of the following choices
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
Solution

Solution

SECTION B
Question 21
Find the value of sin-1[sin(
13π
/
7
)]
OR
Prove that the function f is surjective, where 𝑓: 𝑁 → 𝑁 such that
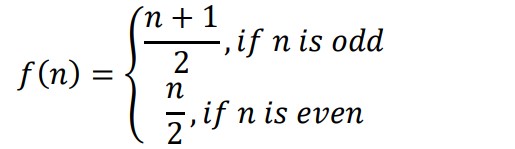
Is the function injective? Justify your answer
Solution

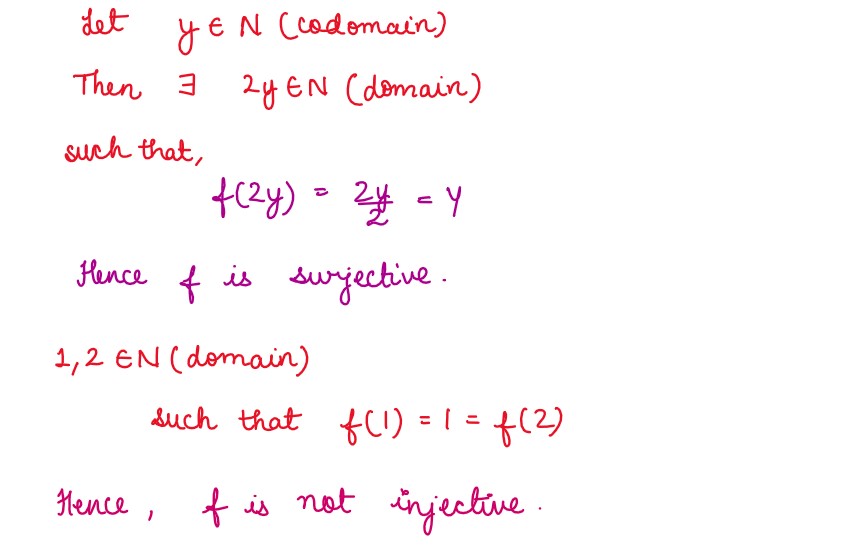
A man 1.6 m tall walks at the rate of 0.3 m/sec away from a street light that is 4 m above the ground. At what rate is the tip of his shadow moving? At what rate is his shadow lengthening?
Solution



If 𝑎⃗ = 𝚤̂− 𝚥̂+ 7k^ 𝑎𝑛𝑑 𝑏-> = 5𝚤̂− 𝚥̂+ 𝜆k^, then find the
value of 𝜆 so that the
vectors
a-> + 𝑏-> 𝑎𝑛𝑑 a-> - 𝑏-> are orthogonal
OR
Find the direction ratio and direction cosines of a line parallel to the line whose equations
are
6𝑥 − 12 = 3𝑦 + 9 = 2𝑧 − 2
Solution



If 𝑦√1 − 𝑥2 + 𝑥√1 − 𝑦2 = 1 ,𝑡ℎ𝑒𝑛 𝑝𝑟𝑜𝑣𝑒 𝑡ℎ𝑎𝑡
dy
/
dx
= -
√ 1-y2
/
√ 1-x2
Solution

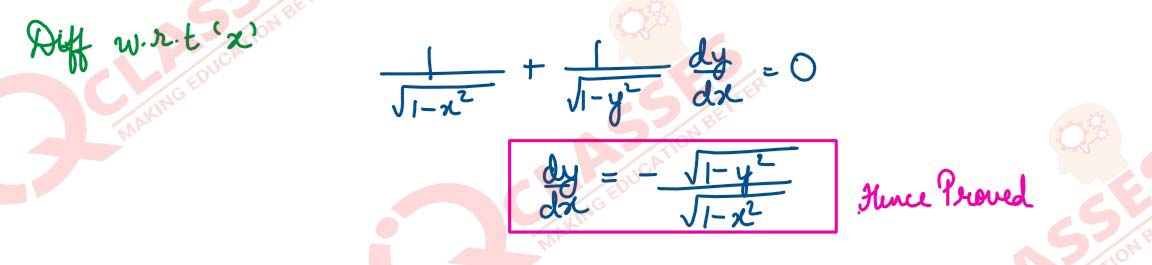
Find |𝑥⃗| if (𝑥⃗ − 𝑎⃗). (𝑥⃗ + 𝑎⃗) = 12, where 𝑎⃗ is a unit vector.
Solution

SECTION C
Question 26
Find: ∫
dx
/
√3-2x-x2
Solution

Three friends go for coffee. They decide who will pay the bill, by each tossing a coin and
then letting the “odd person” pay. There is no odd person if all three tosses produce the
same result. If there is no odd person in the first round, they make a second round of
tosses and they continue to do so until there is an odd person. What is the probability
that exactly three rounds of tosses are made?
OR
Find the mean number of defective items in a sample of two items drawn one-by-one
without replacement from an urn containing 6 items, which include 2 defective items.
Assume that the items are identical in shape and size.
Solution


Evaluate:
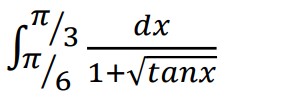
OR
Evaluate:
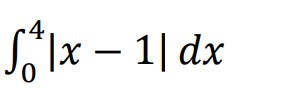
Solution


Solve the differential equation: 𝑦𝑑𝑥 + (𝑥 − 𝑦2)𝑑𝑦= 0
OR
Solve the differential equation: 𝑥𝑑𝑦 − 𝑦𝑑𝑥 = √ x2 + y2 dx
Solution



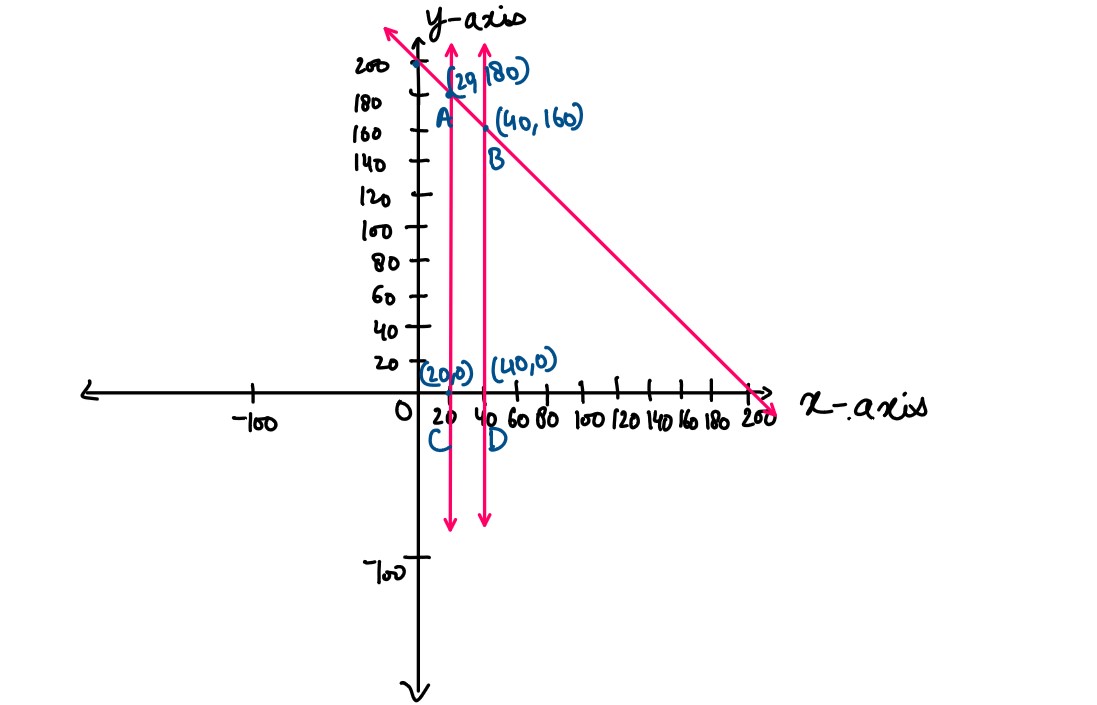
Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to 𝑥 + 𝑦 ≤ 200, 𝑥 ≤ 40, 𝑥 ≥ 20, 𝑦 ≥ 0
Solution

Find:
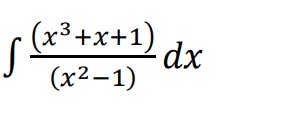
Solution


SECTION D
Question 32
Make a rough sketch of the region {(𝑥, 𝑦): 0 ≤ 𝑦 ≤ 𝑥2, 0 ≤ 𝑦 ≤ 𝑥, 0 ≤ 𝑥 ≤ 2} and find the area of the region using integration.
Solution


Define the relation R in the set 𝑁 × 𝑁 as follows:
For (a, b), (c, d) ∈ 𝑁 × 𝑁, (a, b) R (c, d) iff ad = bc. Prove that R is an equivalence
relation in 𝑁 × 𝑁.
OR
Given a non-empty set X, define the relation R in P(X) as follows:
For A, B ∈ 𝑃(𝑋), (𝐴, 𝐵) ∈
symmetric.
Solution



An insect is crawling along the line 𝑟̅ = 6𝚤̂ + 2𝚥̂ + 2𝑘^ + λ(𝚤̂ − 2𝚥̂ +
2𝑘^) and another insect is crawling along the line 𝑟̅ = −4𝚤̂ − 𝑘^ +
𝜇(3𝚤̂ − 2𝚥̂ − 2𝑘^). At what points on the lines should they reach so that the
distance between them is the shortest?Find the shortest possible distance between them.
OR
The equations of motion of a rocket are:
𝑥 = 2𝑡, 𝑦 = −4𝑡, 𝑧 = 4𝑡, where the time t is given in seconds, and the coordinates of a moving
point in km. What is the path of the rocket? At what distances will the rocket be from the starting
point O(0,0,0) and from the following line in 10 seconds?
𝑟⃗ = 20𝚤̂ − 10𝚥̂ + 40k^ + 𝜇(10𝚤̂ − 20𝚥̂ + 10𝑘^)
Solution






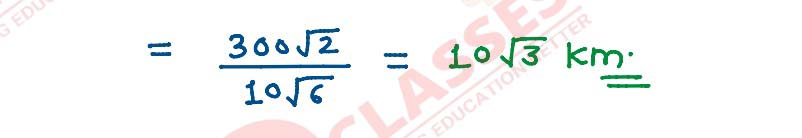
If
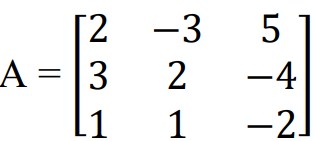 ,find 𝐴-1.
Use
𝐴-1 to solve the following system of equations
,find 𝐴-1.
Use
𝐴-1 to solve the following system of equations
2x-3y+5z=11,3x+2y − 4𝑧 = −5, 𝑥 + 𝑦 − 2𝑧 = −3
Solution


SECTION E
Question 36
Case-Study 1: Read the following passage and answer the questions given below.

The temperature of a person during an intestinal illness is given by
𝑓(𝑥) = −0.1𝑥2 + 𝑚𝑥 + 98
temperature in °F at x days
(i) Is the function differentiable in the interval (0, 12)? Justify your answer
(ii) If 6 is the critical point of the function,then find the value of the constant m
(iii)Find the intervals in which the function is strictly increasing/strictly decreasing
OR
Find the points of local maximum/local minimum, if any, in the interval (0, 12) as
well as the points of absolute maximum/absolute minimum in the interval [0, 12].
Also, find the corresponding local maximum/local minimum and the absolute
maximum/absolute minimum values of the function.
Solution





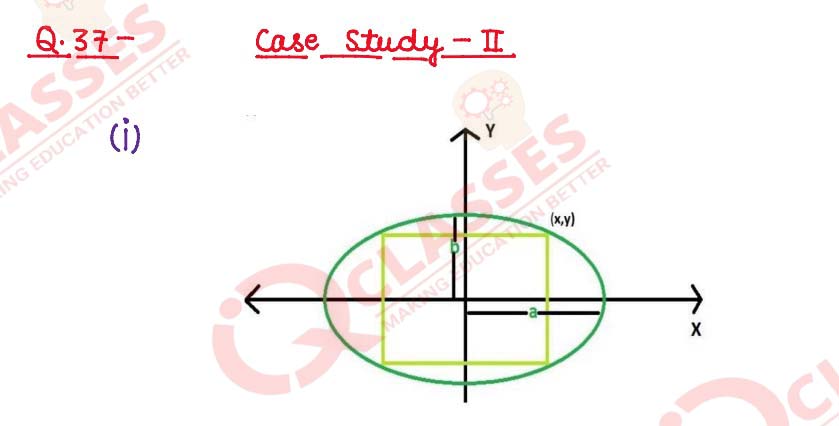
Case-Study 2: Read the following passage and answer the questions given below.

In an elliptical sport field the authority wants to design a rectangular soccer field
with the maximum possible area. The sport field is given by the graph of
x2
/
a2
+
y2
/
b2
=1
(i) If the length and the breadth of the rectangular field be 2x and 2y respectively,
then find the area function in terms of x.
(ii) Find the critical point of the function.
(iii) Use First derivative Test to find the length 2x and width 2y of the soccer field (in
terms of a and b) that maximize its area
OR
(iii) Use Second Derivative Test to find the length 2x and width 2y of the soccer field
(in terms of a and b) that maximize its area.
Solution




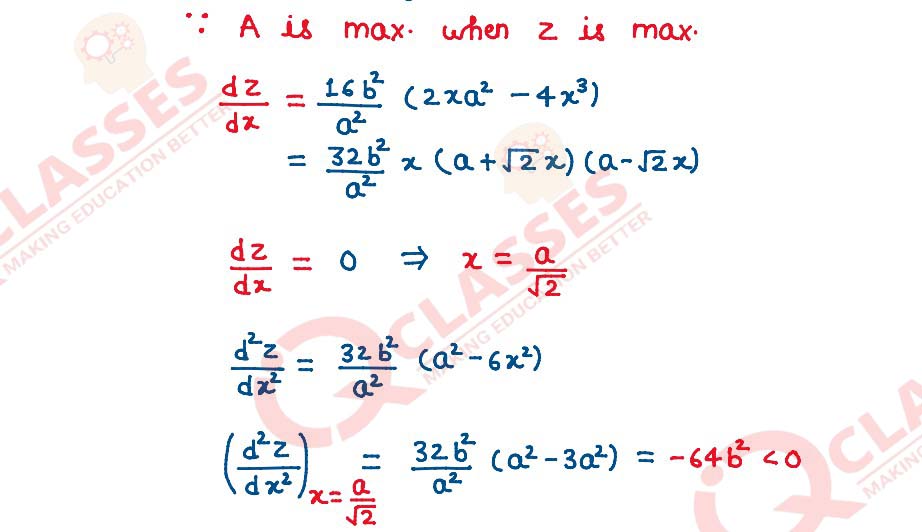

Case-Study 3: Read the following passage and answer the questions given below.

There are two antiaircraft guns, named as A and B. The probabilities that the shell fired
from them hits an airplane are 0.3 and 0.2 respectively. Both of them fired one shell at an
airplane at the same time
(i) What is the probability that the shell fired from exactly one of them hit the plane?
(ii) If it is known that the shell fired from exactly one of them hit the plane, then what is
the probability that it was fired from B?
Solution




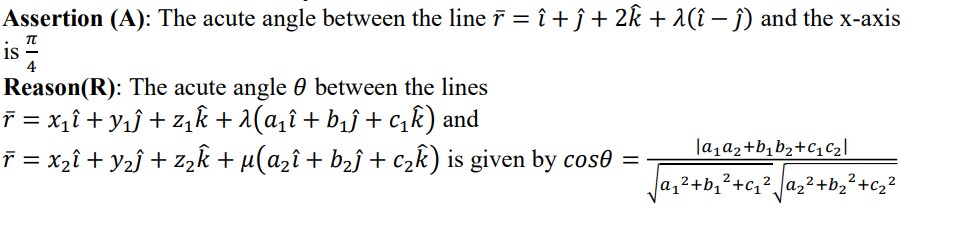
Add a comment