Class12 CBSE TERM1 MATHS SPECIMEN 2022

SECTION- A

Q.1 sin[^π⁄ ₃]- sin^-1 (-1/2)

1. 1/2
2. 1/3
3. -1
4. 1

Solution

Q.2 The value of k (k < 0) for which the function 𝑓 defined as

1. ±1
2. -1
3. ±1/2
4. 1/2

Solution

Q.3 If A = [aij] is a square matrix of order 2 such that
, then A² is:

Solution

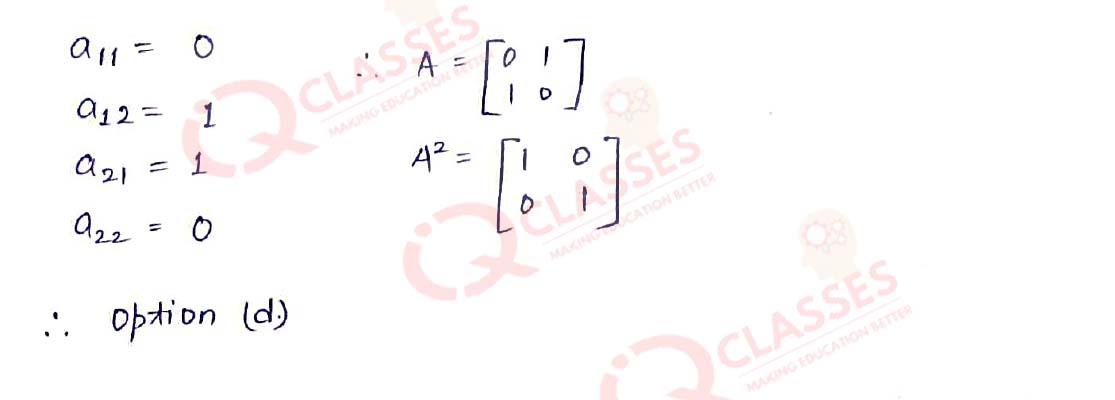
Q.4 Value of 𝑘, for which A =

k	8
4	2k

is a singular matrix is:

1. 4
2. -4
3. ±4
4. 0

Solution

Q.5 Find the intervals in which the function f given by f (x) = x² – 4x + 6 is strictly increasing:

1. (-∞,2) U (2, ∞)
2. (2, ∞)
3. (-∞,2)
4. (-∞,2]U (2, ∞)s

Solution

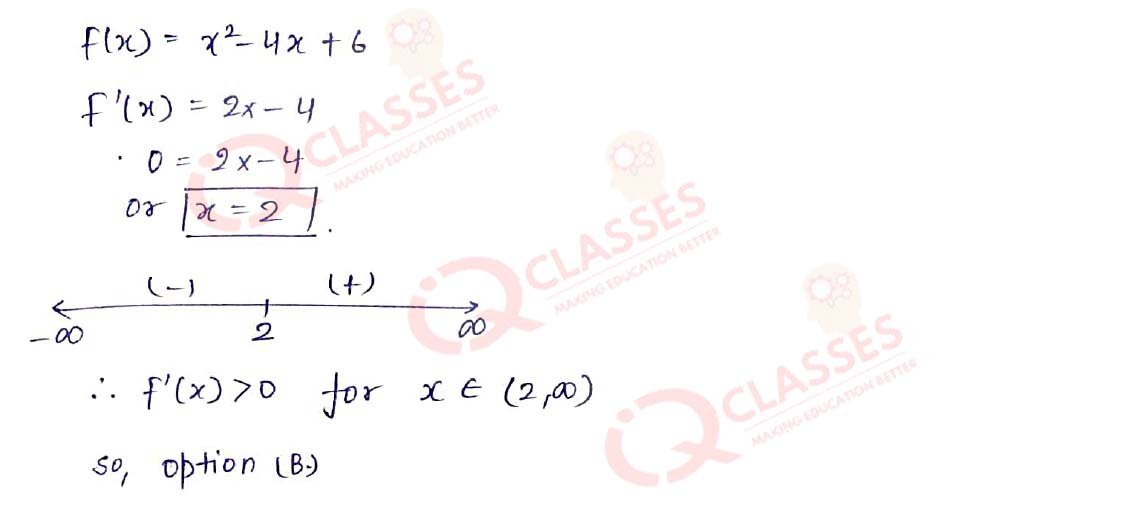
Q.6 Given that A is a square matrix of order 3 and | A | = - 4, then | adj A | is equal to:

1. -4
2. 4
3. -16
4. 16

Solution

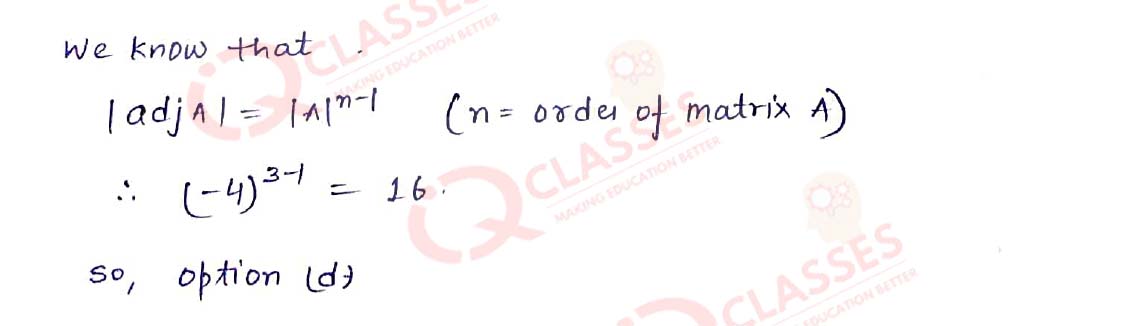
Q.7 A relation R in set A = {1,2,3} is defined as R = {(1, 1), (1, 2), (2, 2), (3, 3)}. Which of the following ordered pair in R shall be removed to make it an equivalence relation in A?

1. (1, 1)
2. (1, 2)
3. (2, 2)
4. (3, 3)

Solution

Q.8 If

2a+b	a-2b
5c-d	4c+3d

=

4	-3
11	24

, then value of a + b - c + 2d is:

1. 8
2. 10
3. 4
4. -8

Solution

Q.9 The point at which the normal to the curve y = 𝑥 + 1/x, x > 0 is perpendicular to the line 3x – 4y – 7 = 0 is:

1. (2, 5/2)
2. (±2, 5/2)
3. (- 1/2, 5/2
4. (1/2, 5/2)

Solution

Q.10 sin (tan^-1x), where |x| < 1, is equal to:

1. ^x ⁄ _{√ 1-x²}
2. ¹ ⁄ _{√ 1-x²}
3. ¹ ⁄ _{√ 1+x²}
4. ^x ⁄ _{√ 1+x²}

Solution

Q.11 Let the relation R in the set A = {x ∈ Z : 0 ≤ x ≤ 12}, given by R = {(a, b) : |a –b| is a multiple of 4}. Then [1], the equivalence class containing 1, is:

1. {1, 5, 9}
2. {0, 1, 2, 5}
3. ∅
4. A

Solution

Q.12 If e^x + e^y = e^x+y , then 𝑑𝑦/𝑑𝑥 is:

1. e ^{y - x}
2. e^x+y
3. - e ^{y - x}
4. 2e ^{x - y}

Solution

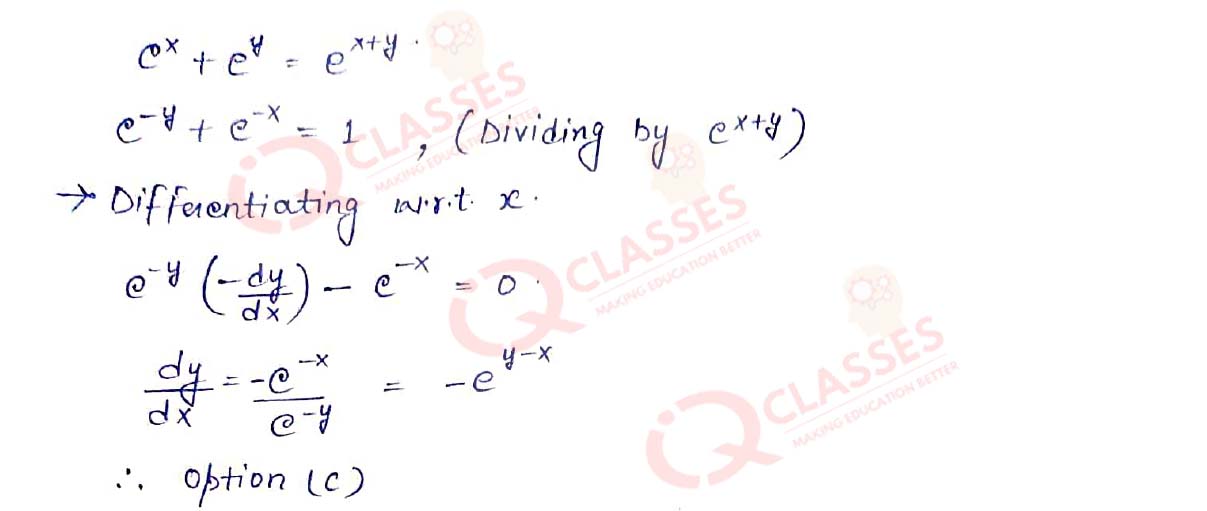
Q.13 Given that matrices A and B are of order 3×n and m×5 respectively, then the order of matrix C = 5A +3B is:

1. 3×5
2. ₹5×3
3. 3×3
4. 5×5

Solution

Q.14 If y = 5 cos x – 3 sin x, then 𝑑²𝑦 ⁄ 𝑑𝑥²is equal to:

1. -y
2. y
3. 25y
4. 9y

Solution

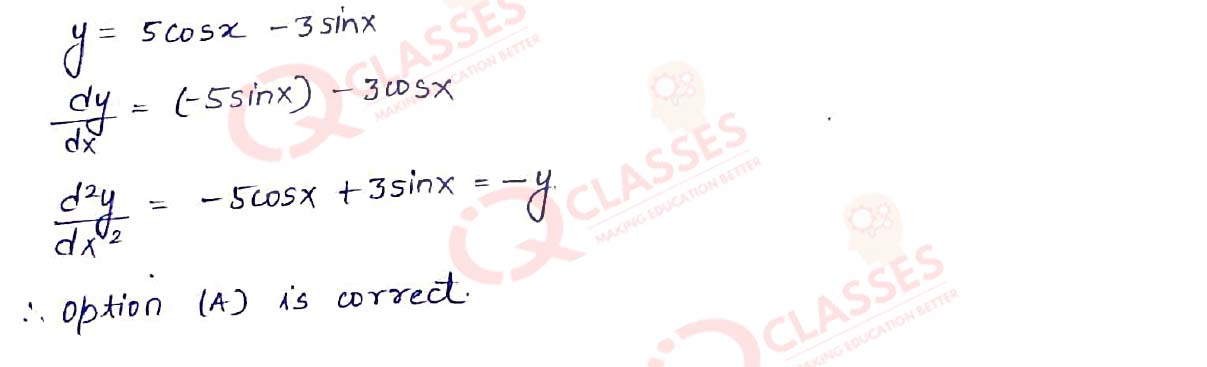
Q.15 For matrix A =

2	5
-11	7

, (adj A)' is equal to:

1. 2	-5
   11	-7

2. 7	5
   11	2

3. 7	11
   -5	2

4. 7	-5
   11	2

Solution

Q.16 The points on the curve ^𝑥2⁄₉ + ^y2⁄₁₆ = 1 at which the tangents are parallel to y axis are:

1. (0,±4 )
2. (±4,0)
3. (±3,0)
4. (0, ±3)

Solution

Q.17 Given that A = [𝑎𝑖𝑗] is a square matrix of order 3×3 and |A| = −7, then the value of ∑³_i=1 𝑎_𝑖2𝐴_𝑖2, where 𝐴𝑖𝑗 denotes the cofactor of element 𝑎_𝑖𝑗 is:

1. 7
2. -7
3. 0
4. 49

Solution

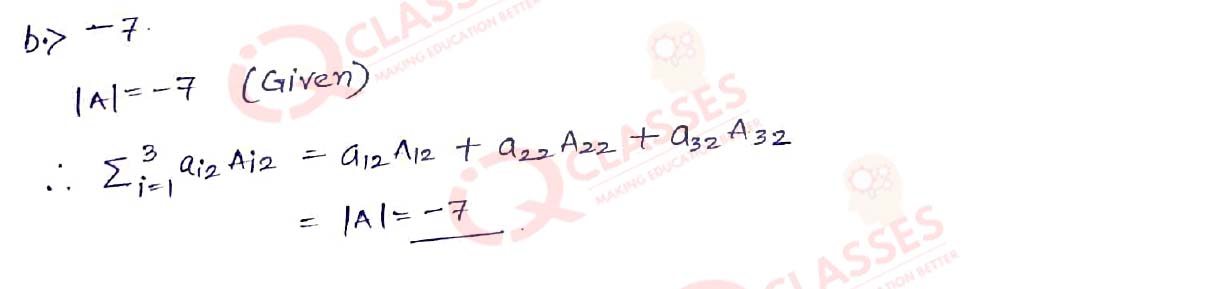
Q.18 If y = log(cos 𝑒^𝑥), then 𝑑𝑦/𝑑𝑥is:

1. cos𝑒^𝑥−1
2. e^-xcos e ^x
3. e^x sin e^x
4. -e^x tan e^x

Solution

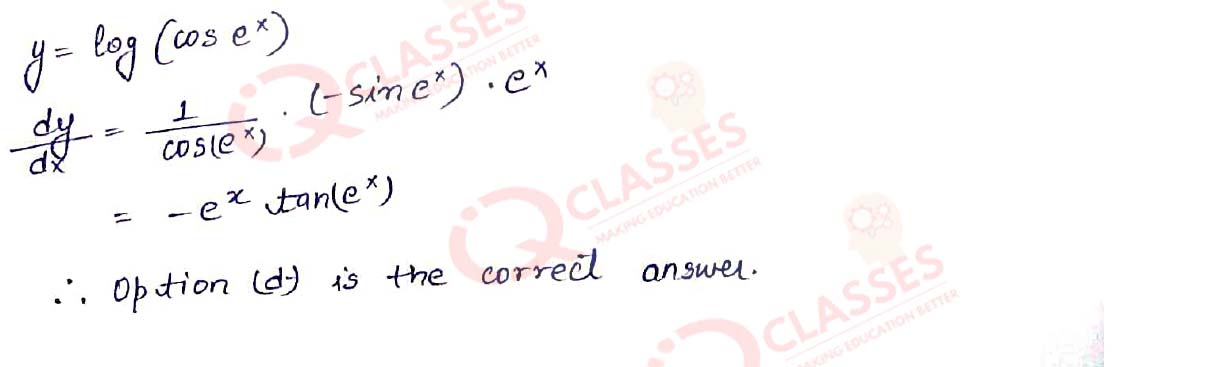
Q.19 Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?

1. Point B
2. Point C
3. Point D
4. every point on the line segment CD

Solution

Q.20 The least value of the function 𝑓(𝑥) = 2𝑐𝑜𝑠𝑥 + 𝑥 in the closed interval [0,𝜋/2] is:

1. 2
2. ^𝜋⁄₆ + √3
3. 𝜋/2
4. The least value does not exist

Solution

Q.21 The function 𝑓: R⟶R defined as 𝑓(𝑥) = 𝑥³ is:

1. One-on but not onto
2. Not one-one but onto
3. Neither one-one nor onto
4. One-one and onto

Solution

Q.22 If x = a sec 𝜃, y = b tan 𝜃, then ^𝑑2𝑦 ⁄ _𝑑𝑥² at 𝜃 =𝜋/6 is:

1. ^−3√3𝑏⁄ _𝑎²
2. ^−2√3𝑏⁄ _𝑎
3. ^−3√3𝑏⁄ _𝑎
4. ^-b⁄ _3√3𝑎²

Solution

Q.23 In the given graph, the feasible region for a LPP is shaded. The objective function Z = 2x – 3y, will be minimum at:

1. (4, 10)
2. (6, 8)
3. (0, 8)
4. (6, 5)

Solution

Q.24 The derivative of sin^-1 (2𝑥√ 1 − 𝑥²) w.r.t sin^-1x, −1/√2 < 𝑥 < 1/√2, is:

1. 2
2. (𝜋/2)-2
3. 𝜋/2
4. −2

Solution

SECTION- B

Q.25 If A =

1	-1	0
2	3	4
0	1	2

and B =

2	2	-4
-4	2	-4
2	-1	5

, then:

1. A^-1 = B
2. A^-1 = 6B
3. B^-1 = B
4. A^-1 = 1/6 A

Solution

Q.26 The real function f(x) = 2x³ – 3x² – 36x + 7 is:

1. Strictly increasing in (−∞, −2) and strictly decreasing in ( −2, ∞)
2. Strictly decreasing in ( −2, 3)
3. Strictly decreasing in (−∞, 3) and strictly increasing in (3, ∞)
4. Strictly decreasing in (−∞, −2) ∪ (3, ∞)

Solution

Q.27 Simplest form of tan^-1
, 𝜋 < 𝑥 < ^3𝜋⁄₂ is:

1. ₹20 Per share
2. ₹18 Per share
3. ₹22 Per share
4. ₹8 Per share

Solution

Q.28 Given that A is a non-singular matrix of order 3 such that A2 = 2A, then value of |2A| is:

1. 4
2. 8
3. 64
4. 16

Solution

Q.29 The value of 𝑏 for which the function 𝑓(𝑥) = 𝑥 + 𝑐𝑜𝑠𝑥 + 𝑏 is strictly decreasing over R is:

1. 𝑏 < 1
2. No value of b exists
3. 𝑏 ≤ 1
4. 𝑏 ≥ 1

Solution

Q30. Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}, then

1. (2,4) ∈ R
2. (3,8) ∈ R
3. (6,8) ∈ R
4. (8,7) ∈ R

Solution

Q.31 The point(s), at which the function f given by
is continuous, is/are:

1. 𝑥 𝜖 R
2. 𝑥 = 0
3. 𝑥 𝜖 R –{0}
4. 𝑥 = −1 and 1

Solution

Q.32 If A =

0	2
3	-4

and 𝑘A =

0	3a
2b	24

, then the values of 𝑘, 𝑎 and 𝑏 respectively are:

1. −6, −12, −18
2. −6, −4, −9
3. 6, 4, 9
4. −6, 12, 18

Solution

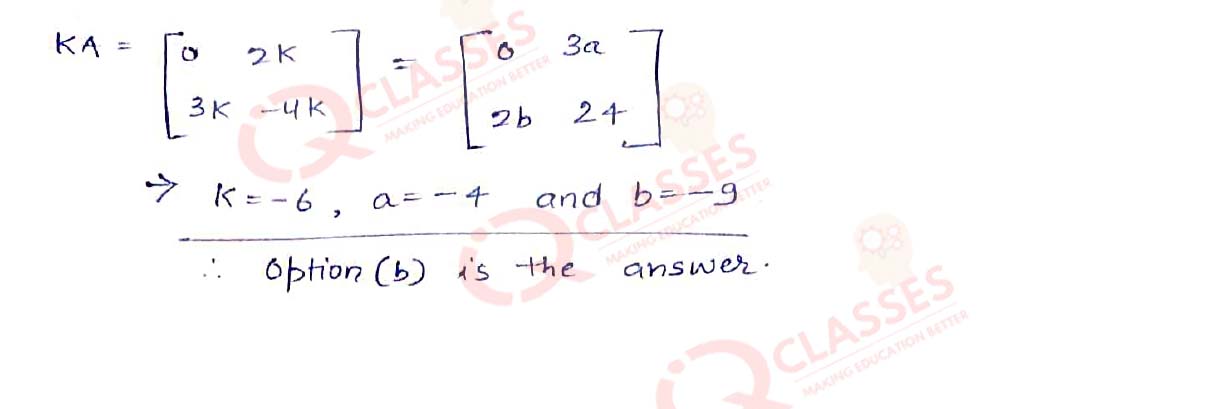
Q.33 A linear programming problem is as follows:
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 𝑍 = 30𝑥 + 50𝑦
subject to the constraints,
3𝑥 + 5𝑦 ≥ 15
2𝑥 + 3𝑦 ≤ 18
𝑥 ≥ 0, 𝑦 ≥ 0
In the feasible region, the minimum value of Z occurs at

1. a unique point
2. no point
3. infinitely many points
4. two points only

Solution

Q.34 The area of a trapezium is defined by function 𝑓 and given by 𝑓(𝑥) = (10 + 𝑥)√ 100 − 𝑥² , then the area when it is maximised is:

1. ₹75𝑐𝑚²
2. 7√3𝑐𝑚²
3. 75√3𝑐𝑚²
4. 5𝑐𝑚²

Solution

Q.35 If A is square matrix such that A2 = A, then (I + A)³ – 7 A is equal to:

1. A
2. I + A
3. I − A
4. I

Solution

Q.36 If tan^-1 x = y, then:

1. −1 < y < 1
2. −𝜋/2 ≤ y ≤ 𝜋/2
3. −𝜋/2 < y < 𝜋/2
4. y 𝜖{−𝜋/2,𝜋/2}

Solution

Q.37 Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let 𝑓 = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Based on the given information, 𝑓 is best defined as:

1. Surjective function
2. Injective function
3. Bijective function
4. function

Solution

Q.38 For A =

3	1
-1	2

, then 14A^-1 is given by:

1. 14

   2	-1
   1	3

2. 5

   4	-2
   2	6

3. 2

   2	-1
   1	−3

4. 2

   -3	-1
   1	−2

Solution

Q.39 The point(s) on the curve y = x³ – 11x + 5 at which the tangent is y = x – 11 is/are:

1. (-2,19)
2. (2, - 9)
3. (±2, 19)
4. (-2, 19) and (2, -9)

Solution

Q.40 Given that A =

𝛼	𝛽
𝛾	−𝛼

and A² = 3I, then:

1. 1 + 𝛼² + 𝛽𝛾 = 0
2. 1 - 𝛼² - 𝛽𝛾 = 0
3. 3 - 𝛼² - 𝛽𝛾 = 0
4. 3 + 𝛼² + 𝛽𝛾 = 0

Solution

Q.41 For an objective function 𝑍 = 𝑎𝑥 + 𝑏𝑦, where 𝑎, 𝑏 > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:

1. 𝑏 − 3𝑎 = 0
2. 𝑎 = 3b
3. 𝑎 + 2𝑏 = 0
4. 2𝑎 − 𝑏 = 0

Solution

Q.42 For which value of m is the line y = mx + 1 a tangent to the curve y² = 4x?

1. 1/2
2. 1
3. 2
4. 3

Solution

Q.43 The maximum value of [𝑥(𝑥 − 1) + 1]^1/3, 0 ≤ 𝑥 ≤ 1 is:

1. 0
2. 1/2
3. 1
4. 

Solution

Q.44 In a linear programming problem, the constraints on the decision variables x and y are 𝑥 − 3𝑦 ≥ 0, 𝑦 ≥ 0, 0 ≤ 𝑥 ≤ 3. The feasible region

1. is not in the first quadrant
2. is bounded in the first quadrant
3. is unbounded in the first quadrant
4. does not exist

Solution

Q.45 Let A =

1	sinα	1
-sinα	1	sinα
1	sinα	1

where 0 ≤ α ≤ 2π, then:

1. |A|=0
2. |A| 𝜖 (2, ∞)
3. |A| 𝜖 (2,4)
4. |A| 𝜖 [2,4]

Solution

CASE STUDY The fuel cost per hour for running a train is proportional to the square of the speed it generates in km per hour. If the fuel costs ₹ 48 per hour at speed 16 km per hour and the fixed charges to run the train amount to ₹ 1200 per hour.

Assume the speed of the train as 𝑣 km/h.Based on the given information, answer the following questions.

Q.46 Given that the fuel cost per hour is 𝑘 times the square of the speed the train generates in km/h, the value of 𝑘 is:

1. 16/3
2. 1/3
3. 3
4. 3/16

Solution

Q.47 If the train has travelled a distance of 500km, then the total cost of running the train is given by function:

Solution

Q.48 The most economical speed to run the train is:

1. 18km/h
2. 5km/h
3. 80km/h
4. 40km/h

Solution

Q.49 The fuel cost for the train to travel 500km at the most economical speed is:

1. ₹ 3750
2. ₹ 750
3. ₹ 7500
4. ₹ 75000

Solution

Q.50The total cost of the train to travel 500km at the most economical speed is:

1. ₹ 3750
2. ₹ 75000
3. ₹ 7500
4. ₹ 15000

Solution