Class 12 ISC Maths Specimen 2023
Maximum Marks: 80
Time Allowed: Three hours
(Candidates are allowed additional 15 minutes for only reading the paper.)
(They must NOT start writing during this time).
This Question Paper consists of three sections A, B and C.
Candidates are required to attempt all questions from Section A and all questions
EITHER from Section B OR Section C.
Section A: Internal choice has been provided in two questions of two marks each,
two questions of four marks each and two questions of six marks each.
Section B: Internal choice has been provided in one question of two marks and
one question of four marks.
Section C: Internal choice has been provided in one question of two marks and
one question of four marks.
All working, including rough work, should be done on the same sheet as,
and adjacent to the rest of the answer.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables and graph papers are provided.
SECTION A
Question 1
In subparts (i) to (x) choose the correct options and in subparts (xi) to (xv), answer the questions as instructed.
(i)
Which of the following is NOT an equivalence relation on Z?
- 𝑎𝑅𝑏 ⇔ 𝑎 + 𝑏 𝑖𝑠 𝑎𝑛 𝑒𝑣𝑒𝑛 𝑖𝑛𝑡𝑒𝑔𝑒r
- 𝑎𝑅𝑏 ⇔ 𝑎 − 𝑏 𝑖𝑠 𝑎𝑛 𝑒𝑣𝑒𝑛 𝑖𝑛𝑡𝑒𝑔𝑒r
- 𝑎𝑅𝑏 ⇔ 𝑎 < b
- 𝑎𝑅𝑏 ⇔ 𝑎 = b
Solution
.jpg)
(ii)
Let A be the set of all 50 cards numbered from 1 to 50. Let 𝑓: 𝐴 → 𝑁 be a function
defined by 𝑓(𝑥) = card number of the card ‘𝑥’. Then the function ‘𝑓’ is:
- one to one but not onto.
- onto but not one to one.
- neither one to one nor onto
- one to one and onto.
Solution
.jpg)
(iii)
The value of tan−1 √3 − sec-1 (−2) is equal to
-
π
/
3
-
2π
/
3
-
- π
/
3
-
π
/
4
Solution
.jpg)
(iv)
If
.jpg)
-1.jpg)
Solution
.jpg)
(v)
If 𝐴 is a 3 × 3 matrix such that
.jpg)
then the value of |AT| will be
- 27
- 9
- 3
- -3
Solution
.jpg)
(vi)
If
.jpg) , then
the value of |𝐵| is equal to
, then
the value of |𝐵| is equal to
- 𝑎 + 2𝑏 + 3c
- 𝑎 − 𝑏 + 2c
- 0
- 3a
Solution
.jpg)
(vii)
If sin-1 𝑥 + sin-1 𝑦 =
π
/
2
, then
dy
/
dx
is equal to
-
x
/
y
-
-
x
/
y
-
y
/
x
-
-
y
/
x
Solution
.jpg)
(viii)
If f(x)=
4-x2
/
4x-x3
then the function is:
- discontinuous at only one point
- discontinuous at exactly two points.
- discontinuous at exactly three points
- discontinuous at exactly four points
Solution
.jpg)
(ix)
The degree of the differential equation
.jpg) is
is
- 2
- 1
- 3
- not defined
Solution
.jpg)
(x)
If A and B are two events such that 𝑃(𝐴) > 0 and 𝑃(𝐵) ≠ 1 , then P (𝐴̅/𝐵̅) is
- 1 − 𝑃 (𝐴̅/𝐵 )
- 1 − 𝑃(𝐴/𝐵)
-
1 − P(𝐴 ∪ 𝐵)
/
𝑃(𝐵̅)
-
𝑃(𝐴̅)
/
𝑃(𝐵)
Solution
.jpg)
(xi) Write the smallest equivalence relation on the set 𝐴 = {𝑎, 𝑏, 𝑐}
Solution
.jpg)
(xii)
If
3
5
7
9
=X+Y,
where 𝑋 is skew- symmetric matrix and 𝑌 is symmetric
matrix. Find |𝑋|.
| 3 | 5 |
| 7 | 9 |
Solution
.jpg)
-1.jpg)
(xiii) If ∫ log 2𝑥 𝑑𝑥 = 𝑥log2𝑥 − 𝑘 + 𝑐 where 𝑘 is a function of 𝑥, then find k
Solution
.jpg)
(xiv) 50 tickets in a box are numbered 00, 01, 02 , .. .. , 49. One ticket is drawn randomly from the box. Find the probability of the ticket having the product of its digits 7, given that the sum of the digits is 8?
Solution
.jpg)
(xv) A speaks truth in 60% of cases and B speaks truth in 90% of the cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
Solution
.jpg)
(a) If 𝑦 = √sin 𝑥 + 𝑦 , then find
dy
/
dx
OR
(b) Find the point on the curve y2 = 4𝑥 + 8 for which the abscissa and ordinate changes
at the same rate
Solution



Let 𝑓: 𝑅 → 𝑅 defined as 𝑓(𝑥) = 2𝑥 − 3. Find
(i) 𝑓-1(𝑥)
(ii) domain and range of 𝑓-1(𝑥)
Solution


The function 𝑓 is defined for all x ∈ R . The line with equation 𝑦 = 6𝑥 − 1 is the tangent
to the graph of 𝑓 at 𝑥 = 4
(i) Write down the value of 𝑓′(4).
(ii) Find 𝑓(4).
Solution

Evaluate: ∫[sin(log 𝑥) + cos(log 𝑥)] 𝑑x
OR
Evaluate:
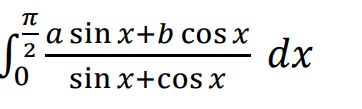
Solution



Solve the differential equation: (1 + 𝑦2)(1 + log 𝑥)𝑑𝑥 + 𝑥𝑑𝑦 = 0
Solution
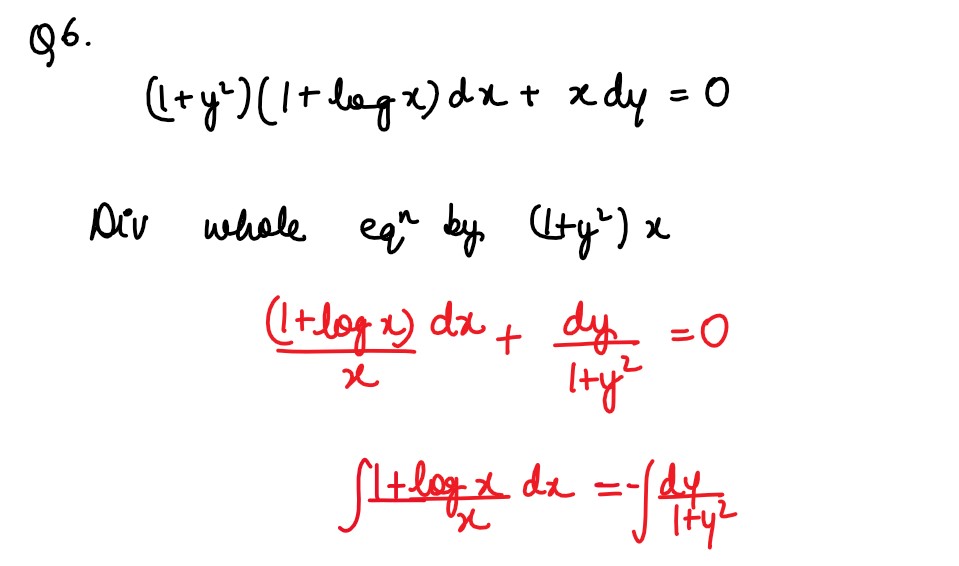
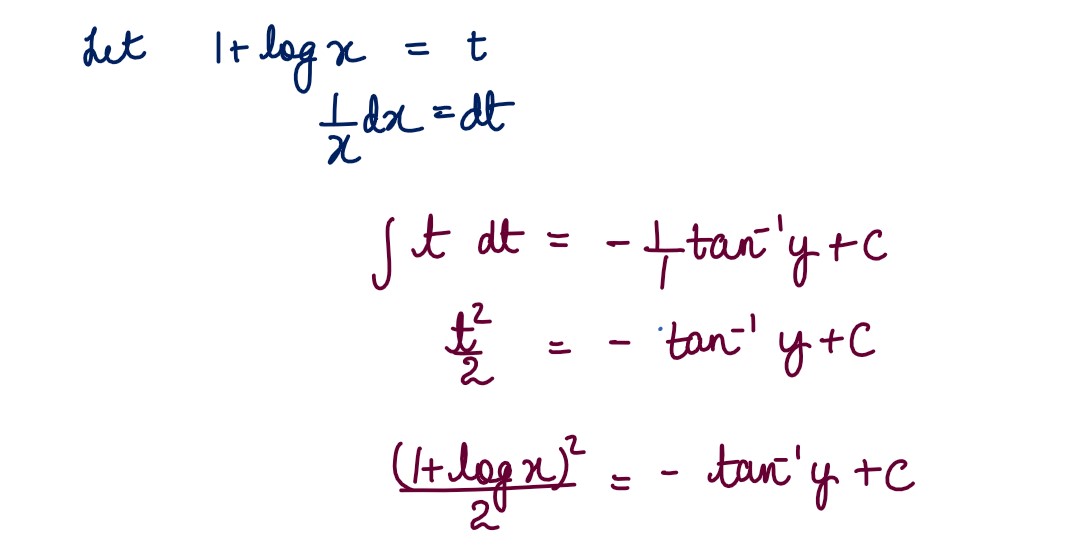
Solution


If y=(x+√1+x2)n,then prove that
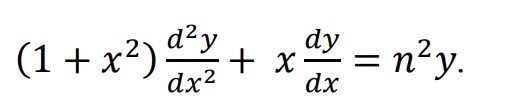
Solution


Evaluate :
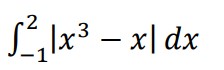
OR
Evaluate: ∫ √cosec 𝑥 − 1 𝑑x
Solution



(i) A student answers a multiple choice question with 5 alternatives, of which exactly
one is correct. The probability that he knows the correct answer is 1/5. If he does not
know the correct answer, he randomly ticks one answer. Given that he has answered
the question correctly, find the probability that he did not tick the answer randomly.
(ii) A candidate takes three tests in succession and the probability of passing the first test
is 1/2
. The probability of passing each succeeding test is 1/2 or 1/4
depending on whether
he passes or fails in the preceding one. The candidate is selected, if he passes at least
two tests. Find the probability that the candidate is selected.
Solution


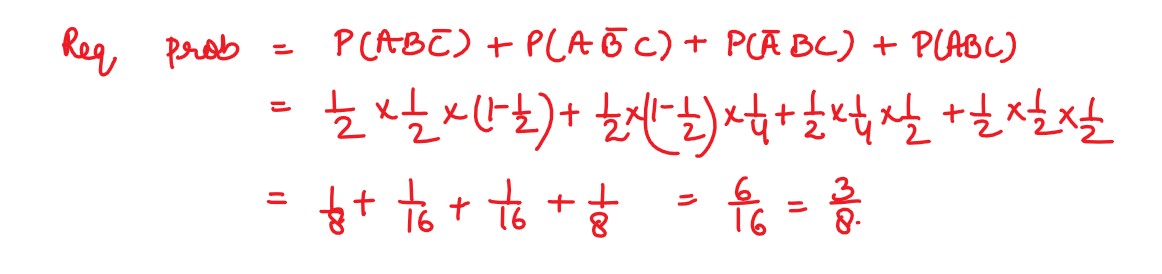
Find 𝐴-1, if
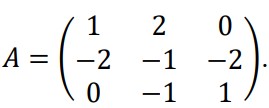
Using 𝐴-1, solve the system of linear equations:
x-2𝑦 = 10, 2𝑥 − 𝑦 − 𝑧 = 8, −2𝑦 + 𝑧 = 7
Solution

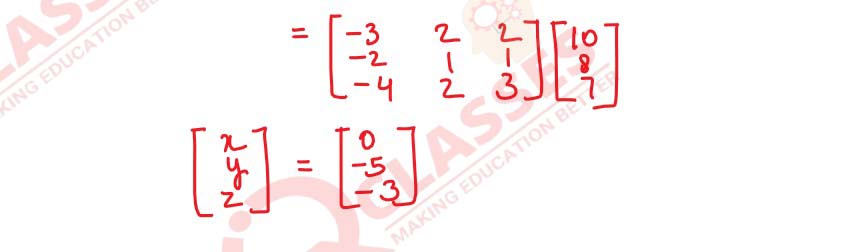
(i) Find the particular solution of the differential equation given below
(1 + 𝑥2)𝑑𝑦 = (tan-1 𝑥 − 𝑦)𝑑𝑥, given that 𝑦 = 1 𝑤ℎ𝑒𝑛 𝑥 = 0
OR
Evaluate: ∫
1
/
sin4x+cos4x
dx
Solution



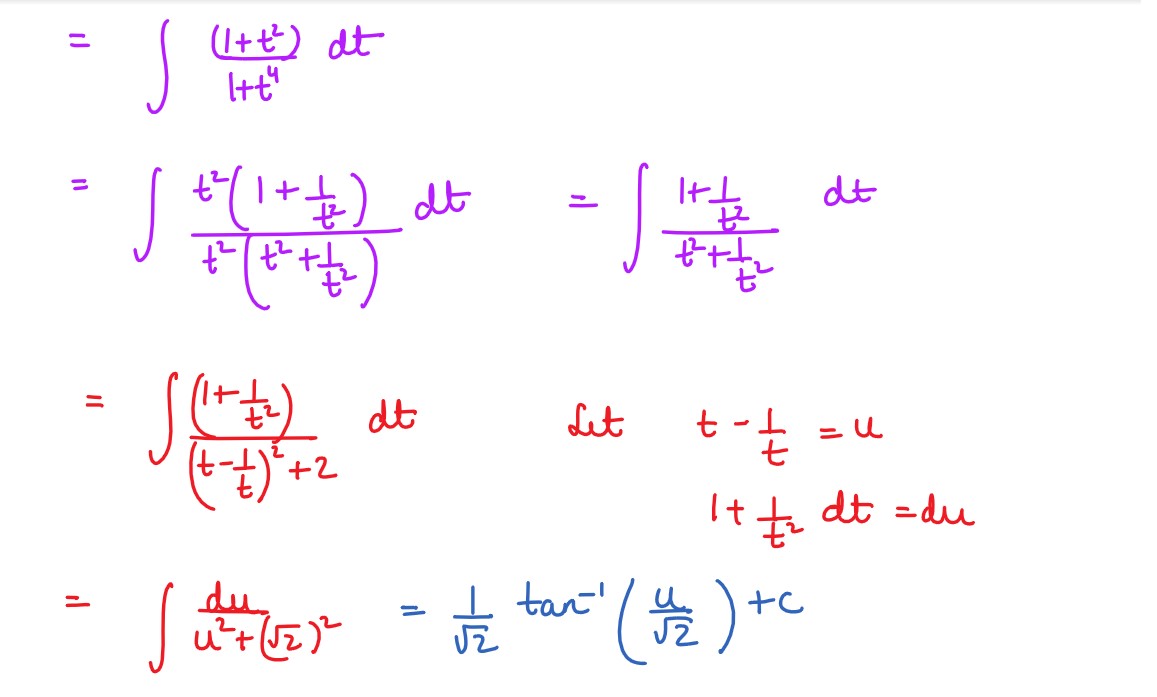

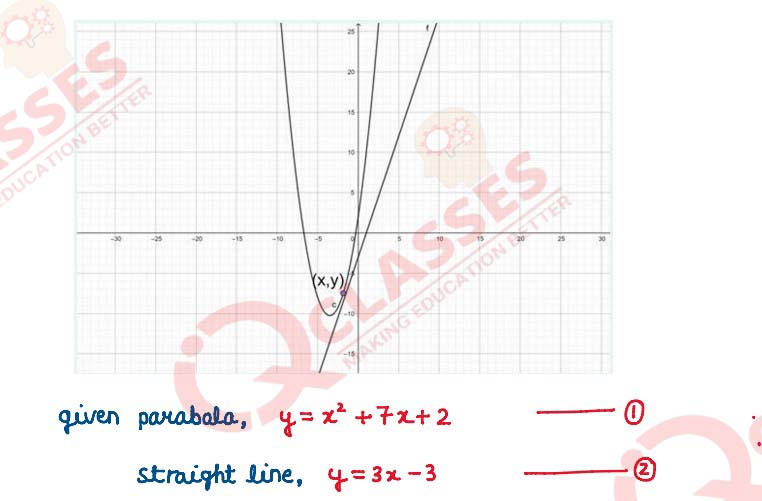
(i) Find the maximum volume of the cylinder which can be inscribed in a sphere of radius
3√3 𝑐𝑚. (find the answer in terms of 𝜋)
OR
(ii) Find the coordinates of a point on the curve 𝑦 = 𝑥
2 + 7𝑥 + 2 which is closest to the
straight line 𝑦 = 3𝑥 − 3.
Solution







A biased four-sided die with faces labelled 1, 2,3 and 4 is rolled and recorded. Let 𝑋 be the
result obtained when the die is rolled. The probability distribution for 𝑋 is given in the
following table where p and 𝑞 are constants.
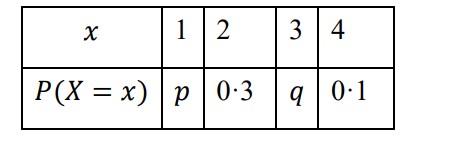
For the probability distribution, it is known that 𝐸(𝑋) = 2. Find 𝑝 and 𝑞.
Also, find 𝑃(𝑋 > 2).
Ajay plays a game with this four-sided die. In this game he is allowed a maximum of five
rolls. His score is calculated by adding the results of each roll. He wins the game if his score
is at least 10. After 3 rolls, Ajay has score of four points. Assuming that rolls of the die are
independent, find the probability that Ajay wins the game.
Solution



SECTION B
Question 15
In subparts (i) and (ii) choose the correct options and in subparts (iii) to (v), answer the
questions as instructed.
(i) If 𝑎⃗ = 𝑖̂+ 2𝑗̂+ 3𝑘̂ and 𝑏⃗⃗ = -𝑖̂+ 2𝑗̂+ 𝑘̂ and 𝑐⃗ = 3𝑖̂+ 𝑗̂, find 𝑡 such that 𝑎⃗ +
𝑡𝑏⃗⃗ is
perpendicular to 𝑐⃗ is
- 0
- 5
- 4
- 2
(ii) The planes 2x – y + 4z = 5 and 5x – 2·5y + 10z = 6 are
- parallel
- intersect on y axis
- perpendicular
- pass through (0, 0, 5/4)
(iii) Find a vector of magnitude of 10 units and parallel to the vector 2𝑖̂+ 3𝑗̂− 𝑘̂.
(iv) Find the position vector of a point R which divides the line joining the two-points 𝑃
and 𝑄 with position vectors 2𝑖̂+𝑗̂and 𝑖̂− 2𝑗̂ respectively in the ratio of 2:1 externally.
(v) Find the equation of the plane with intercept 3 on the 𝑦 − axis and parallel to 𝑥𝑧 −plane.
Solution






(i) Find the area of the triangle whose adjacent sides are 𝑖̂+ 4𝑗̂– 𝑘̂ and 𝑖̂+ 𝑗̂+ 2𝑘̂
OR
(ii) For any two non-zero vectors 𝑎⃗ and 𝑏⃗⃗, if | 𝑎⃗.𝑏⃗⃗ |=|𝑎⃗ ×𝑏⃗⃗|, then find the angle
between them.
Solution


Show that
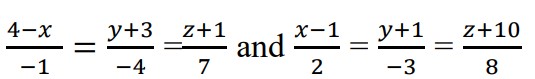
intersect each other. Also find out
the point of intersection.
OR
(ii) Find the equation of the plane passing through the points (0,4, −3) and (6, −4,3) if
the sum of their intercepts on three axes is 0.
Solution







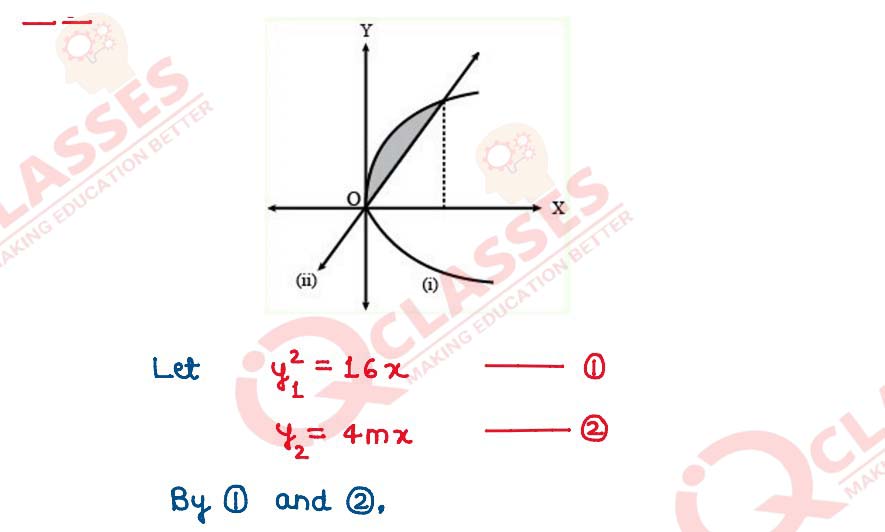
If the area is bounded by the parabola 𝑦2 = 16𝑥 and the line 𝑦 = 4𝑚𝑥 is 1/12 sq units, then using integration, find the value of 𝑚. (𝑚 > 0).
Solution



SECTION C
Question 19
In subparts (i) and (ii) choose the correct options and in subparts (iii) to (v), answer the
questions as instructed.
(i) Which relation is correct for breakeven point where 𝑅(𝑋) is revenue function and 𝐶(𝑥) is
cost function?
- 𝑅(𝑋) > 𝐶(𝑋)
- 𝑅(𝑋) < 𝐶(𝑋)
- 𝑅(𝑋) = 𝐶(𝑋)
- 𝑅(𝑋) = 2𝐶(𝑋)
(ii) If correlation coefficient 𝑟 = 0, then regression lines are
- parallel to each other.
- not mutually perpendicular.
- parallel to coordinate axis.
- overlapping lines.
(iii) Average revenue of a commodity is given by 𝐴𝑅(𝑥) = 𝑎 +𝑏/𝑥. Find the demand function when
marginal revenue is zero.
(iv) If 𝑅(𝑋) = 36𝑥 + 3𝑥2 + 5 then find actual revenue from selling 50th item.
(v) For a given bi-variant distribution, the mean of variable 𝑥 = 4 and the mean of
variable 𝑦 = 6. Find the point of intersection of two regression lines.
Solution

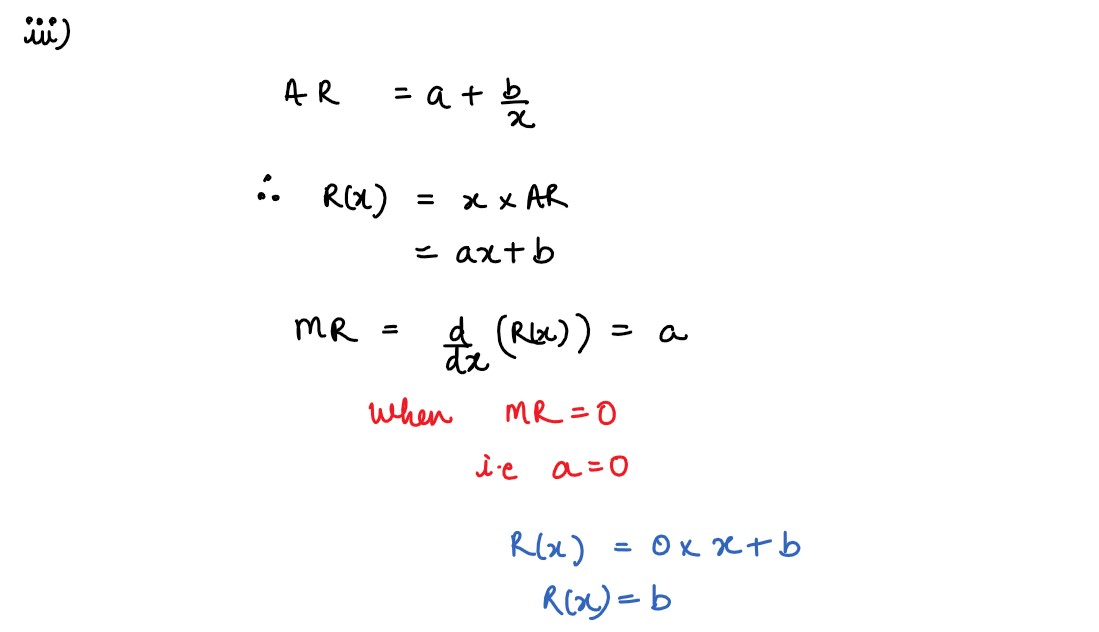

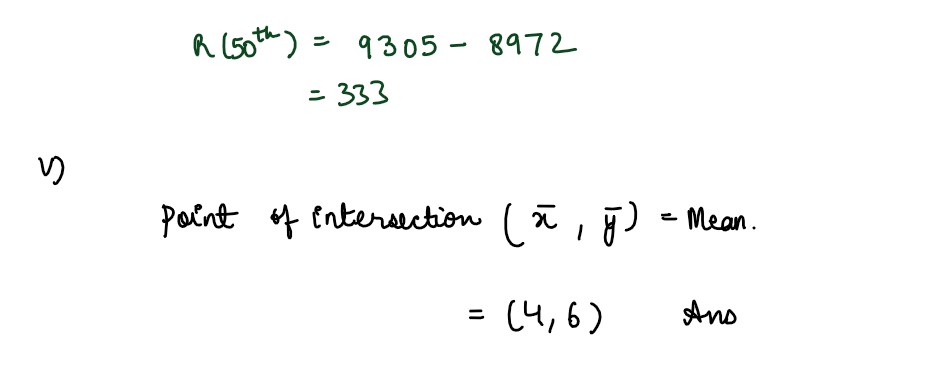
(i) The total revenue function R(x) = x + 2x3– 3·5x2
. Find the point where marginal
revenue curve cuts the co-ordinate axis.
OR
(ii) For the revenue function 𝑅(𝑥) =
bx
/
a+x
, show that the marginal revenue function is
increasing for all 𝑏 < 0 and 𝑎> 0.
Solution
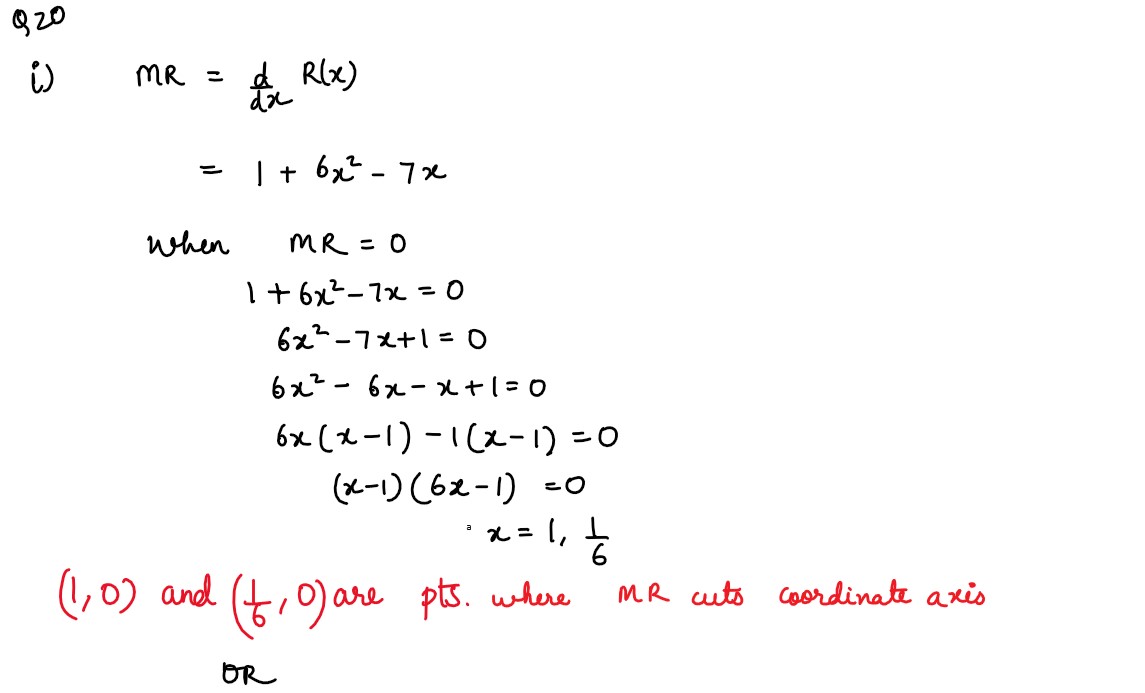
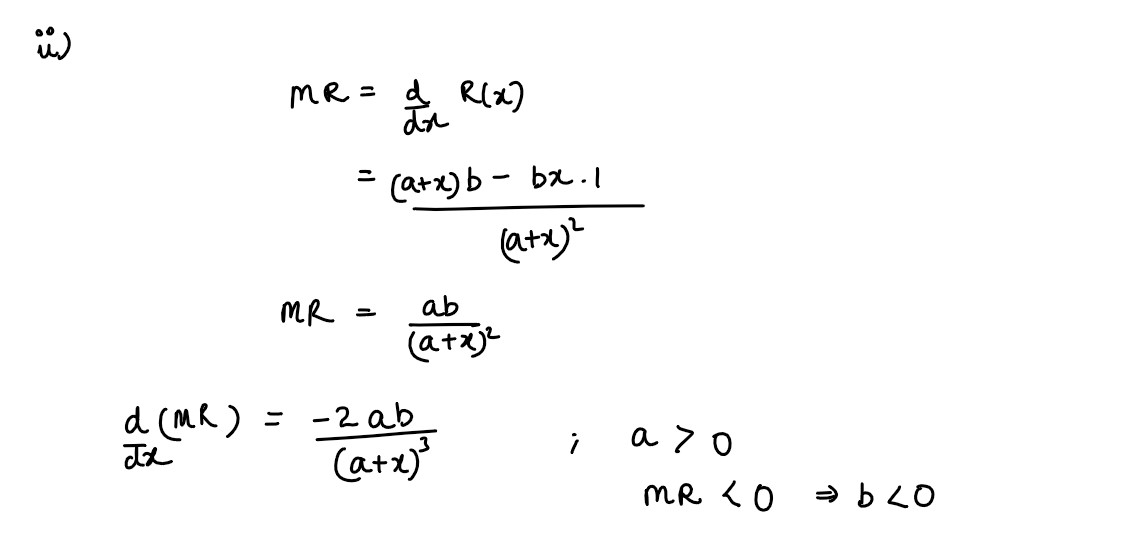
The line of regression of marks in Maths (𝑋) and marks in English (𝑌) for a class of 50 students is 3𝑌 − 5𝑋 + 180 = 0. The average score in English is 44 and variance of marks in Maths is 9/16 𝑡ℎ of the variance of marks in English. Find the average score in Maths. Also, find out the coefficient of correlation between marks in Maths and English.
Solution


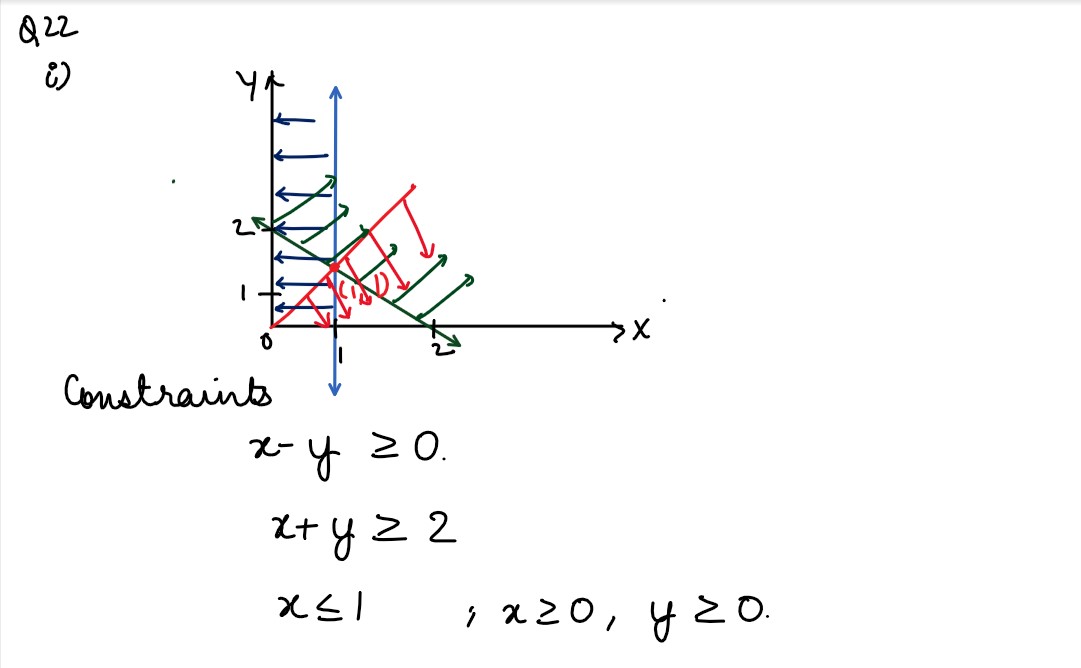
(i) Solve the following linear programming problem graphically and interpret your result
of 𝑍 = 2𝑥 – 5𝑦 subject to the constraints 𝑥 + 𝑦 ≥ 2, 𝑥 − 𝑦 ≥ 0, 𝑥 ≤ 1, 𝑥 ≥0, 𝑦 ≥ 0.
OR
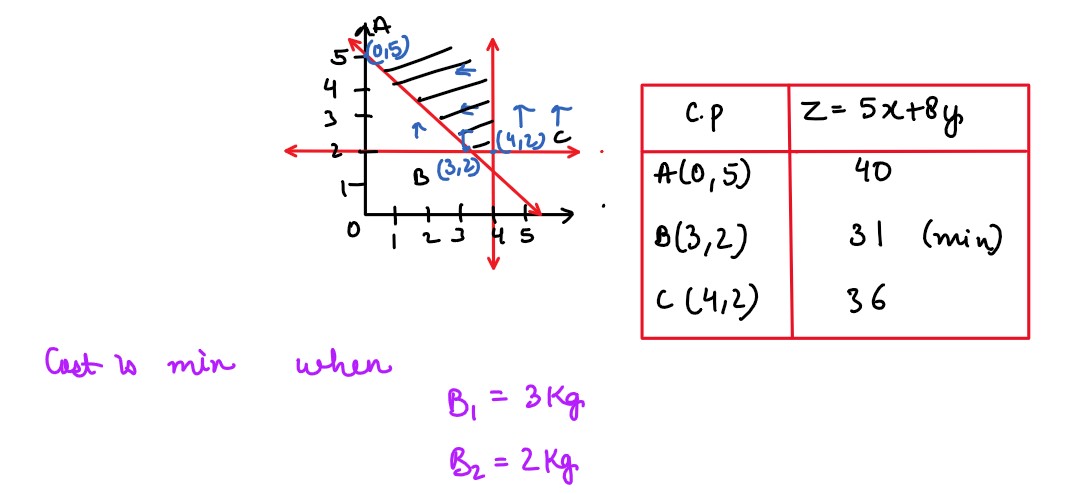
(ii) The standard weight of a special purpose brick is 5 kg and it must contain two basic
ingredients B1 and B2 . B1 costs ₹ 5 per kg and B2 costs
₹ 8 per kg. Strength
considerations dictate that the brick should not contain more than 4 kg of B1 and
minimum 2 kg of B2 .Since the demand for the product is likely to be related to the
price of the bricks, find the minimum cost of the brick satisfying the above conditions.
Formulate this situation as an L.P.P. and solve it graphically.
Solution
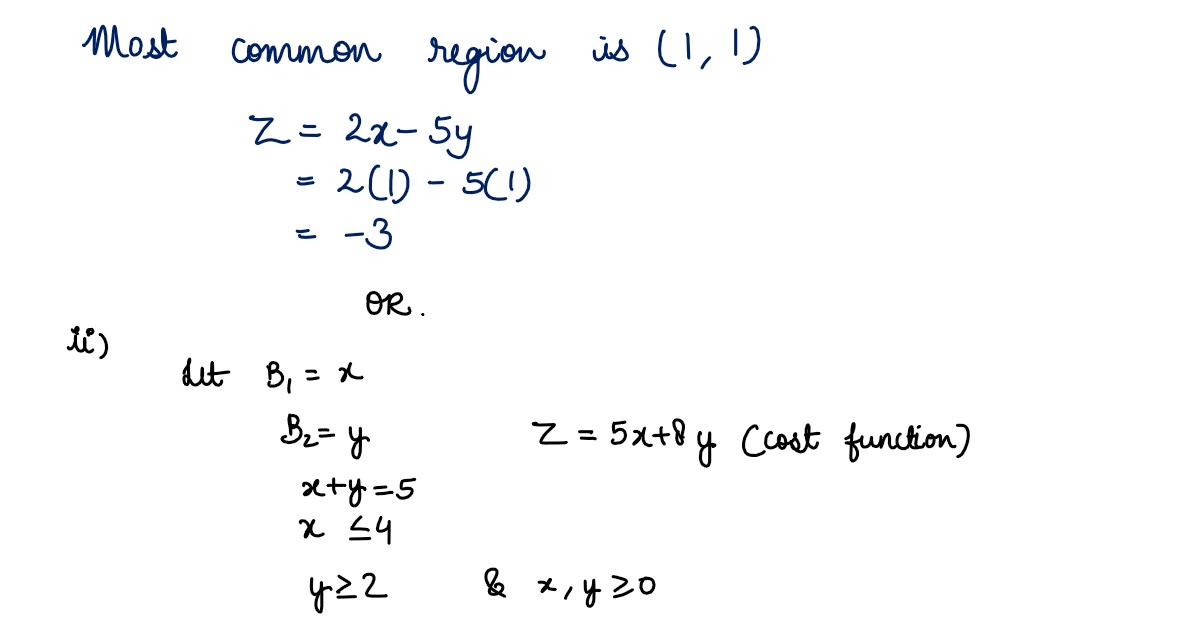

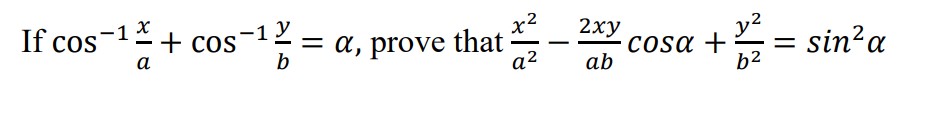
Add a comment