Class 12 ISC Maths Specimen Question Paper 2024

Maximum Marks: 70

Time Allowed: Three hours

(Candidates are allowed additional 15 minutes for only reading the paper.
They must NOT start writing during this time).

This paper is divided into four sections – A, B, C and D.

Answer all questions.

Section A consists of one question having sub-parts of one mark each.

Section B consists of seven questions of two marks each.

Section C consists of nine questions of three marks each, and

Section D consists of three questions of five marks each

. Internal choices have been provided in two questions each in Section B, Section C and Section D.

The intended marks for questions are given in brackets [ ].

All working, including rough work, should be done on the same sheet as and adjacent to the rest of the answer.

Answers to sub parts of the same question must be given in one place only.

A list of useful physical constants is given at the end of this paper.

A simple scientific calculator without a programmable memory may be used for calculations.

Section-A

Question 1

In subparts (i) to (x) choose the correct options and in subparts (xi) to (xv), answer the questions as instructed.

(i) P and Q are two matrices such that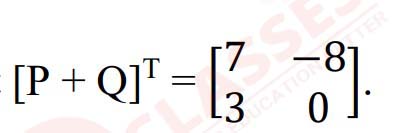

If P=,which one of the following is Q?

Solution

(ii) If ∫ sin^-1(𝑐𝑜𝑠𝑥)𝑑𝑥 = 𝑔(𝑥)-x²/2 + 𝑐, then 𝑔(𝑥) will be:

(a) π/2 x
(b) -π/2 x
(c) 0
(d) x/2

Solution

(iii) What is the value of cot (π/2 +tan^-1 1/√2)

(a) 1/√2
(b) π/2
(c) -1
(d) -1/√2

Solution

(iv) For what value of n is the given a homogenous differential equation?

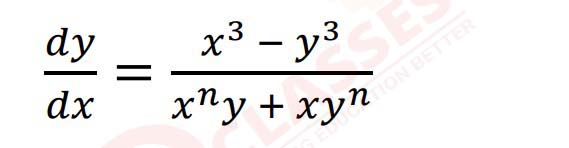
(a) 1
(b) 3
(c) 0
(d) 2

Solution

(v) Bhuvan is preparing chapati and curry for a dinner party at his home.

Let event A = Bhuvan prepares chapati well.
Let event B = Bhuvan cooks curry well.
Given P(A) = 0·40, P(B) = 0·30 and P(A and B) = 0·20

Which one of the following is true about the events A and B?

(a) They are mutually exclusive but not independent.
(b) They are independent but not mutually exclusive.
(c) They are both mutually exclusive and independent.
(d) They are neither mutually exclusive nor independent.

Solution

(vi)

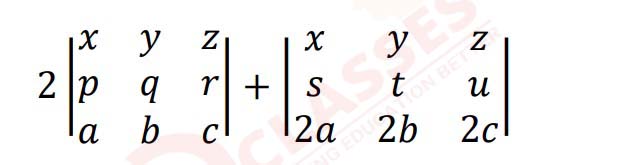
Which one of the following is equal to the above sum

Solution

(vii) Given below are the graphs of f(x) along with the statements. Which one of the following statements is NOT correct about the graphs?

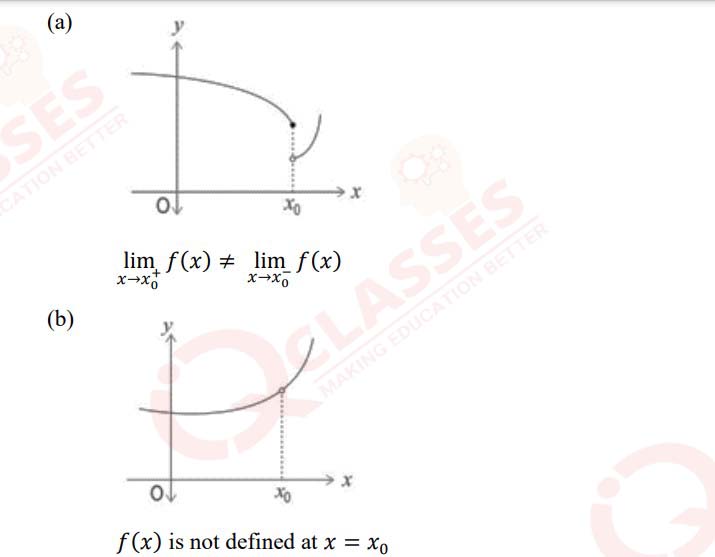
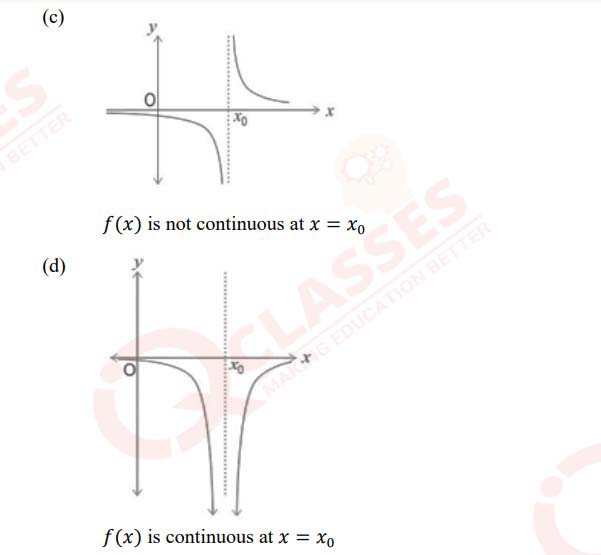
Solution

(viii) Shown below is the graph of a function, g(x).

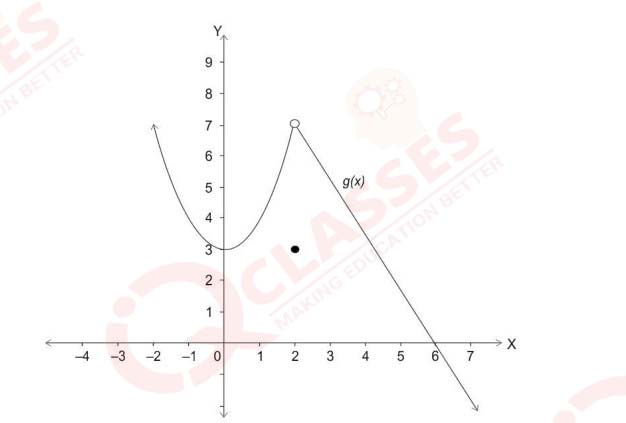
Which of the following is true?

(a) g(x) is continuous and differentiable at x = 2
(b) g(x) is continuous but not differentiable at x = 2
(c) g(x) is not continuous but differentiable at x = 2
(d) g(x) is neither continuous nor differentiable at x = 2

Solution

(ix) Statement 1: The function 𝑓: 𝑁 ⟶ 𝑁 given by f(x) = 5x is one to one and onto.

Statement 2: The function 𝑓: 𝑅 ⟶ 𝑅 given by f(x) = 5x is one to one and onto.

Which one of the following options is correct?
(a) Both the statements are true.
(b) Both the statements are false.
(c) Statement 1 is true and Statement 2 is false.
(d) Statement 1 is false and Statement 2 is true.

Solution

(x) Matrix P is a skew-symmetric matrix of odd order.

Assertion: The inverse of matrix P does not exist.
Reason: The determinant of matrix P is zero.

(a) Both Assertion and Reason are true and Reason is the correct explanation for Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation for Assertion.
(c) Assertion is true and Reason is false.
(d) Assertion is false and Reason is true

Solution

(xi) The function f:X ->Y is not invertible.State the reason

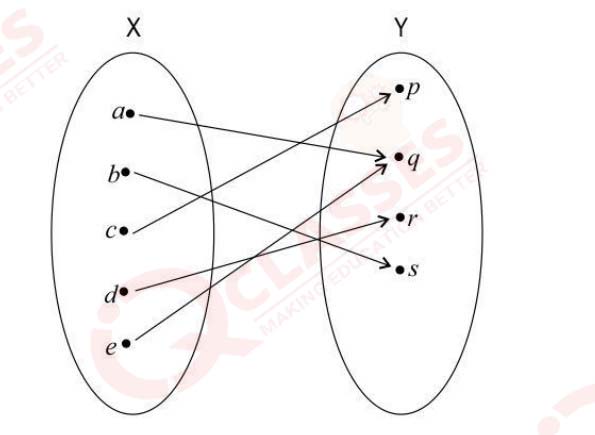
Solution

(xii) If A=
(5 x
y 0 ) and A is symmetric, then write the relation between x and y

Solution

(xiii) If a relation 𝑅 on the set 𝐴 = {1, 2, 3} be defined by 𝑅 = {(1, 2), (2, 1)} then classify the function 𝑅.

Solution

(xiv) A company has estimated that the probabilities of success for three products introduced in the market are 1/3, 2/5 and 2/3 respectively. Assuming independence, find the probability that at least one product is successful

Solution

(xv) Dobleron, a chocolate is known for its distinctive shape and its taste. The quality assurance team of the brand undertakes quality test in two steps:

• Step 1: 30 out of every 990 chocolate bars are randomly picked for physical examination, where the shape of the bar is examined.

• Step 2: For every 30 chocolate bars whose shape is examined, 1 chocolate bar is randomly picked for chemical examination, where the composition and taste of the chocolate is examined.

If one chocolate bar is randomly picked out of 990 bars, what is the probability that it was not chemically examined, provided it was physically examined?

Solution

Question 2

(i) The table below shows some of the values of differentiable functions u and v and their derivatives.

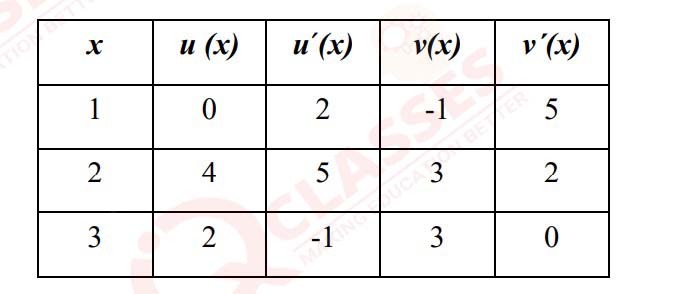
If r(x) = u(v(x)), find r'(2).

OR (ii) If 𝑓(𝑥) = 𝑥3 − 48𝑥, find the interval where f:R → R is decreasing

Solution

Question 3

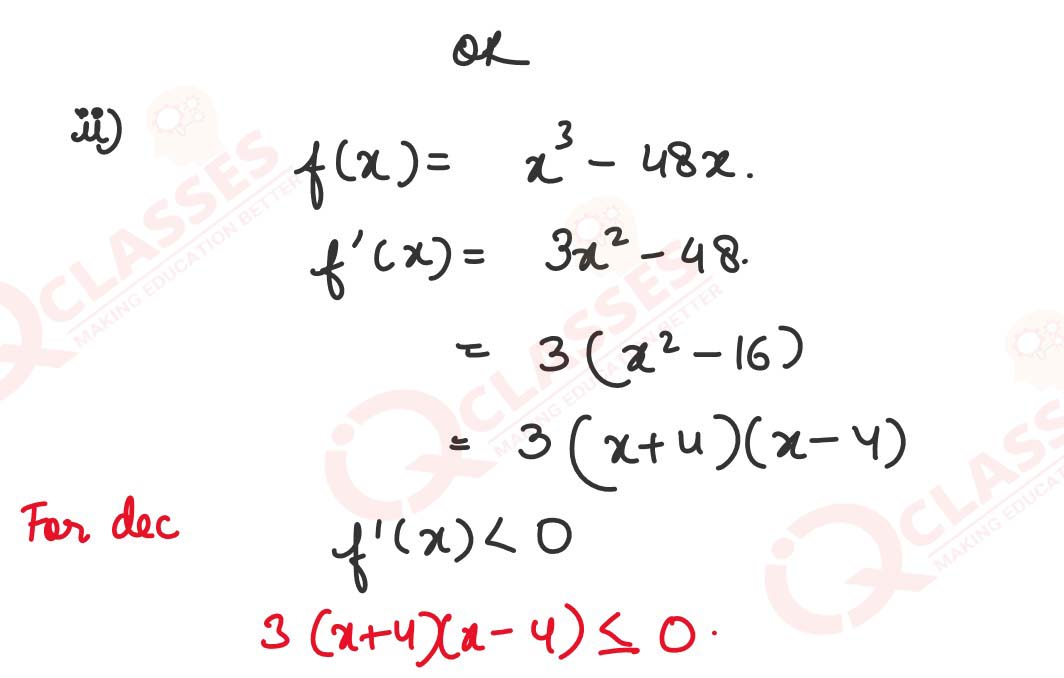
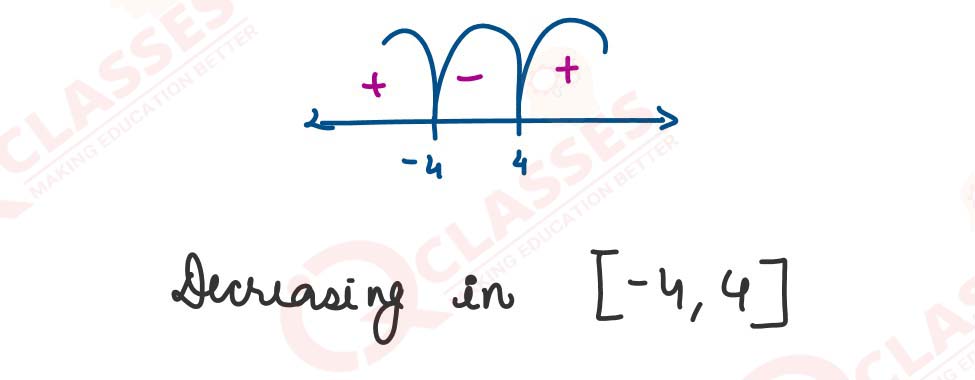
Evaluate: ∫^π/2_-π/2 |𝑠𝑖𝑛𝑥|𝑑x

Solution

Question 4

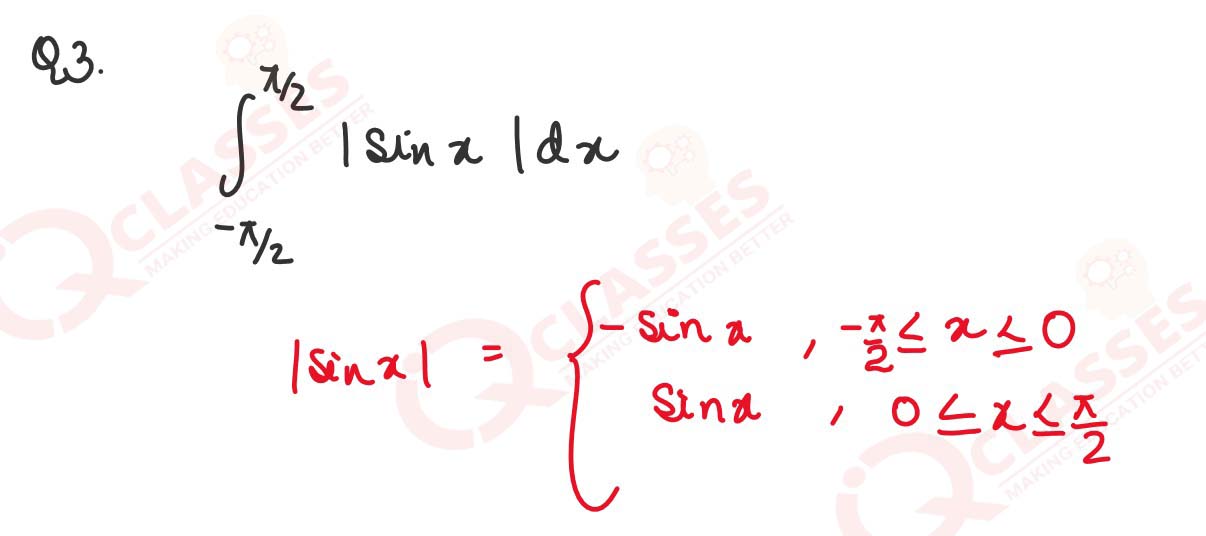
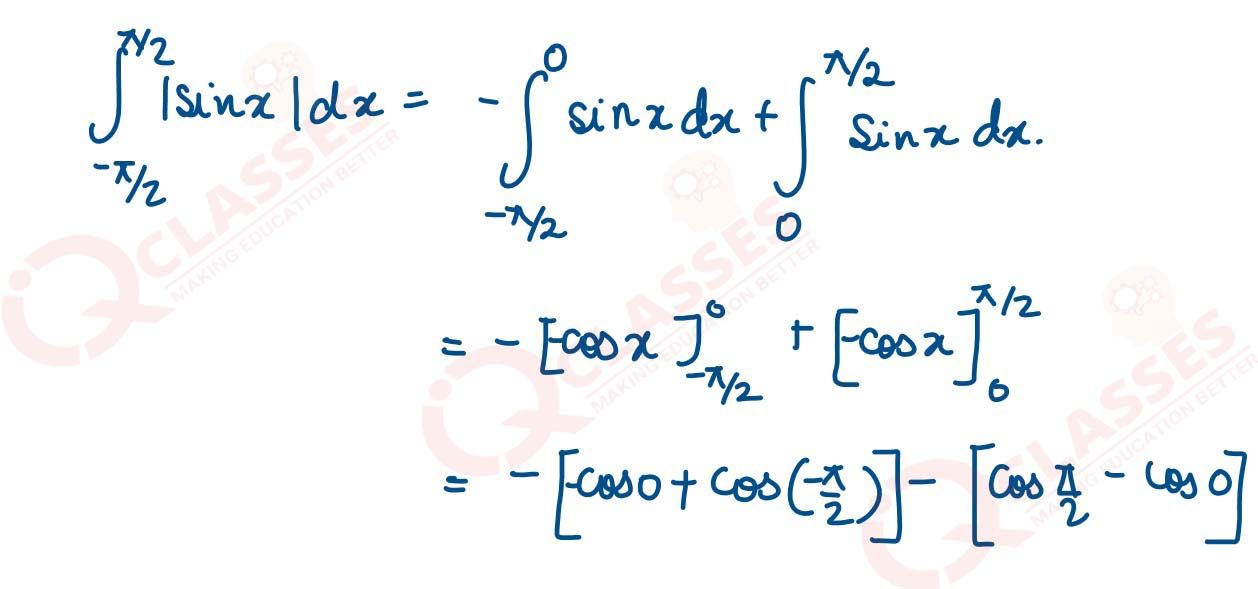
Find the point on the curve 𝑦 = 𝑥² + 2𝑥 − 1, where the tangent is parallel to x- axis.

Solution

Question 5

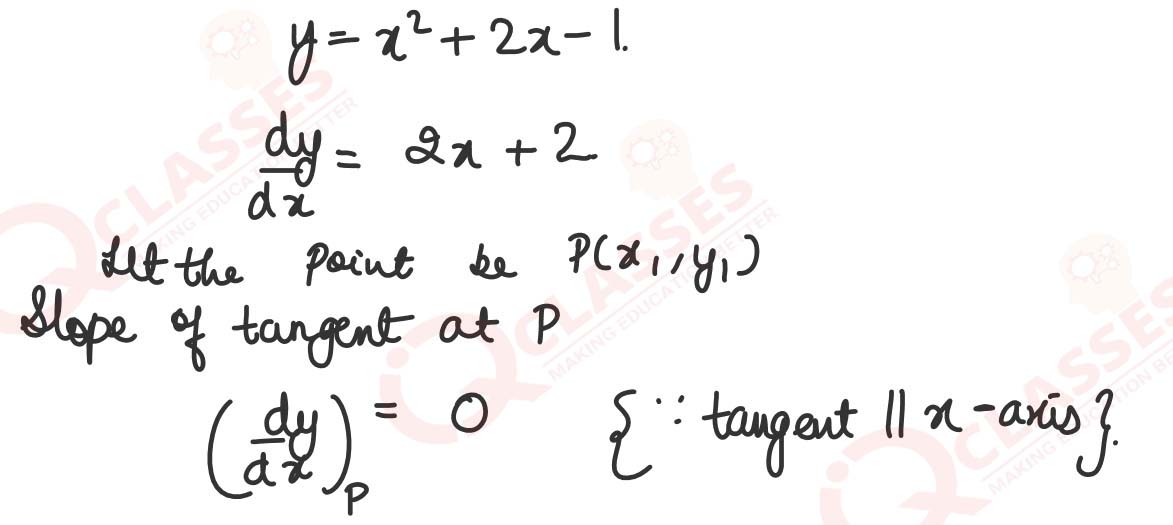
(i) Evaluate: ∫ (5-3x²/6-x³+5x) dx

OR

(ii) Evaluate: ∫xe^x dx

Solution

Question 6

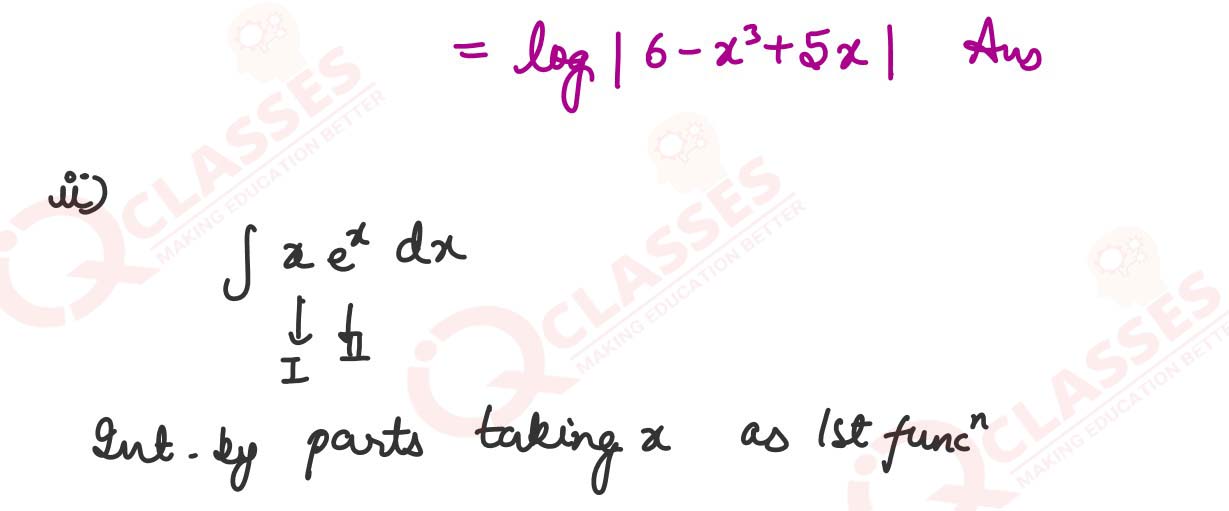
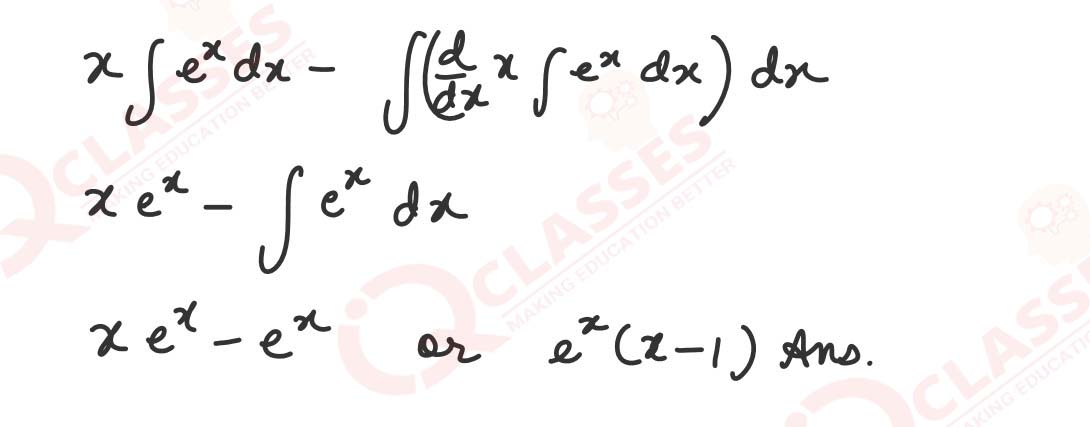
Find the domain of the function cos^-1 𝑥 + 𝑠𝑖𝑛x

Solution

Question 7

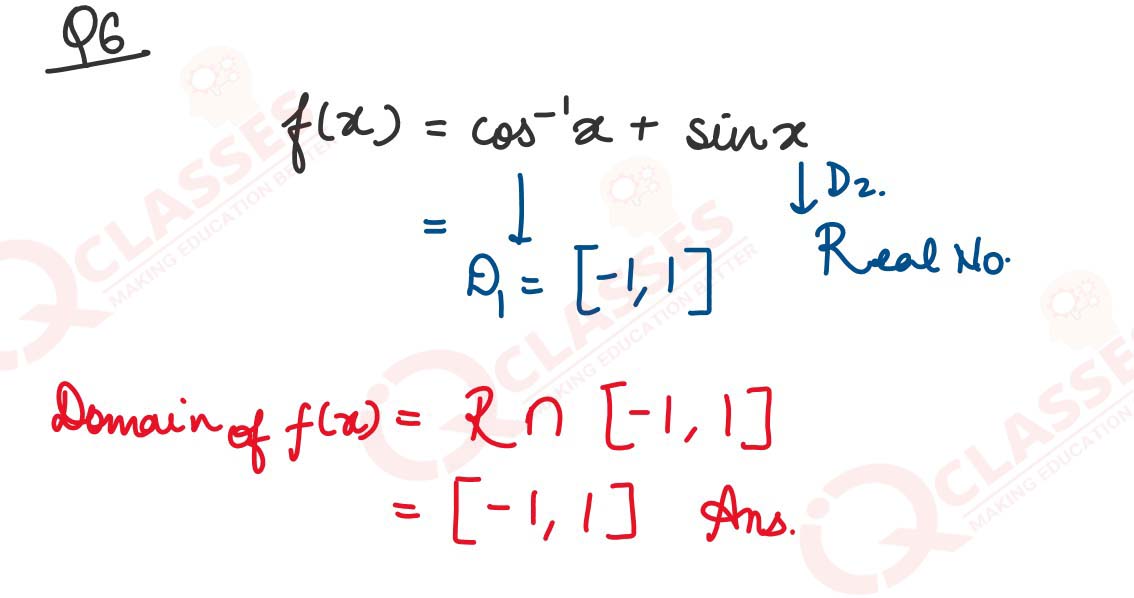
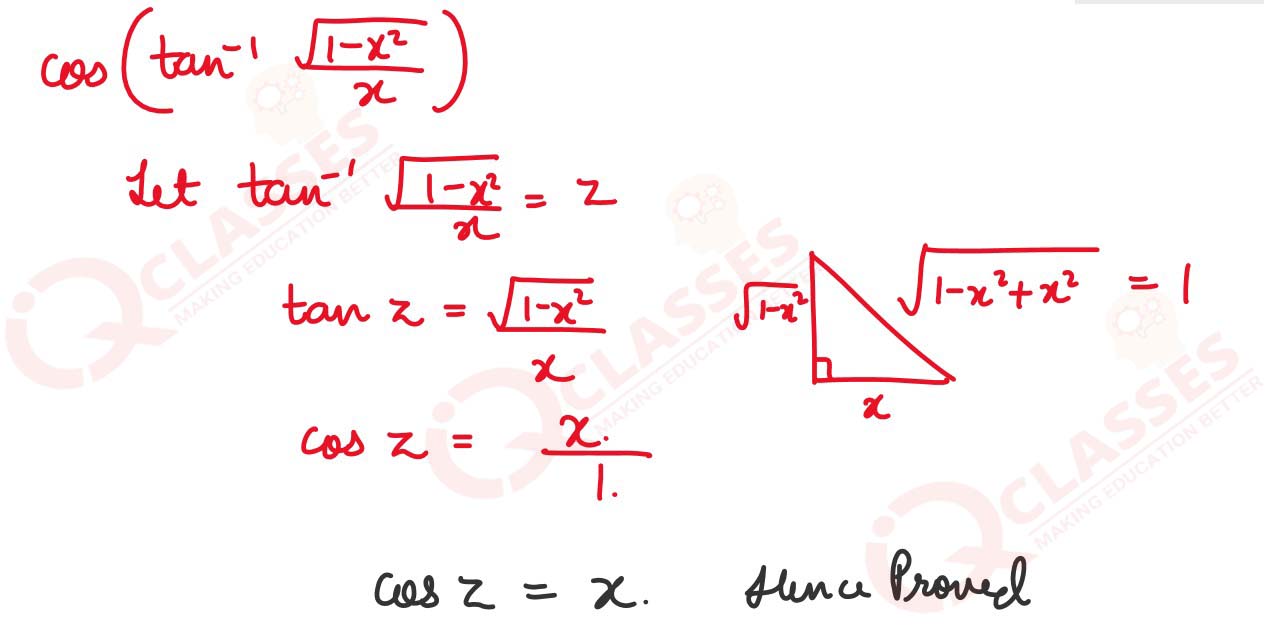
Prove that cos [tan-1 {cot (sin^-1x)}] = x.

Solution

Question 8

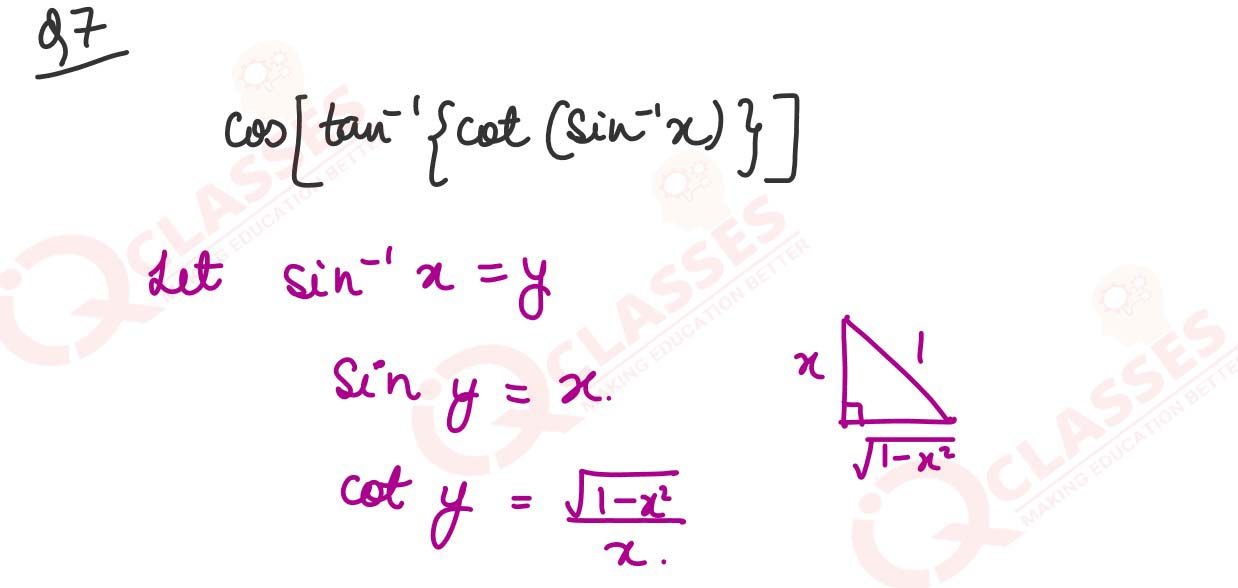
Evaluate: ∫ 9x³ +63 x²/x⁴+14 x³-9x² dx

Solution

Question 9

(i) Shown below is a function which is differentiable at x = 3

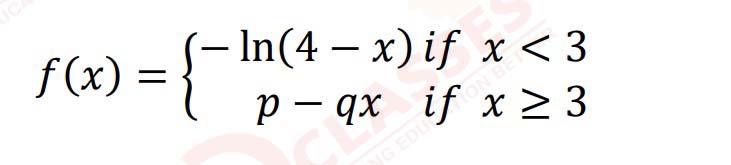
Find the values of p and q, where they are real numbers. Show your steps and give a valid reason.

OR

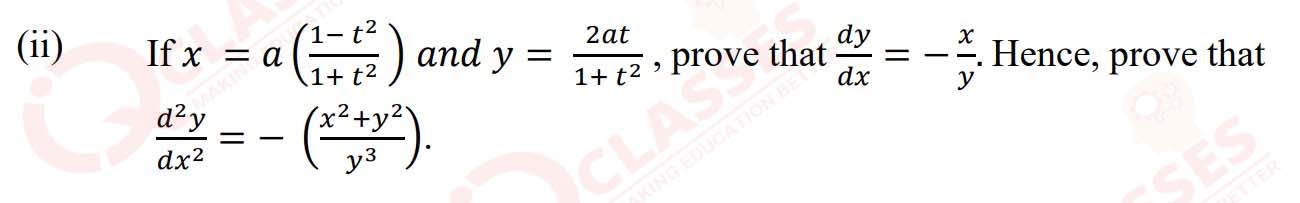
Solution

Question 10

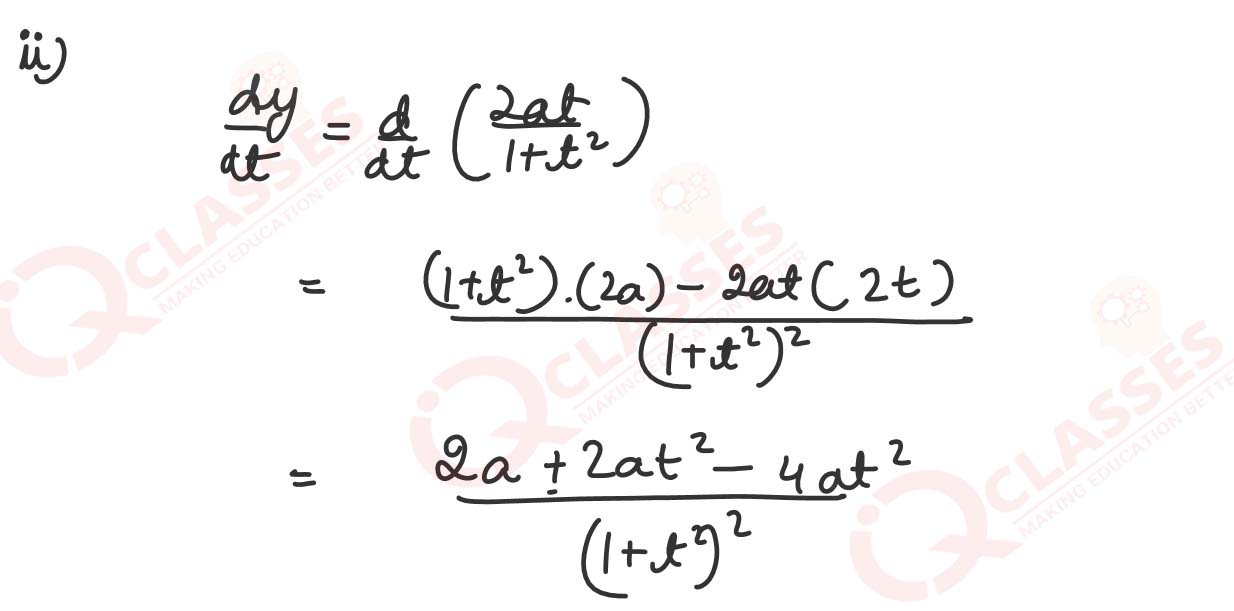
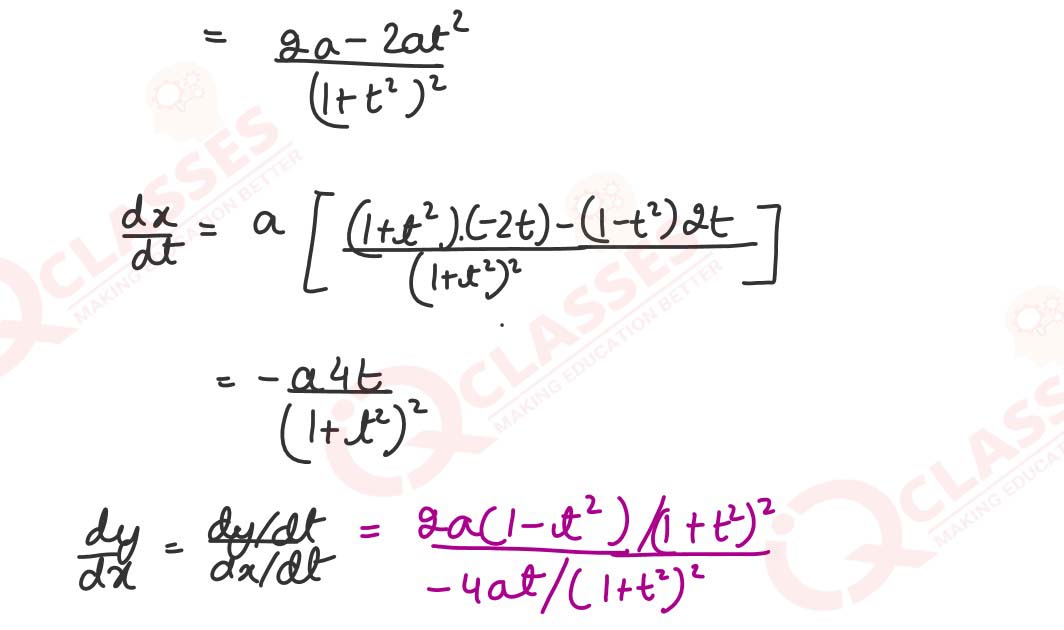
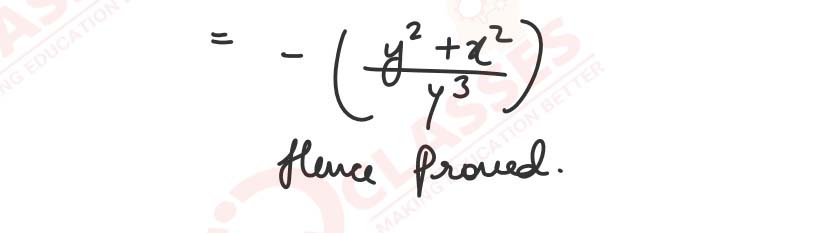
(i) There are two boxes, Box 1 and Box 2. Each box has 8 red balls, 5 green balls, and 7 blue balls. Sahil takes one ball from Box 1 and places it in Box 2. He then draws two balls from Box 2 simultaneously.

(a) What is the probability of Sahil selecting a green ball from Box 1?

(b) After Sahil transfers a ball from Box 1 to Box 2, what is the probability of drawing one red ball and one green ball simultaneously from Box 2?

(c) Given that the balls drawn from Box 2 are red and green, what is the probability that the ball transferred from Box 1 to Box 2 was green?

(d) Prove that the probability mentioned in (c) is less than 15%

OR

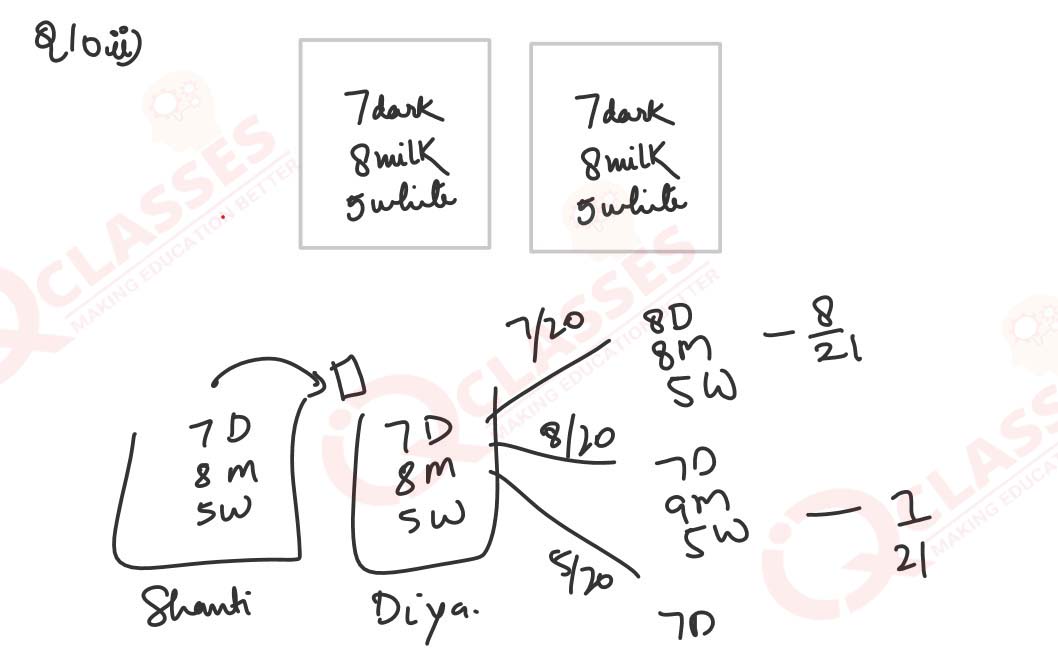
(ii) On a festival, two friends namely Shanti and Diya got identical gift bags containing 7 dark chocolates, 8 milk chocolates and 5 white chocolates each.

(a) What is the probability of Diya drawing a dark chocolate from Shanti’s bag?
(b) While Shanti was away, Diya transferred one chocolate from Shanti’s bag to hers without looking. What is the probability of drawing a dark chocolate from Diya’s bag after the transfer?
(c) Which one of the following probabilities is higher? Why? The probability of drawing a dark chocolate from Diya’s bag after the transfer or The probability of drawing a dark chocolate from Shanti’s bag before the transfer.

Solution

Question 11

Garima owns a cafe that serves burgers, samosas, and juice bottles. On a particular day, 100 items in total were sold. The number of burgers sold was thrice the number of samosas sold. Also, the number of samosas sold was 10 more than the number of juice bottles sold.

(i) Form a set of simultaneous equations for the above information.
(ii) Solve the set of equations formed in (i) by matrix method.
(iii) Hence, find the number of items sold in each category.

Solution

Question 12

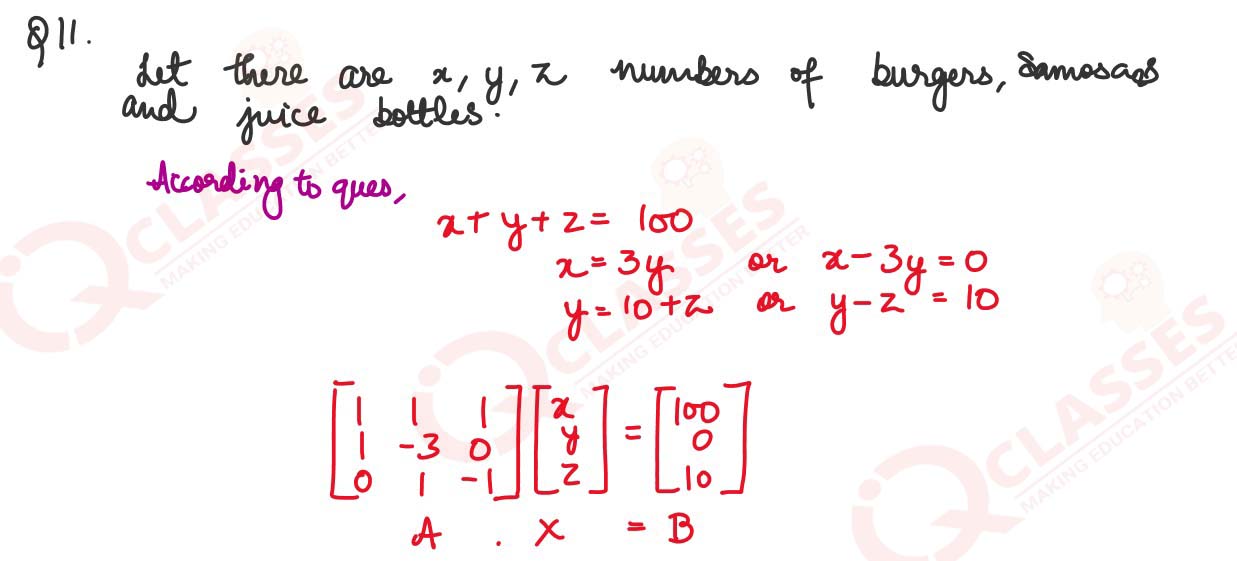
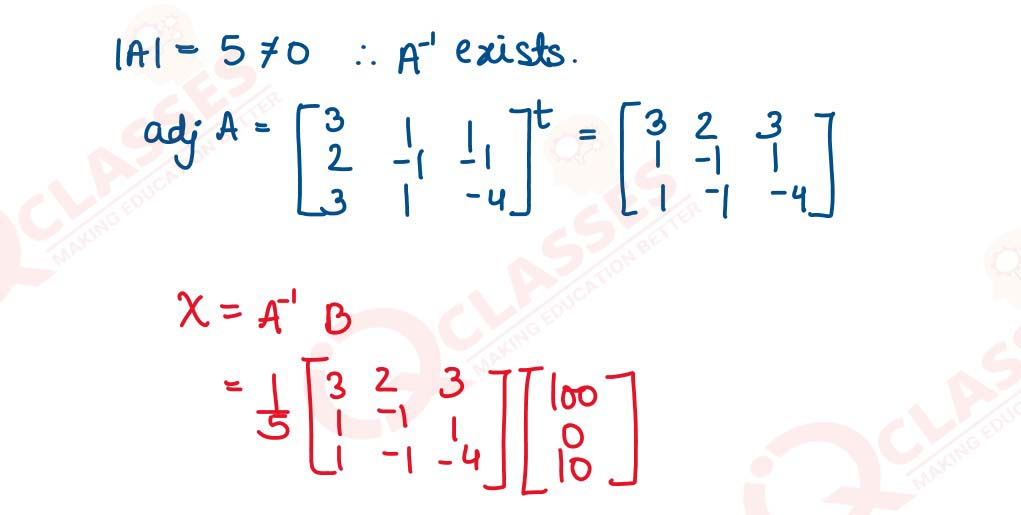
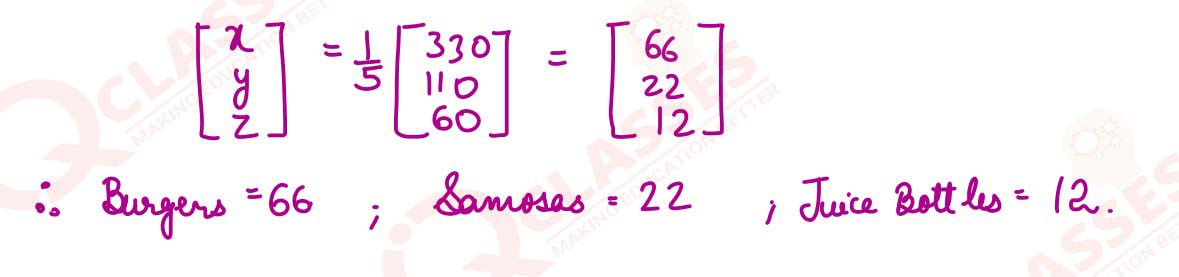
(i) Solve: 𝑥³𝑑𝑦 + (𝑥𝑦 − 1)𝑑𝑥 = 0.

Given 𝑦 = 3 − 𝑒 𝑤ℎ𝑒𝑛 𝑥 = 1/2 find 𝑦 𝑤ℎ𝑒𝑛 𝑥 = 1

OR

(ii) Evaluate: ∫ x²/x⁴+1 dx

Solution

Question 13

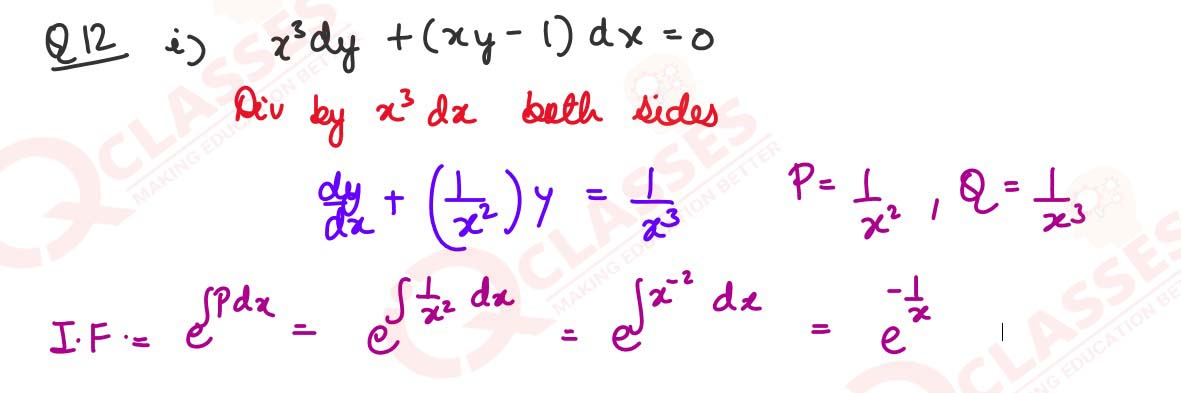
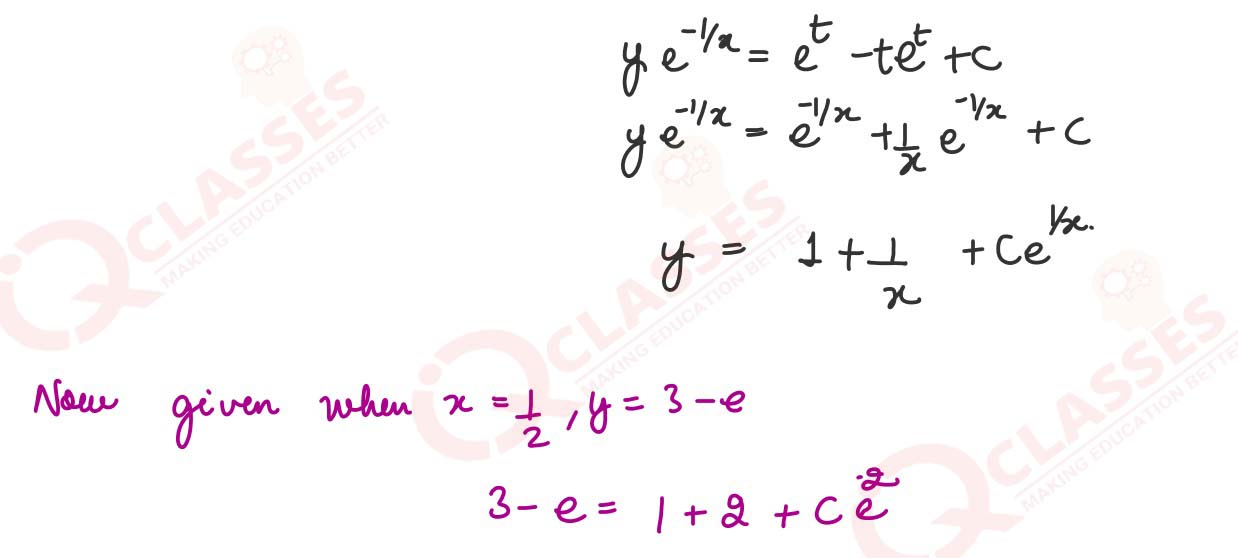
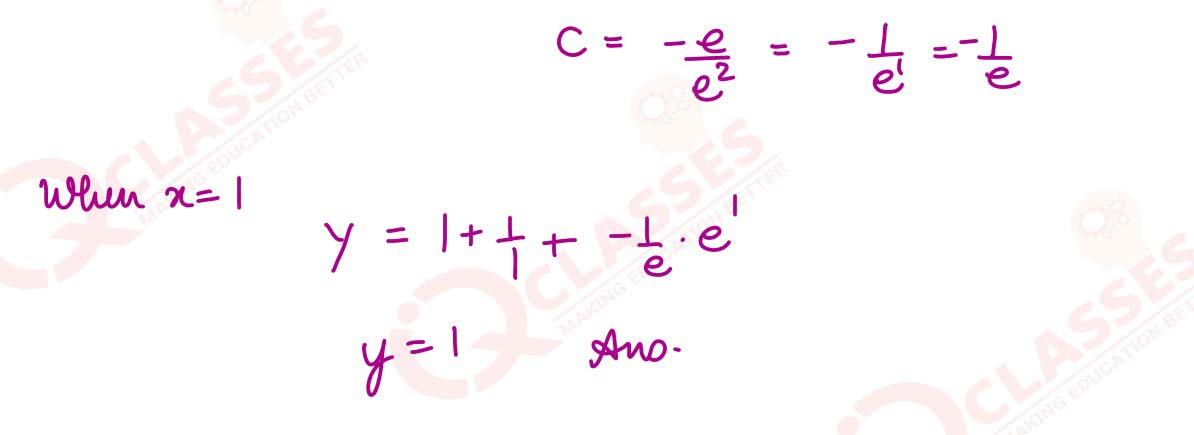
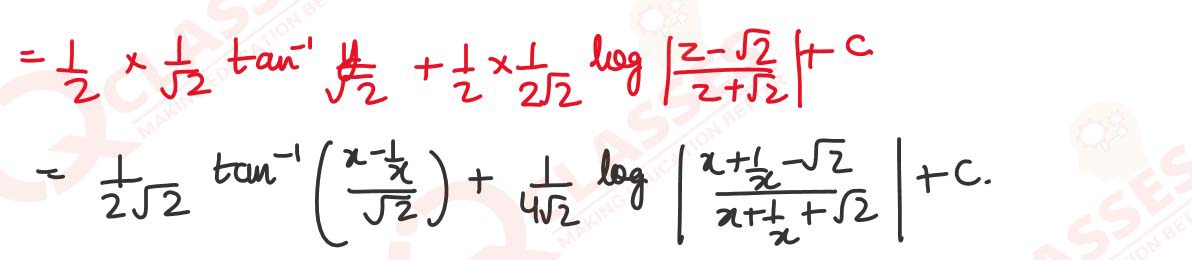
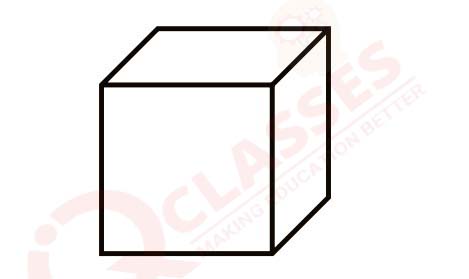
(i) A village chief wants to build a cuboidal water tank with a square base and an open top to store 50,000 Liters of water. The cost of the stainless-steel sheet required for construction is ₹ 60,000 per square meter.

Find the dimensions of the tank that will minimise the cost of the stainless steel sheet and determine the minimum cost.

OR

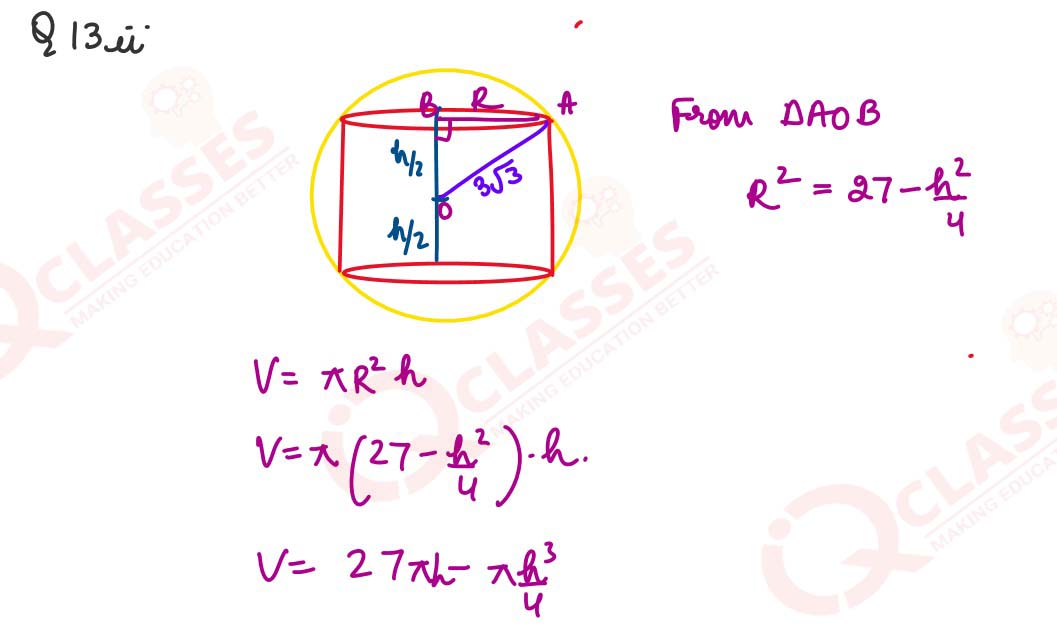
(ii) A paper weight manufacturer is designing a paper weight in the form of a cylinder inscribed in a sphere. He wants to keep the volume of the cylinder to be maximum. The radius of the sphere is 3√3 𝑐𝑚. Find the maximum volume of the cylinder

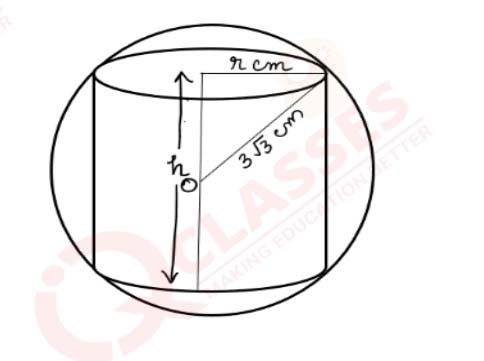
Solution

Question 14

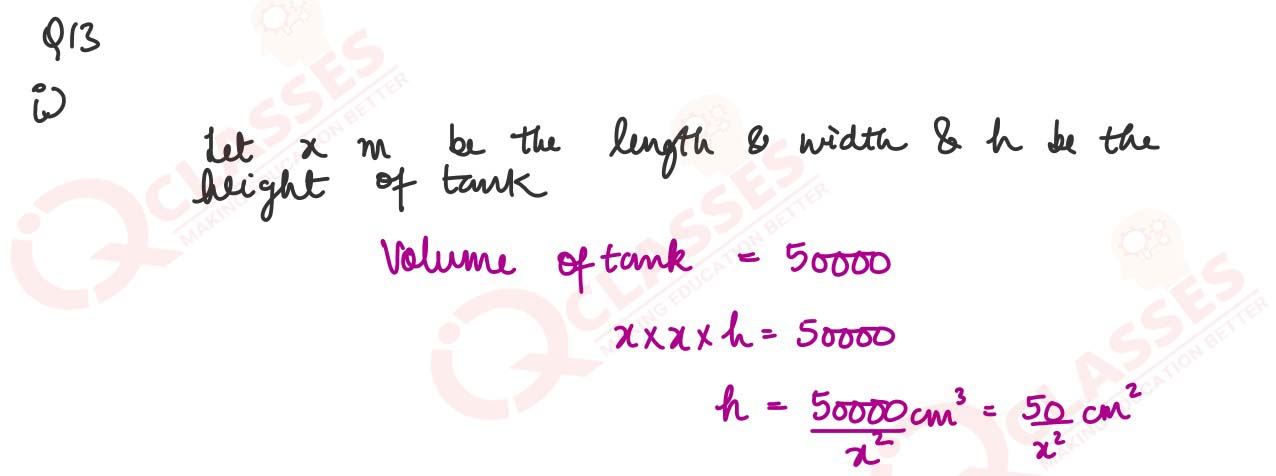
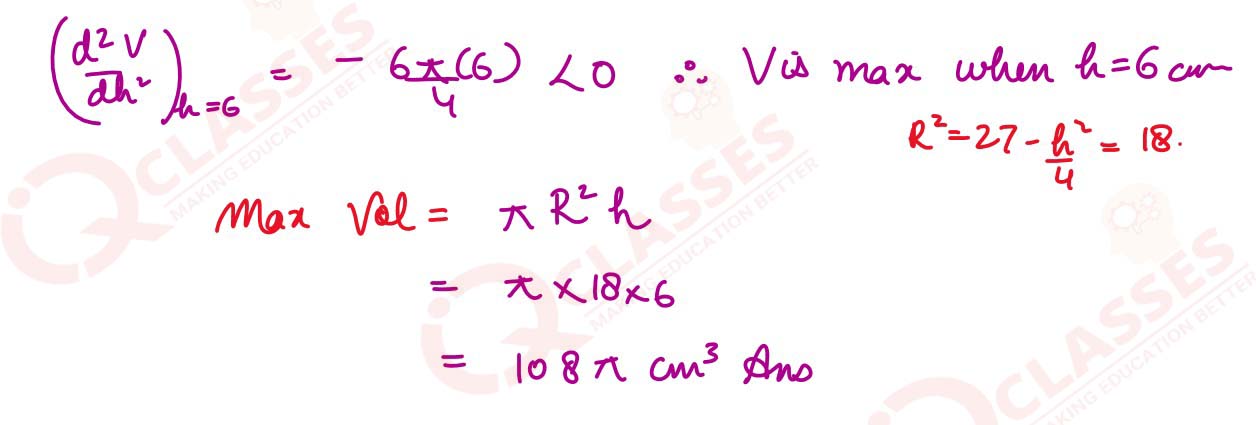
A group of class XI students designed a game for class XII students to be played at the farewell programme. They kept two sets of cards on the stage. Each set contained four cards numbered 1,2,3 and 4. Each student of class XII had to draw one card from each set simultaneously. The score a student received was defined as the difference between the numbers shown on the cards. The possible outcome of the score is given in the table below:

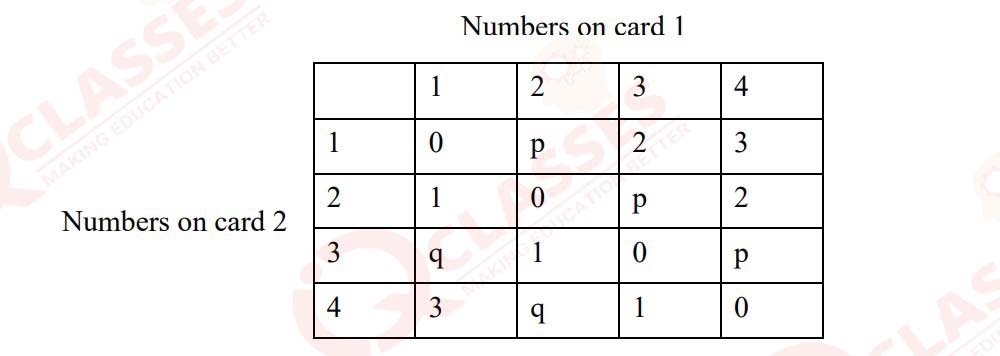
(i) Calculate the values of p and q in the above table.

(ii) Reshma plays the game once. Let the random variable ‘S’ represents Reshma’s score. Construct the probability distribution for ‘S’

(iii) Find the probability that Reshma’s score is at most 2.
(iv) Find Reshma’s expected score.

Solution

SECTION B

Question 15

In subparts (i) and (ii) choose the correct options and in subparts (iii) to (v), answer the questions as instructed.

(i) Observe the vector diagram shown below and the expression that follows.

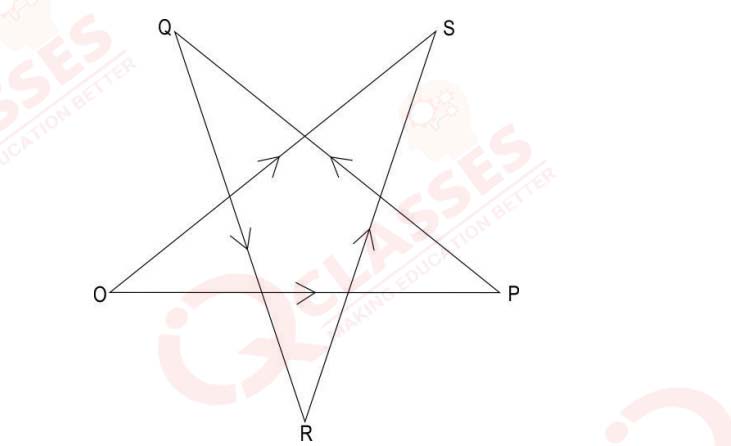
(1)SO
(2)OS
(3) −SO
(4) −OS
(a) only (1)
(b) only (2)
(c) only (1) and (4)
(d) only (2) and (3)

(ii) Prove that (1,1,1) cannot be the direction cosine of the straight line.

(iii) If u->=^i,v->=j and w-> k are unit vectors, what is the angle between (w-> x v-> ) and u-> ?

(iv) Find the intercepts on the coordinate axis cut off by the plane.

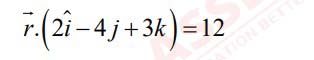
(a) 𝑎 = 6, 𝑏 = −3, 𝑐 = 4
(b) 𝑎 = 6, 𝑏 = 3, 𝑐 = 4
(c) 𝑎 = −6, 𝑏 = −3, 𝑐 = 4
(d) 𝑎 = 6, 𝑏 = −3, 𝑐 = −4

(v) Shown below is a cube.

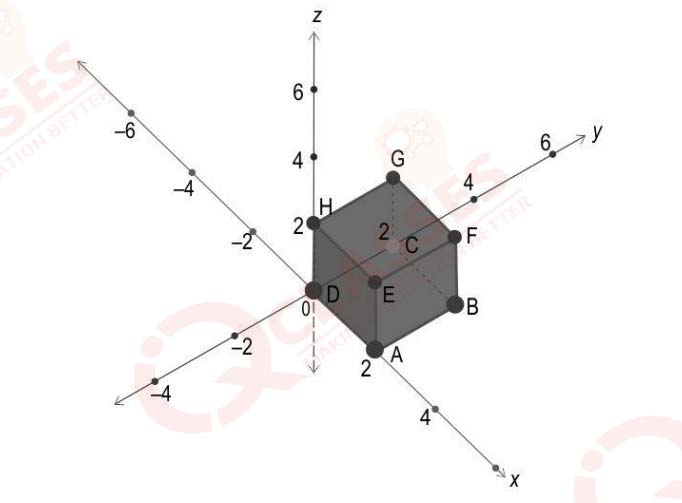
Find the equation of its diagonal which passes through the centre of the cube and also the origin.

Solution

Question 16

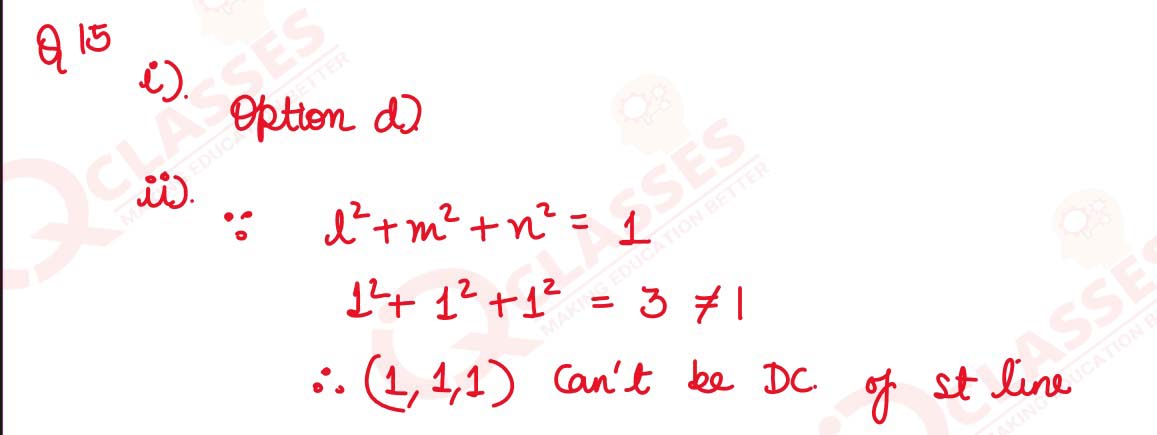
(i) (i) Given below are two vectors in their component form such that

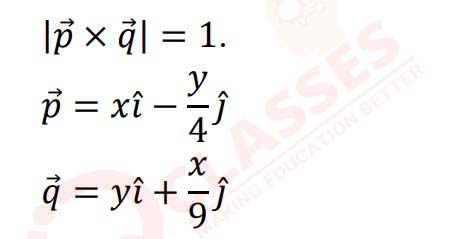
Find the relation between the variables 𝑥 𝑎𝑛𝑑 y

(ii) The position vectors of the points A and B are (2, −3, 2)and (2, 3, 1) respectively, then find the area of triangle 𝑂𝐴𝐵.

Solution

Question 17

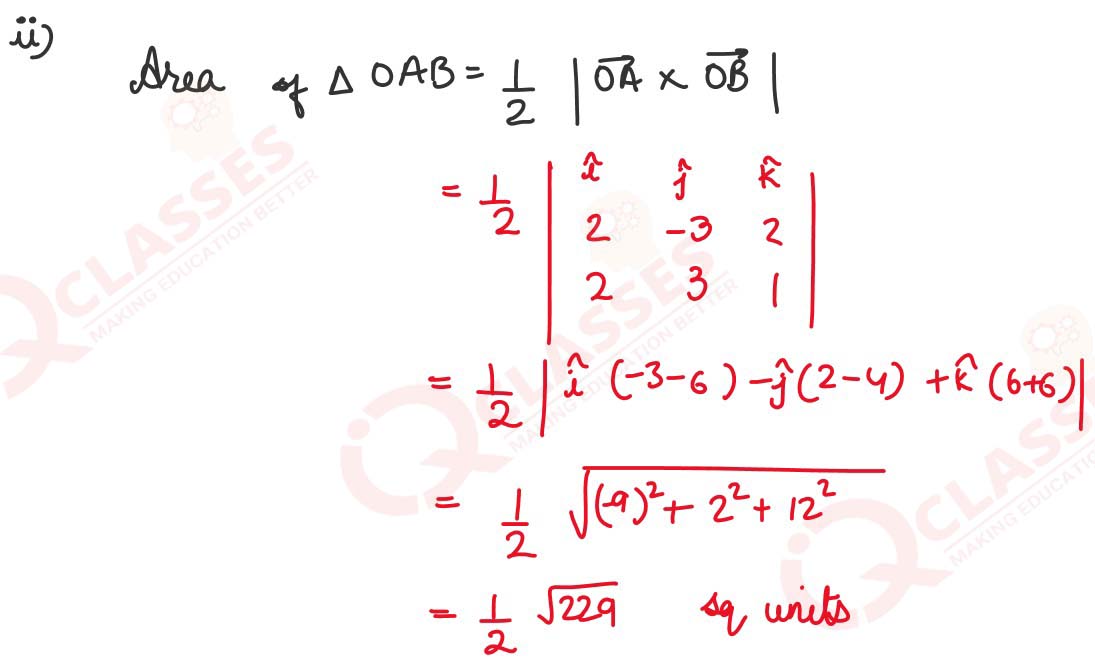
(i) (i) Shown below are equations of two planes

Is the point P (2, -3, 4) closer to plane 1 or plane 2? Find the angle between the planes.

OR

(ii) A line with positive direction cosines passes through the point P(-2, 3, 2) and makes equal angles with the coordinate axes. The line passes through the plane 3x - 4y + 2z = 11 at point Q.
Find the length of the line segment PQ.

Solution

Question 18

If the area enclosed between the curves 𝑦 = 𝑎𝑥² 𝑎𝑛𝑑 𝑥 = 𝑎𝑦², 𝑎 > 0, is 27 sq. unit, find the value of 'a'

Solution

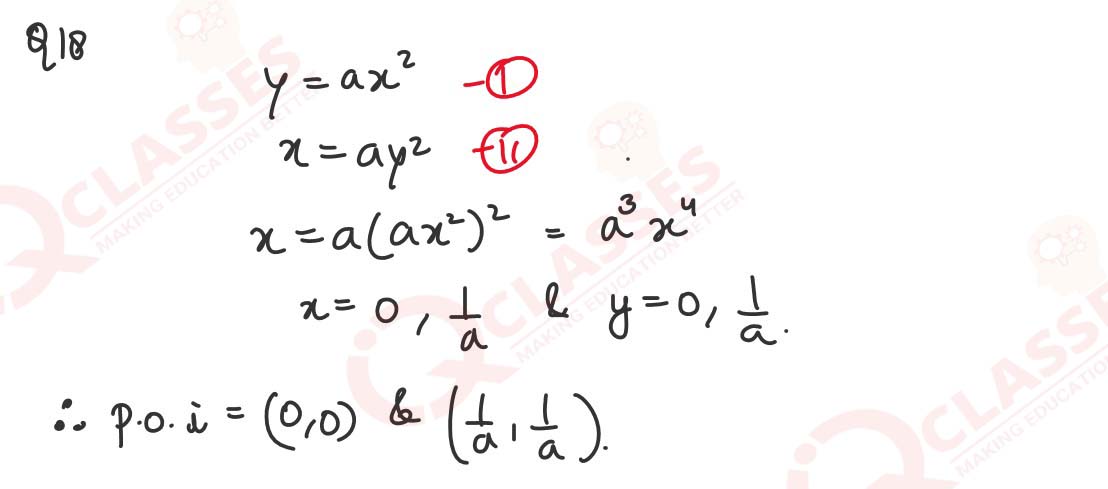
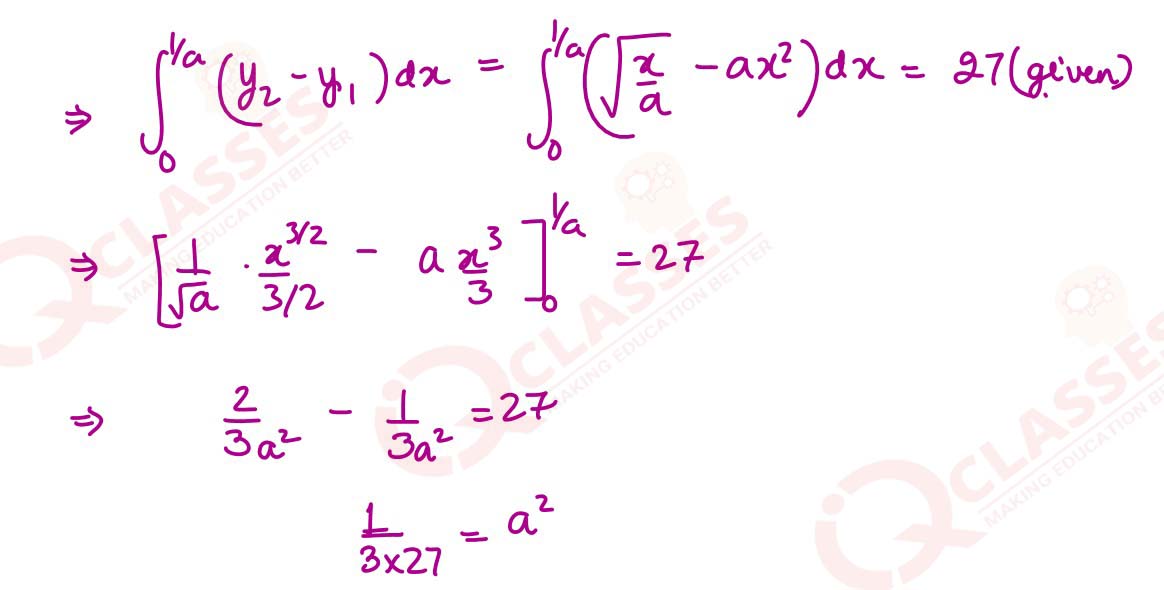
SECTION C

Question 19

In subparts (i) and (ii) choose the correct options and in subparts (iii) to (v), answer the questions as instructed.

(i) At a toy factory, the production cost per day for x number of toys is given by the following function:

C(x) = 0.0001x³- 0.01x²- 20x + 3500

Which of these represents the approximate additional cost to produce 201^st toy?

(a) C(200)
(b) AC(201)
(c) MC(200)
(d) MC(201)

(ii) At FNG High School, teachers plotted students' scores in Science and Social Studies with respect to their scores in Maths and English, from their 10th grade final examination. The graphs plotted by the teachers are shown below:

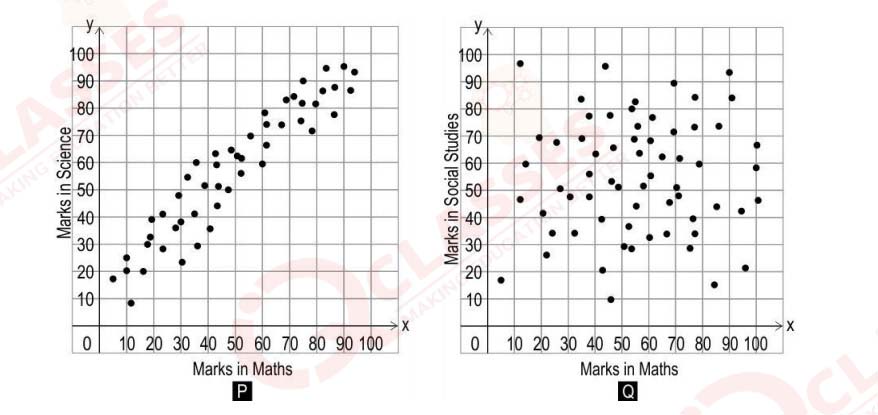
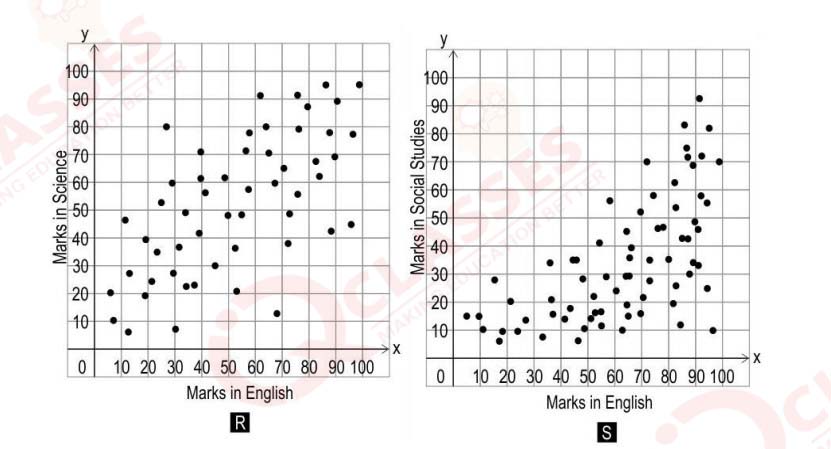
Which one of the given graphs could a line of best fit be drawn for?

(a) only P
(b) only P and S
(c) only P, R and S
(d) all P, Q, R and S

(iii) Given below are two regression lines for the same dataset.

L1: 2x = 5y - 2
L2: 3y = 2x + 1.

Identify the regression line of x on y.

(iv) The marginal revenue of a manufacturing facility is given by the function MR(x) = 408 - 17x.
The manufacturer should limit the production to 24 units. Why?

(v) Vishwanath runs a company that produces and sells a particular model of laptop. Its revenue function is given by:

R(x) = 4x³ + 1/5x² + x, where x is the number of laptops demanded and R(x) is in rupees. What is the ideal unit price (in rupees) for Vishwanath to charge for each laptop if there is a demand for 100 laptops?

Solution

Question 20

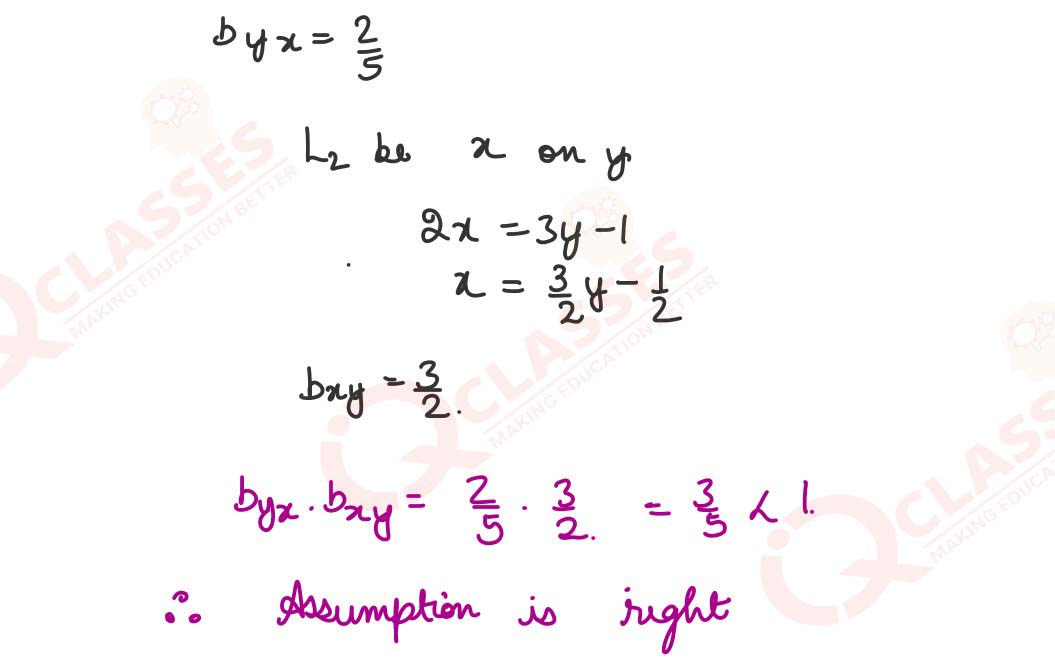
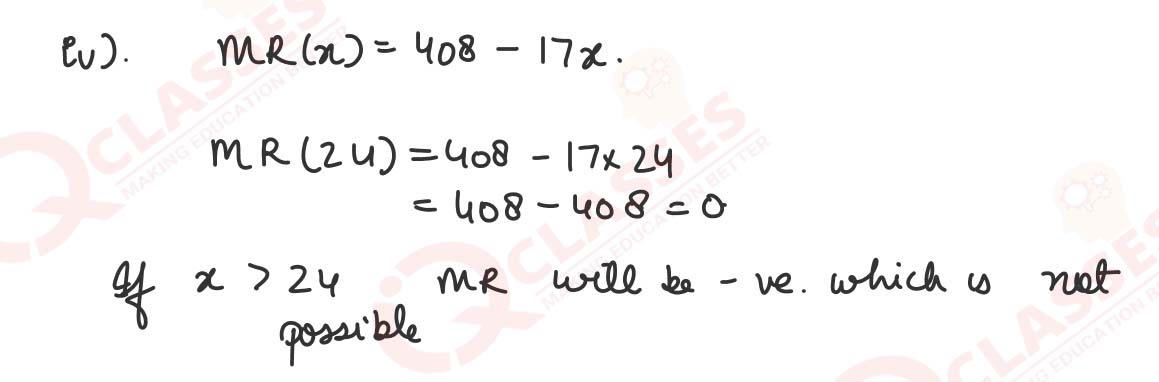
(i) A bicycle spare parts manufacturing company decided to upgrade its production unit by installing advanced machinery. As a result of this investment, the cost of producing spare parts increased. The company used to sell 1000 spare parts daily at Rs 50 per unit.

The increased daily cost of production C(x) for x number of spare parts is given by

C(x) = 99/2 x +525

If the selling price remains the same, find how many more spare parts must the company sell daily to ensure no loss.

OR

(ii) The government’s Department of Culture is organising an art and craft exhibition cum sale to promote local artists and their work. They want to charge a nominal amount as entry fee. Profit, in rupees, generated by the entry tickets can be calculated using the function: 𝑃(𝑥) = −8𝑥³+29400𝑥 − 60000 where x is the price of each ticket.

What is the ideal price for each ticket that the department should set to maximise the profit?

Solution

Question 21

Shown below is a data set that includes the average temperature and the number of ice cream cones sold per day by an ice cream truck in a small town over the course of six days.

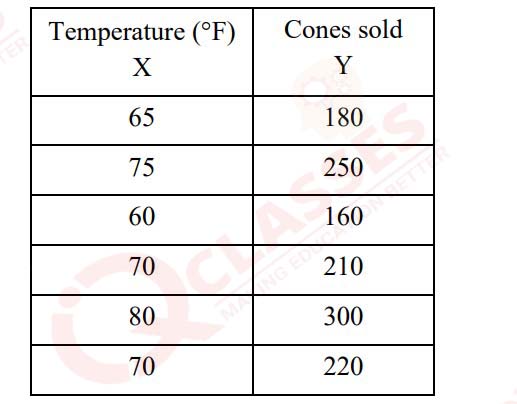
Find the line of regression using average temperature as the independent variable.

Solution

Question 22

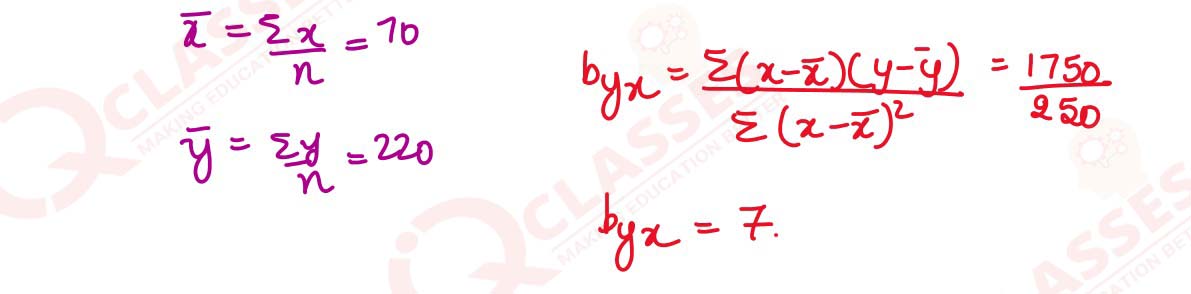
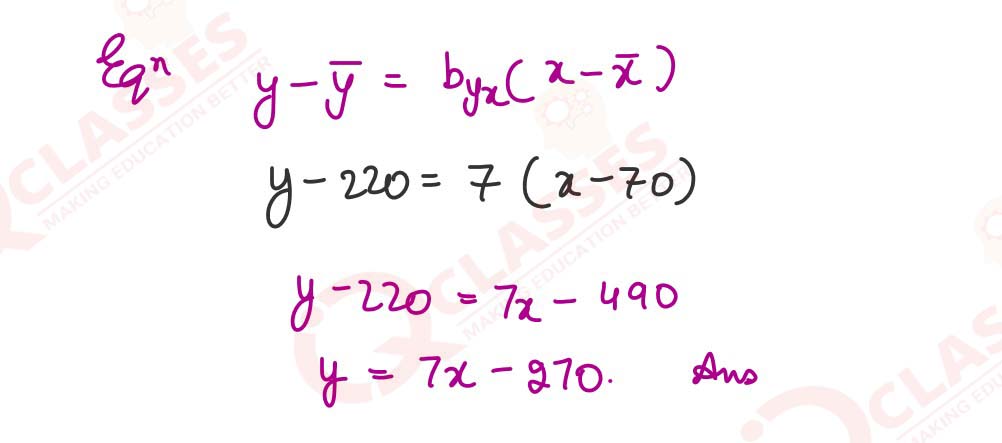
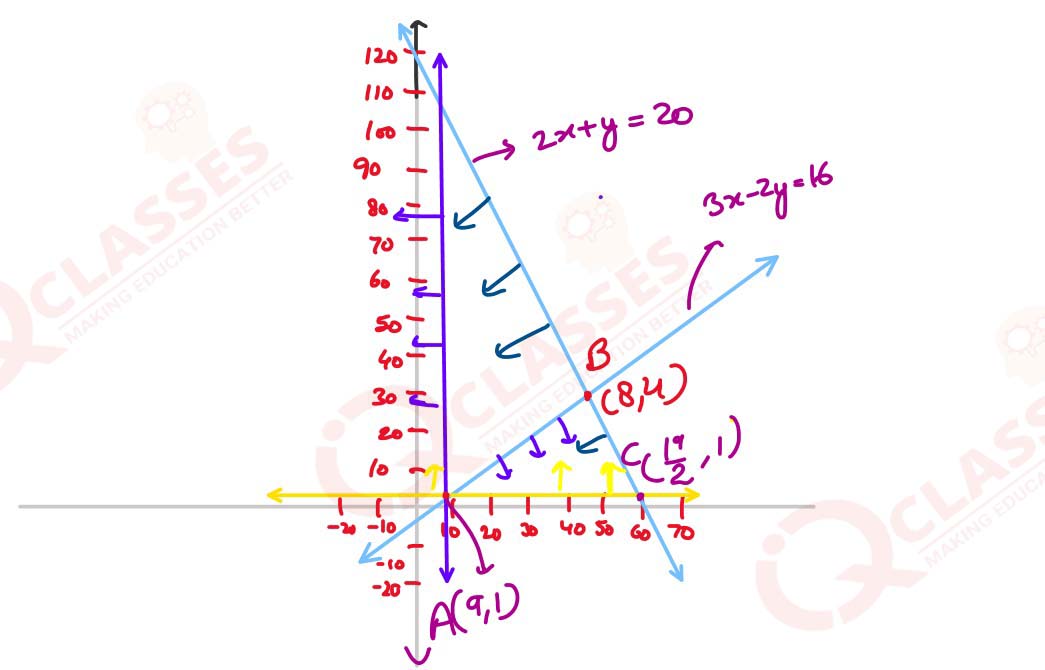
(i) Maximise Z = 4x - 3y, subject to the following constraints:

2x + y ≤ 20
3x - 2y ≥ 16
x ≤ 9
y ≥ 1

Also, find Z's maximum value.

OR

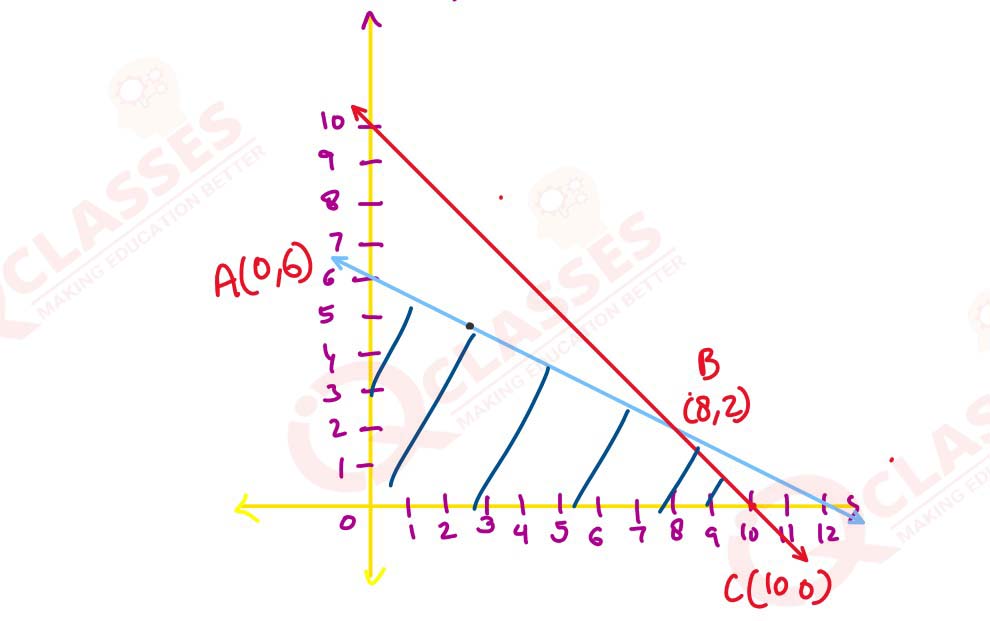
(ii) A soap company manufactures two varieties of soap using two machines. The time taken on each machine to manufacture one batch of each variety of soap is given below.

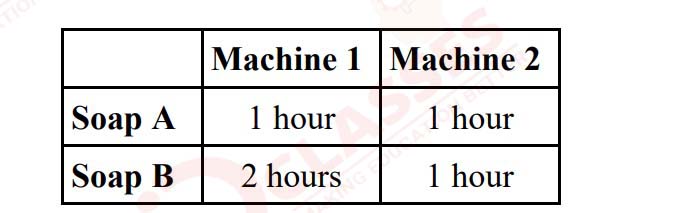
Machine 1 and Machine 2 cannot be operational for more than 12 and 10 hours in a day, respectively. The profit earned from one batch of Soap A and one batch of Soap B is ₹ 3000 and ₹ 4000, respectively.

Find the number of batches of each kind of soap that should be made daily to maximise the profit.

Class 12 ISC Maths Specimen Question Paper 2024

Section-A

Question 1 In subparts (i) to (x) choose the correct options and in subparts (xi) to (xv), answer the questions as instructed.

(i) P and Q are two matrices such that If P=,which one of the following is Q?

Solution

(ii) If ∫ sin-1(𝑐𝑜𝑠𝑥)𝑑𝑥 = 𝑔(𝑥)-x2/2 + 𝑐, then 𝑔(𝑥) will be: (a) π/2 x (b) -π/2 x (c) 0 (d) x/2

Solution

(iii) What is the value of cot (π/2 +tan-1 1/√2) (a) 1/√2 (b) π/2 (c) -1 (d) -1/√2

Solution

(iv) For what value of n is the given a homogenous differential equation? (a) 1 (b) 3 (c) 0 (d) 2

Solution

Solution

(vi) Which one of the following is equal to the above sum

Solution

(vii) Given below are the graphs of f(x) along with the statements. Which one of the following statements is NOT correct about the graphs?

Solution

Solution

Solution

Solution

(xi) The function f:X ->Y is not invertible.State the reason

Solution

(xii) If A= (5 x y 0 ) and A is symmetric, then write the relation between x and y

Solution

(xiii) If a relation 𝑅 on the set 𝐴 = {1, 2, 3} be defined by 𝑅 = {(1, 2), (2, 1)} then classify the function 𝑅.

Solution

(xiv) A company has estimated that the probabilities of success for three products introduced in the market are 1/3, 2/5 and 2/3 respectively. Assuming independence, find the probability that at least one product is successful

Solution

Solution

(i) The table below shows some of the values of differentiable functions u and v and their derivatives. If r(x) = u(v(x)), find r'(2). OR (ii) If 𝑓(𝑥) = 𝑥3 − 48𝑥, find the interval where f:R → R is decreasing

Solution

Evaluate: ∫π/2-π/2 |𝑠𝑖𝑛𝑥|𝑑x

Solution

Find the point on the curve 𝑦 = 𝑥2 + 2𝑥 − 1, where the tangent is parallel to x- axis.

Solution

(i) Evaluate: ∫ (5-3x2/6-x3+5x) dx OR (ii) Evaluate: ∫xex dx

Solution

Find the domain of the function cos-1 𝑥 + 𝑠𝑖𝑛x

Solution

Prove that cos [tan-1 {cot (sin-1x)}] = x.

Solution

Evaluate: ∫ 9x3 +63 x2/x4+14 x3-9x2 dx

Solution

(i) Shown below is a function which is differentiable at x = 3 Find the values of p and q, where they are real numbers. Show your steps and give a valid reason. OR

Solution

Solution

Solution

(i) Solve: 𝑥3𝑑𝑦 + (𝑥𝑦 − 1)𝑑𝑥 = 0. Given 𝑦 = 3 − 𝑒 𝑤ℎ𝑒𝑛 𝑥 = 1/2 find 𝑦 𝑤ℎ𝑒𝑛 𝑥 = 1 OR (ii) Evaluate: ∫ x2/x4+1 dx

Solution

Solution

Solution

SECTION B

Solution

(i) (i) Given below are two vectors in their component form such that Find the relation between the variables 𝑥 𝑎𝑛𝑑 y (ii) The position vectors of the points A and B are (2, −3, 2)and (2, 3, 1) respectively, then find the area of triangle 𝑂𝐴𝐵.

Solution

Solution

If the area enclosed between the curves 𝑦 = 𝑎𝑥2 𝑎𝑛𝑑 𝑥 = 𝑎𝑦2, 𝑎 > 0, is 27 sq. unit, find the value of 'a'

Solution

SECTION C

Solution

Solution

Shown below is a data set that includes the average temperature and the number of ice cream cones sold per day by an ice cream truck in a small town over the course of six days. Find the line of regression using average temperature as the independent variable.

Solution

Solution

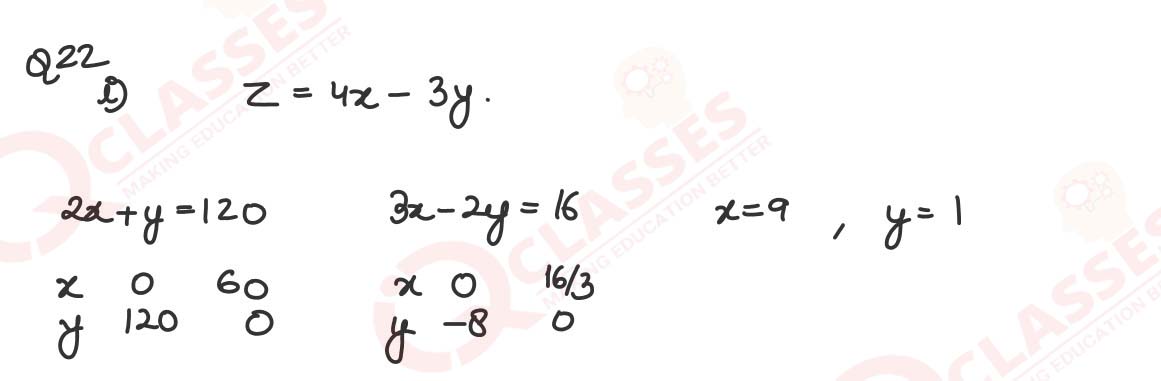
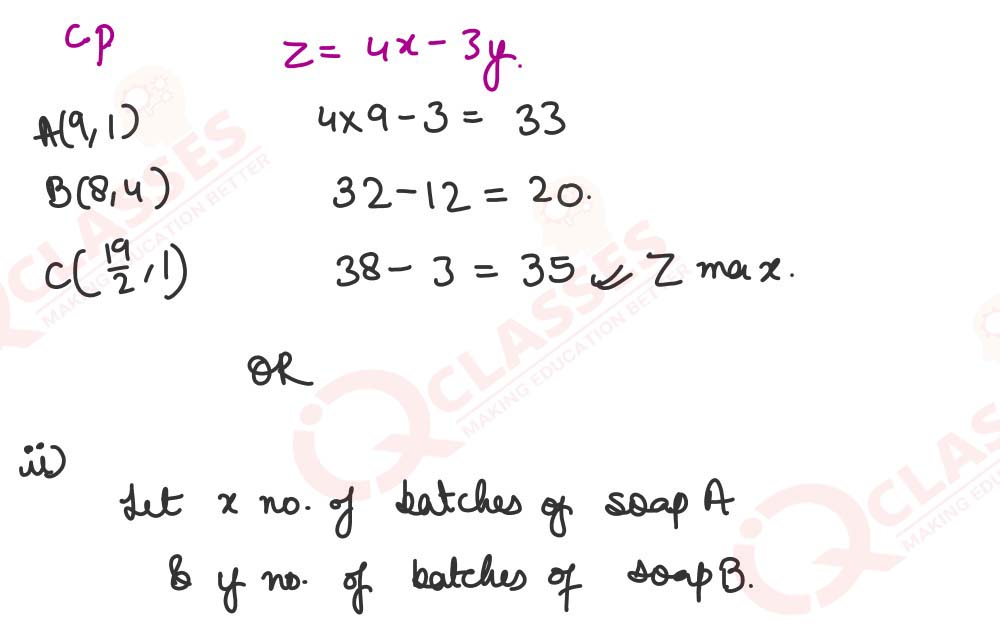
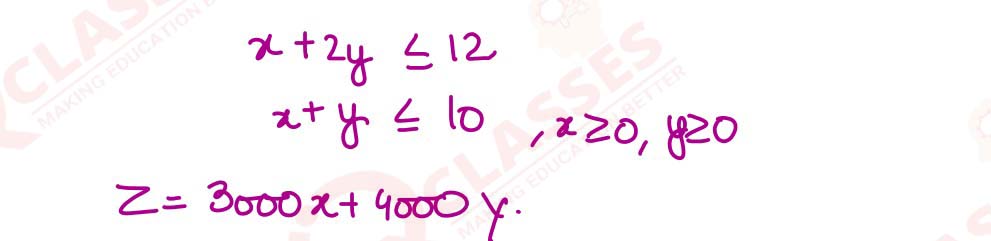
Add a comment

Reach Us

SERVICES

CONTACT

Question 1

In subparts (i) to (x) choose the correct options and in subparts (xi) to (xv), answer the questions as instructed.

(i) P and Q are two matrices such that

If P=,which one of the following is Q?

(ii) If ∫ sin^-1(𝑐𝑜𝑠𝑥)𝑑𝑥 = 𝑔(𝑥)-x²/2 + 𝑐, then 𝑔(𝑥) will be:

(a) π/2 x
(b) -π/2 x
(c) 0
(d) x/2

(iii) What is the value of cot (π/2 +tan^-1 1/√2)

(a) 1/√2
(b) π/2
(c) -1
(d) -1/√2

(iv) For what value of n is the given a homogenous differential equation?

(a) 1
(b) 3
(c) 0
(d) 2

(vi)

Which one of the following is equal to the above sum

(xii) If A=
(5 x
y 0 ) and A is symmetric, then write the relation between x and y

(i) The table below shows some of the values of differentiable functions u and v and their derivatives.

If r(x) = u(v(x)), find r'(2).

OR (ii) If 𝑓(𝑥) = 𝑥3 − 48𝑥, find the interval where f:R → R is decreasing

Evaluate: ∫^π/2_-π/2 |𝑠𝑖𝑛𝑥|𝑑x

Find the point on the curve 𝑦 = 𝑥² + 2𝑥 − 1, where the tangent is parallel to x- axis.

(i) Evaluate: ∫ (5-3x²/6-x³+5x) dx

OR

(ii) Evaluate: ∫xe^x dx

Find the domain of the function cos^-1 𝑥 + 𝑠𝑖𝑛x

Prove that cos [tan-1 {cot (sin^-1x)}] = x.

Evaluate: ∫ 9x³ +63 x²/x⁴+14 x³-9x² dx

(i) Shown below is a function which is differentiable at x = 3

Find the values of p and q, where they are real numbers. Show your steps and give a valid reason.

OR

(i) Solve: 𝑥³𝑑𝑦 + (𝑥𝑦 − 1)𝑑𝑥 = 0.

Given 𝑦 = 3 − 𝑒 𝑤ℎ𝑒𝑛 𝑥 = 1/2 find 𝑦 𝑤ℎ𝑒𝑛 𝑥 = 1

OR

(ii) Evaluate: ∫ x²/x⁴+1 dx

(i) (i) Given below are two vectors in their component form such that

Find the relation between the variables 𝑥 𝑎𝑛𝑑 y

(ii) The position vectors of the points A and B are (2, −3, 2)and (2, 3, 1) respectively, then find the area of triangle 𝑂𝐴𝐵.

If the area enclosed between the curves 𝑦 = 𝑎𝑥² 𝑎𝑛𝑑 𝑥 = 𝑎𝑦², 𝑎 > 0, is 27 sq. unit, find the value of 'a'

Shown below is a data set that includes the average temperature and the number of ice cream cones sold per day by an ice cream truck in a small town over the course of six days.

Find the line of regression using average temperature as the independent variable.