Class 12 ISC Physics Specimen 2023
Maximum Marks: 70
Time Allowed: Three hours
(Candidates are allowed additional 15 minutes for only reading the paper.
They must NOT start writing during this time).
This paper is divided into four sections – A, B, C and D.
Answer all questions.
Section A consists of one question having sub-parts of one mark each.
Section B consists of seven questions of two marks each.
Section C consists of nine questions of three marks each, and
Section D consists of three questions of five marks each
.
Internal choices have been provided in two questions each in Section B,
Section C and Section D.
The intended marks for questions are given in brackets [ ].
All working, including rough work, should be done on the same sheet as and
adjacent to the rest of the answer.
Answers to sub parts of the same question must be given in one place only.
A list of useful physical constants is given at the end of this paper.
A simple scientific calculator without a programmable memory may be used for
calculations.
Section-A
Question
1
A. In questions (i) to (vii) below, choose the correct alternative (a), (b), (c) or (d) for each of the questions given below:
(i) The surface charge density of a large conducting sheet is 17·7 ×
10-6Cm-2
.
The electric field intensity at a point outside the sheet but close to it is:
(a) 1×104 NC-1
(b) 5×104 NC-1
(c) 1×105 NC-1
(d) 1×106 NC-1
Solution
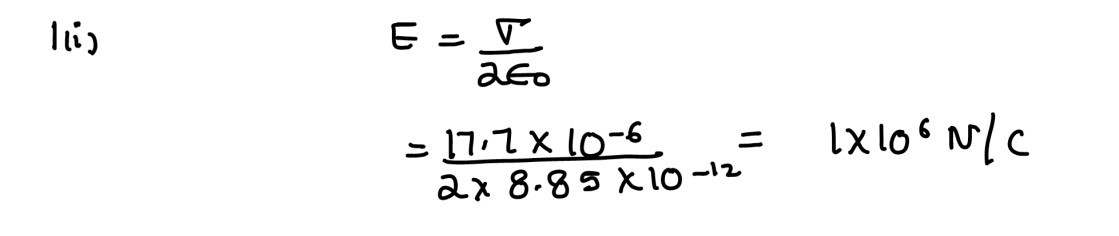
(ii) If R1 and R2 are filament resistances of a 100W bulb and
a 50W bulb
respectively, designed to operate on the same voltage, then:
(a) R1 = R2
(b) R1 = 4R2
(c) R2 = 4R1
(d) R2 = 2R1
Solution

(iii) Magnetic flux density (B) of the magnetic field at a point on the axis of a
long straight solenoid is given by:
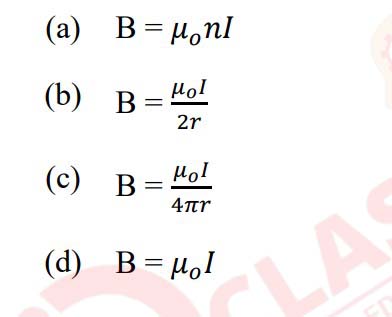
Solution

(iv) Two thin lenses having optical powers of -8D and +12D are placed in contact
with each other. The focal length of this combination is:
(a) + 0·25 m
(b) - 0·25 m
(c) + 0·25 cm
(d) - 0·25 cm
Solution

(v) Cylindrical wavefronts are produced by:
(a) a point source of light
(b) a line source of light
(c) a source at infinity
(d) all types of sources of light
Solution
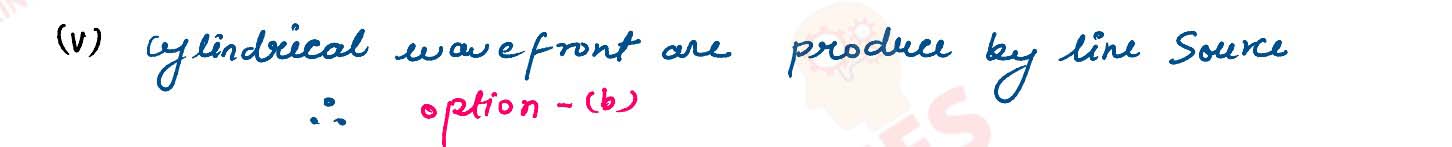
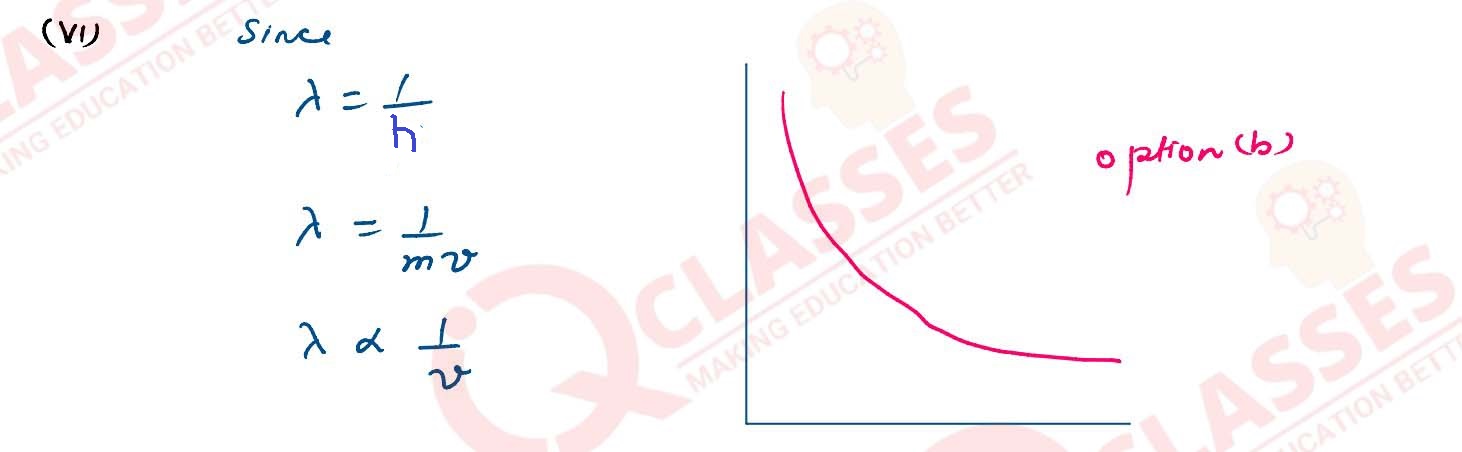
(vi) The graph of de-Broglie wavelength (λ) of a moving electron versus its
velocity (v) is:
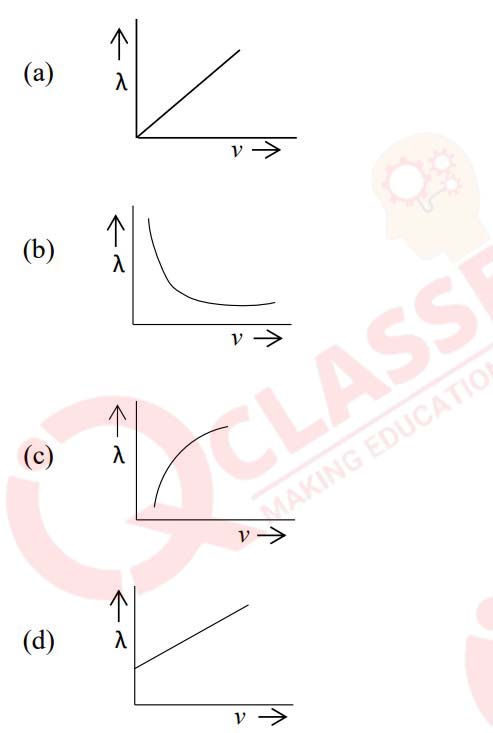
Solution
(vii) ‘n’ type semiconductor is that which has
(a) holes as majority carriers.
(b) free electrons as majority carriers.
(c) holes and free electrons equal in number.
(d) trivalent element as an impurity
Solution

(B) Answer the following questions briefly:
(i) In an electric dipole, what is the locus of a point having zero potential?
(ii) Name the conservation principle implied in Kirchhoff’s Junction law for
electric circuits.
(iii) Give any one reason why efficiency of a transformer is always less than 1.
(iv) Give an example of coherent sources of light.
(v) In Young’s double slit experiment, what is the path difference between the
two light waves forming 5th bright fringe on the screen?
(vi) State the function of a moderator in a nuclear reactor.
(vii) In semiconductors, what is meant by “doping”?
Solution





Section-B
Question 2
(i) You are provided with many identical capacitors each of capacitance 100μF.
How will you connect a minimum number of them to obtain a capacitance of 75μF?
Draw a diagram in support of your answer.
OR
(ii) Three point charges of 50nC each are kept at the vertices of an equilateral triangle
having each side = 3m. Calculate electrostatic potential energy of the system
Solution
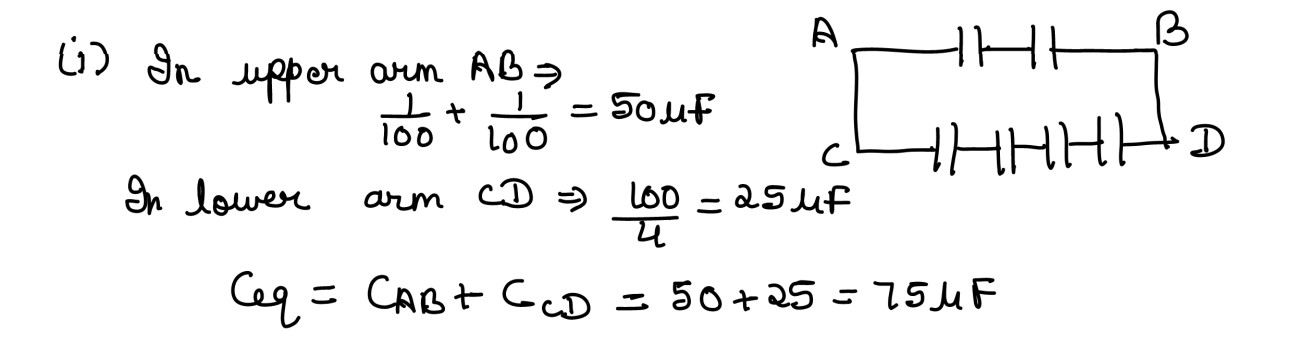
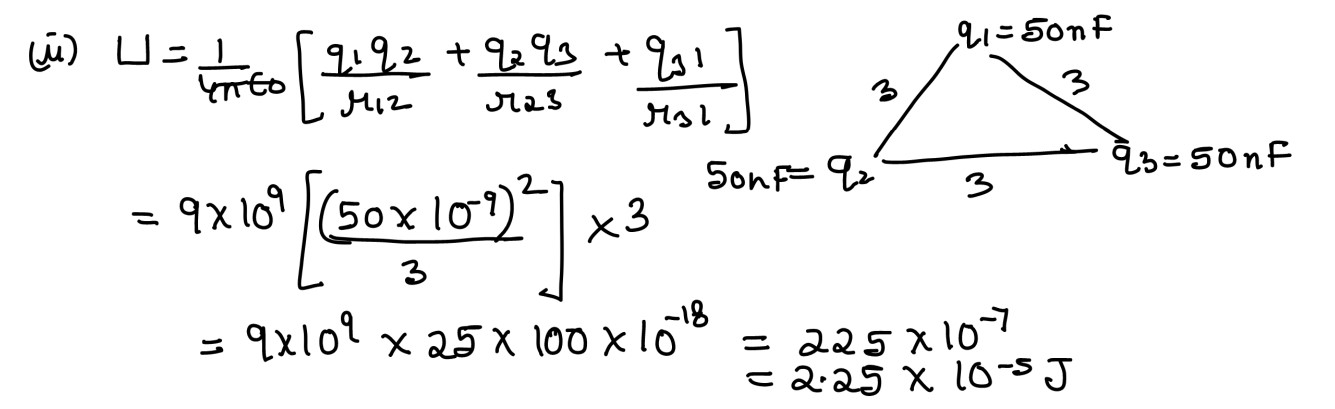

Question 3
(i) With reference to free electron theory of conductors, define:
(a) Drift velocity
(b) State any one use of a potentiometer.
Solution

Question 4
Explain why a blue coloured spark is often seen in a switch when a circuit containing an electric iron/geyser is switched off.
Solution
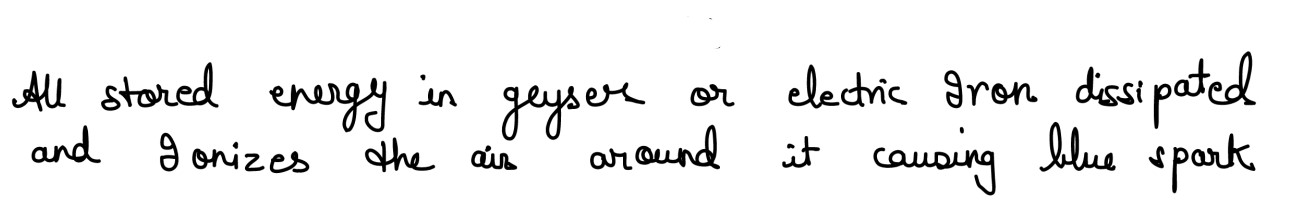
Question 5
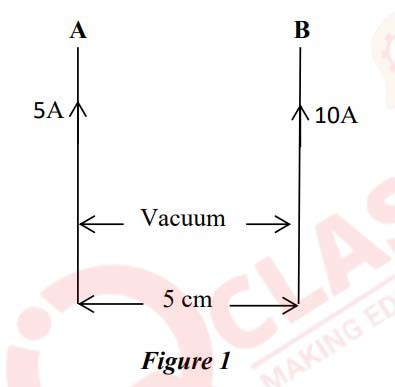
(i) Two long straight wires A and B are kept parallel to each other, 5 cm apart, in
vacuum. They carry currents of 5A and 10A respectively in the same direction as
shown in Figure 1 below. Calculate the force per unit length acting on the wire B
due to the current flowing in the wire A.
OR
(ii) An electron moving with a velocity of 8 × 106
m/s enters a uniform and transverse
magnetic field of 3 × 10-3T. Calculate the radius of the circular path described by it.
Solution
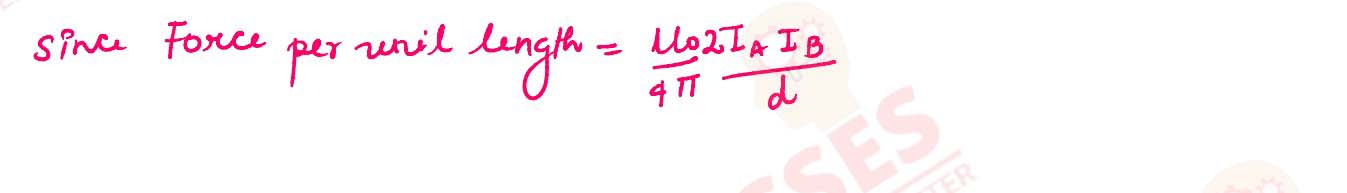
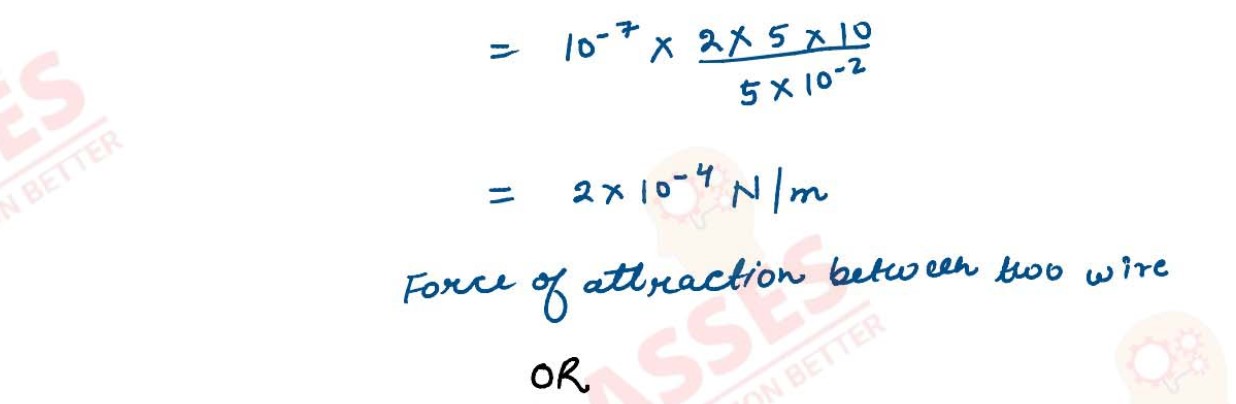
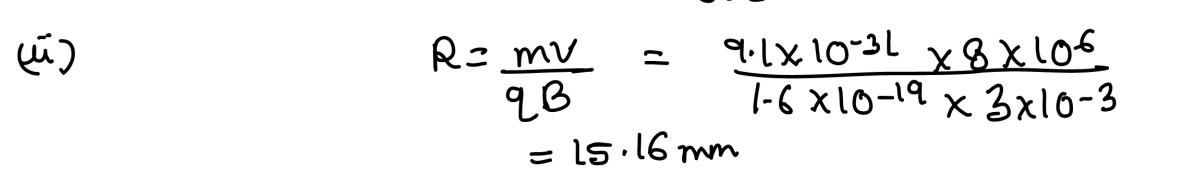
Question 6
Name the electromagnetic radiation:
(i) used for viewing through haze and fog.
(ii) which has the wavelength of 0·1 nm.
Solution

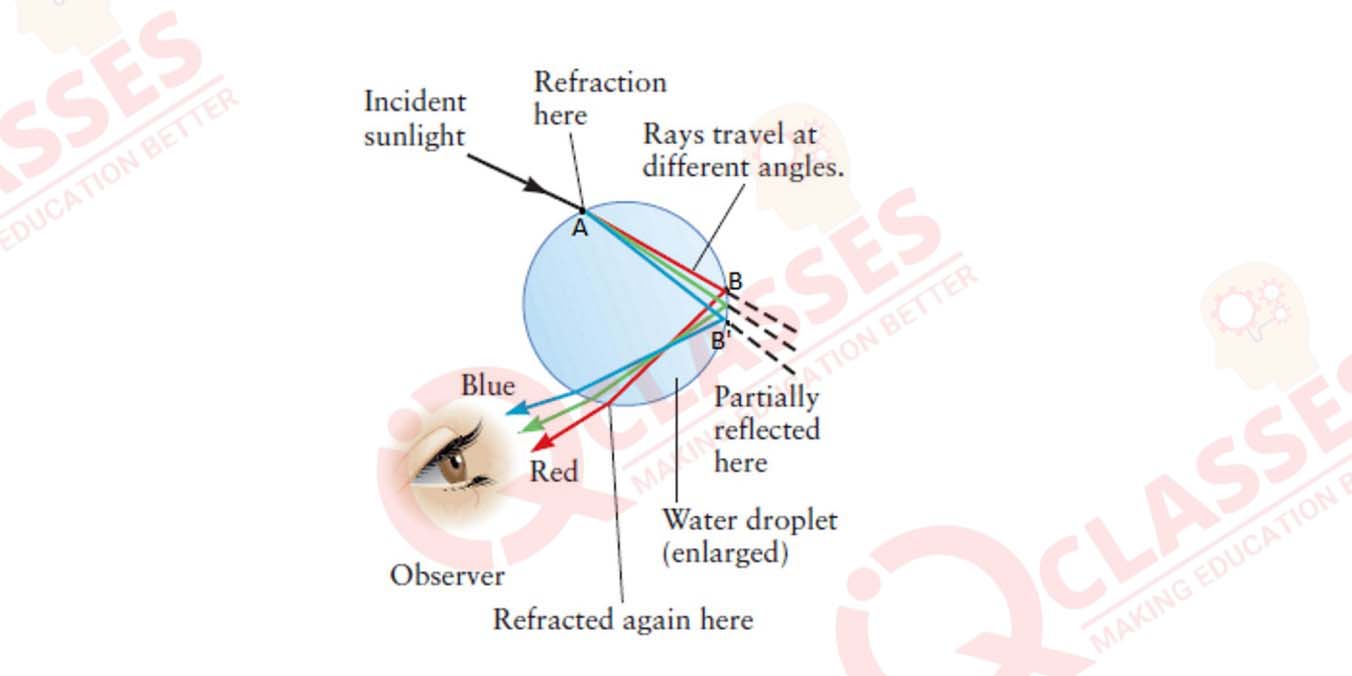
Question 7
Draw a neat and labelled ray diagram to show the formation of a primary rainbow
Solution
Question 8
With reference to a semiconductor diode, explain the terms:
(i) Depletion region
(ii) Potential barrier or barrier p.d.
Solution

Section-C
Question 9
Obtain an expression for intensity of electric field at a point in end on position i.e. on an axial line of an electric dipole.
Solution




Question 10
(i) In a meter bridge circuit, resistance in the left gap is 4Ω and an unknown
resistance
R is in the right-hand gap as shown in Figure 2 below. The null point is found to
be 40 cm from the left end of the wire.
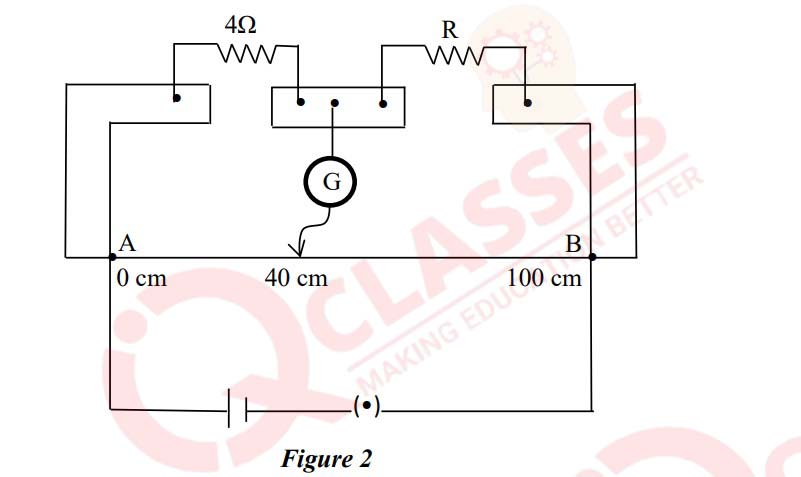
(a) Calculate the value of the unknown resistance R.
(b) What change will you make in R to bring the null point to the midpoint of the
wire AB?
OR
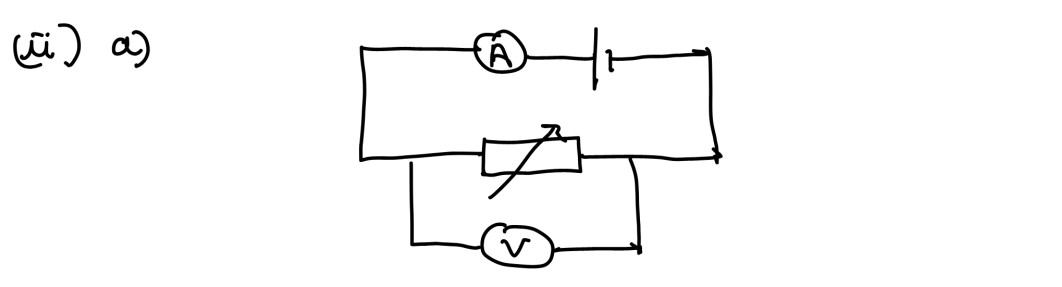
(ii) A circuit is used to determine the internal resistance and the emf of a cell. It consists
of the cell, a variable resistor, an ideal ammeter A and an ideal voltmeter V.
Figure 3 shows part of the circuit with the ammeter and voltmeter missing.
The variable resistor is set to be 1·5Ω. When the cell converts 7·2mJ of energy.,
5·8mC of charge moves completely around the circuit. The potential difference
across the variable resistor is 0·55V.
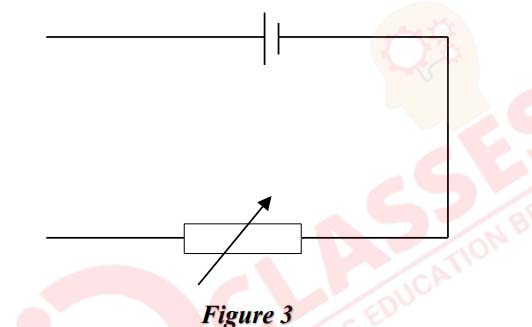
(a) Redraw the diagram showing the positions of the ammeter and the voltmeter.
(b) Calculate the emf of the cell.
Solution

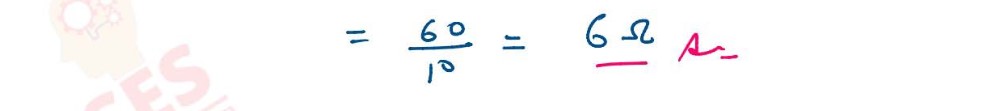
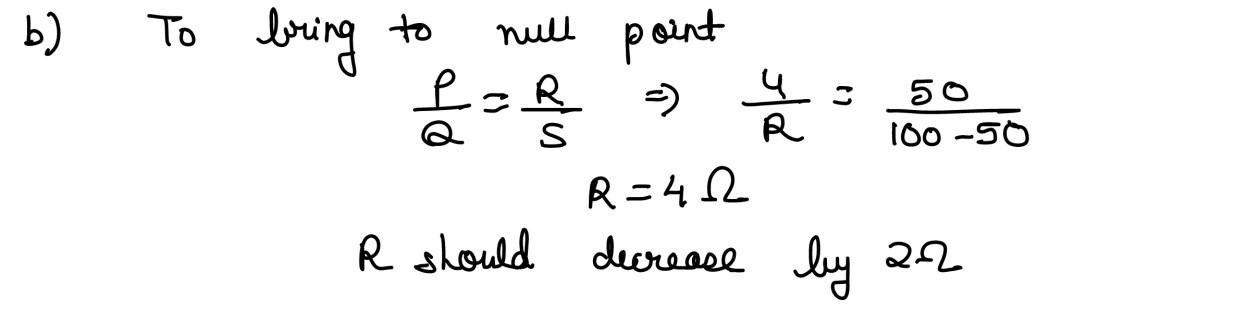

Question 11
Obtain an expression for magnetic flux density B at the centre of a current carrying circular coil.
Solution


Question 12
Using Huygen's wave theory, prove Snell's law of refraction of light
Solution



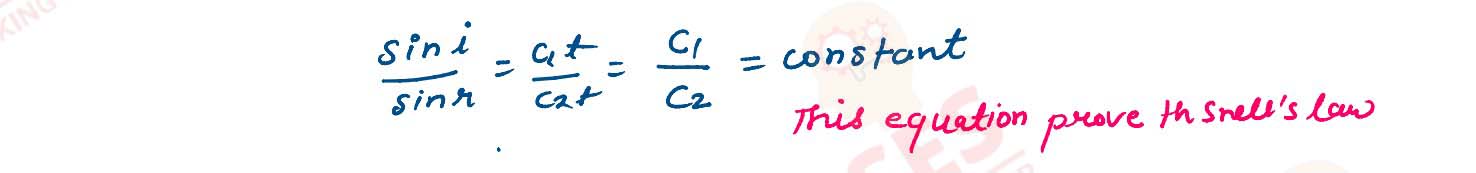
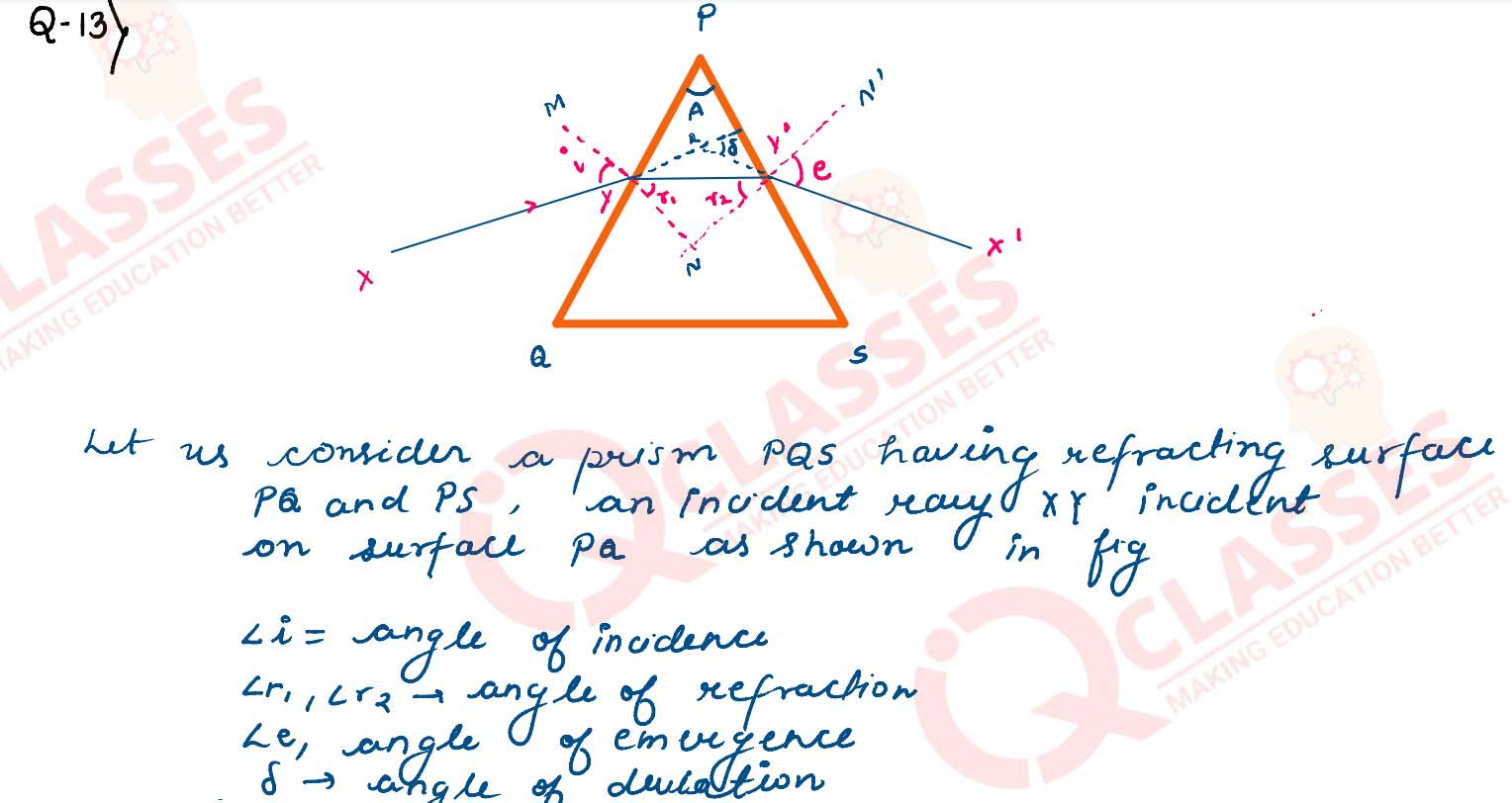
Question 13
(i) Obtain Prism formula i.e. prove that
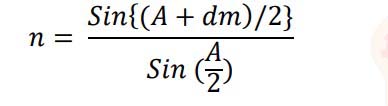
Where the terms have their usual meaning.
OR
(ii) Derive Lens Maker’s formula.
Solution





Question 14
(i) Calculate the angular width of the central maxima obtained in Fraunhofer single
slit diffraction experiment, when a monochromatic light of wavelength 550 nm
falls normally on a rectangular slit of width 1·1×10-4
cm.
(ii) How will its value change if the experiment is repeated with monochromatic light
of greater wavelength?
Solution
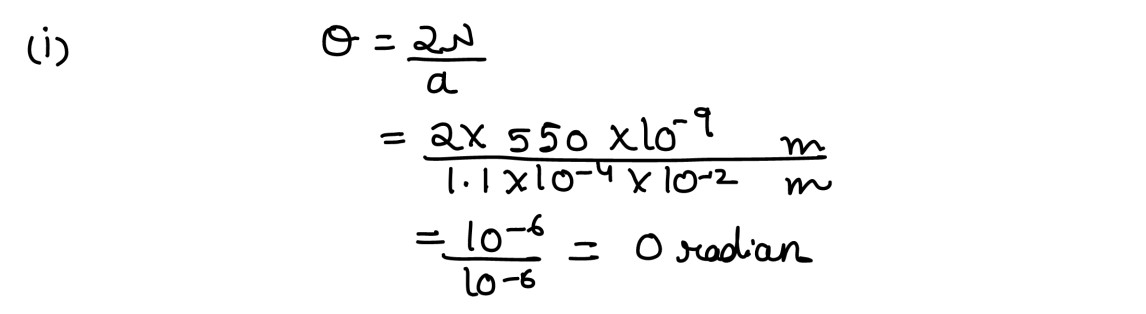

Question 15
(i) With reference to photoelectric effect, plot a labelled graph of stopping
potential
(Vs) versus frequency (f)of the incident radiation.
(ii) State how will you use this graph to determine the value of Planck’s constant.
Solution

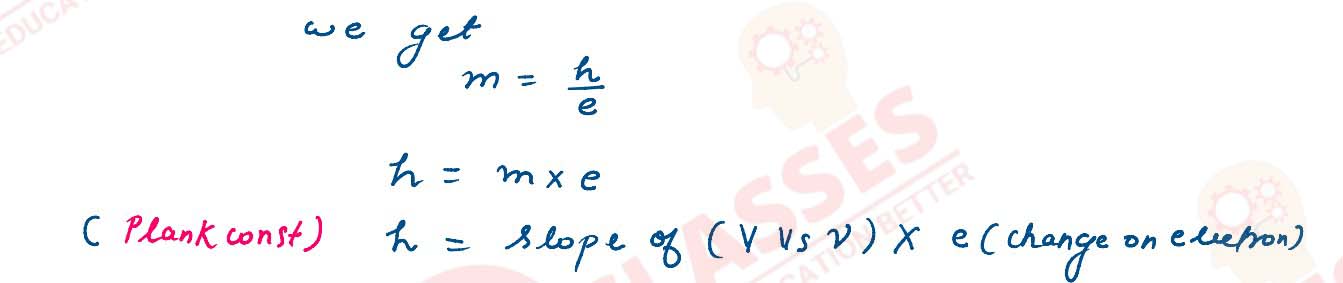
Question 16
(i) State any two differences between Nuclear fusion and Nuclear fission.
(ii) What is the essential difference between the working of a fission bomb and a
nuclear reactor?
Solution

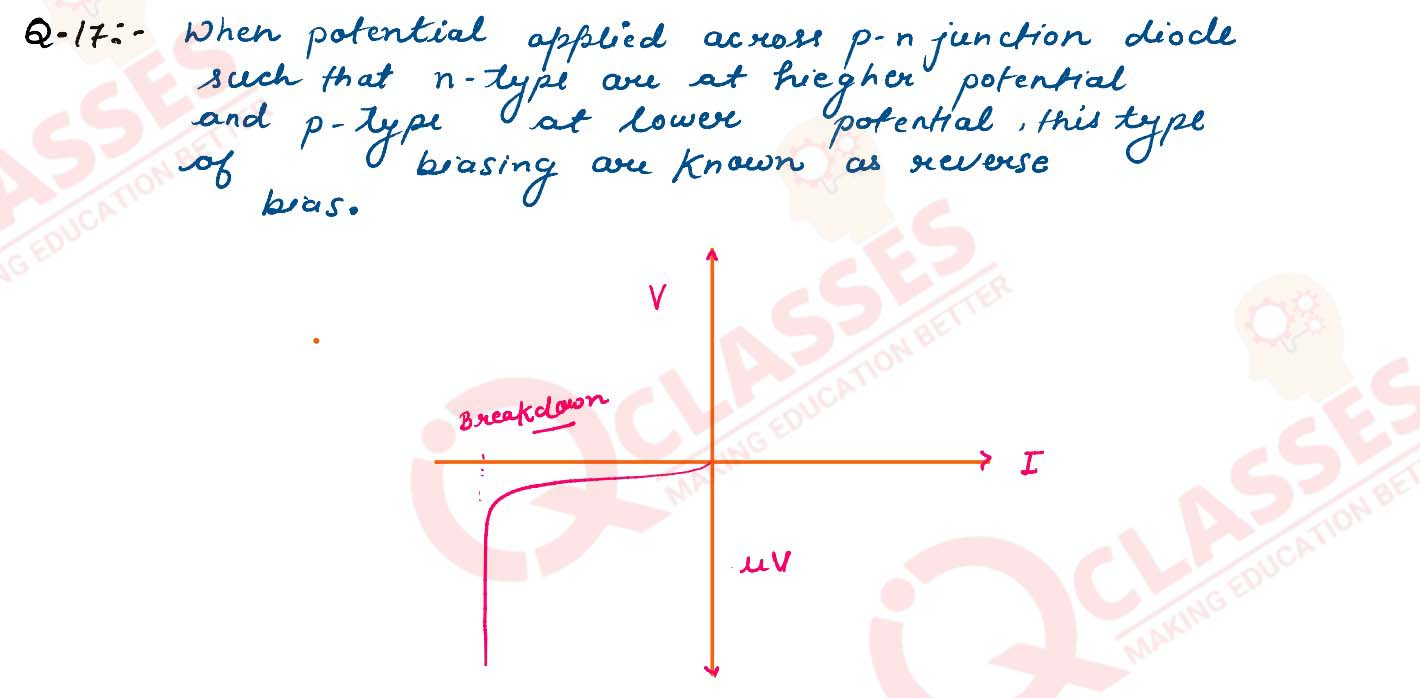
Question 17
What is meant by reverse biasing of a semiconductor diode? Draw a labelled characteristic curve i.e. I - V graph for a semiconductor diode during reverse bias.
Solution
Section-D
Question 18
(i) An 80Ω resistor, a 1·0 H inductor and a 40 𝜇F capacitor are connected in
series to
an a.c. supply of 220V such that the circuit draws the maximum current. At this
stage, calculate:
(a) Resonant frequency of the circuit.
(b) Capacitive reactance of the circuit.
(c) Impedance of the circuit
(d) Current flowing through the circuit.
(e) Phase difference between capacitive and inductive voltages.
OR
(ii) Figure 4 below shows two thick metallic rails CD and GH kept parallel to each
other 0·8m apart. They are joined to each other by a resistance wire R having a
resistance of 5Ω. A thick metallic rod PQ rests on the rails. There is a uniform
magnetic field B = 0·2T, which is perpendicular to the plane of the rails, pointing
into the paper.
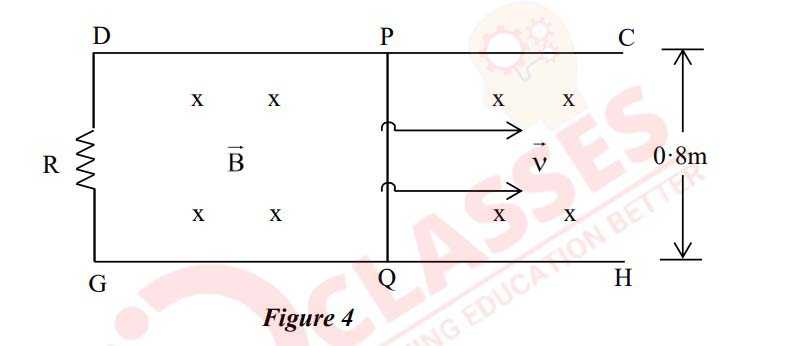
(a) Calculate magnitude and direction of the current induced in the rod PQ if it is
moved towards right with a constant velocity v = 36 km/hr.
(b) The rod PQ is now made to perform simple harmonic motion with a
frequency of 3Hz and an amplitude of 4cm. Calculate the maximum value of
the emf induced in the rod.
Solution
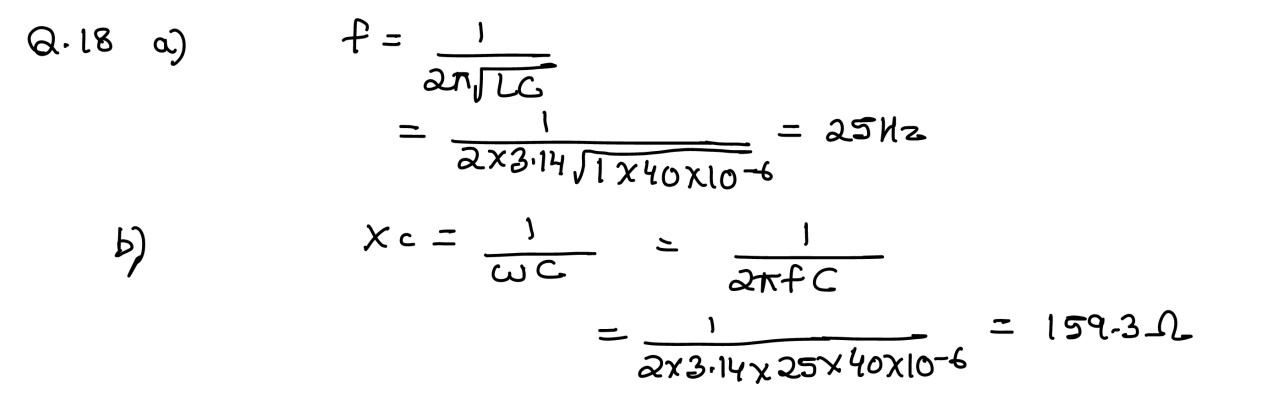
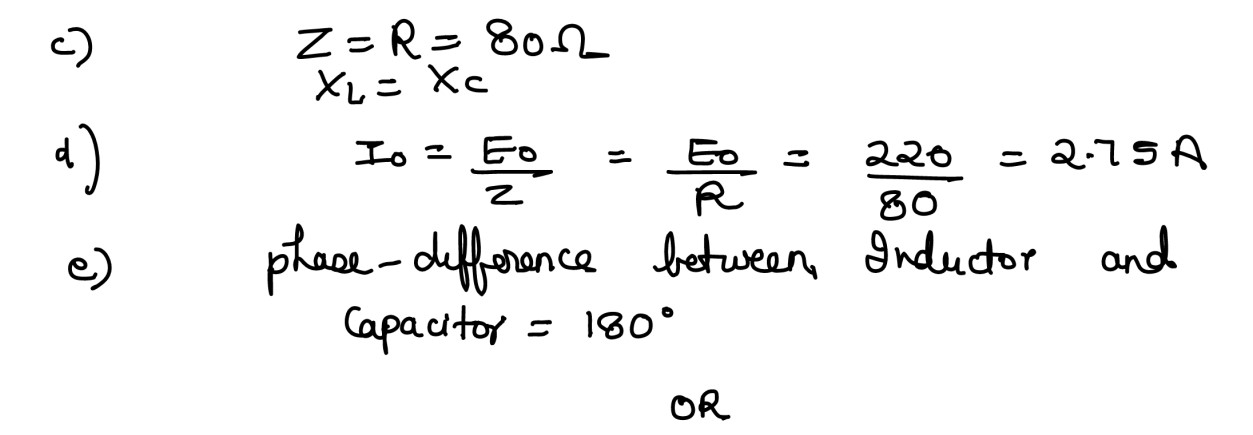
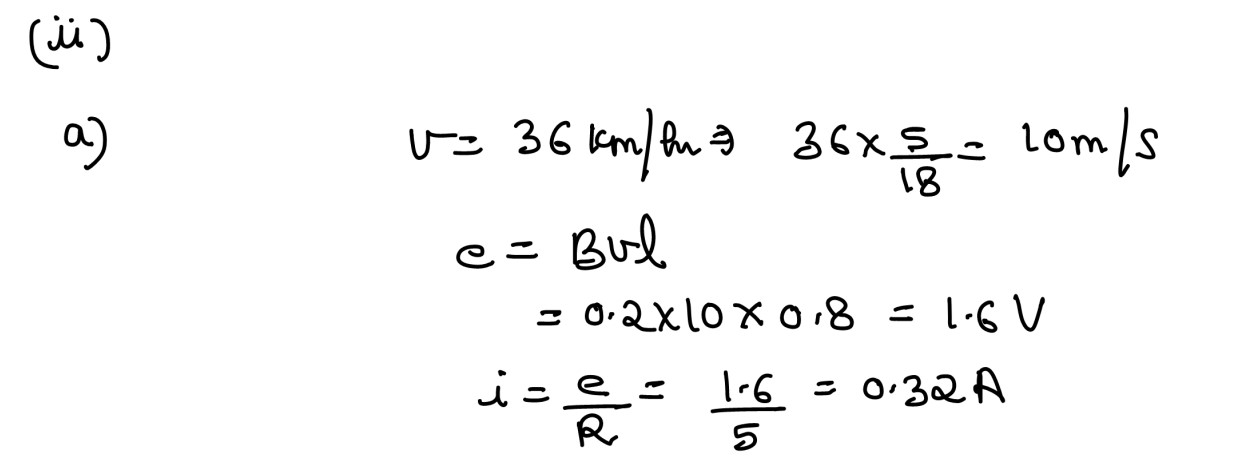



Question 19
(i) (a) Using Bohr’s theory of hydrogen atom, obtain an expression for the radius
of
the nth orbit of an electron in an atom.
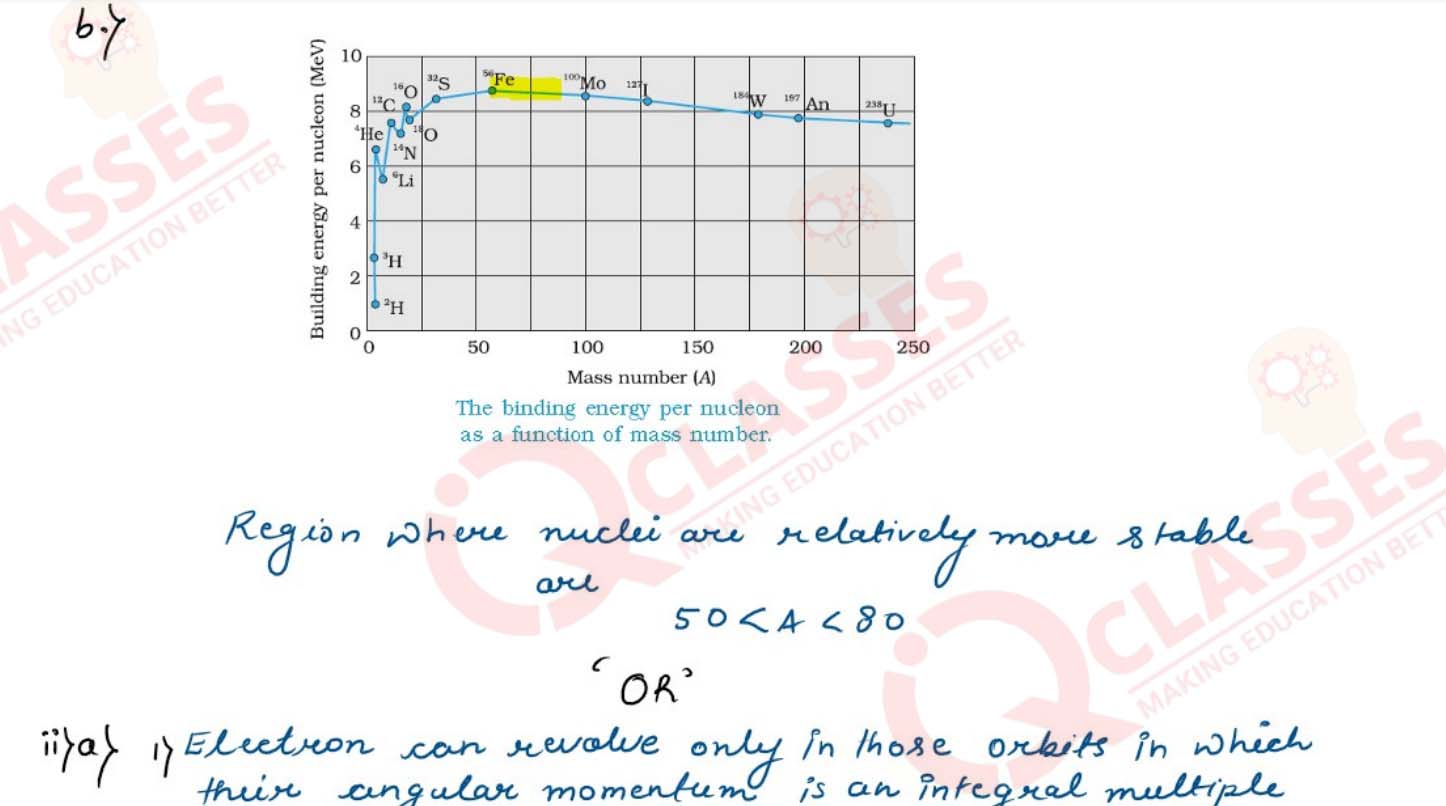
(b) Draw a labelled graph of binding energy of a nucleus per nucleon versus its
mass number. Mark the region where nuclei are relatively more stable.
OR
(ii) (a) State the postulate of Bohr’s theory regarding
(1) Quantisation of angular momentum of an electron.
(2) Emission of energy by an atom.
(b) What is meant by the following terms?
(1) Mass defect of a nucleus.
(2) Binding energy of a nucleus.
State how these two are related to each other.
Solution

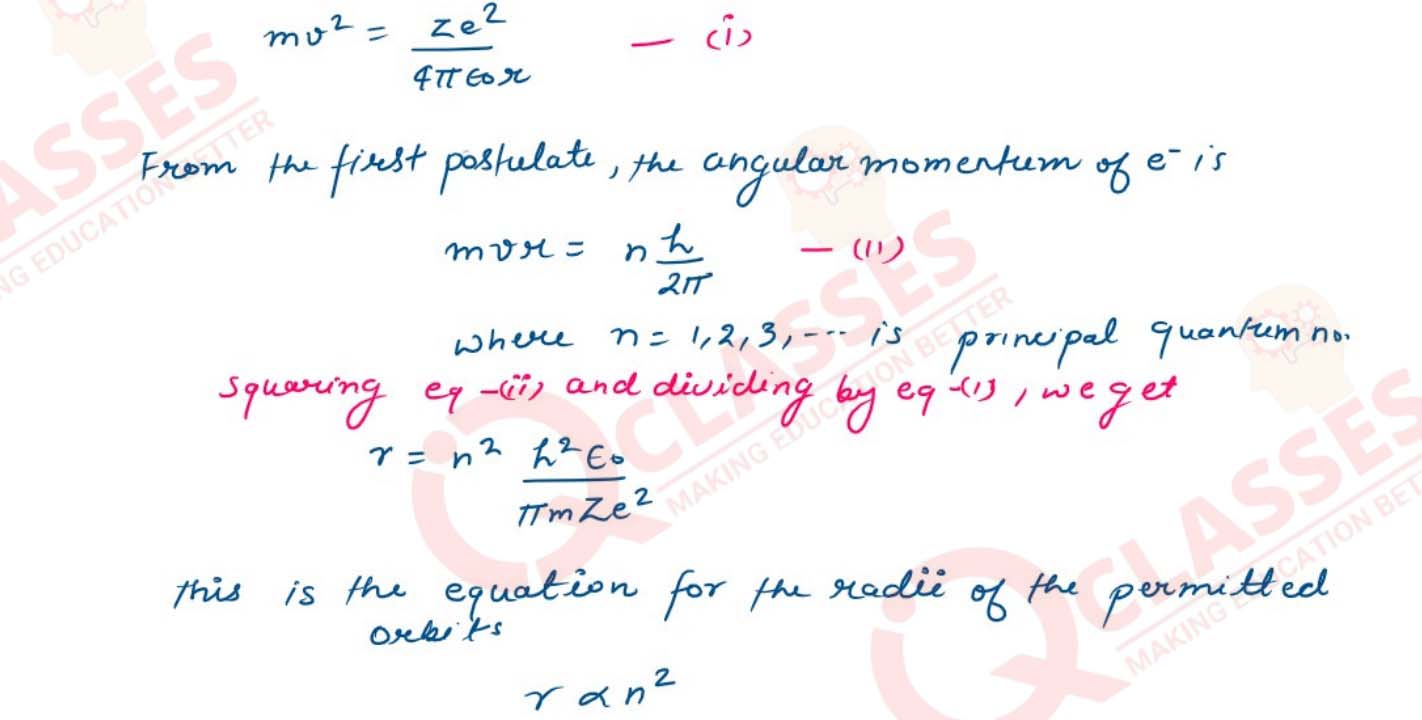



Question 20
Read the passage given below and answer the questions that follow.
Optical instruments are of great utility. They help us in studying very tiny objects as well
as very large heavenly bodies. Scientists have developed microscopes like electron
microscopes which aid in studying tiny molecules of matter. They have also devised giant
telescopes like Hubble telescope and James Web Space telescope which have enabled us to
view distant galaxies hitherto unknown.
(i) Which optical instrument is used to study detailed structure of a virus?
(ii) What is the ability of an instrument to form an enlarged image of an object called?
(iii) Hubble telescope orbits around the earth like a satellite. What is the advantage of
such a telescope over a similar one on earth’s surface?
(iv) An astronomical telescope consists of two convex lenses having focal length of
200cm and 4cm. When it forms final image at infinity, calculate its
(a) Magnifying power
(b) Length.
Solution


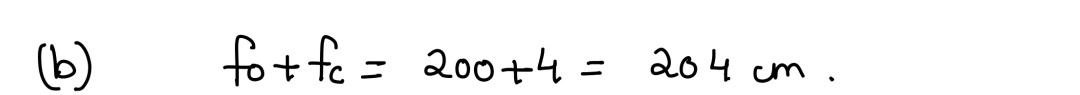

Add a comment