Class 12 ISC Term1 Maths Specimen 2022

Question 1 [Mathematics Specimen Paper Term-I 2021]

Q.1 (1) The function f: R → R defined by 𝑓(𝑥) = 𝑠𝑖𝑛 (3𝑥 + 2), ∀ 𝑥 ∈ 𝑅 is

1. One-One
2. Onto
3. Neither one-one nor onto
4. one-one but not onto

Solution

(2) What will be the Principal value of 𝐶𝑜𝑠𝑒𝑐−1 (−√2)?

1. 3𝜋/4
2. −𝜋/6
3. 𝜋/4
4. -𝜋/4

Solution

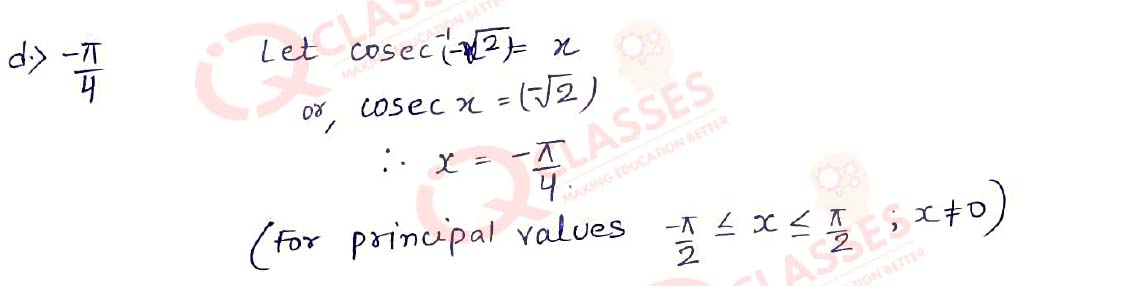
(3) If set A contains 5 elements and set B contains 6 elements, then the number of one-one onto mappings from A to B is.

1. 720
2. 120
3. 0
4. none of the above

Solution

(4) If 𝛼 ≤ 2𝑆𝑖𝑛−1𝑥 + 𝐶𝑜𝑠−1𝑥 ≤ 𝛽, then (𝛼, 𝛽) is.

1. (0, 𝜋)
2. (−𝜋/2,𝜋/2)
3. (−3𝜋/2,𝜋/2)
4. None of the above

Solution

(5) Let A be the set of all students of a boy’s school. Then the relation R in A is defined by:
R = {(a,b) : a is sister of b} is .

1. an equivalence relation
2. symmetric relation
3. an empty relation
4. a universal relation

Solution

(6) ∀ 𝑥 ∈ 𝑅, 𝐶𝑜𝑡^-1(−𝑥)=

1. 𝜋 − 𝑐𝑜𝑡^-1x
2. −𝑡𝑎𝑛^-1 𝑥
3. −𝑐𝑜𝑡^-1x
4. 𝜋 + 𝑐𝑜𝑡^-1x

Solution

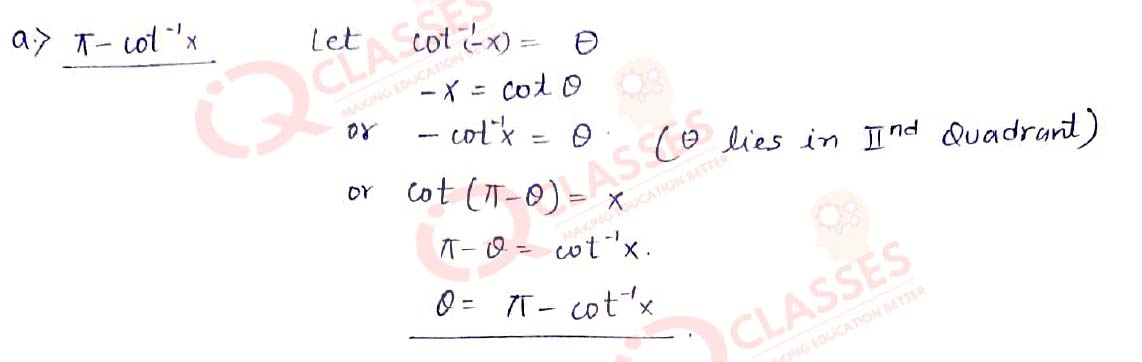
(7) The value of |1 log_ab|
                           |𝑏log_b𝑎 1| is:

1. 1 − log 𝑎b
2. 1 −log 𝑏/loga
3. 0
4. log 𝑎𝑏 − 1

Solution

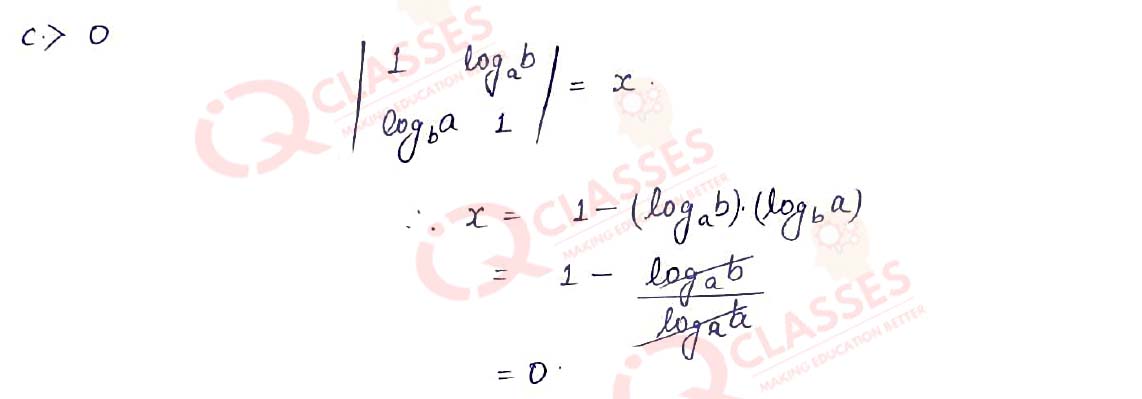
(8) From the matrix equation 𝐴𝐵 = 𝐴𝐶, it can be concluded that 𝐵 = 𝐶 provided.

1. 𝐴 is singular matrix
2. 𝐴 is non-singular matrix
3. 𝐴 is a symmetric matrix
4. 𝐴 is a skew symmetric matrix

Solution

(9) What is the transpose of a column matrix?

1. Zero matrix
2. Diagonal matrix
3. Column matrix
4. Row matrix

Solution

(10) What is the multiplicative inverse of matrix 𝐴 is?

1. 𝐴
2. A²
3. |𝐴|
4. 𝑎𝑑𝑗𝐴/|𝐴|

Solution

(11) If 𝐴 and 𝐵 are two non singular matrices, and 𝐴𝐵 exists, then (𝐴𝐵)^-1 is.

1. 𝐴^-1𝐵^-1
2. B^-1A^-1
3. 𝐴𝐵
4. None of the above

Solution

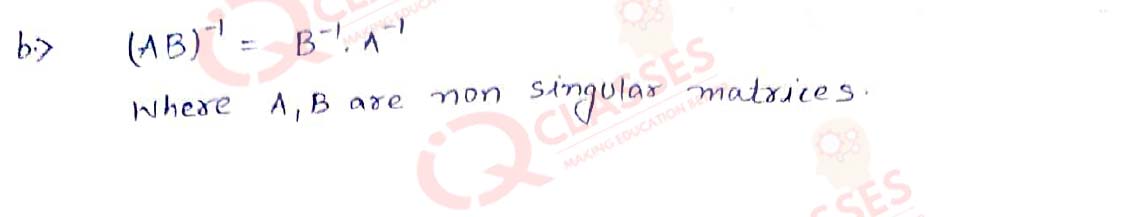
(13) If 𝑦 = 𝑡² and t = x + 3 then 𝑑𝑦/𝑑𝑥 is equal to

1. (𝑥 + 3)²
2. 2(𝑥 + 3)
3. 2𝑡
4. 2(𝑥 + 3)²

Solution

(14) The set of points, where the function 𝑓(𝑥) = 𝑥 |𝑥| is differentiable in.

1. (−∞, ∞)
2. (−∞, 0) ∪ (0, ∞)
3. (0, ∞)
4. [0, ∞ )

Solution

(15) If sin^-1 𝑥 + sin^-1𝑦 =𝜋/2, then 𝑑𝑦/𝑑𝑥 is equal to

1. x/y
2. -x/y
3. y/x
4. -y/x

Solution

(16) The value of lims_x-.0log(1+𝑥)/𝑥 is equal to

1. e
2. 0
3. 1
4. -1

Solution

(17) What will be the value of x for the determinant equation =0

1. 6
2. 3
3. 0
4. -6

Solution

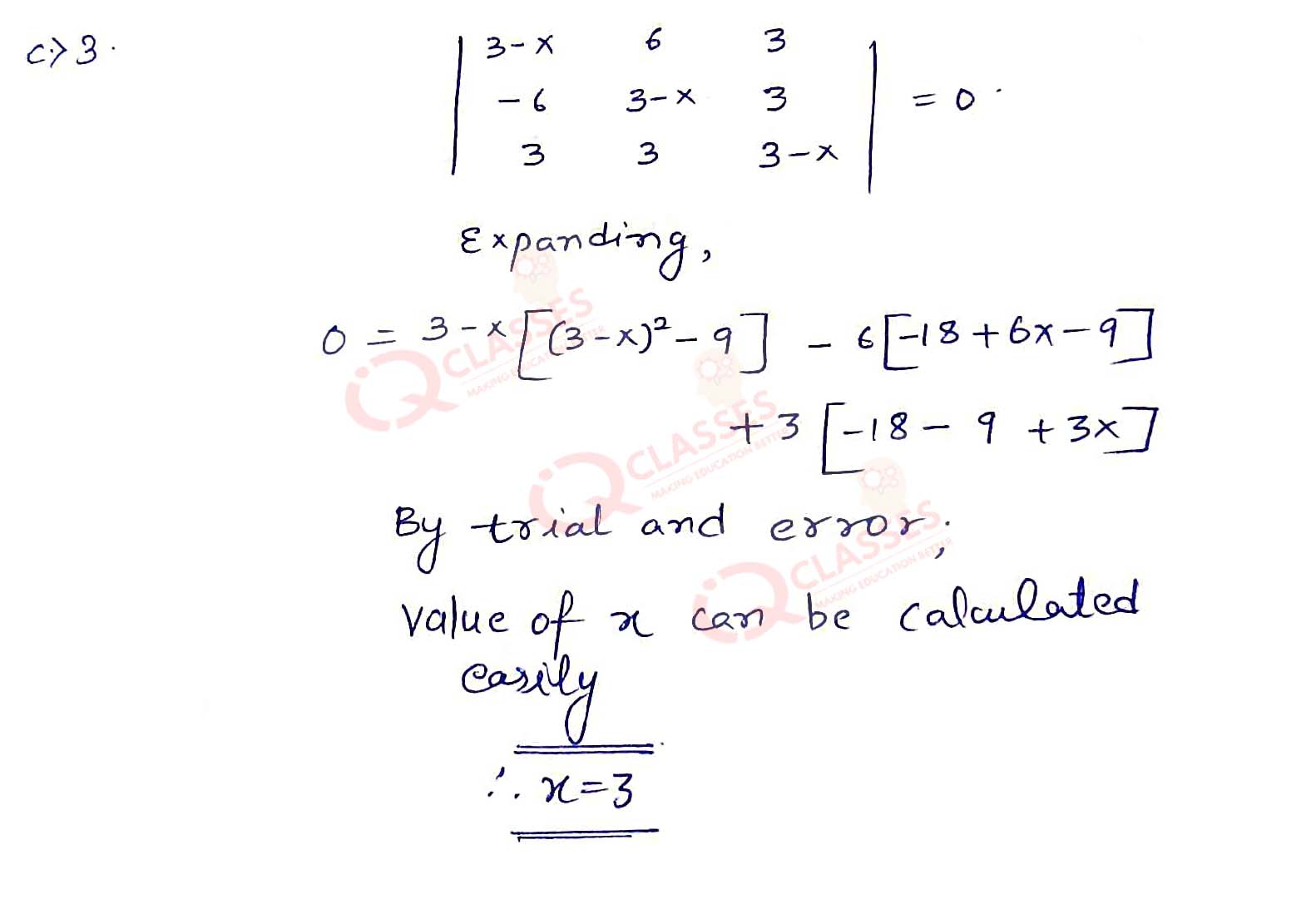
(18) Any tangent to the curve 𝑦 = 3𝑥⁷ + 5𝑥 + 3 :

1. is parallel to x – axis
2. is parallel to y – axis
3. makes an acute angle with x – axis
4. makes on obtuse angle with y – axis

Solution

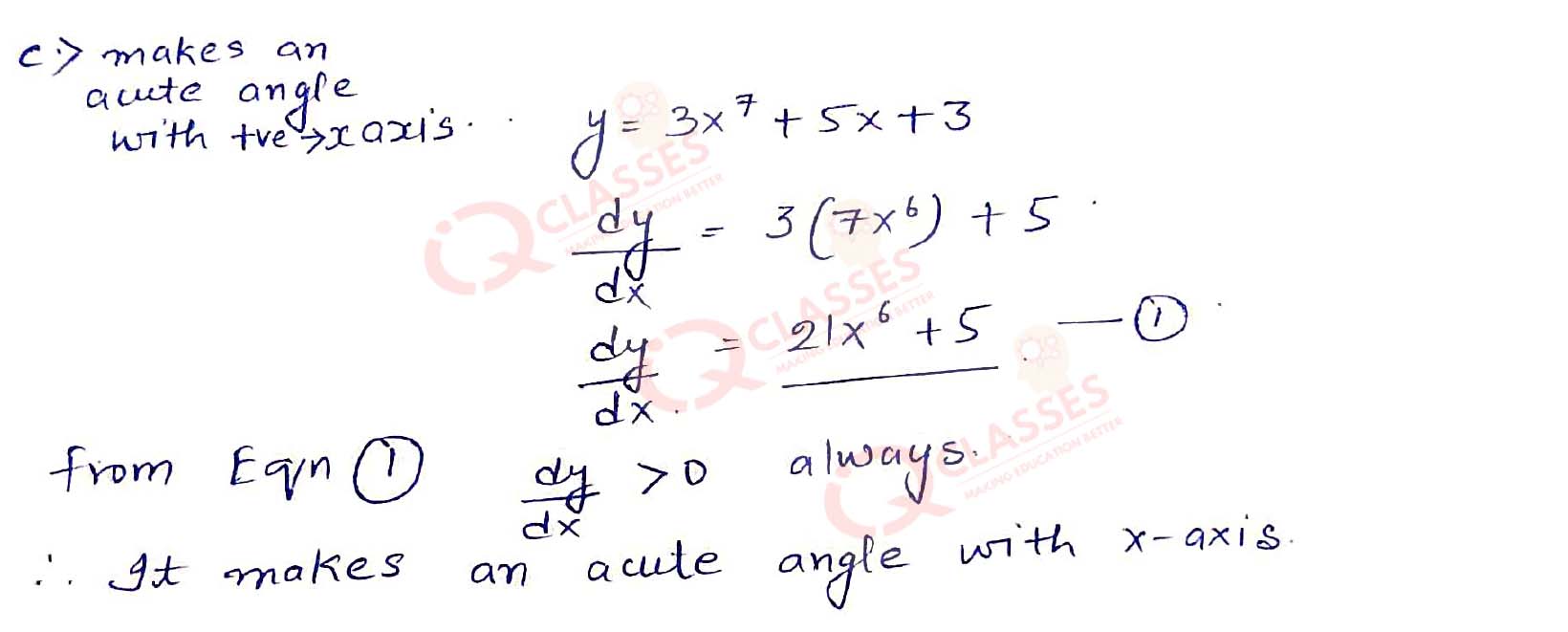
(20) What will be the derivative of sin^-1 with respect to cos^-1

1. -1
2. 1
3. 2
4. 4

Solution

(21) Ramu purchased 5 pens, 3 bags and 1 instrument box and paid ` 16. From the same shop Venkat purchased 2 pens , 1 bag and 3 instrument boxes and paid ` 19 while Gopi purchased 1 pen, 2 bags and 4 instrument boxes and paid ` 25.
Using the concept of Matrices and Determinants to answer the following questions by choosing the correct option:

1. If 𝑥, 𝑦 & 𝑧 respectively denotes the cost of pen, bag and instrument box then which of the following is true?
   1. 5𝑥 + 3𝑦 + 𝑧 = 16
   2. 2𝑥 + 𝑦 + 3𝑧 = 19
   3. 𝑥 + 2𝑦 + 4𝑧 = 25
   4. All of the above
2. If 𝐴 = , |𝐴|is:
   1. -22
   2. 22
   3. 22
   4. 0
3. If 𝐴 = and 𝑎𝑑𝑗 𝐴= then missing value of 𝑥 and 𝑦 are:
   
   1. 𝑥 = −10 & 𝑦 = −1
   2. 𝑥 = 10 & 𝑦 = −1
   3. 𝑥 = −10 & 𝑦 = 1
   4. 𝑥 = 10 & 𝑦 = 1
4. The cost of one pen is
   1. 2
   2. 5
   3. 1
   4. 3

Solution

(22) A Norman window is constructed by adjoining a semicircle to the top of an ordinary rectangular window as shown in the figure given below. The total perimeter of the window is 10 m.

Based on the above information answer the following by choosing the correct option:

1. If the length and breadth of the rectangle portion of the window is y and x respectively (as shown in the figure above) then the relation between the variable is
   1. y =20 +(𝜋−2)𝑥/4
   2. y =20 -(𝜋+2)𝑥/2
   3. y =20 -(𝜋+4)𝑥/4
   4. y =20 -(𝜋+2)𝑥/4
2. Let A be the area of the Norman window which admits the sunlight. Then A expressed in terms of x is
   1. A = 5x + 𝜋/4 𝑥²− 2𝑥²
   2. A = 5x + 𝜋/8 𝑥²− 1/2 𝑥²
   3. A = 5x - 𝜋/8 𝑥²− 1/2 𝑥²
   4. A = 5x - 𝜋/2 𝑥²− 1/4 𝑥²
3. For the maximum value of A what will be the radius of the semicircle
   1. 10/2+𝜋
   2. 10/𝜋-2
   3. 10/4+𝜋
   4. 10/4-𝜋
4. For maximum value of A , the length of the rectangle represented by y will be equal to:
   1. 10/4+𝜋
   2. 10/𝜋-2
   3. 20/4+𝜋
   4. 20/4-𝜋

Solution

(23) Consider the mapping 𝑓: 𝐴 → 𝐵 is defined by 𝑓(𝑥) = 𝑥−1/𝑥−2 such that 𝑓(𝑥) is one-one onto. Based on the above information, answer the following questions by choosing the correct option.

1. Domain of 𝑓(𝑥) is:
   1. 𝑅 − {2}
   2. R
   3. 𝑅 − {1, 2}
   4. 𝑅 − {0}
2. Range of 𝑓(𝑥) is:
   1. 𝑅 − {2}
   2. R
   3. 𝑅 − {1}
   4. 𝑅 − {0}
3. If 𝑔(𝑥) = 2𝑓(𝑥) − 1, then 𝑔(𝑥) in terms of 𝑥 is:
   1. 𝑥+2/x
   2. x+1/x-2
   3. x-2/x
   4. x/x-2
4. A function 𝑓(𝑥)is said to be one-one if
   1. 𝑓(𝑥1) = 𝑓(𝑥2) ⟹ 𝑥1 = 𝑥2
   2. 𝑓(𝑥1) = 𝑓(𝑥2) ⟹ 𝑥1 = 𝑥2
   3. 𝑓(𝑥1) = 𝑓(𝑥2) ⟹ −𝑥1 = 𝑥2
   4. −𝑓(𝑥1) = 𝑓(𝑥2) ⟹ 𝑥1 = 𝑥2

Solution

(24) What will be the value of m if the vector 2𝑖̂+ 𝑚𝑗̂+ 𝑘̂ is perpendicular to 2𝑖̂− 𝑗̂+ 3𝑘̂?

1. 7
2. 0
3. 1
4. -1

Solution

(25) What will be the angle between the two lines

1. 𝜋/2
2. 𝜋/4
3. 0
4. 𝜋

Solution

(26) What are the direction ratios of the line passing through two points (-2, 4, 5) and (1, 2, 3)?

1. < 1, 2, 3>
2. < −3, 2, 2>
3. < 2, 4, 5>
4. < 0, −1, 4>

Solution

(27) The equation of the line passing (1, −1, 0) and parallel to the line is:

Solution

(28) The given figure shows an air plant holder which is in the shape of a tetrahedron. Let A(1, 1, 1), B(2, 1, 3), C(3, 2, 2) & D(3, 3, 4) are the vertices of air plant holder. Based on the above information answer the following questions.

1. The vector of AB⃗    is:
   1. −𝑖̂− 2𝑘̂
   2. 2𝑖̂+ 𝑘̂
   3. 𝑖̂+ 2𝑘̂
   4. −2𝑖̂− 𝑘̂
2. The vector of AB⃗    is:
   1. 2𝑖̂− 𝑗̂− 𝑘̂
   2. 2𝑖̂+ 𝑗̂+ 𝑘̂
   3. −2𝑖̂− 𝑗̂+ 𝑘̂
   4. ̂𝑖̂+ 2𝑗̂+ 𝑘̂
3. Area of ∆𝐴𝐵𝐶 is:
   1. √11/2 Sq. units
   2. √14/2 Sq. units
   3. √13/2 Sq. units
   4. √17/2 Sq. units
4. The unit vector along the AB⃗    is:
   1. −2𝑖̂−𝑘̂/√5
   2. −𝑖̂−2𝑘̂/√5
   3. 2𝑖̂+𝑘̂/√5
   4. 𝑖̂+2𝑘̂/√5

Solution

(29) A company sells its product for ₹ 20 per unit. Fixed costs for the company is ₹ 45,000 and variable costs is estimated to run 25% of total revenue. If 𝑥 denotes number of units produced, then what will be the total cost function?

1. 45000 + 5x
2. 15000 + 4x
3. 45000 + 2x
4. 4500 + 20x

Solution

(30) The demand function for a certain commodity is given by 𝑝 = 4000 − 100𝑥 . What will be the total revenue from the sale of 3 units?

1. 11,100
2. 1000
3. 4500
4. 2000

Solution

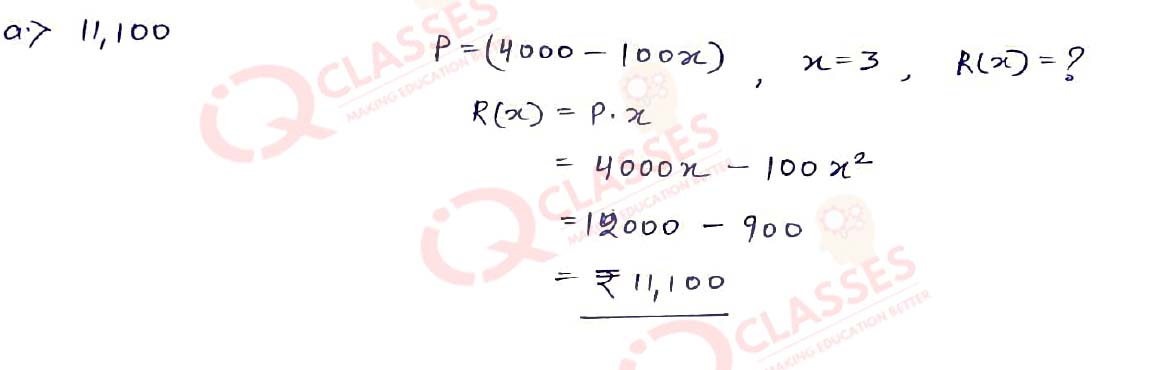
(31) A company sells 𝑥 packets of biscuits each day at ₹ 10 a packet. The cost of manufacturing these packets is ₹ 5 per packet plus a fixed daily overhead cost of ₹ 700. What will be the profit function?

1. 6𝑥 – 400
2. 5𝑥 – 700
3. 10𝑥 – 500
4. 5𝑥 – 10

Solution

(32) The cost function of a firm is given by (𝑥) = 3𝑥 2 − 2𝑥 + 6. The average cost of the firm at 𝑥 = 3 is

1. 11
2. 17
3. 9
4. 27

Solution

(33) The demand function for a certain product is represented by the equation: 𝑝 = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 where 𝑥 is the number of units demanded and 𝑝 is the price per unit.

1. The revenue function 𝑅(𝑥) is:
   1. 𝑎𝑥³ + 𝑏𝑥² + 𝑐x
   2. 𝑎𝑥 + 𝑏 +𝑐/x
   3. 𝑎𝑥³+ 𝑏𝑥² + 𝑐𝑥 + d
   4. 2𝑎𝑥 + b
2. The marginal revenue 𝑀𝑅(𝑥) is
   1. 𝑎 −𝑐/𝑥²
   2. 3𝑎𝑥² + 2𝑏𝑥 + c
   3. 3𝑎𝑥³ + 2𝑏𝑥² +c
   4. 2a
3. The slope of the marginal revenue is
   1. 0
   2. 6𝑎𝑥 + 2𝑏
   3. 2𝑐/𝑥³
   4. 9𝑎𝑥² + 4bx
4. Values of 𝑥, for which marginal revenue increases is:
   1. 𝑥 >−𝑏/3a
   2. 𝑥 <−𝑏 /3a
   3. 𝑥 =−𝑏/3a
   4. 𝑥 ≤ −𝑏/3a

Solution