Q25 Find the particular solutions of the following differential equations :
- y' - y = ex, given that y = 1 when x = 0
- y' + y = ex, given that y = 1/2 when x = 0
- xy' + y = x log x, given that y =1/4 when x=1
- xy' - y = log x, given that y = 0 when x = 1
- (1 + x2) dy /
dx +2xy =
1 / 1+x2 ,
given that y=0 when x = 1
- dy /
dx + 2y tan x = sin x, given that y = 0 when x = π/3
- y' + 2y = e-2x sin x, given that y = 0 when x =0
- xy' + y = x cos x + sin x, given that y = 1 when x = π/2
dy /
dx
+2xy =
1 / 1+x2
,
given that y=0 when x = 1 dy /
dx
+ 2y tan x = sin x, given that y = 0 when x = π/3 Solution
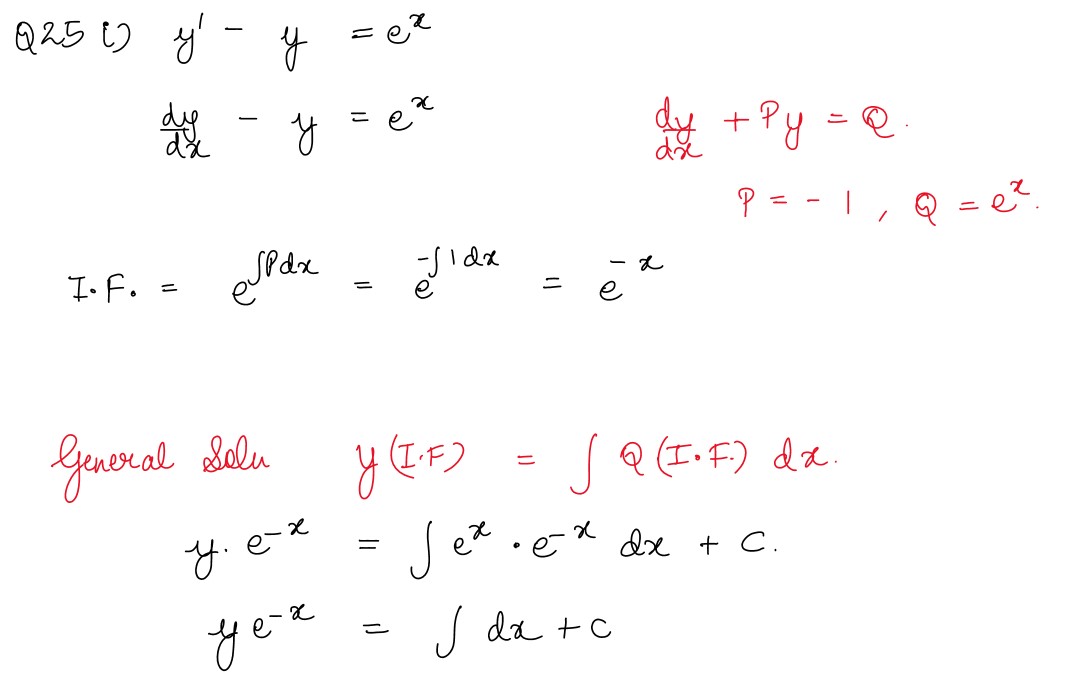 ,
,
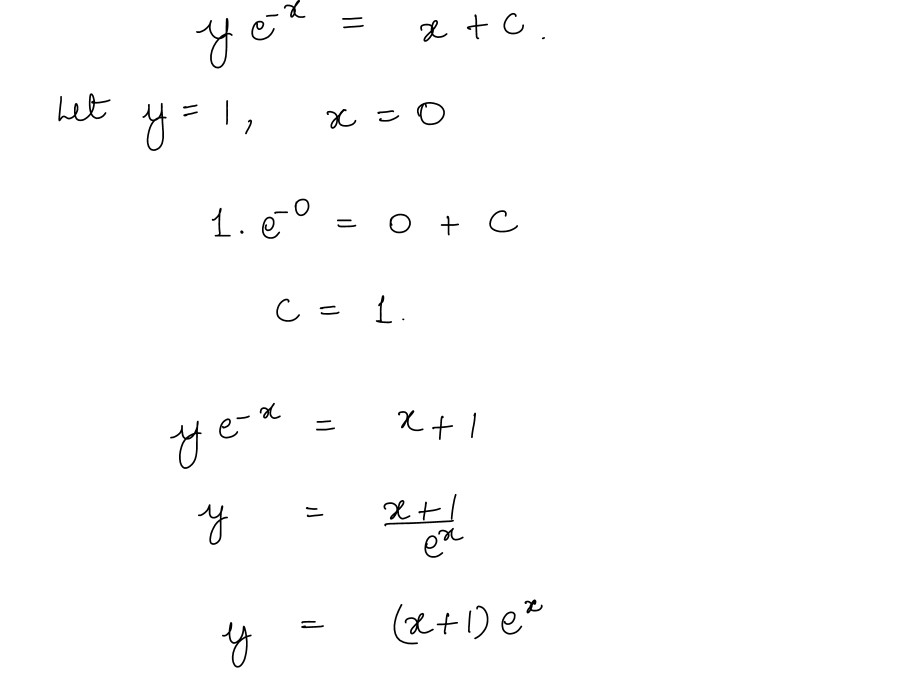 ,
,
.jpg) ,
,
-1.jpg) ,
,
.jpg) ,
,
-1.jpg) ,
,
-2.jpg) ,
,
.jpg) ,
,
-1.jpg) ,
,
-2.jpg) ,
,
-3.jpg) ,
,
.jpg) ,
,
-1.jpg) ,
,
-2.jpg) ,
,
.jpg) ,
,
-2.jpg) ,
,
.jpg) ,
,
-1.jpg) ,
,
.jpg) ,
,
-1.jpg)