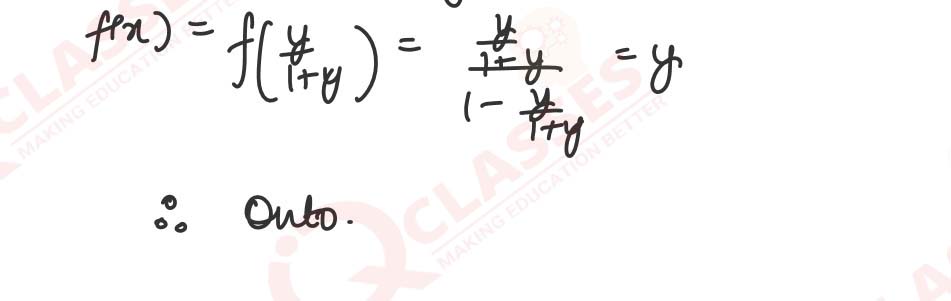Let N be the set of all natural numbers and R be a relation on N x N defined by

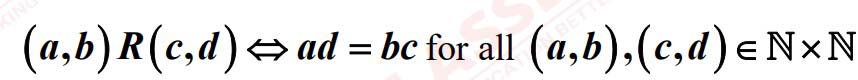.Show that R is an equivalence relation on N xN. Also, find the equivalence class of (2,6),i.e., [(2,6)]

OR

Show that the function f: R->{x ∈ R: -1 < x< 1} defined by f(x)=x/1+|x|,x ∈ R is one-one and onto function.

Solution

,,,,,,,,,
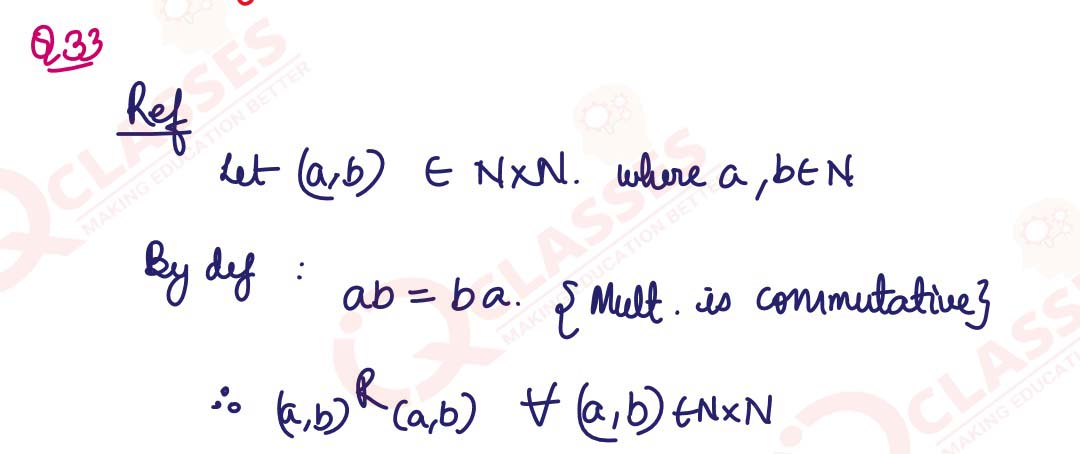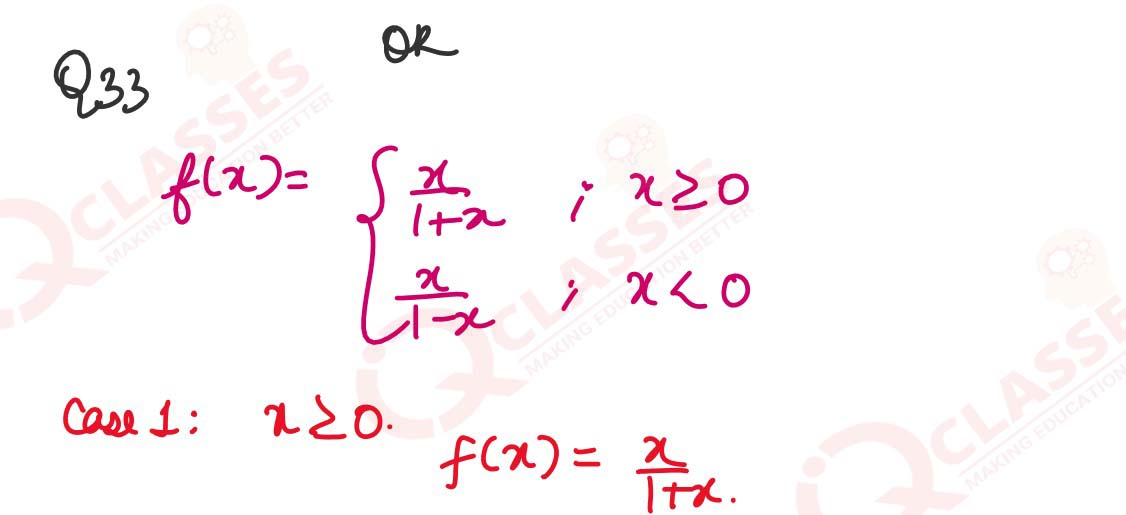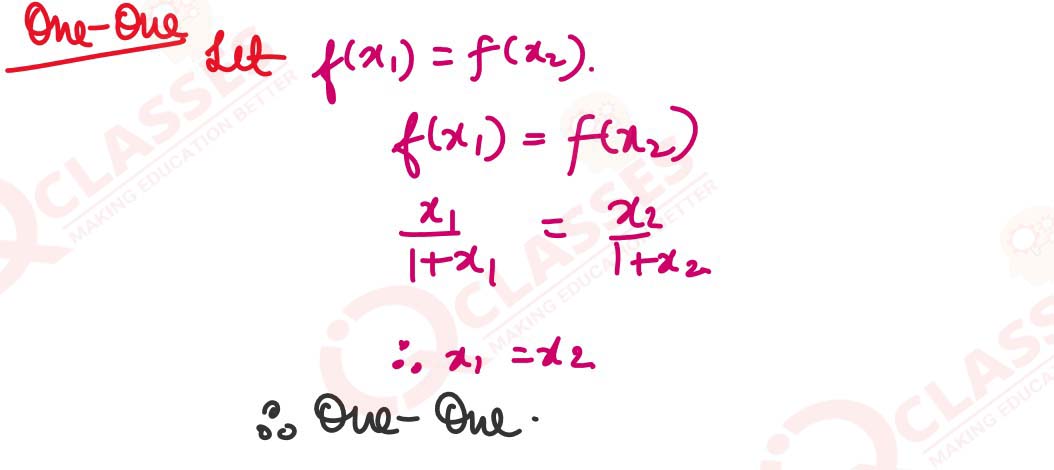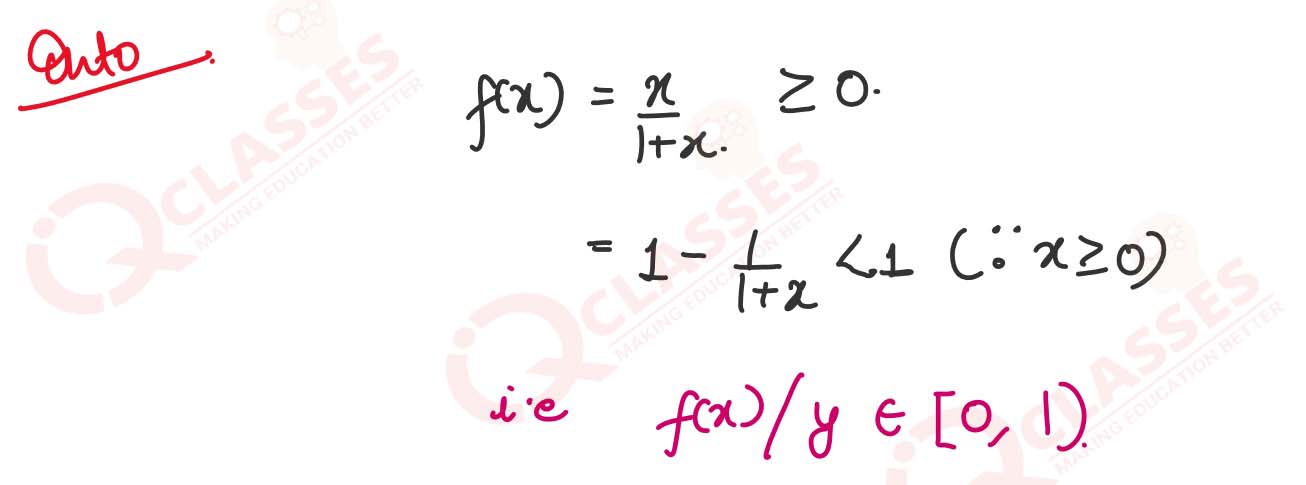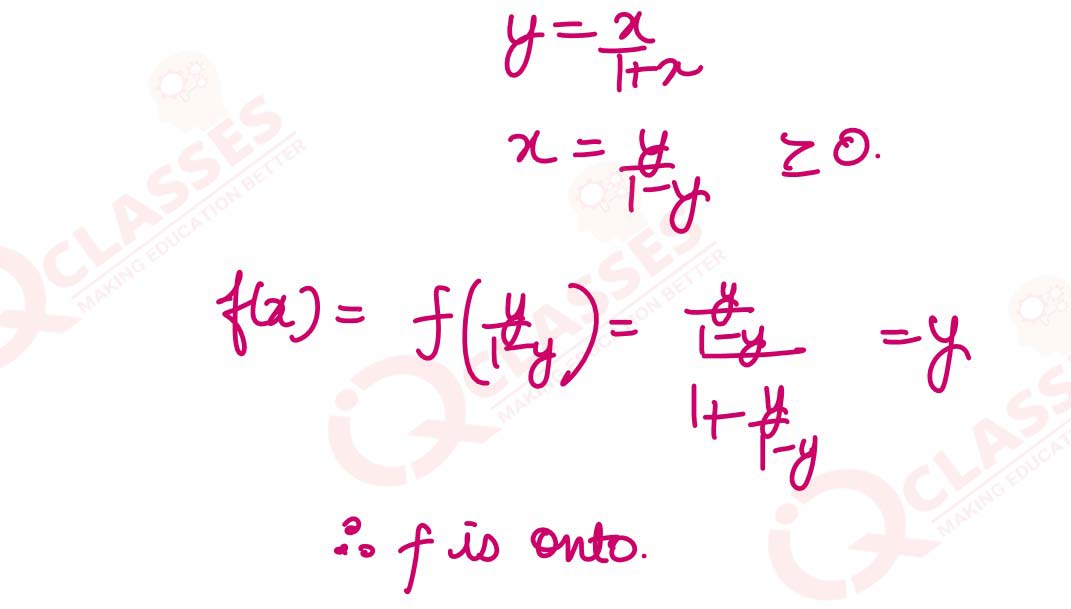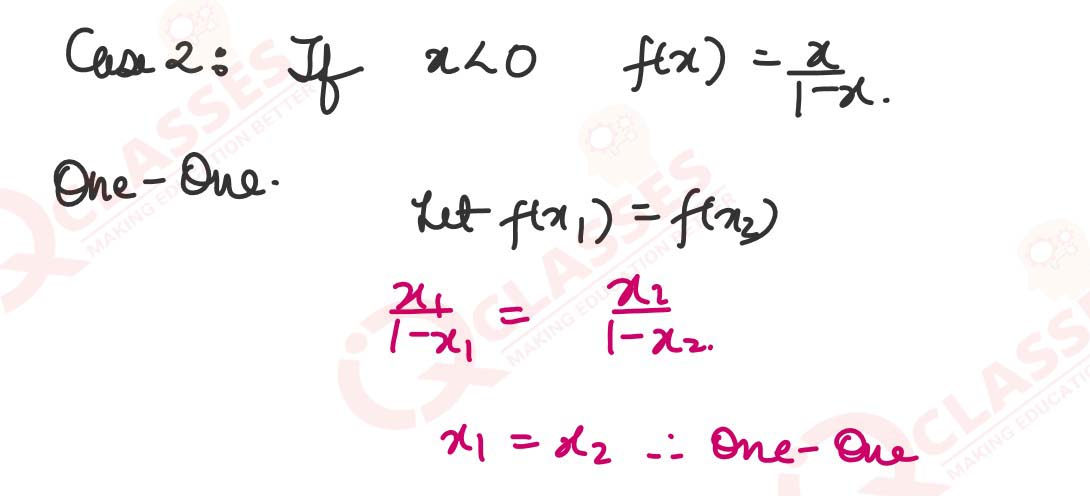