Let f(x) be a polynomial function of degree 6 such that


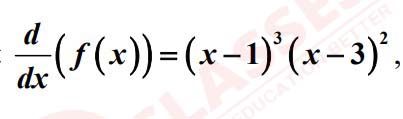
ASSERTION (A): f (xdy) has a minimum at x = 1.

REASON (R): When 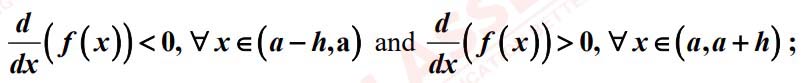where 'h' is an infinitesimally small positive quantity, then f (x) has a minimum at x=a, provided f(x) is continuous at x=a .

Solution

,,
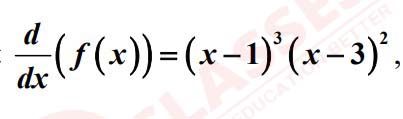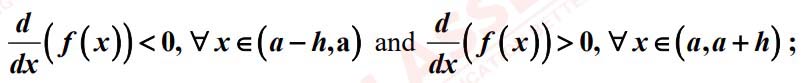