Q28 Without expanding any of the determinants given below, prove that
a2 b2 c2 (a+1)2 (b+1)2 (c+1)2 (a-1)2 (b-1)2 (c-1)2
=4 a2 b2 c2 a b c 1 1 1
Solution
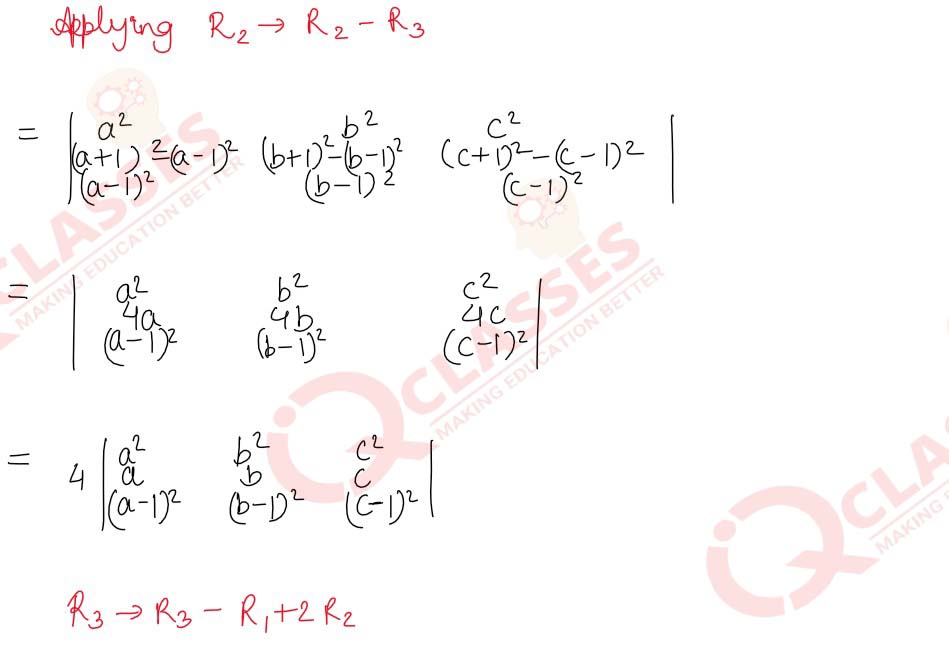 ,
,
| a2 | b2 | c2 |
| (a+1)2 | (b+1)2 | (c+1)2 |
| (a-1)2 | (b-1)2 | (c-1)2 |
| a2 | b2 | c2 |
| a | b | c |
| 1 | 1 | 1 |