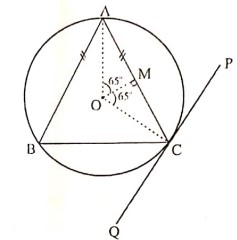
(i) In the given diagram, an isosceles ▵ABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.
Find:
(a) ∠ABC
(b) ∠BAC
(c) ∠BCQ


(ii) Solve the following inequation, write down the solution set and represent it on the real number line.


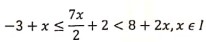
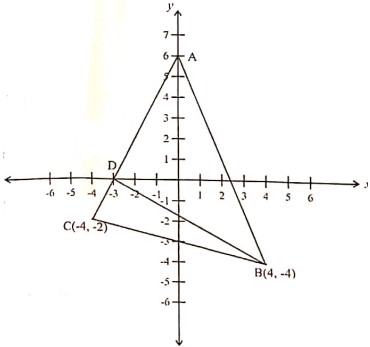
(iii) In the given diagram, ABC is a triangle, where B(4,-4) and C(-4, -2). D is a point on AC.
(a) Write down the coordinates of A and D.
(b) Find the coordinates of the centroid of ▵ABC.
(c) If D divides AC in the ratio k: 1, find the value of
(d) Find the equation of the line BD.

Solution

,,
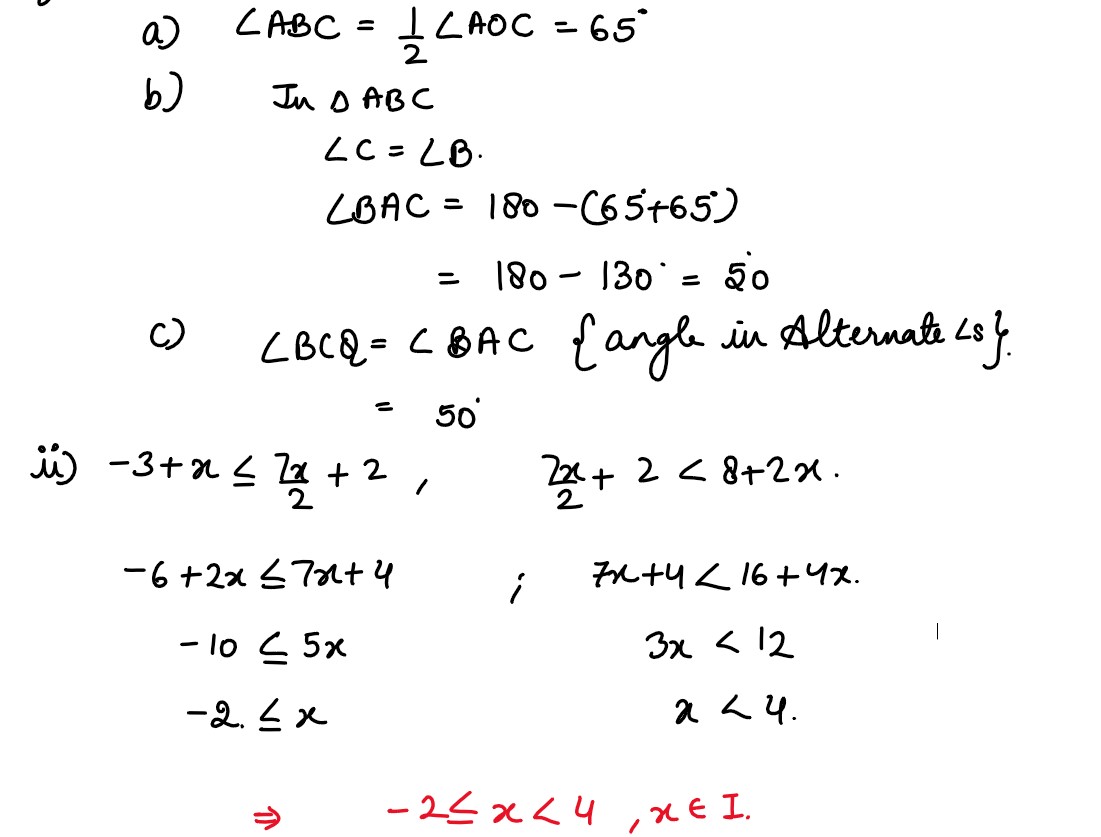