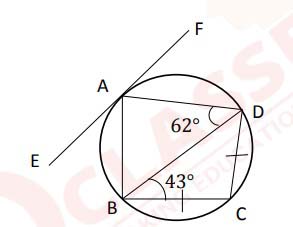
(i) Solve the following inequation write the solution set and represent it on the real number line



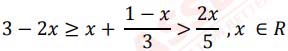
(ii) ABCD is a cyclic quadrilateral in which BC = CD and EF is a tangent at A. ∠CBD = 43° and ∠ADB = 62°. Find:
(a) ∠ADC
(b) ∠ABD
(c) ∠FAD


(iii) A (a, b), B(-4, 3) and C(8,-6)are the vertices of a ∆ABC. Point D is on BC such that BD : DC is 2 : 1 and M (6, 0) is mid point of AD. Find:
(a) coordinates of point D.
(b) coordinates of point A.
(c) equation of a line passing through M and parallel to line BC.

Solution

,,