Class 12 Maths ISC Vectors Board Questions
Here we provide Class 12 maths important notes,board questions and predicted questions with Answers for chapter Vectors. These important notes,board questions and predicted questions are based on ISC board curriculum and correspond to the most recent Class 12 maths syllabus. By practising these Class 12 materials, students will be able to quickly review all of the ideas covered in the chapter and prepare for the Class 12 Board examinations.
2016
Q1
(a) For any 3 vectors a⃗ , b⃗, c⃗, show that a⃗ - b⃗, b⃗ -
c⃗, c⃗ - a⃗ are co-planer
(b) Find the unit vector perpendicular to each of the vector a⃗ + b⃗ and a⃗ - b⃗ where a⃗ = 3 î + 2ĵ + 2k^ and b⃗ = î + 2 ĵ 2k^
solutions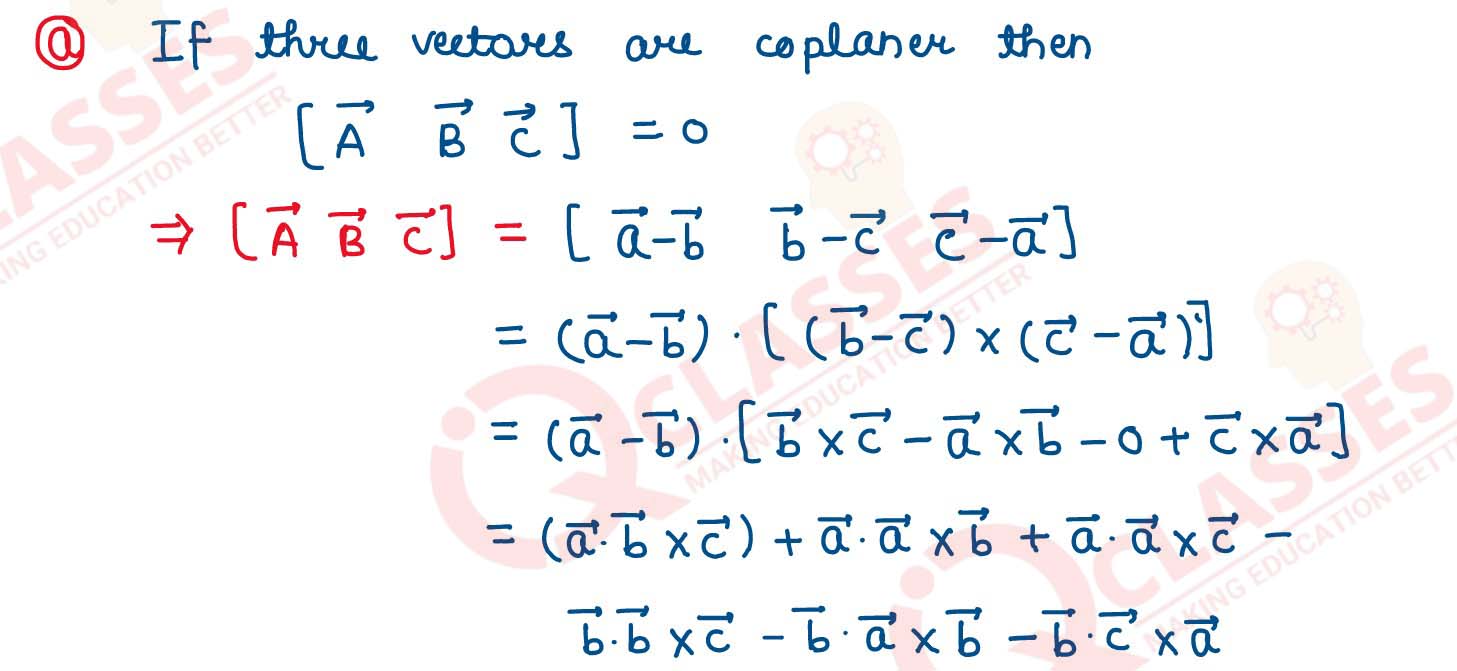




(b) Find the unit vector perpendicular to each of the vector a⃗ + b⃗ and a⃗ - b⃗ where a⃗ = 3 î + 2ĵ + 2k^ and b⃗ = î + 2 ĵ 2k^
solutions
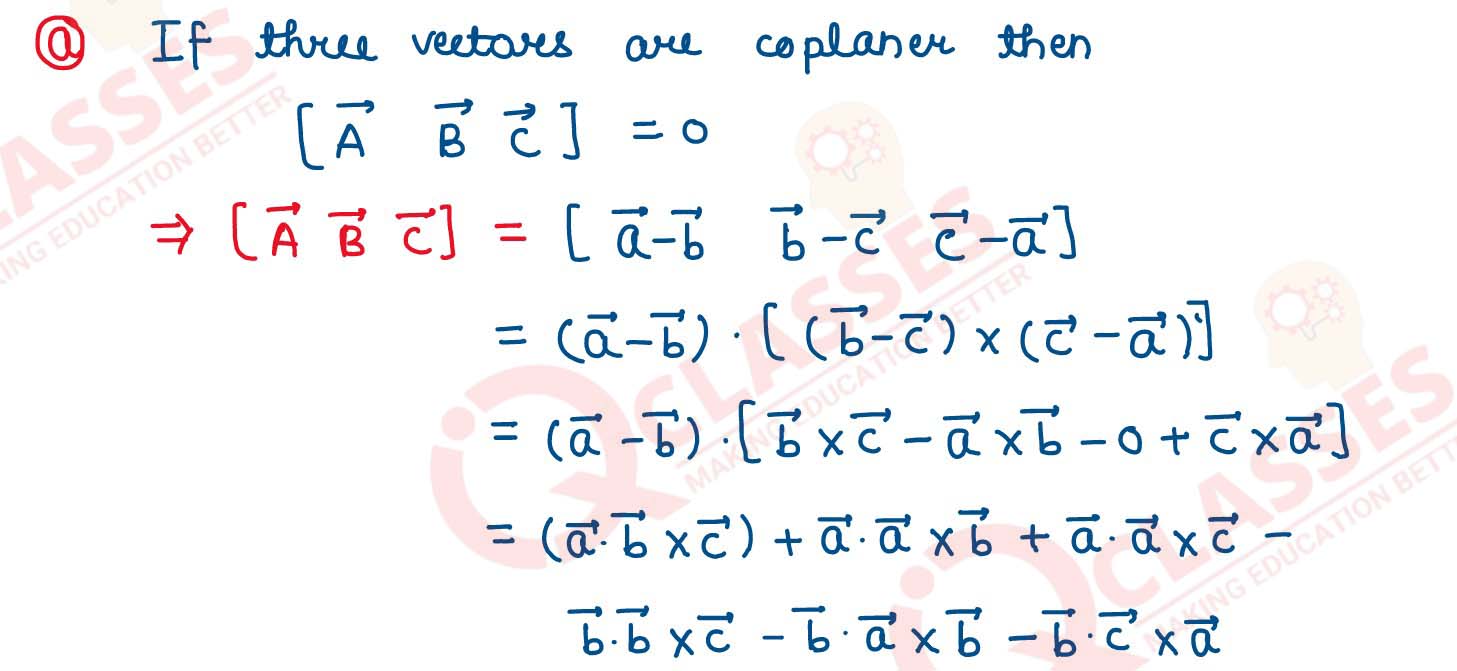




2017
Q2
(a) If a⃗, b⃗ and c⃗ are 3 mutually perpendicular vectors of equal magnitude ,prove
that (a⃗ + b⃗ + c⃗) is equally inclined with vectors a⃗, b⃗ and
c⃗
(b) Find the value of λ for which the following 4 point with position vectors 6î - 7ĵ , 16î - 19î -4k^ , λĵ - 6k^ and 2î - 5ĵ + 10k^ are coplaner
solutions




(b) Find the value of λ for which the following 4 point with position vectors 6î - 7ĵ , 16î - 19î -4k^ , λĵ - 6k^ and 2î - 5ĵ + 10k^ are coplaner
solutions





2018
Q3
(a) If A,B,C are 3 non collinear points with position vectors a⃗, b⃗ and c⃗
respectively, then show that the length of the perpendicular from C on AB is
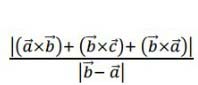
OR
(b) Show that the 4 points A,B,C and D with position vectors 4î + 5ĵ + k^, -ĵ -k^, 3î + 9ĵ + 4k^ and 4(î + ĵ + k^) respectively are co-planer
solutions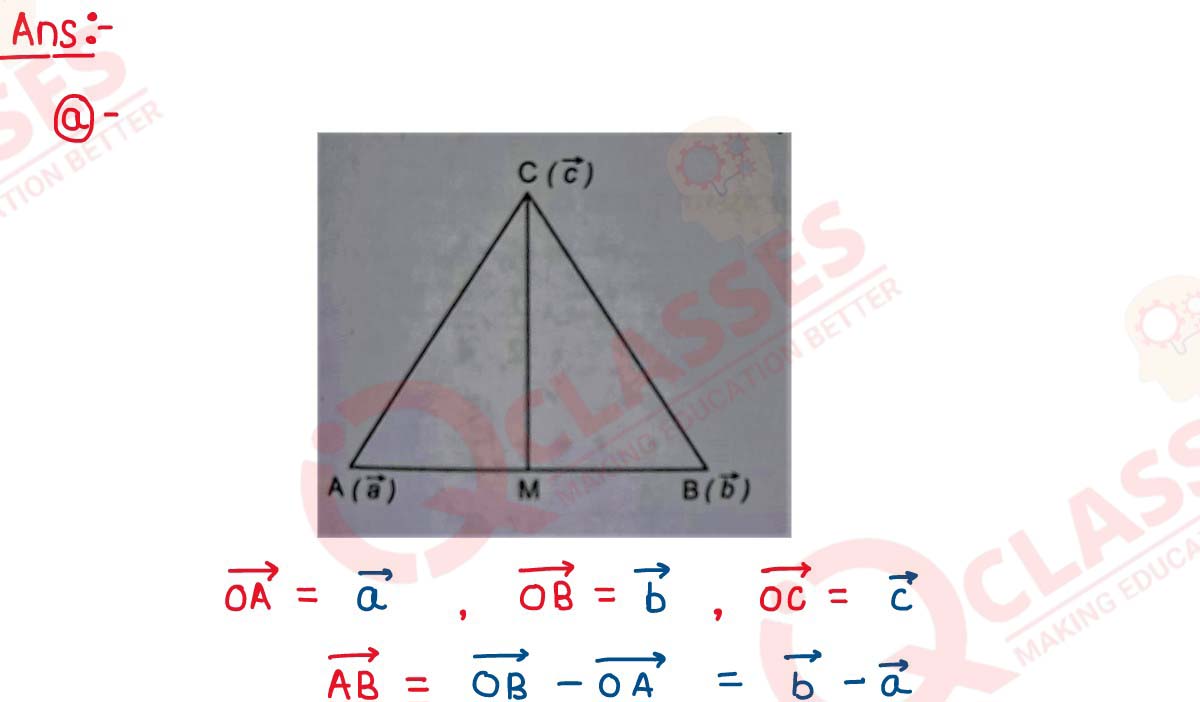



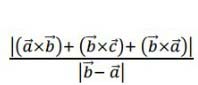
(b) Show that the 4 points A,B,C and D with position vectors 4î + 5ĵ + k^, -ĵ -k^, 3î + 9ĵ + 4k^ and 4(î + ĵ + k^) respectively are co-planer
solutions




Q4
Find the image of the point having position vector : 3î - 2ĵ + k^ in the plane r⃗.(3î - ĵ +
4k^) = 2
solutions

solutions


2019
Q5
(a) If a⃗ = i -2j +3k , b⃗ = 2i + 3j - 5k, prove that a⃗ and a⃗ x b⃗
are perpendicular.
OR
(b) If a⃗ and b⃗ are non-collinear vectors , find the value of x such that the vector α⃗ = (x - 2)a⃗ + b⃗ and β = (3 + 2x)a⃗ - 2b⃗ are collinear.
solutions
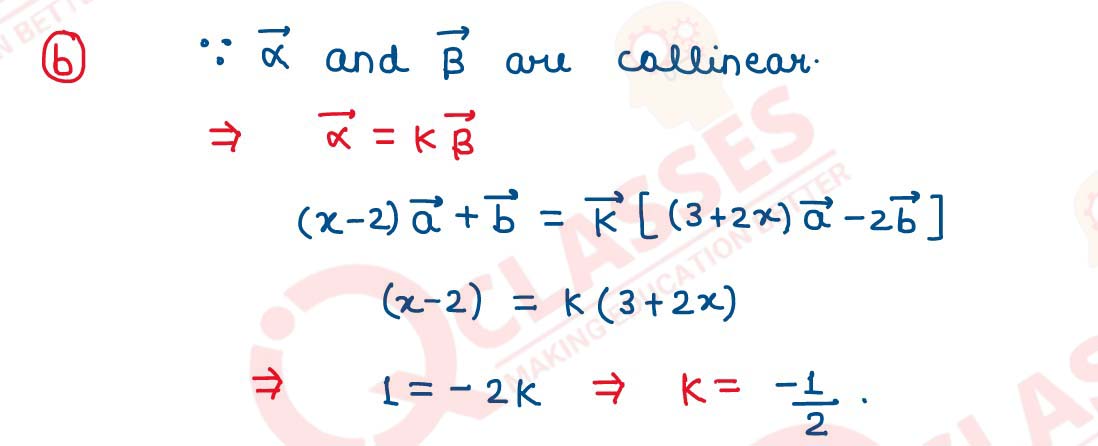

(b) If a⃗ and b⃗ are non-collinear vectors , find the value of x such that the vector α⃗ = (x - 2)a⃗ + b⃗ and β = (3 + 2x)a⃗ - 2b⃗ are collinear.
solutions

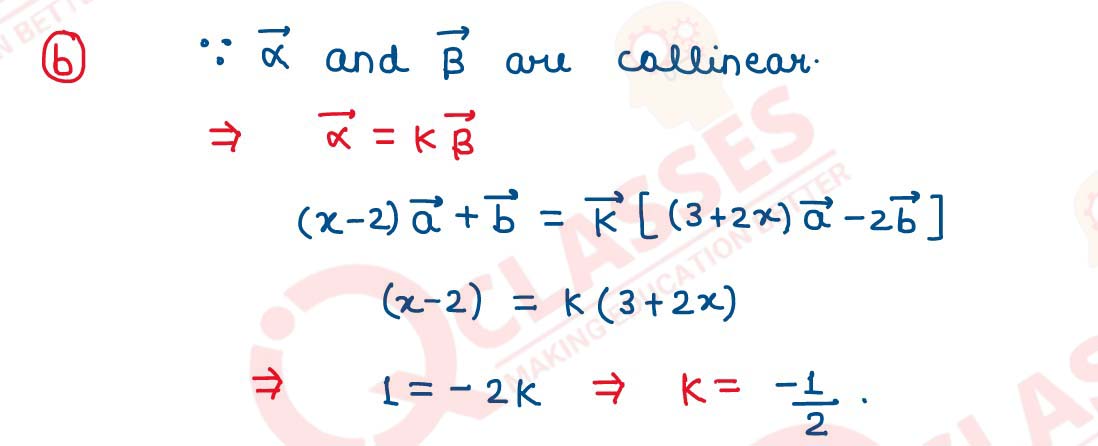

Q6
(a) If a⃗ abd b⃗ are perpendicular vectors |a⃗ + b⃗| = 13 and |a⃗| = 5
, find the value of |b⃗|
(b) Find the length of the perpendicular from origin to the plane r⃗.(3i - 4j -12k)+ 39 = 0
solutions

(b) Find the length of the perpendicular from origin to the plane r⃗.(3i - 4j -12k)+ 39 = 0
solutions


2020
Q7
Write a vector of magnitude of 18 unit in the direction of the vector î - 2ĵ - 2k^
solutions
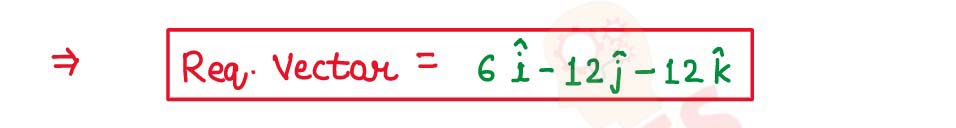
solutions

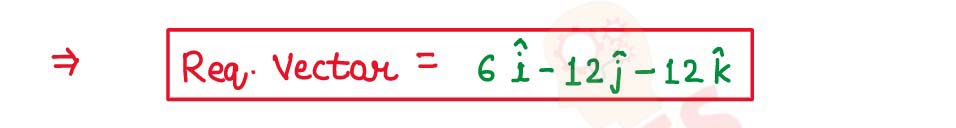
Q8
(a) Prove that aa⃗[(ba⃗ +ca⃗) x (aa⃗ + 3ba⃗ + 4ca⃗)] =
[aa⃗ ba⃗ ca⃗]
OR
(b) Using vectors find the area of the triangle whose vertices are : A(3,-1,2), B(1,-1,-3) and C(4,-3,1)
solutions



(b) Using vectors find the area of the triangle whose vertices are : A(3,-1,2), B(1,-1,-3) and C(4,-3,1)
solutions





Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment