Class XII ISC Chapter Continuity and Differentiability
Explore our extensive collection of Continuity and Differentiability questions, tailored for class 12 students following the ISC curriculum. This topic is vital for understanding how to optimize a particular outcome given certain constraints. Our practice questions cover various aspects of Linear Programming, including formulating linear inequalities, graphical methods, and finding optimal solutions. Whether you're looking to strengthen your problem-solving skills or prepare for your exams, these questions provide the perfect resource to master Continuity and Differentiability concepts with ease.
class 12 C&D exercise5-4
Continuity & Differentiability
Select Exercise
Q1 If a function is derivable at a point, is it necessary that it must be continuous at that point?
Solution

Q2 If a function is continuous at a point, is it necessary that it must be derivable at that point?
Solution
No,it is not necessary that the function is derivable at that point where it is continous
Q3 Is the function f(x) = |x| derivable at x = 0?
Solution

Q4 Is the function f(x) = cot x derivable at x = 0?
Solution

Q5 Is the function f(x) = sec x derivable at x = π/2
Solution

Q6 When a function is called derivable?
Solution
A function is derivable at a point where there is a defined derivative at that point. This means that the slope of the tangent line of the points from the left is approaching the same value as the slope of the tangent of the points from the right.
Q7
Which of the following functions are derivable?
- sin x
Solution
.jpg)
-1.jpg)
Solution
.jpg)
-1.jpg)
Q8
Examine the function
f(x)=
1+x ,if x≤2
5-x ,if x>2
for differentiability at x=2
| 1+x ,if x≤2 |
| 5-x ,if x>2 |
Solution


Q9
Examine the following function for continuity at x = 1 and differentiability at x = 2.
f(x)=
5x-4 ,0< x< 1
4x2-3x ,1< x< 2
3x+4 ,x≥2
| 5x-4 ,0< x< 1 |
| 4x2-3x ,1< x< 2 |
| 3x+4 ,x≥2 |
Solution


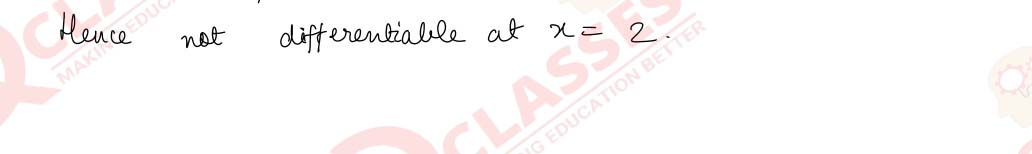
Q10 Show that the function f(x) = 2x — |x| is continuous at x = 0 but not differentiable at x=0.
Solution
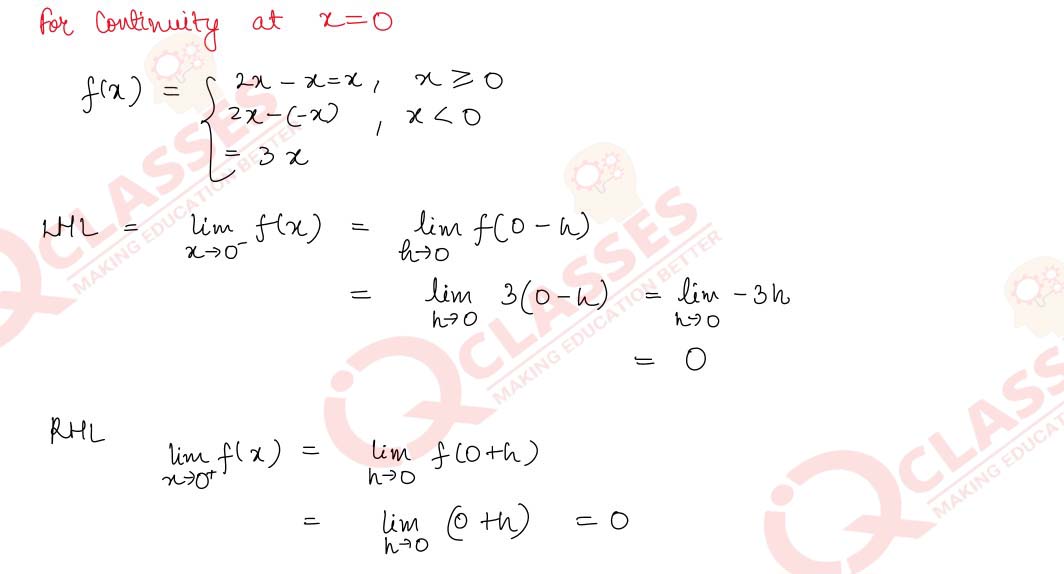


Q11 Show that f(x) = |x -5| is continuous but not differentiable at x = 5.
Solution



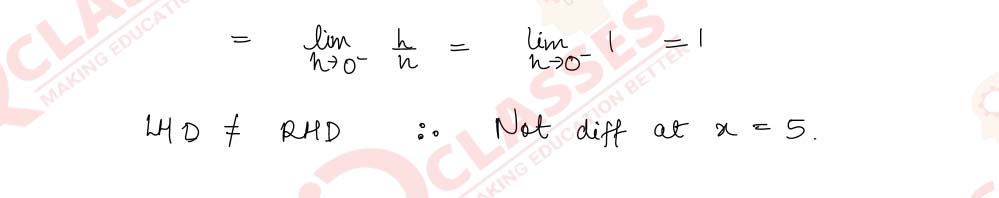
Q12 If the function f(x) = |x-3| + |x-4|, then show that f is not differentiable at x = 3 and x = 4.
Solution



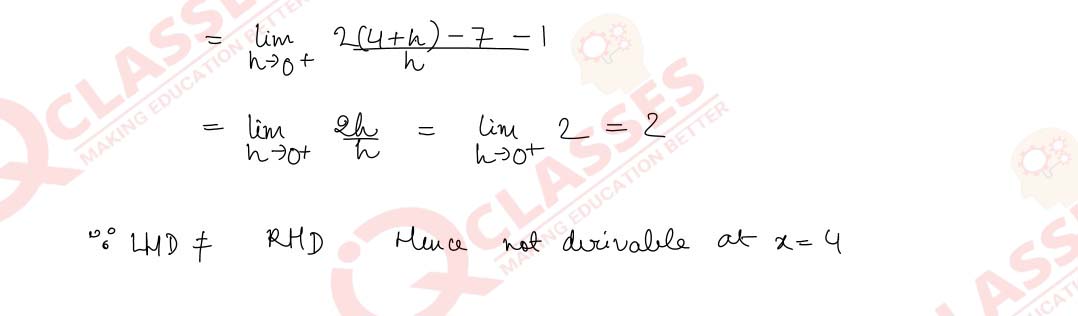
Q13
Show that the function f is continuous at x = 1 for all values of a where
f(x)=
ax2+1,x≥1
x+a ,x< 1
Find its right and left hand derivatives at x = 1. Hence, find the condition for the existence of
the derivative at x = 1.
| ax2+1,x≥1 |
| x+a ,x< 1 |
Solution




Q14
Prove that the function f(x)=
x
/
|x|
,x≠0
1, x=0
,is not differentiable at x=0
|
x
/
|x|
,x≠0
|
| 1, x=0 |
Solution


