Class XII ISC Chapter Probability Exercise 10.3
Access a comprehensive collection of probability questions, specially designed to help you grasp and apply this important mathematical topic. Our question bank covers various types of Integration, including first-order, second-order, homogeneous, and non-homogeneous equations, along with real-world applications in physics, engineering, and other fields. These practice questions will help you reinforce your problem-solving skills, deepen your conceptual understanding, and prepare effectively for exams. Whether you're a student or a learner aiming to master probability, our collection offers the perfect resource for practice and success.
class 12 Probability exercise2-1
Probability
Select Exercise
Q2 What is the probability of obtaining an even prime number on each die when a pair of dice is rolled?
Solution

Q3
(i) Events A and B are such that P(A) = 1/2 P(B) = 7/12 and P(not A or not B) = 1/4. State whether A and
B are independent.
(ii) Let E and F be events with P(E) = 3/5 P(F) = 3/10 and P(E ∩ F) = 1/5.
Are E and F independent?
Solution


Q4
(i) If P(A) = 3/5 and P(B) = 1/5 then find P(A ∩ B) if A and B are independent events.
(ii) If A and B are two independent events such that P(not B) = 0.65 and P(A U B) = 0.85, then find
P(A).
Solution

Q5 A fair coin and an unbiased die are tossed. Let A be the event 'head appears on the coin and B be the event '3 on the die'. Check whether A and B are independent events or not. .
Solution

Q6 A die is thrown. If E is the event 'the number appearing is a multiple of 3' and F be the event 'the number appearing is even', then find whether E and F are independent
Solution

Q7 A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event 'number is even' and B be the event 'number is red'. Are A and B independent?
Solution

Q8 If P(A) = 0.2, P(B) = p, P(A U B) = 0.6 and A and B are given to be independent events, find the value of p.
Solution

Q9
A coin is tossed thrice and all the eight outcomes are assumed to be equally likely. In which of the
cases are the events E1 and E2 independent? In which cases are mutually exclusive?
(i) E1 : the first throw results in head
E2 : the
last throw results in tail
(ii) E1 : the number of heads is two
E2 : the last throw results in head
(iii) E1 :
the number of heads is odd
E2 : the number of tails is odd.
Solution



Q10 An urn contains 10 black and 5 white balls. Two balls are drawn from the urn one aft another without replacement. What is the probability that both balls drawn
Solution

Q11 A bag contains 5 red, 6 white and 7 black balls. Two balls are drawn at random. what is the probability that both balls are red or both are black?
Solution

Q12 There are 2 red and 3 black balls in a bag. Three balls are taken out at random from the bag. Find the probability of getting 2 red and 1 black ball or 1 red and 2 black balls
Solution

Q13 A bag contains 5 white, 7 red and 4 black balls. Four balls are drawn one by one with replacement. What is the probability that none is white?
Solution

Q14 A bag contains 1 white, 5 red and 4 black balls. If three balls are drawn one by one without replacement, then find the probability of drawing a white ball followed by two red balls.
Solution
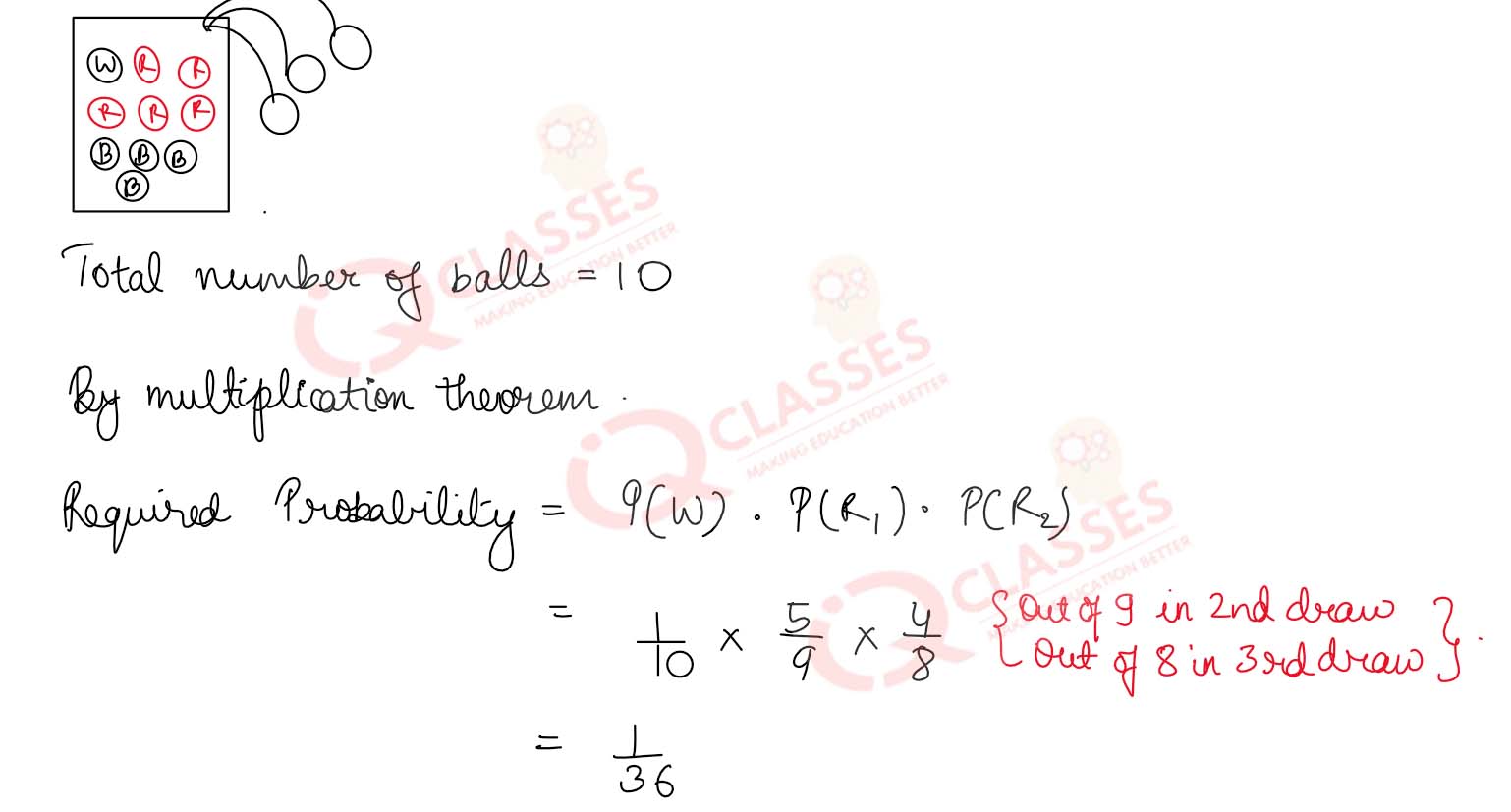
Q15
From a bag containing 20 tickets, numbered from 1 to 20, two tickets are drawn at random. Find the
probability that
(i) both the tickets have prime numbers on them
(ii) on one there is a prime number and on the other
there is a multiple of 4.
Solution

Q16
An urn contains 4 red and 7 blue balls. Two balls are drawn at random with replacement Find the
probability of getting
(i) 2 red balls
(ii) 2 blue balls
(iii) one red and one blue ball.
Solution

Q17 Three balls are drawn one by one without replacement from an urn containing 3 white, 3 red and 3 black balls. What is the probability that atleast one ball is red?
Solution

Q18 A box contains 100 tickets numbered 1 to 100. If 5 tickets are drawn successively with replacement from the box, find the probability that all the tickets bear numbers divisible by 10.
Solution

Q19 One bag contains 3 white balls, 7 red balls and 15 black balls. Another bag contains 10 white balls, 6 red balls and 9 black balls. One ball is taken from each bag. Find the probability that both balls will be of the same colour.
Solution

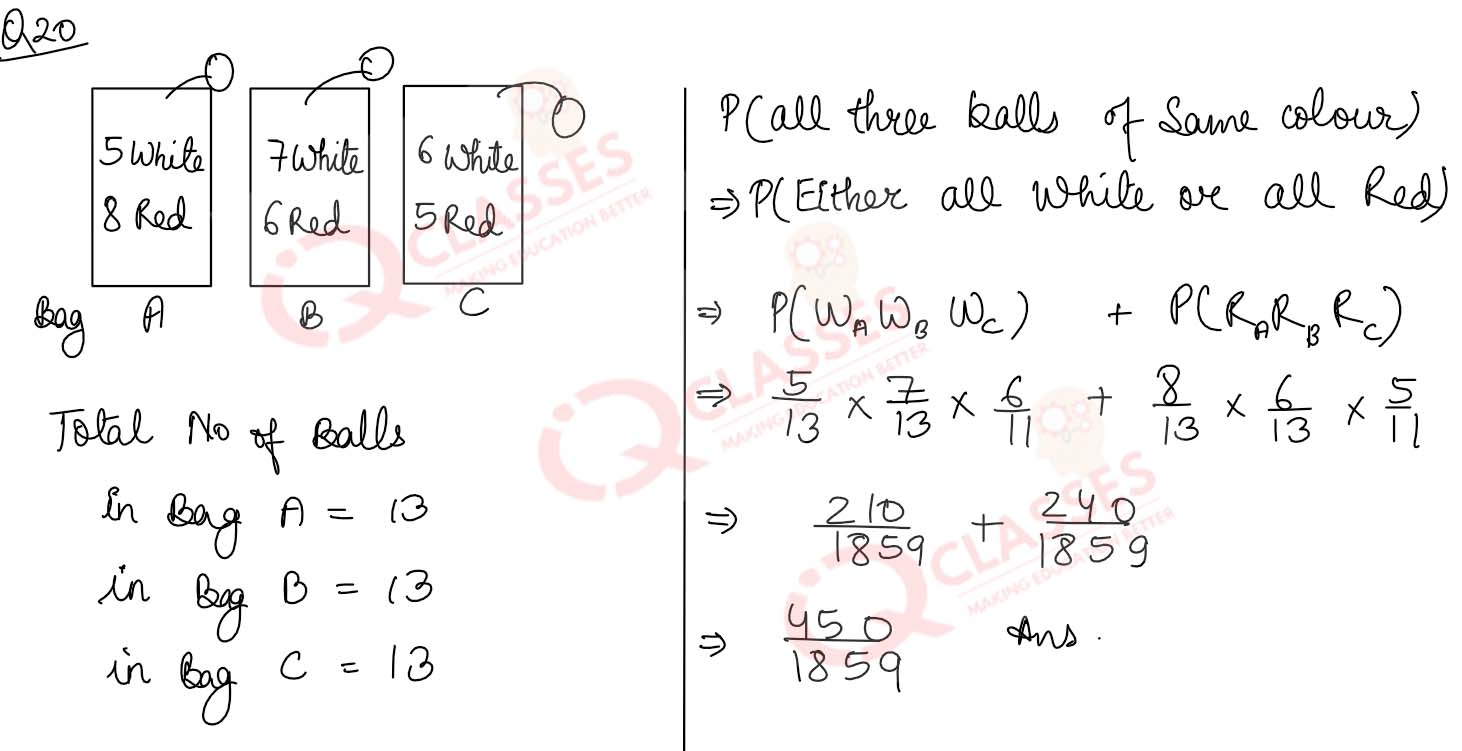
Q20 In bag A, there are 5 white and 8 red balls, in bag B, 7 white and 6 red balls, and in bag C, 6 white and 5 red balls. One ball is taken out at random from each bag. Find the that all the three balls are of the same colour.
Solution
Q21 In a group of students, there are 3 boys and 3 girls. Four students are to be selected at random from the group. Find the probability that either 3 boys and 1 girl, or 3 girls and 1 boy are selected.
Solution
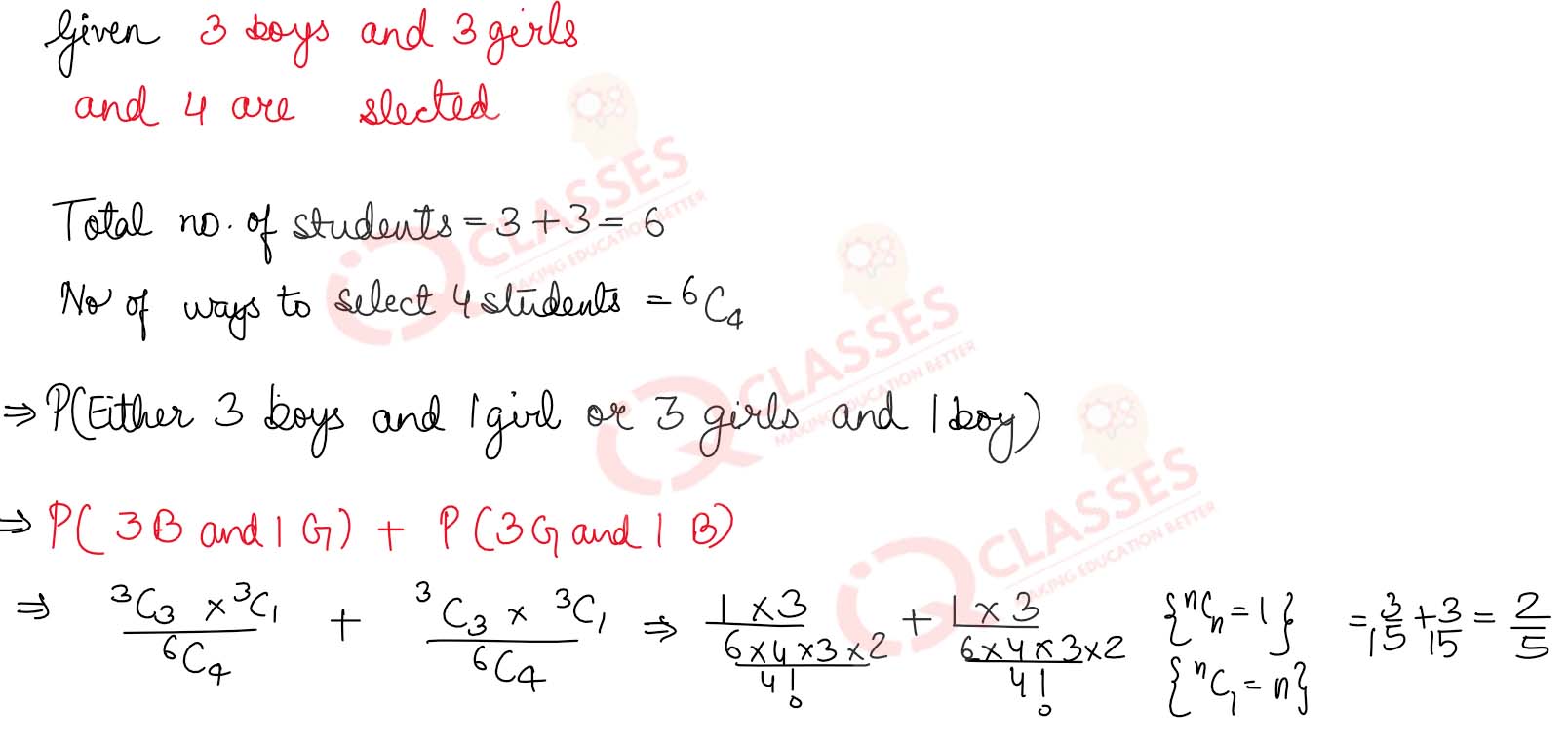
Q22
X is taking up subjects Mathematics, Physics and Chemistry in the examination. His probabilities of
getting grade A in these subjects are 0.2, 0.3 and 0.5 respectively. Find the probability that he
gets
(i) Grade A in all subjects
(ii) Grade A in no subject
(iii) Grade A in two subjects.
Solution

Q23
Three cards are drawn from a pack of well-shuffled 52 cards. Find the probability that
(i) all the
three cards are of the same suit
(ii) one is a king, the other is a queen and the third is a jack.
Solution

Q24 A bag contains 5 white and 4 black balls and another bag contains 7 white and 9 black balls. A ball is drawn from the first bag and two balls drawn from the second bag. What i5 the probability of drawing one white and two black balls?
Solution

Q25
Two dice are rolled once. Find the probability that
(i) the numbers on two dice are different
(ii) the total of numbers on the two dice is atleast 4.
Solution

Q26
In a single throw of three dice, find the probability of getting
(i) same number on the three
dice
(ii) a total of 5
(iii) a total of atmost 5
(iv) a total of atleast 5.
Solution

Q27
An urn contains 7 white, 5 black and 3 red balls. Two balls are drawn at random. Find the probability
that
(i) both the balls are red
(ii) one ball is red, the other is black
(iii) one ball is
white.
Solution

Q28 The probabilities of two students A and B coming to school in time are 3/7 and 5/7 respectively. Assuming that the events, 'A coming in time' and 'B coming in time' are independent, find the probability of only one of them coming to school in time. Write atleast one advantage of coming to school in time.
Solution

Q29
(i) Kamal and Monika appear for an interview for two vacancies. The probability of Kamal's selection is
1/3 and that of Monika's selection is 1/5 . Find the probability that only one of them will be
selected.
(ii) Akhil and Vijay appear for an interview for two vacancies. The probability of Akhil's selection is
1/4 and Vijay's selection is 2/3. Find the probability that only one of them 3 will be selected.
Solution


Q30
The probability of hitting a target at the first, second and third shots are
3
/
5
,
2
/
5
and
1
/
4
. Calculate the probability that the target gets hit.
Solution

Q31 The probability that a boy will not pass M.B.A. examination is 3/5 and that a girl will not pass is 4/5 . Calculate the probability that atleast one of them passes the examination. What ideal conditions a student should keep in mind while appearing in an examination?
Solution

Q32
A husband and a wife appear in an interview for two vacancies in the same post. The probability of
husband's selection is 1/7 and that of wife's selection is 1/5. What is the probability that
(i) both of them will be selected?
(ii) none of them will be selected?
(iii) only one of
them will be selected?
(iv) atleast one of them will be selected?
Solution

Q33 A machine operates if all of its three components function. The probability that the first component fails during the year is 0.14, the probability that the second component fails is 0.10 and the probability that the third component fails is 0.05. What is the probability that the machine will fail during the year?
Solution

Q34
A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cads are they likely
to contradict each other in stating the same fact?
Do you think that statement of B is true?
Solution

Q35
Ten Tickets are numbered 1 to 10. Two tickets are drawn one after other at random. Find the probability
that the number on one of the tickets is a multiple of 5 and other a multiple of 4 when the tickets are
drawn
(i) without replacement
(ii) with replacement.
Solution

Q36
A bag contains 5 red discs and 4 blue discs. If 3 discs are drawn from the bag without replacement, then
find the probability that
(i) all three are blue
(ii) there are 2 red and 1 blue
(iii)
the second disc is red.
Solution

Q37 A bag contains 5 white and 3 black balls. Four balls are successively drawn out without replacement. What is the probability that they are alternately of different colours? what would be the probability of this event if balls are drawn with replacement?
Solution

Q38
A bag contains one black and two white balls. A drawing from the bag consists of taking a ball from the
bag and keeping it out if it is white but putting it back if it is black Calculate the probabilities
that
(i) the first drawing is a white ball
(ii) the second drawing is a white ball
(iii) the
third drawing is a white ball. .
Solution

Q39
A bag contains 4 white and 2 black balls. Another contains 3 white and 5 black balls. If one ball is
drawn from each bag, then find the probability that
(i) both are white
(ii) both are black
(iii) one is white and one is black.
Solution

Q40 A bag contains 2 black, 4 white and 3 red balls. One ball is drawn at random and kept aside. Then another ball is drawn and kept aside. This process is continued till all the balls are drawn. Find the probability that the ball drawn are in the sequence 2 black. 4 white and 3 red.
Solution

Q41 A policeman fires four bullets on a dacoit. The probability that the dacoit will be killed by one bullet is 0.6. What is the probability that the dacoit is still alive?
Solution
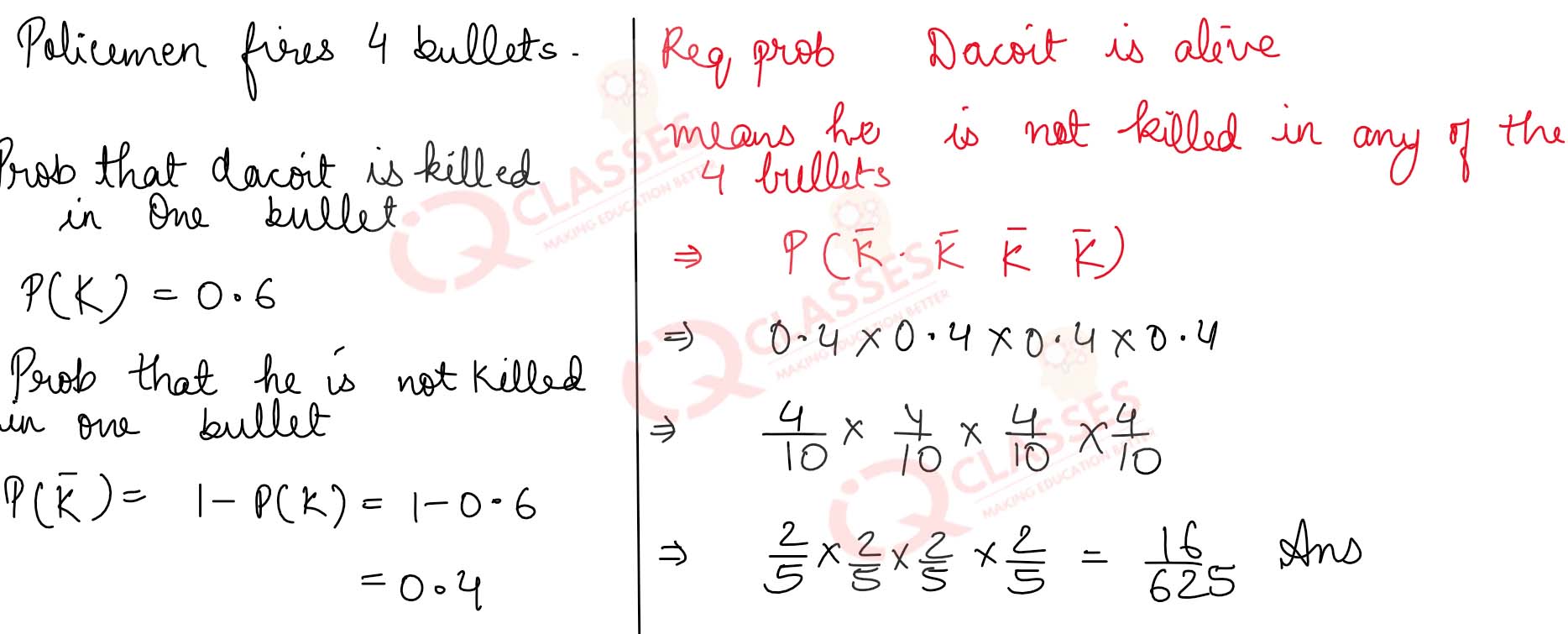
Q42 A and B toss a coin alternately till one of them gets a head and wins the game. If A starts first, then find the probability that B will win the game.
Solution

Q43 In a hockey match, both teams A and B scored same number of goals up to the end of the game, so to decide the winner, the referee asked both the captains to throw a die alternately and decided that the team, whose captain gets a six first, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match and state whether the decision of the referee was fair or not.
Solution

Q44 Aman and Bhuvan throw a pair of dice alternately. In order to win, they have to get a sum of 8. Find their respective probabilities of winning if Aman starts the game.
Solution

Q45 A and B cut a pack of 52 playing cards alternately and every time the card is put back. The pack is well-shuffled after each cut. A starts the game and the one who cuts a heart first wins. What are their respective probabilities winning?
Solution

Q46 A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B if he gets a total of 10. If A starts the game, find the probability that B wins the game.
Solution



Add a comment