1 What is an alternating current (AC)?

Show that the average value of AC over a complete cycle is zero while for a half-cycle it is 2I_o/π, where I_o is the peak value of the current. Solution

2 Show that I_rms=l_o/√2, where I_rms is the root- mean-square value of the alternating current and lo is its peak value. Solution

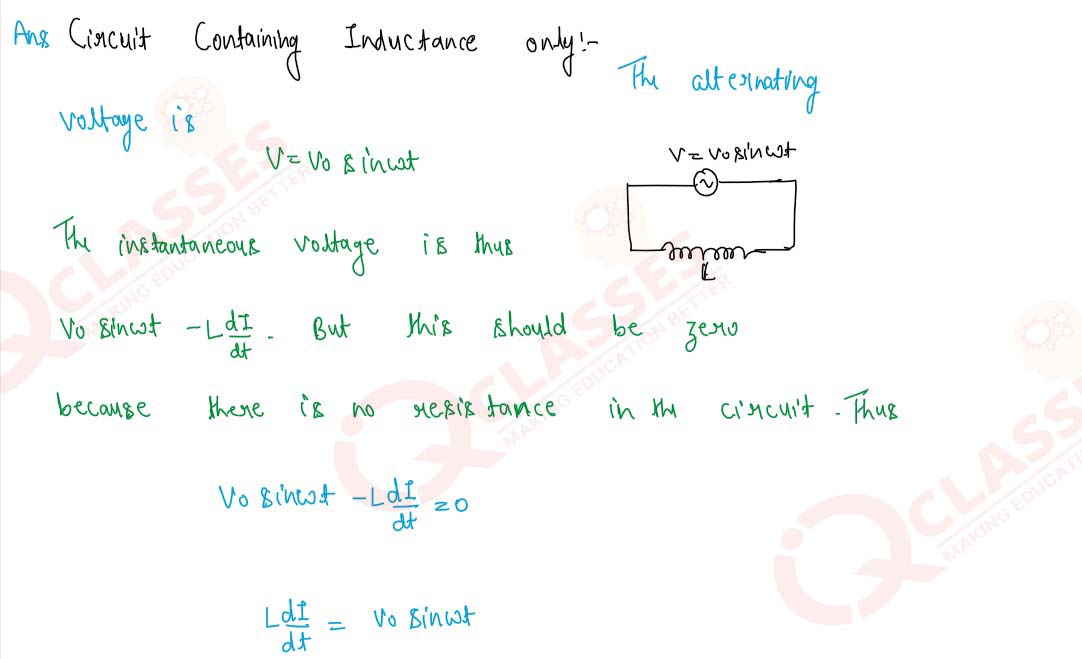
3 Show mathematically that in an AC circuit containing inductance only, the current lags behind the voltage by π/2 Solution

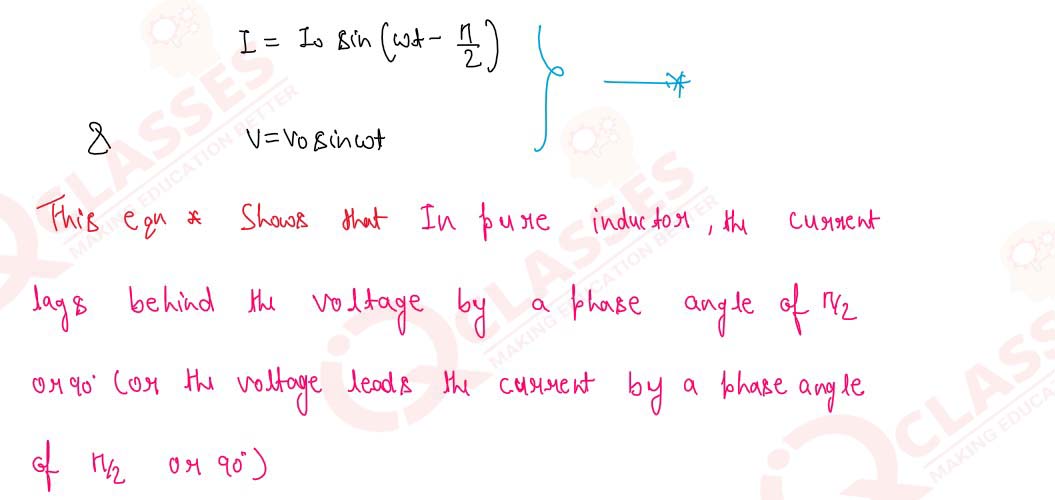
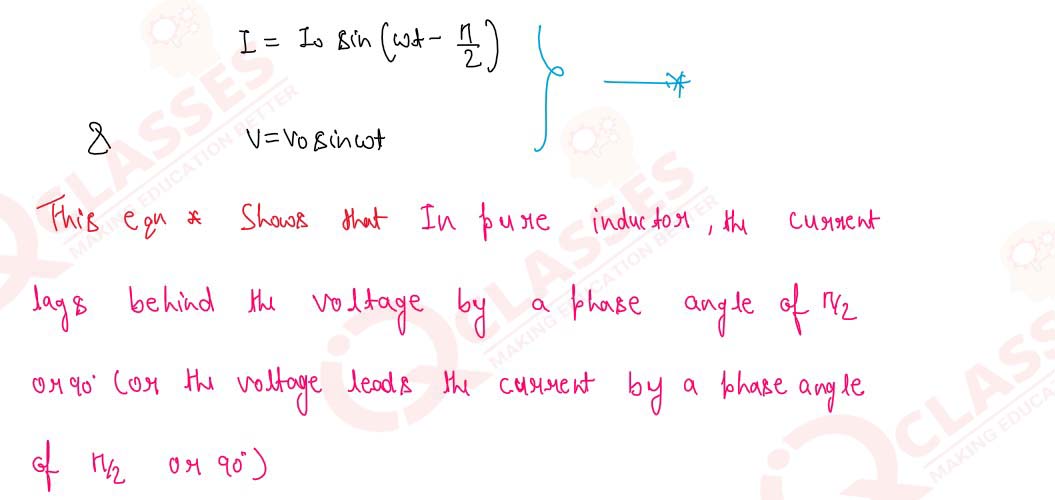
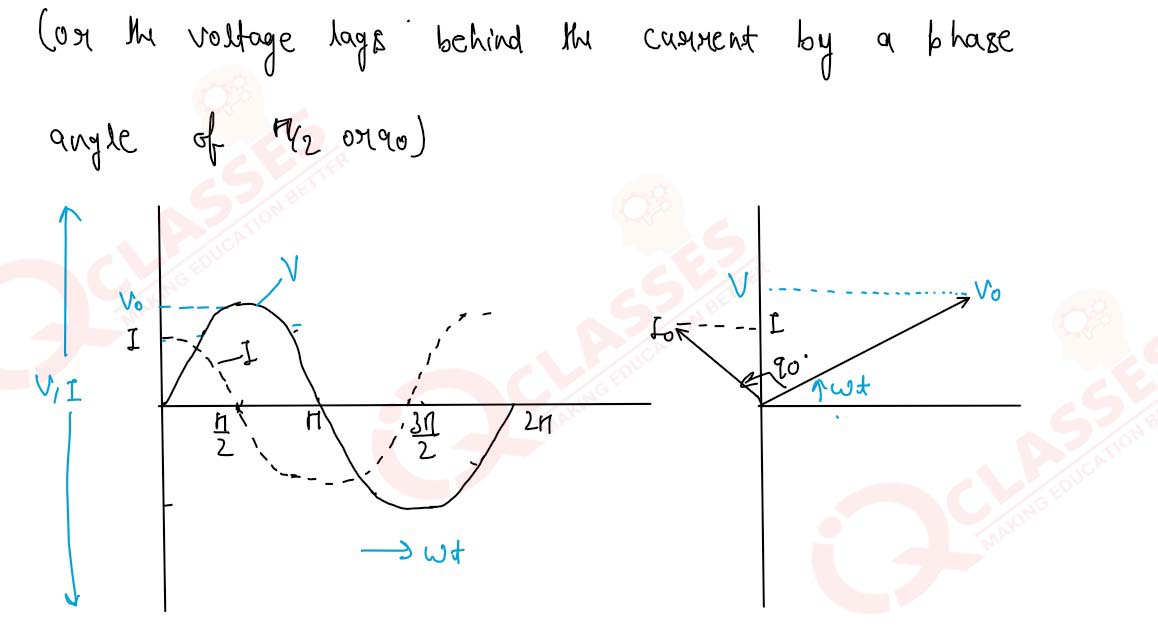
4 Show mathematically that in a pure capacitive AC circuit, the current leads the voltage by r/2. Solution

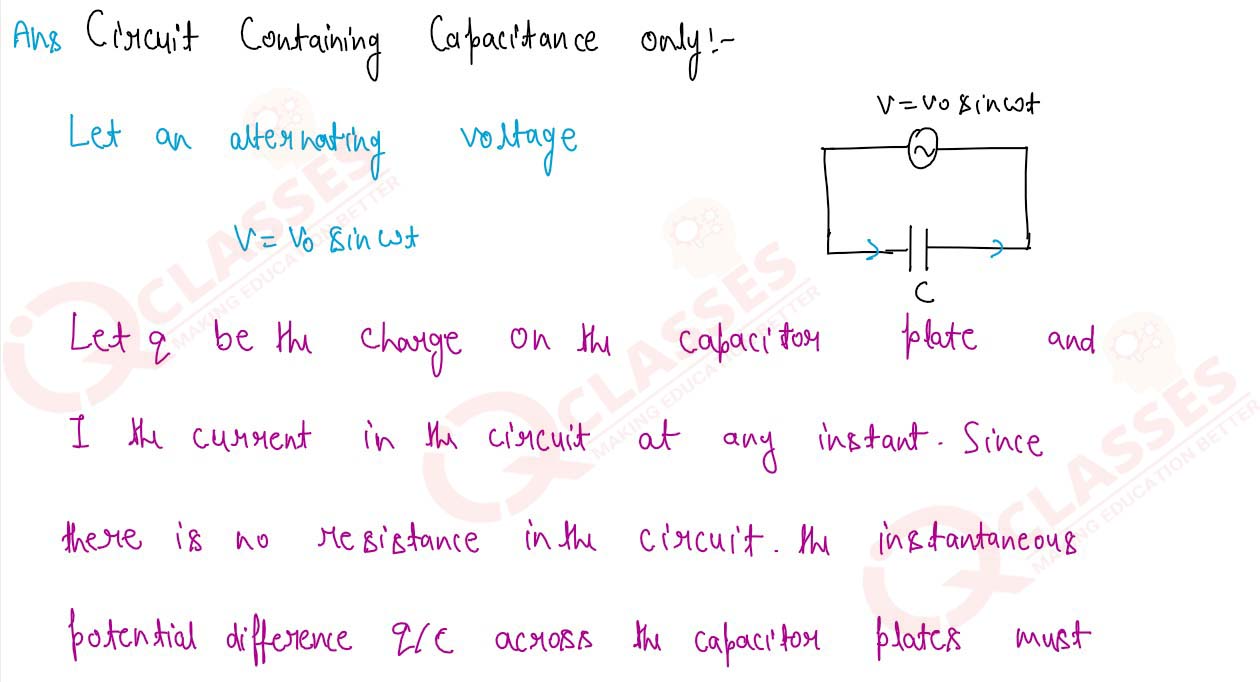
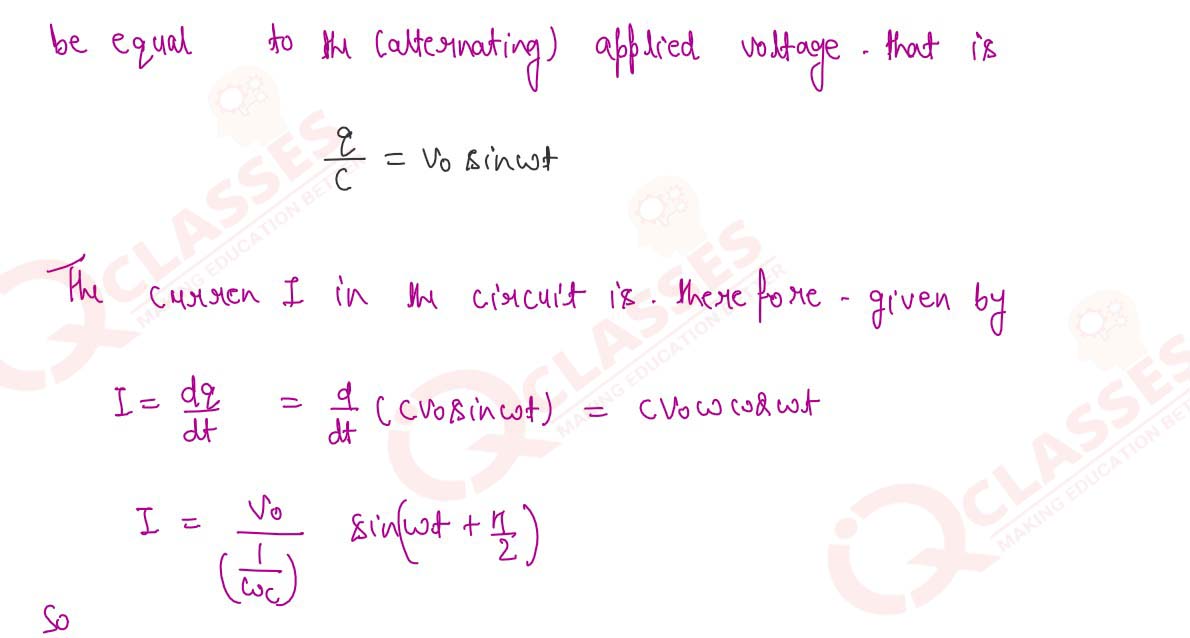
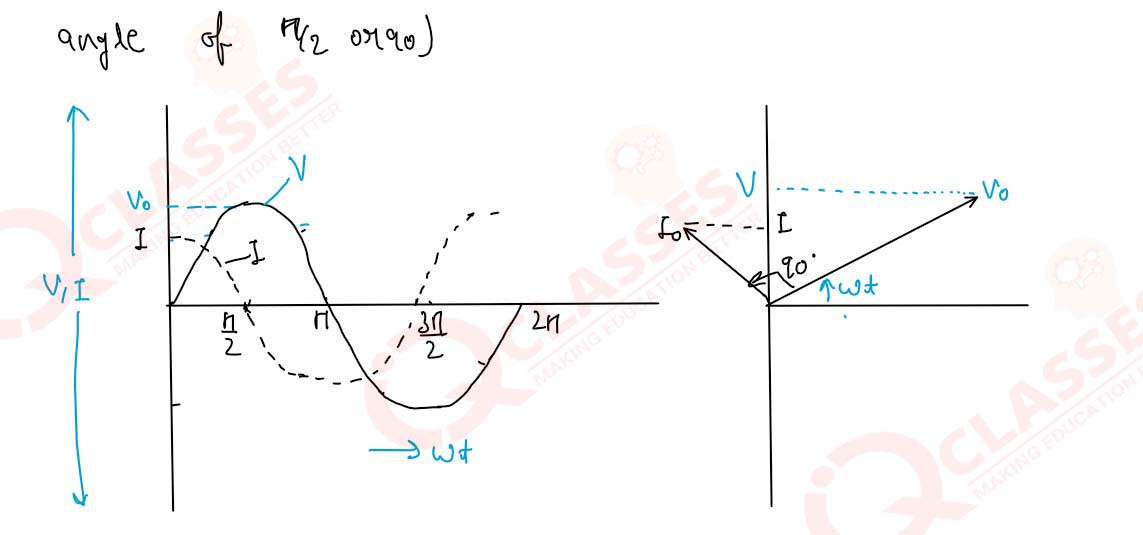
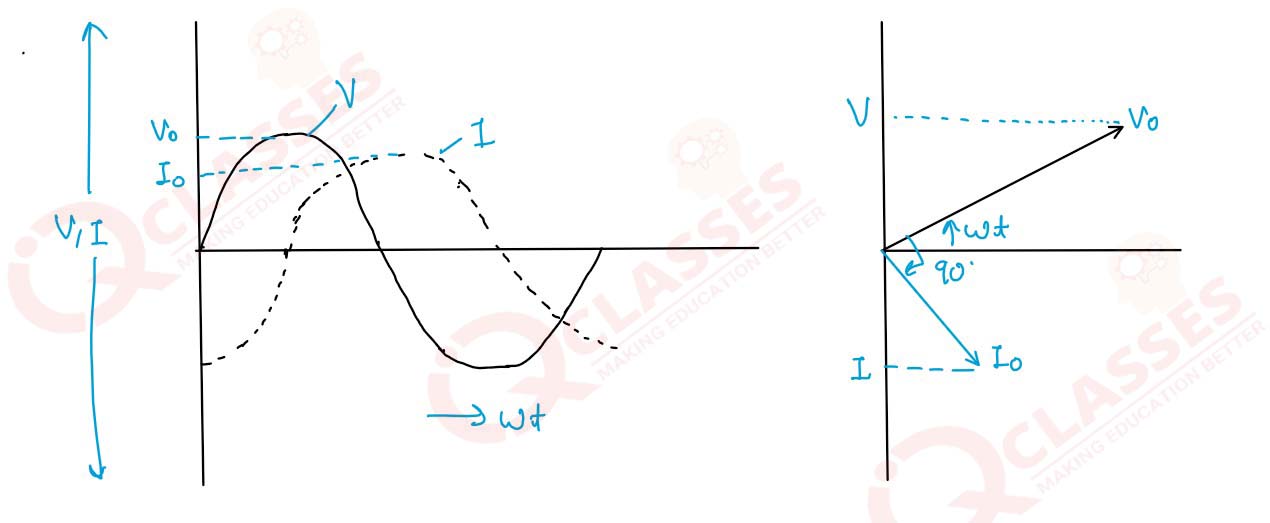
5 Show, with explanation, the variations of emf and current with time in AC circuits having pure resistance, pure inductance and pure capacitance. Solution

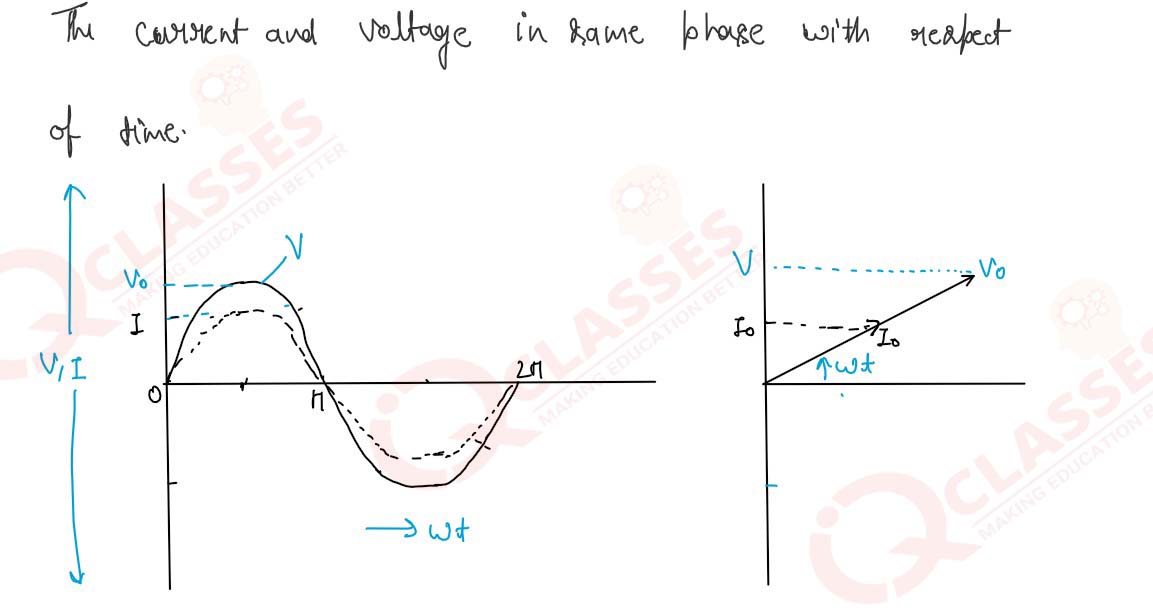
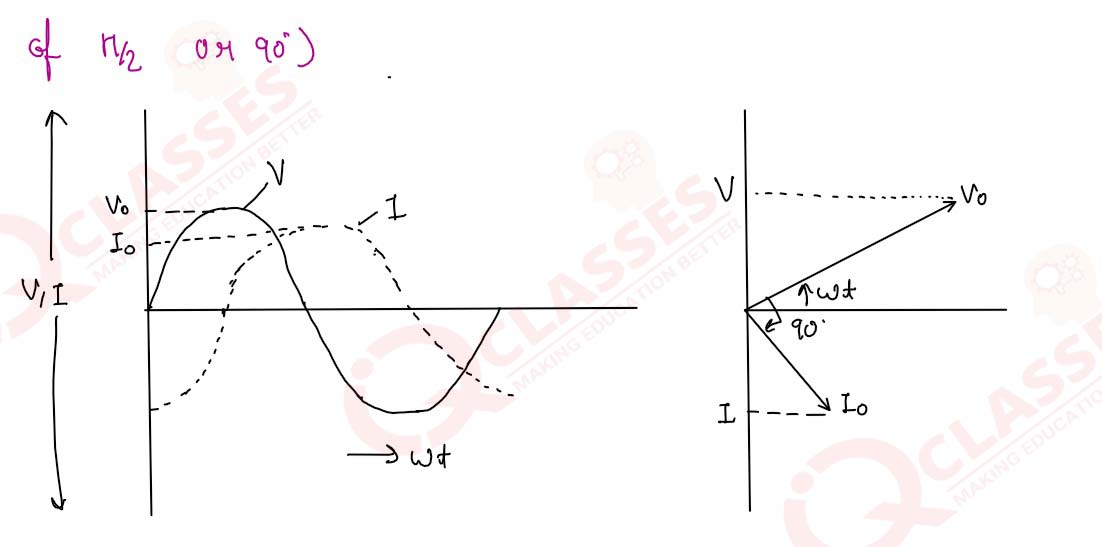
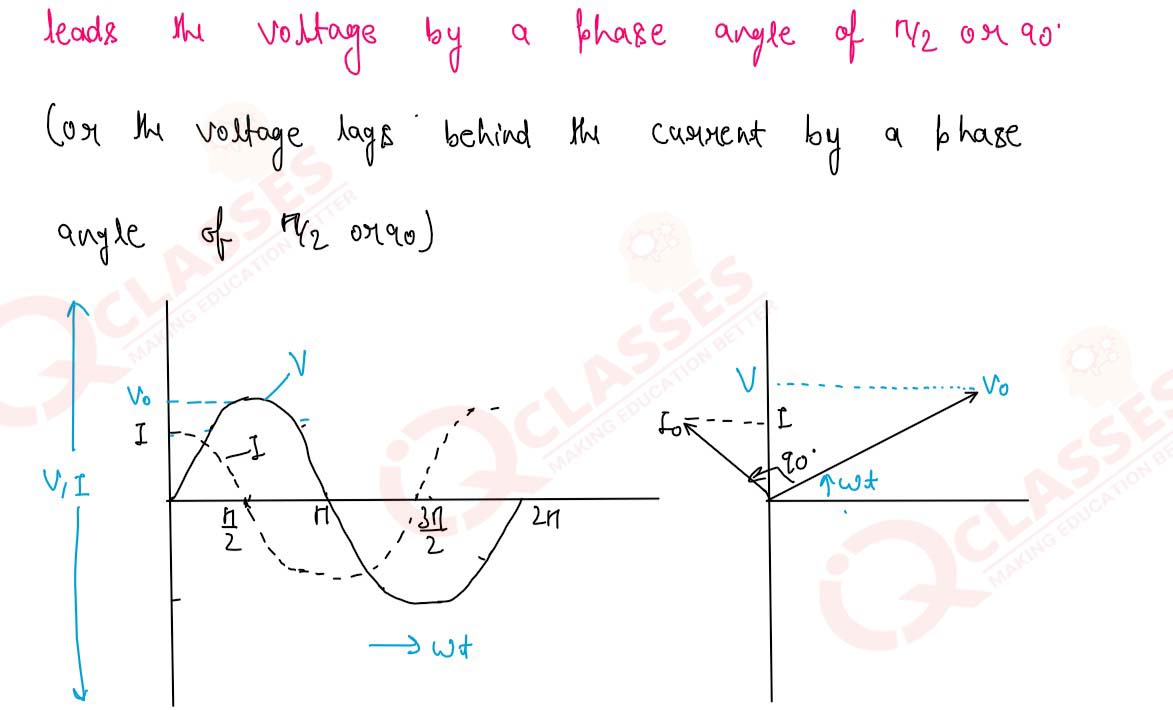
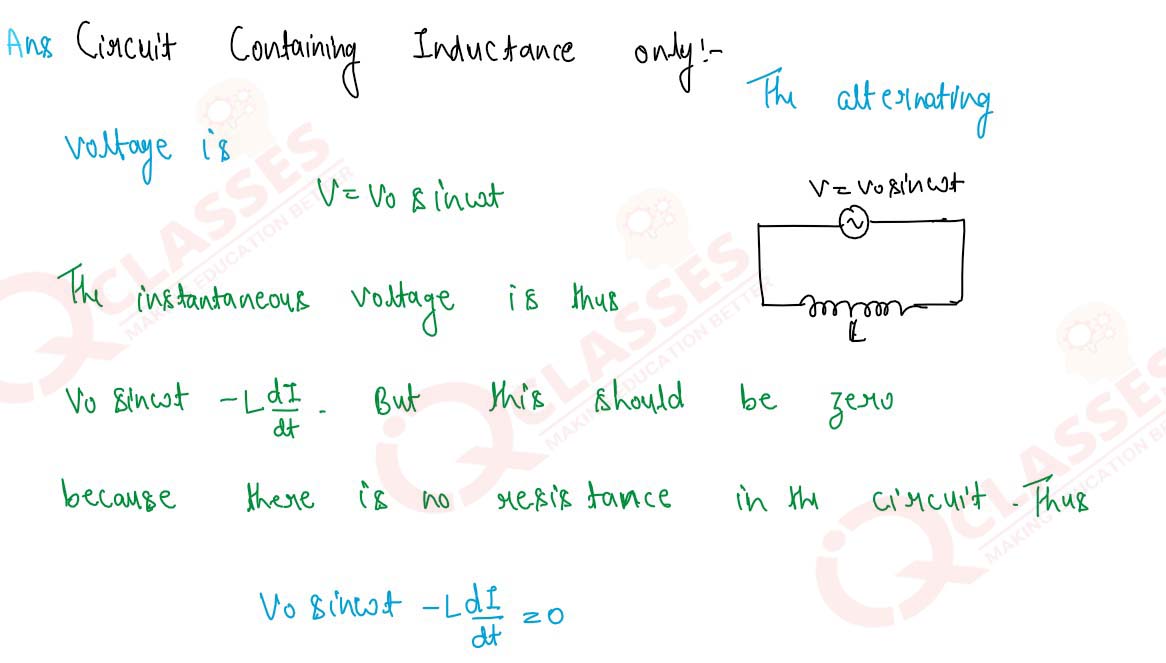
6 An AC emf V = V_{o sin wt is applied across a pure inductance L. Obtain expressions for (i) the
current I
and (ii) the inductive reactance X_L in the circuit. Draw a phasor diagram showing emf
V_o,
current l_o and
their phase difference.} Solution

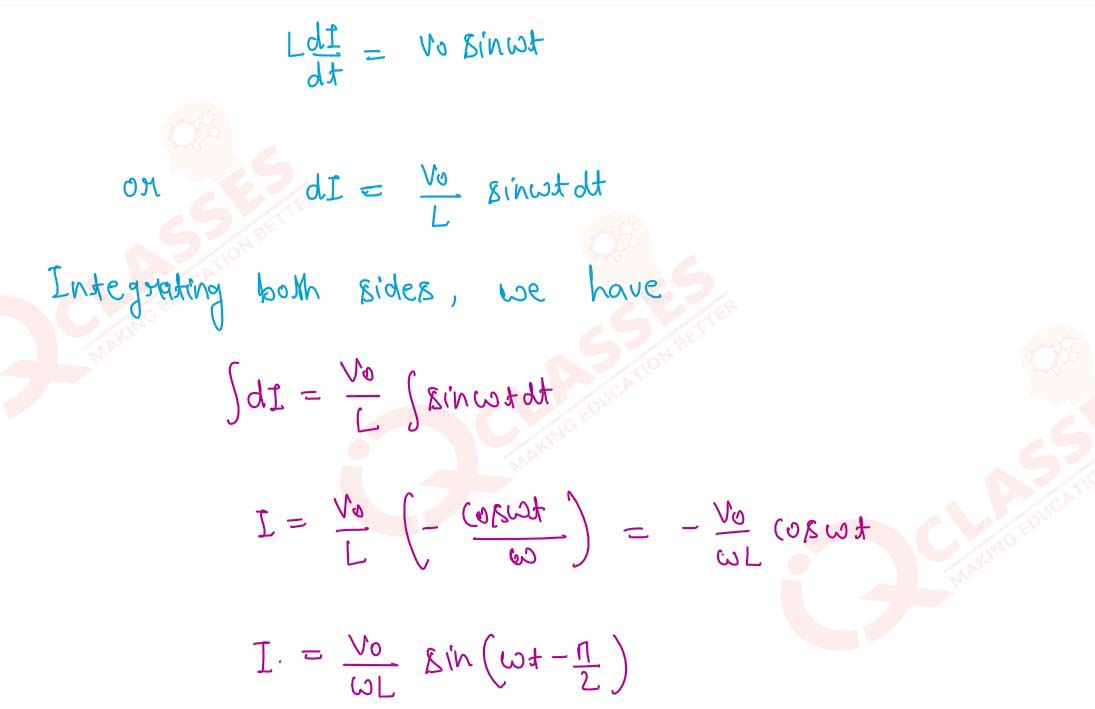
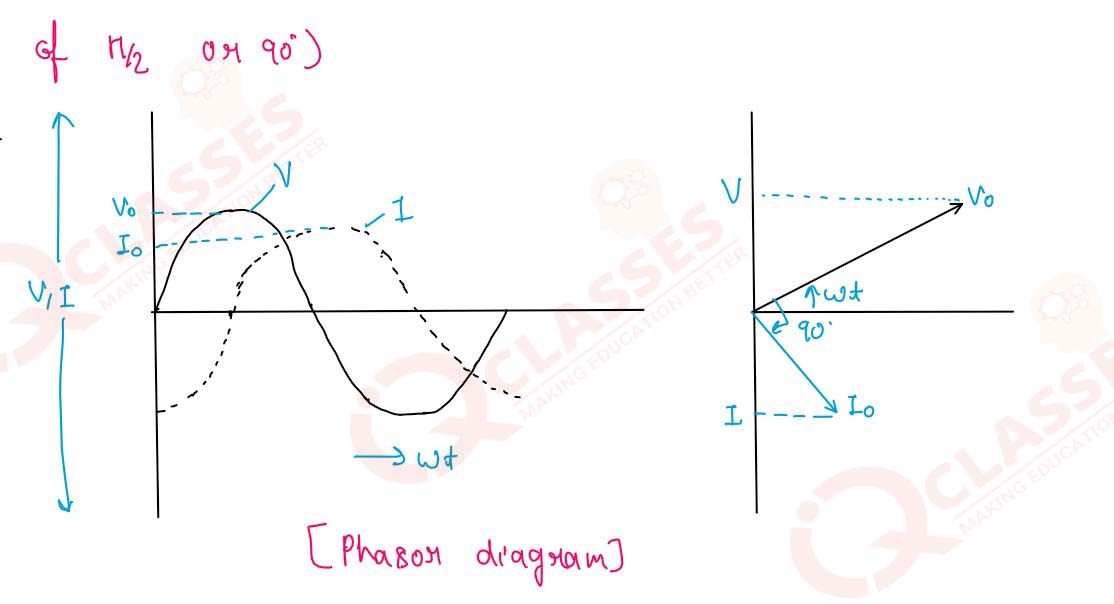
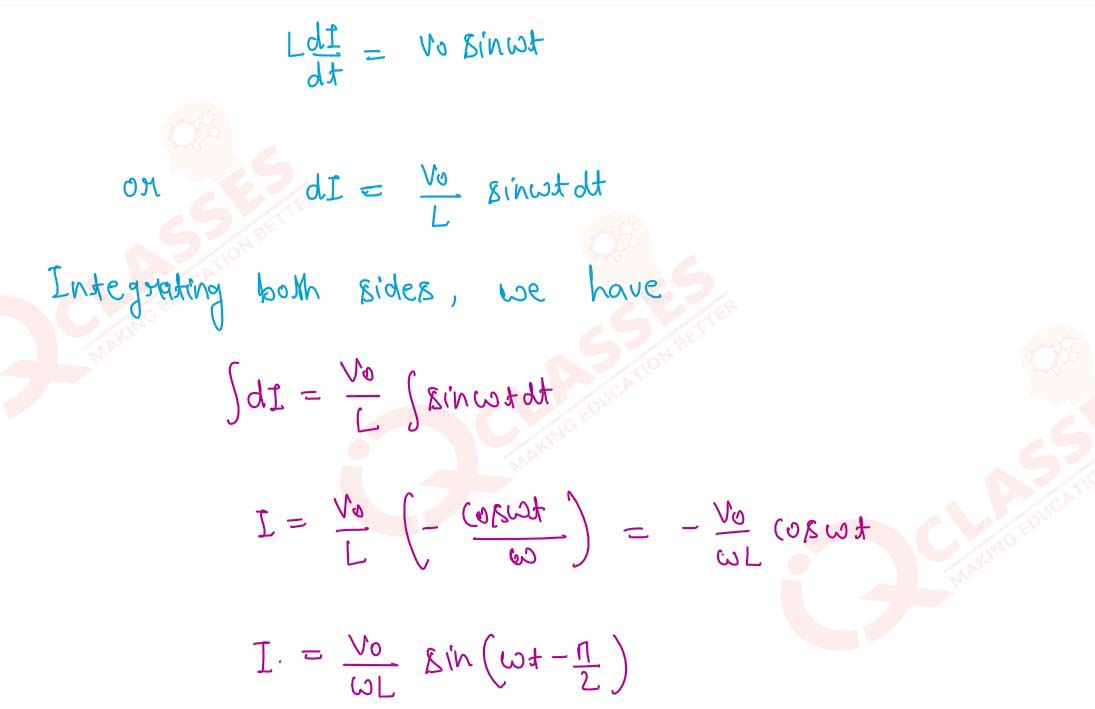
7 Explain the meaning of ‘reactance’.Derive expression for the reactance of an inductor L connected across an AC source. Give its unit. Show that no power is dissipated in an inductor when AC passes through it. Solution

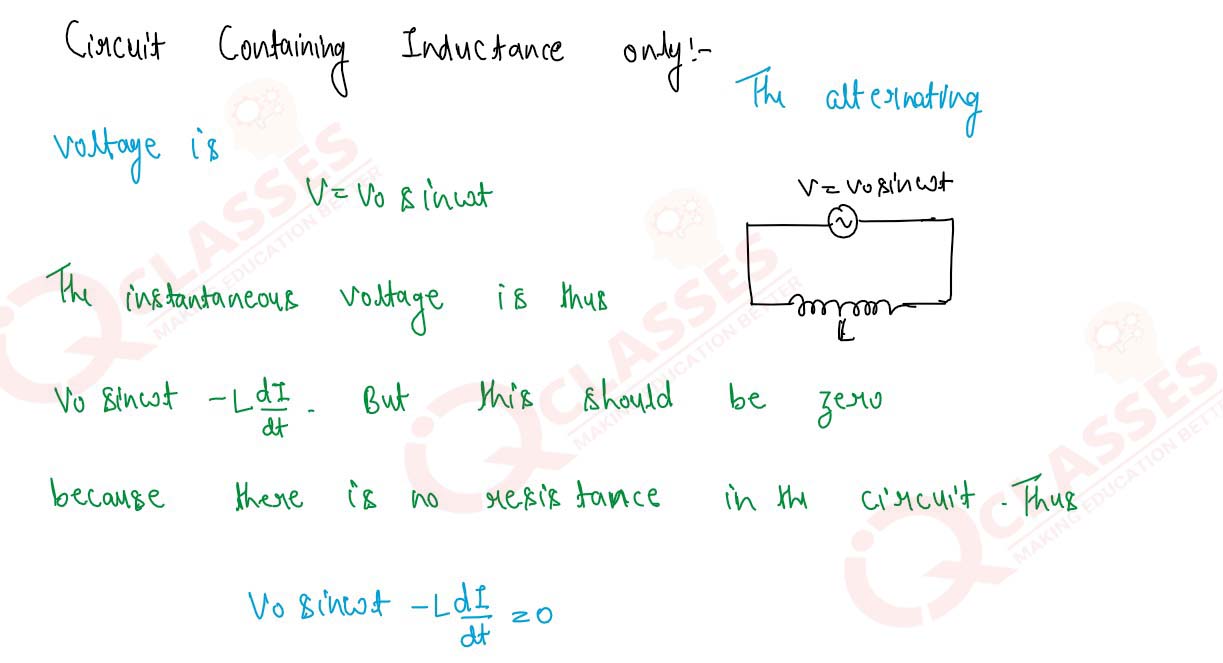
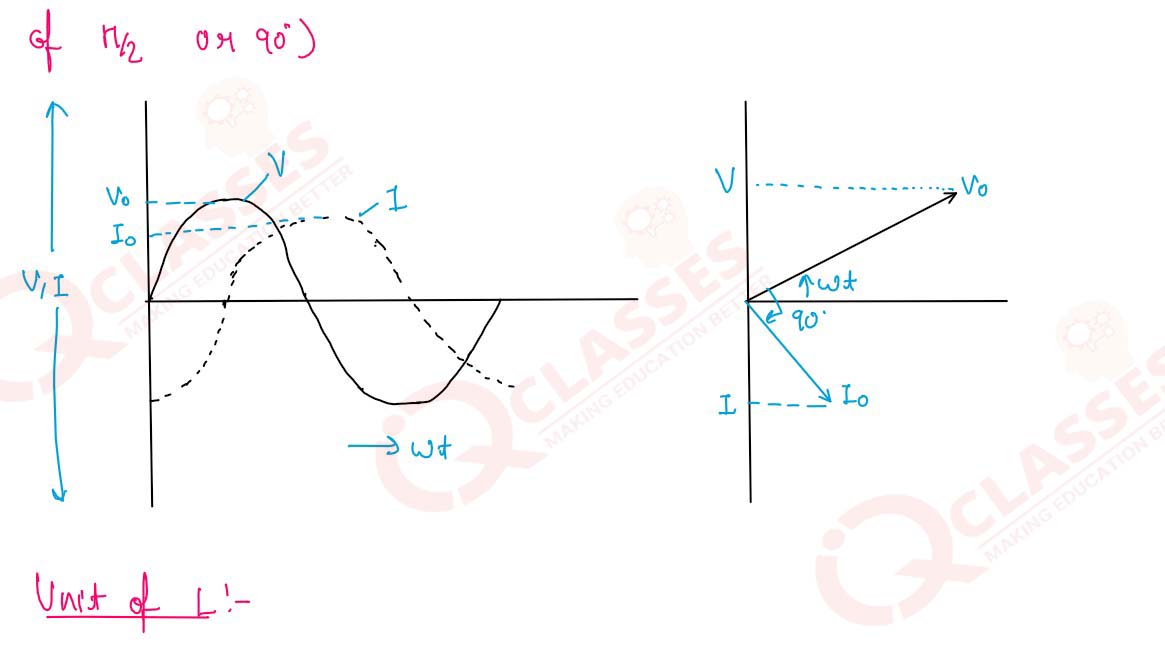
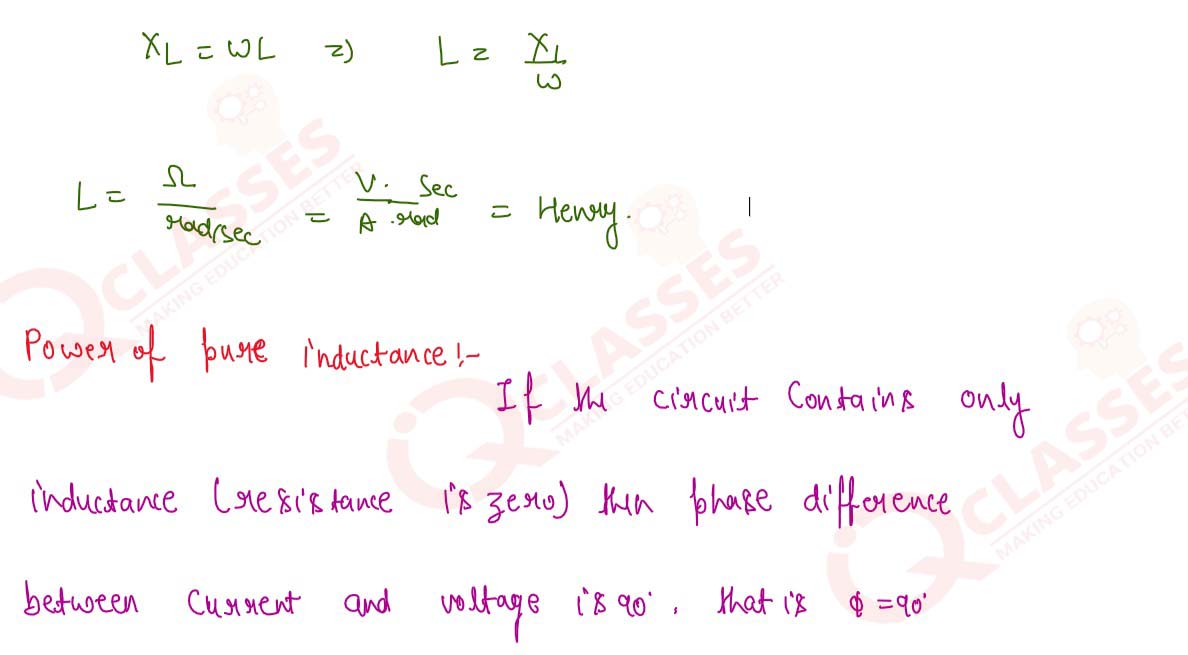
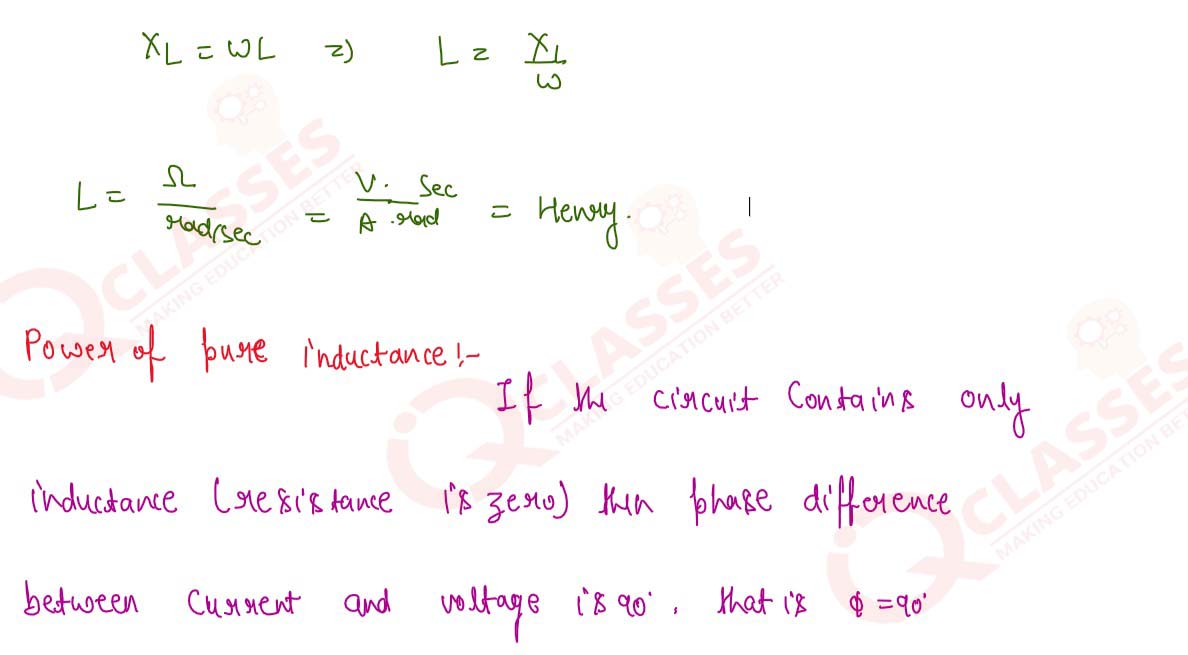
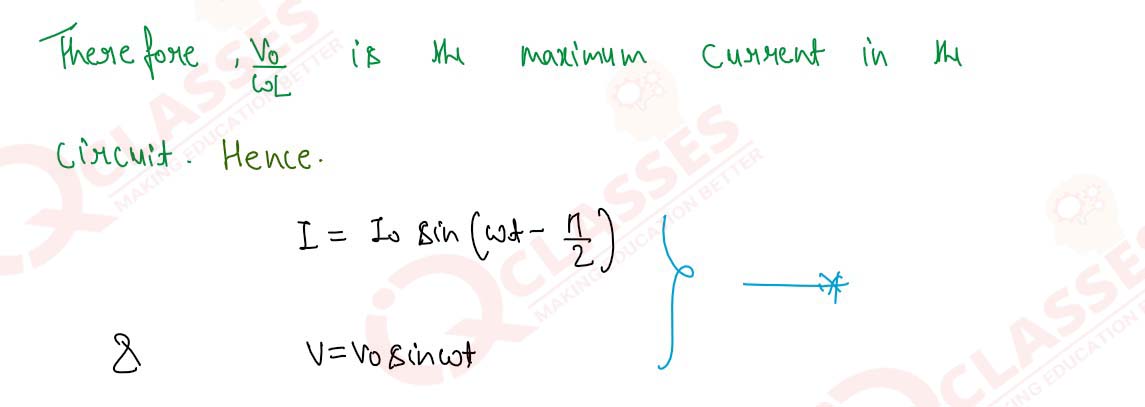
8 Obtain the relation I=I₀ sin (wt + π/2) for a pure inductor across which an alternating emf V=V_o sin wt is applied. Solution

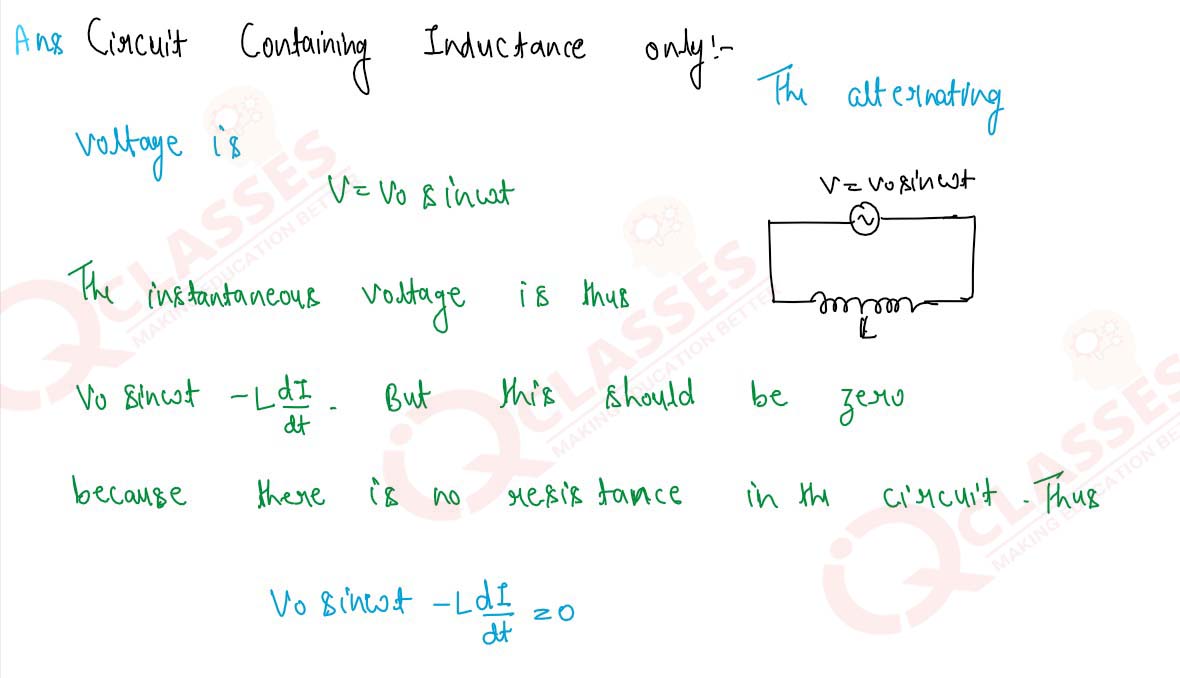
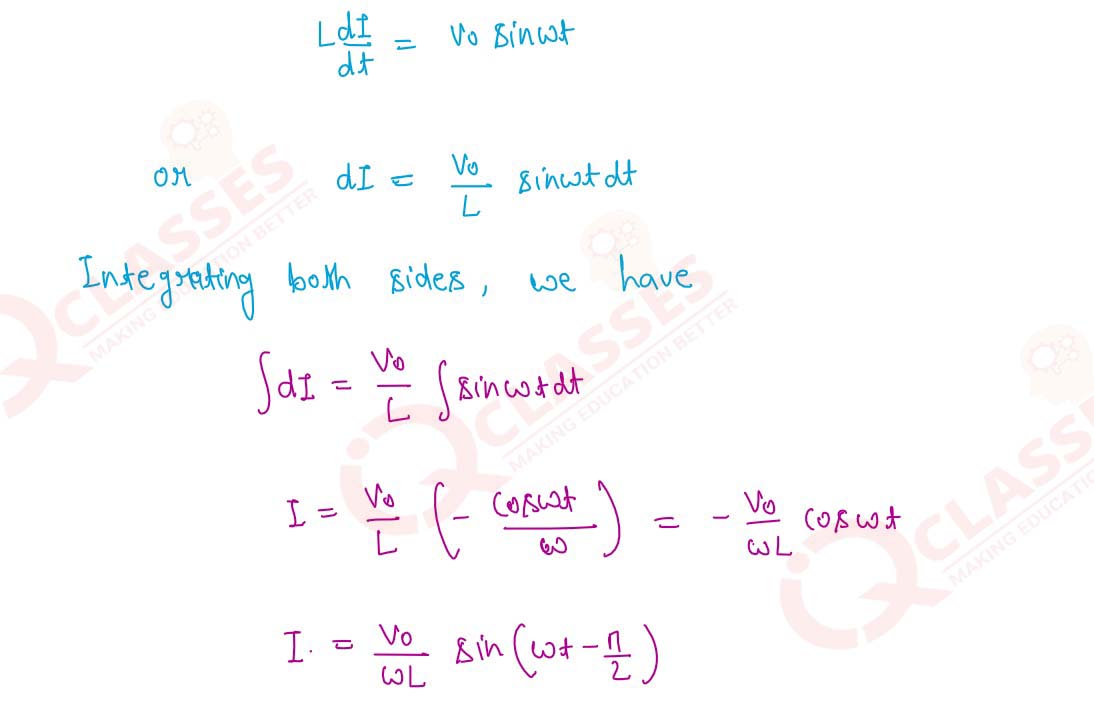
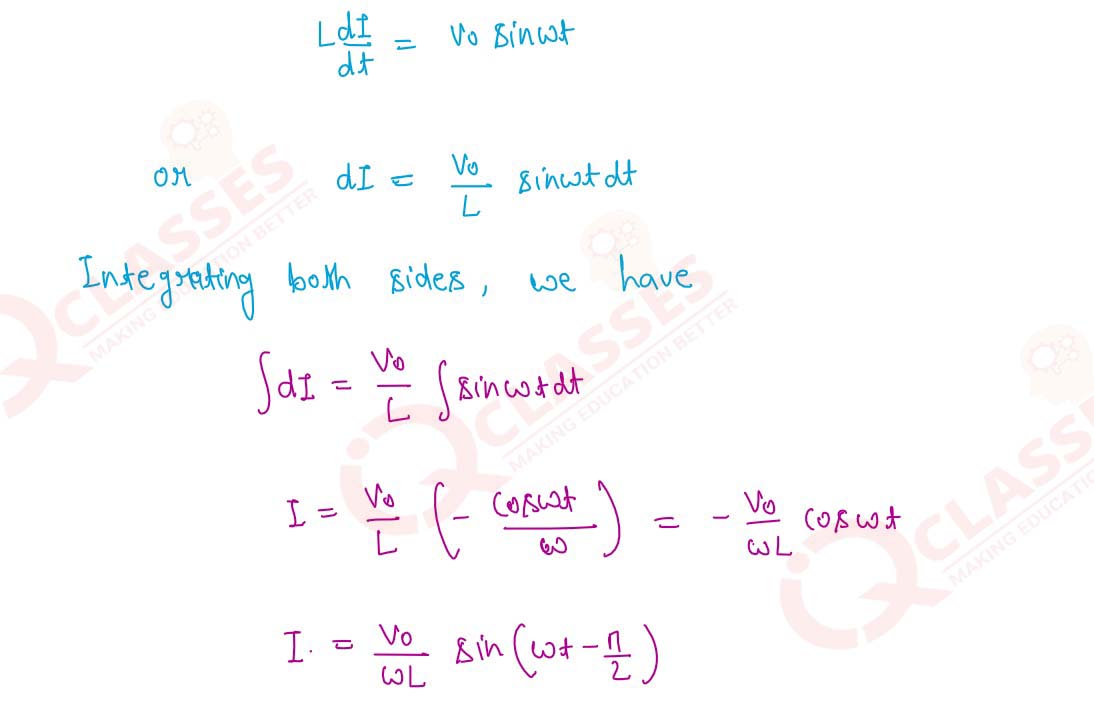
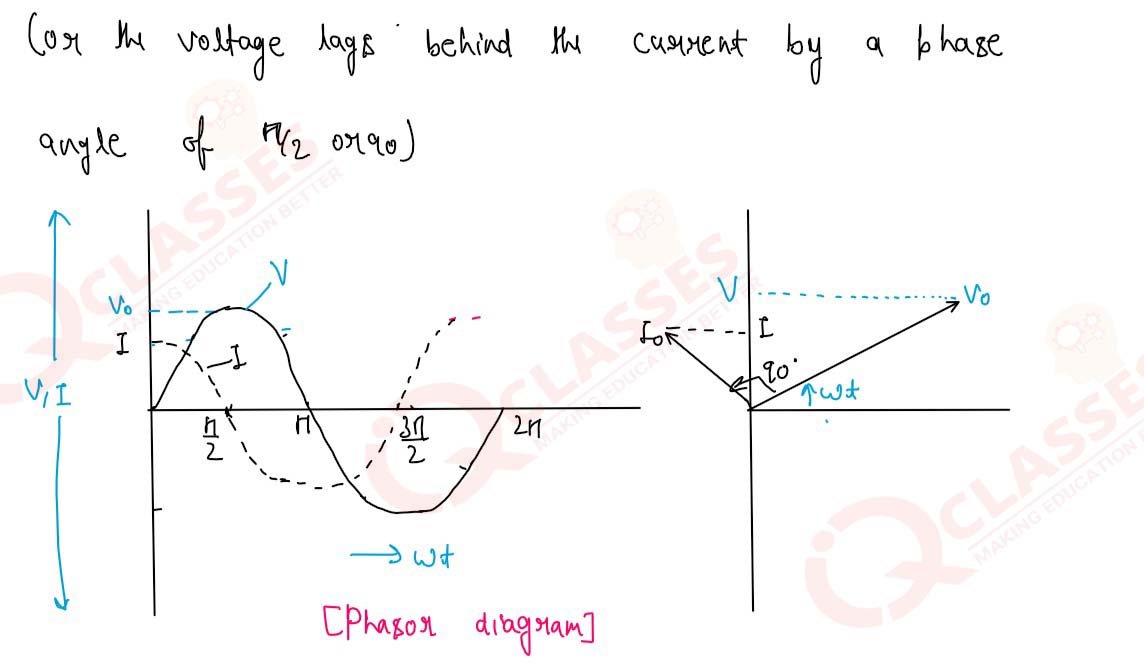
9 Obtain the relation I=I_o sin (wt + π/2) and X_c=1/wC for a pure capacitor across which an alternating emf V=V_o sin wt is applied. Draw a phasor diagram showing emf V, current I and their phase difference. Solution

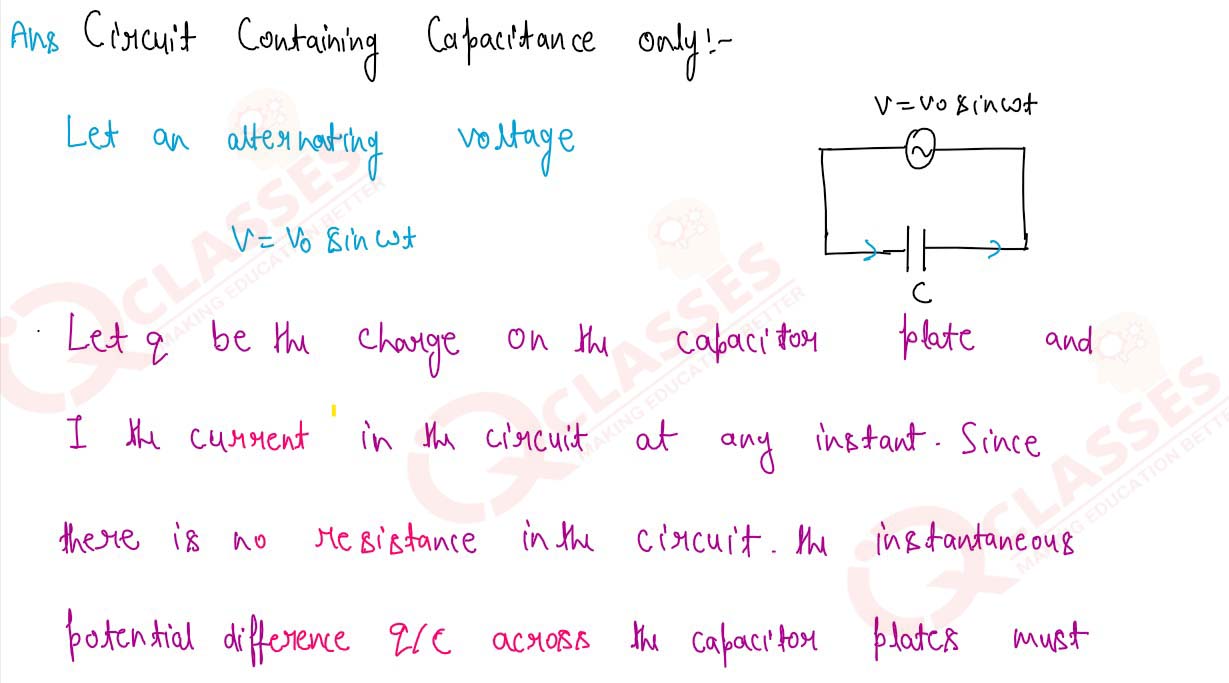
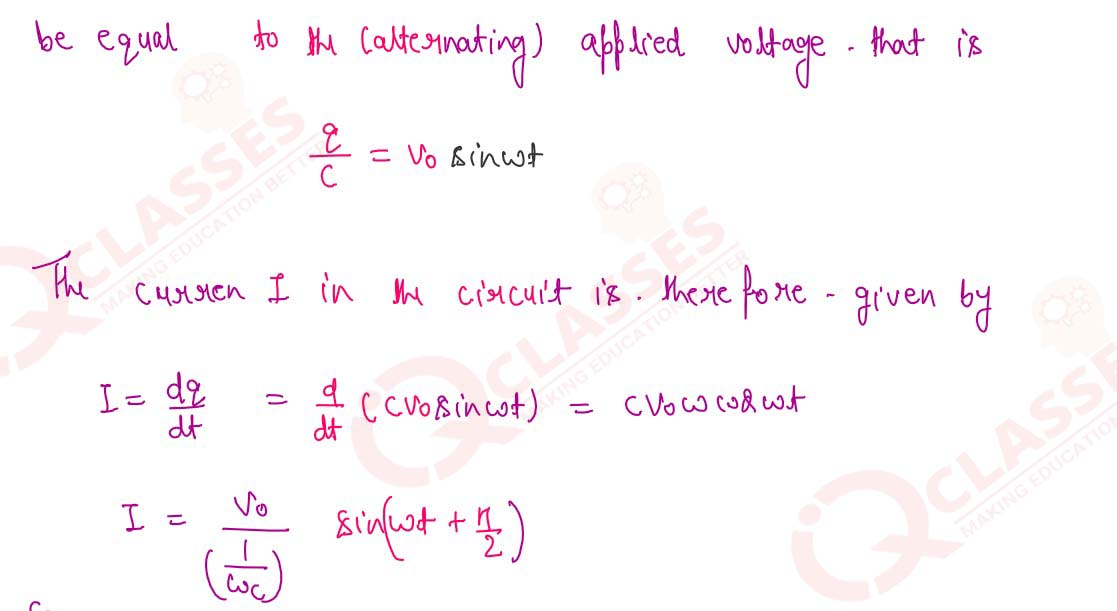
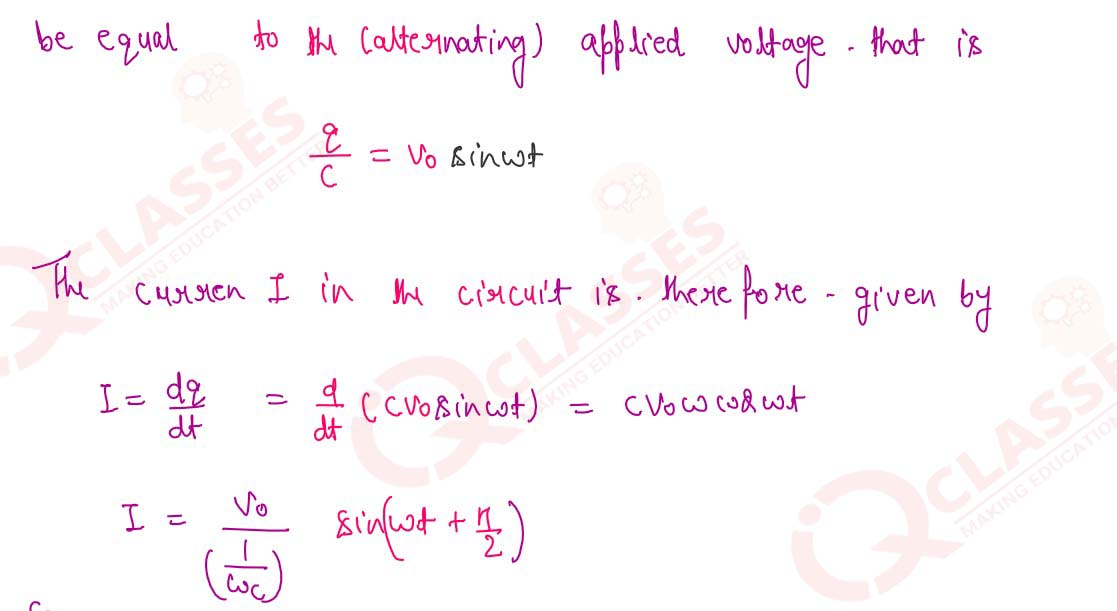
10 A capacitor C is connected to an AC voltage source V=V_o sin wt. Draw a circuit diagram for it. Obtain an expression for the current I flowing in the circuit. Express it as a sin function. What is the phase difference between current I and voltage V? What is the reactance of the capacitor? Solution

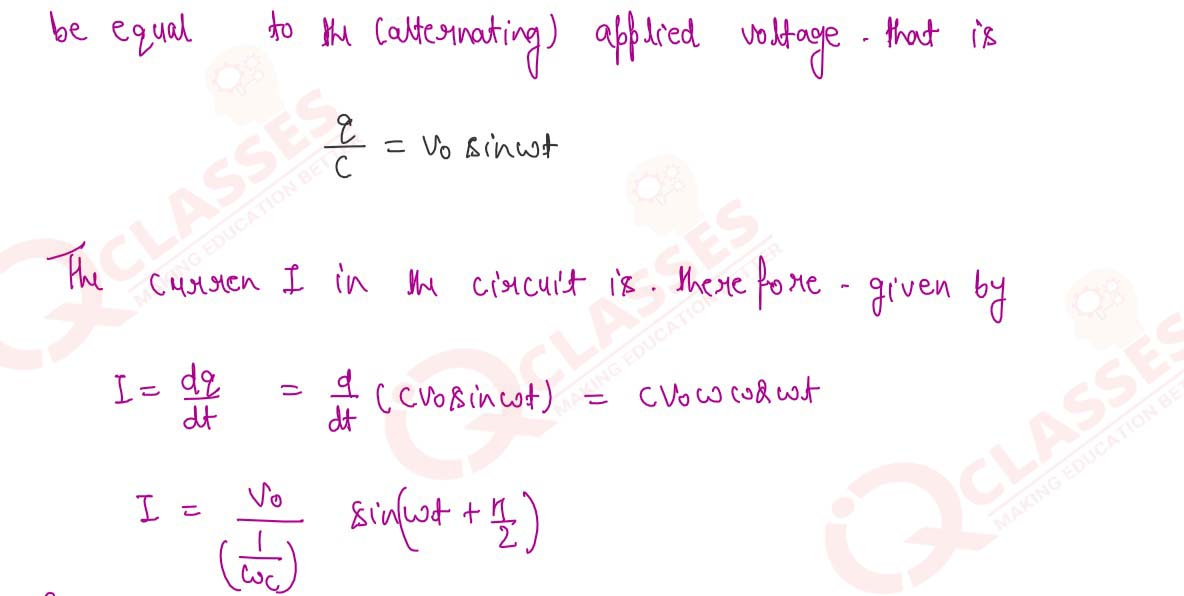
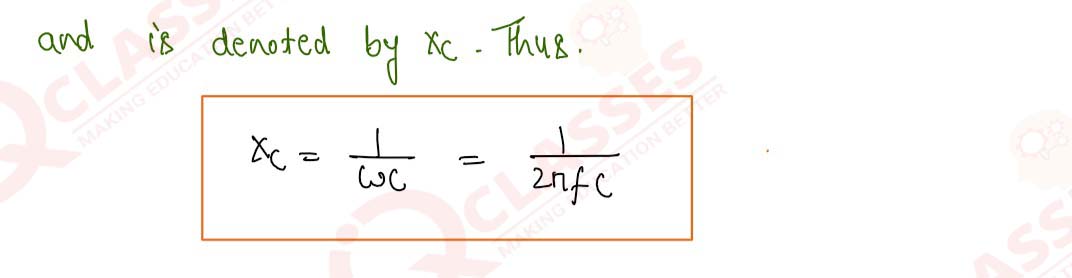
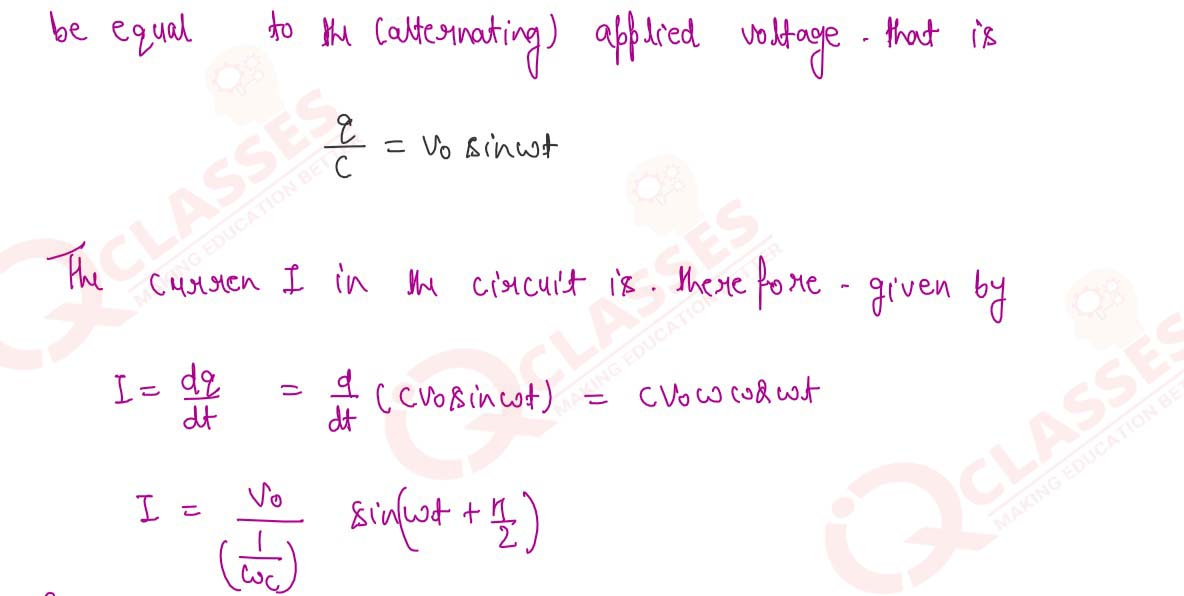
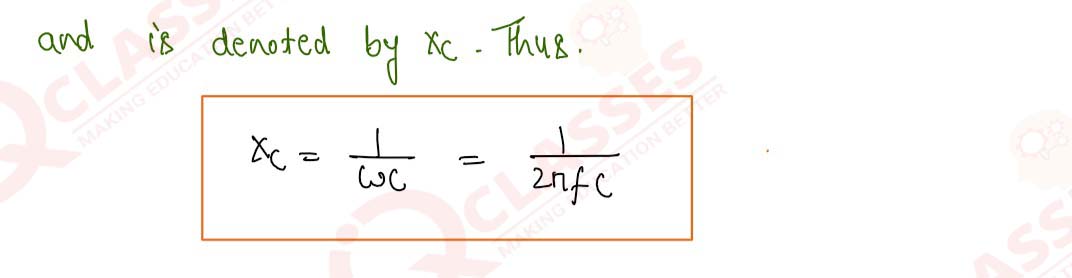
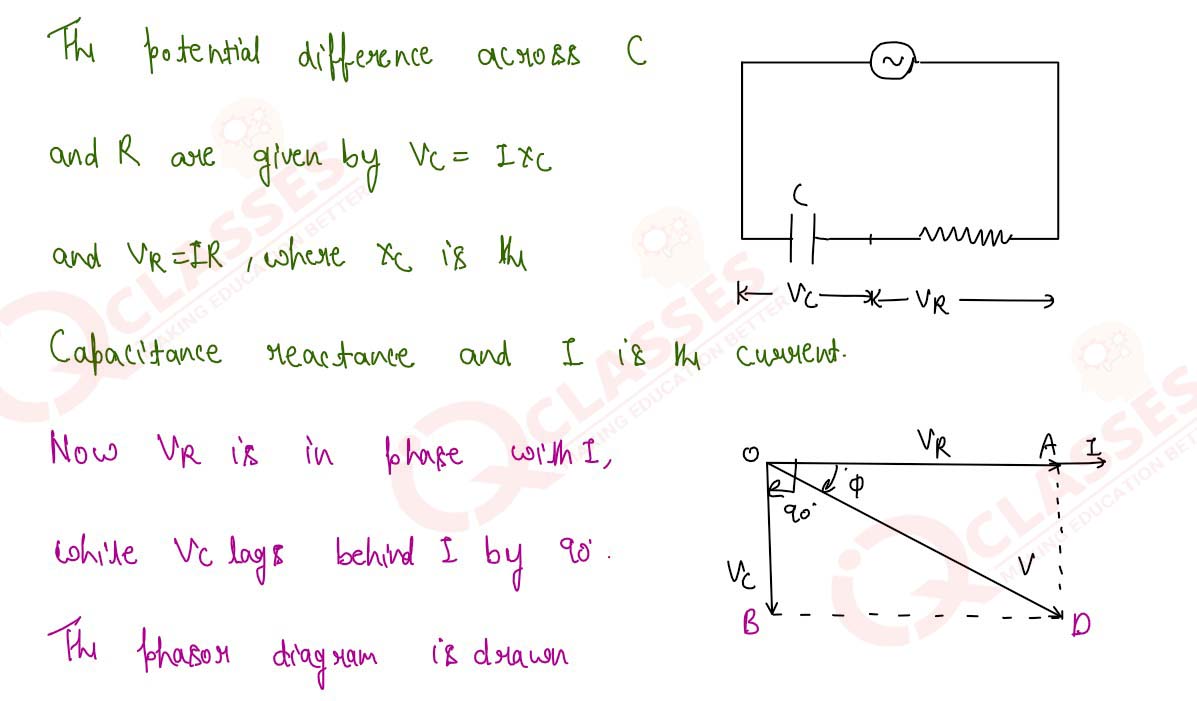
11 What is impedance of an AC circuit? A capacitor C and a resistor R are connected in series in an AC circuit. Derive expression for the impedance Z of the circa Draw phasor diagram. Solution

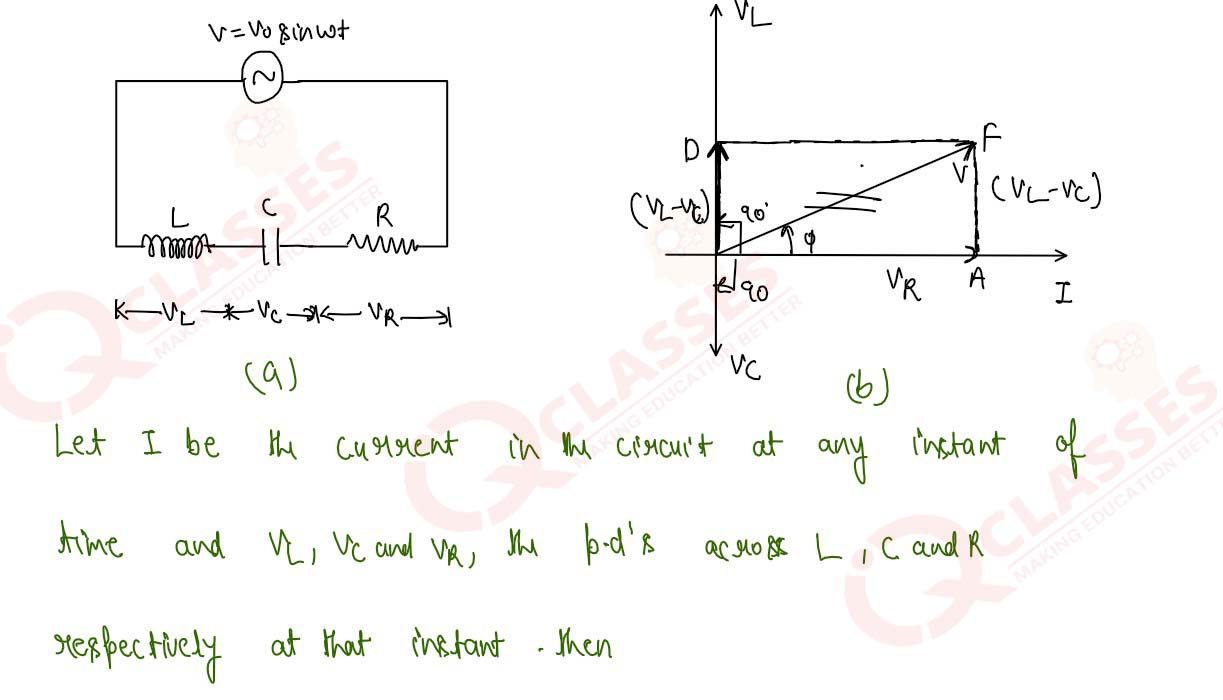
12 In an alternating-current circuit an inductance L, capacitance C and a resistance R are connected in series. Derive expression for the impedance and the phase angle. What is the impedance at resonance? Solution

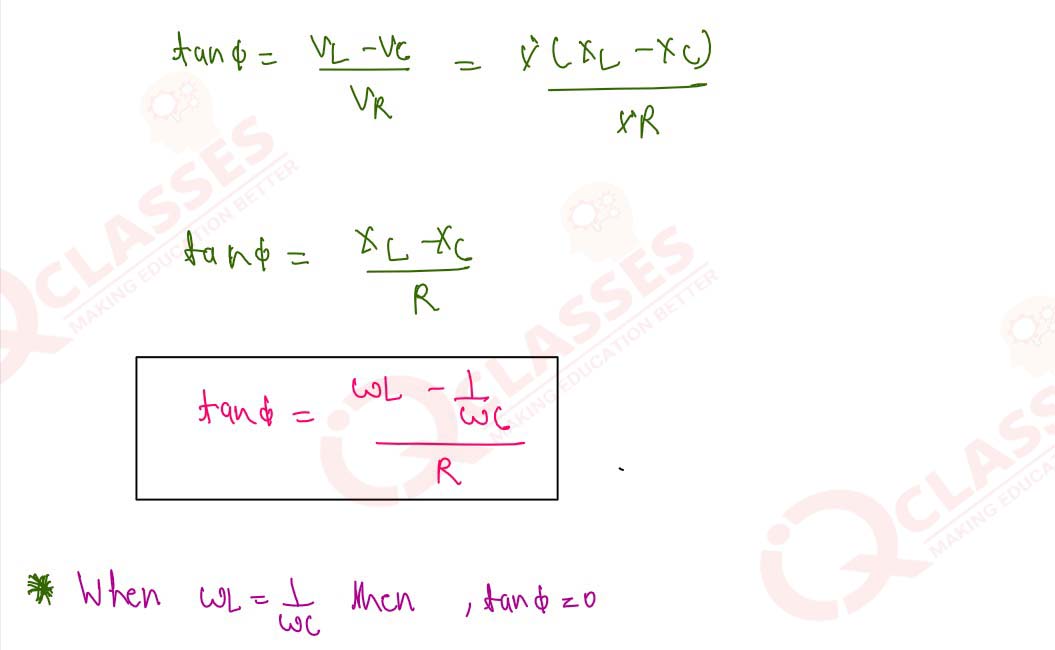
13 Derive an expression for the phase angle of an AC circuit with an inductor L, a capacitor C and a resistor R in series. Draw the phasor diagram if the voltage across the capacitor is greater than that across the inductor, Obtain an expression for the resonat frequency of the circuit. Solution

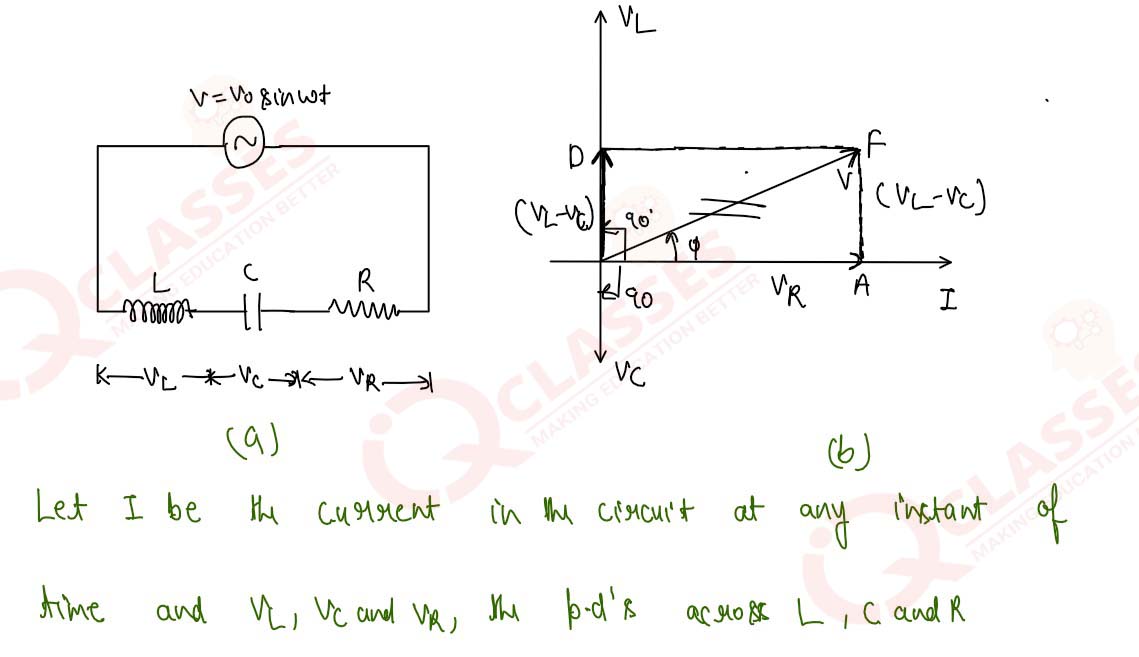
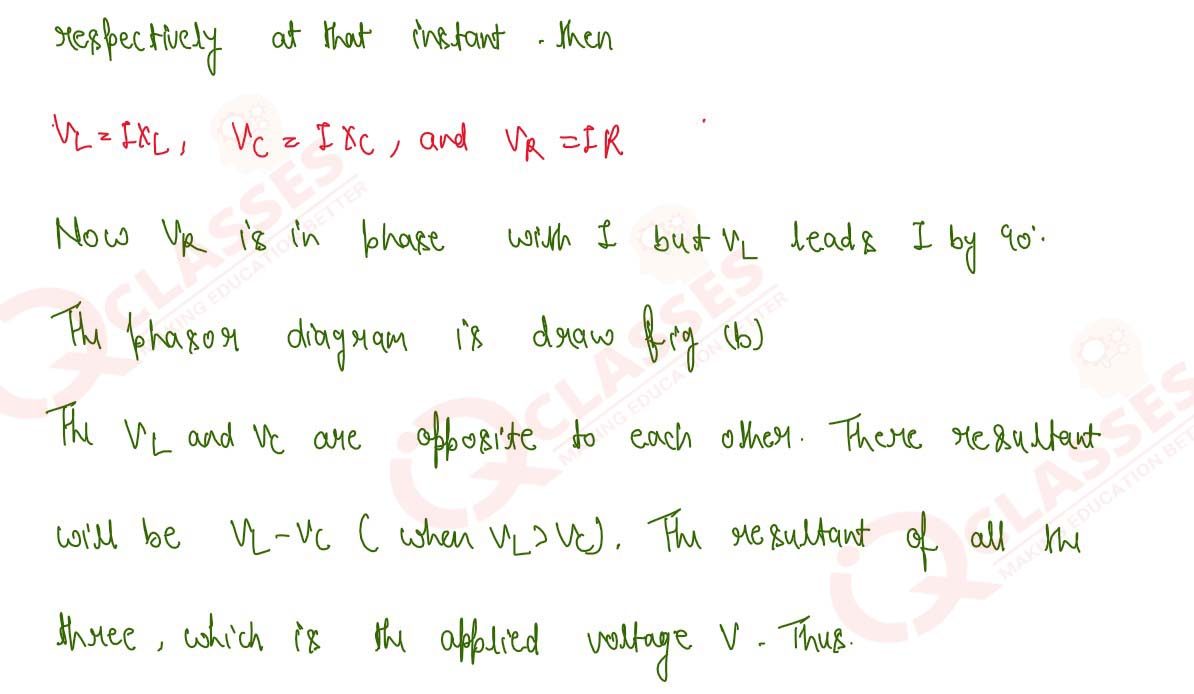
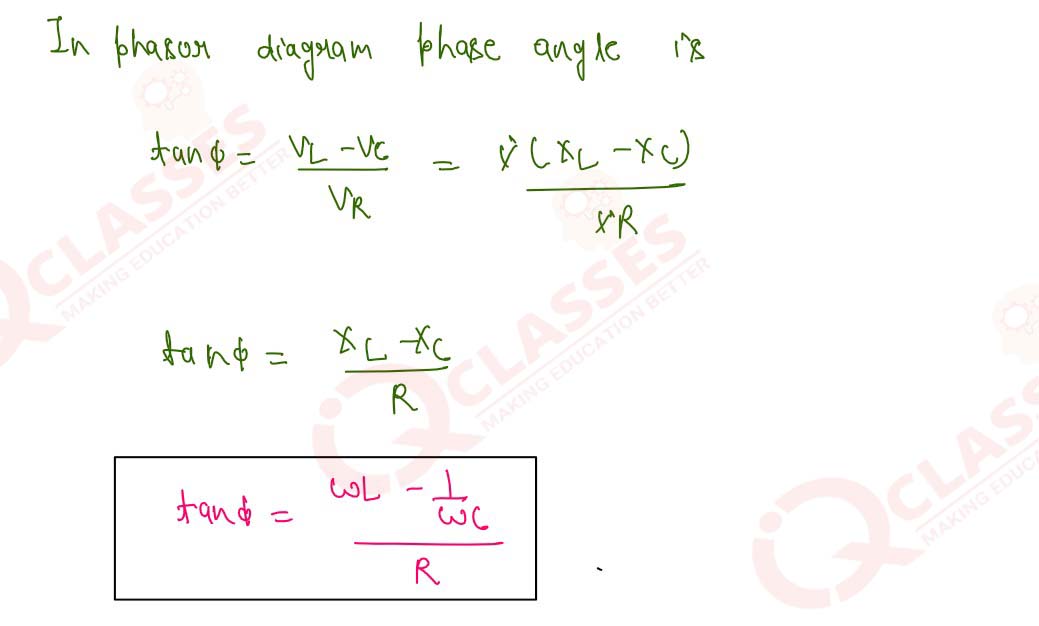
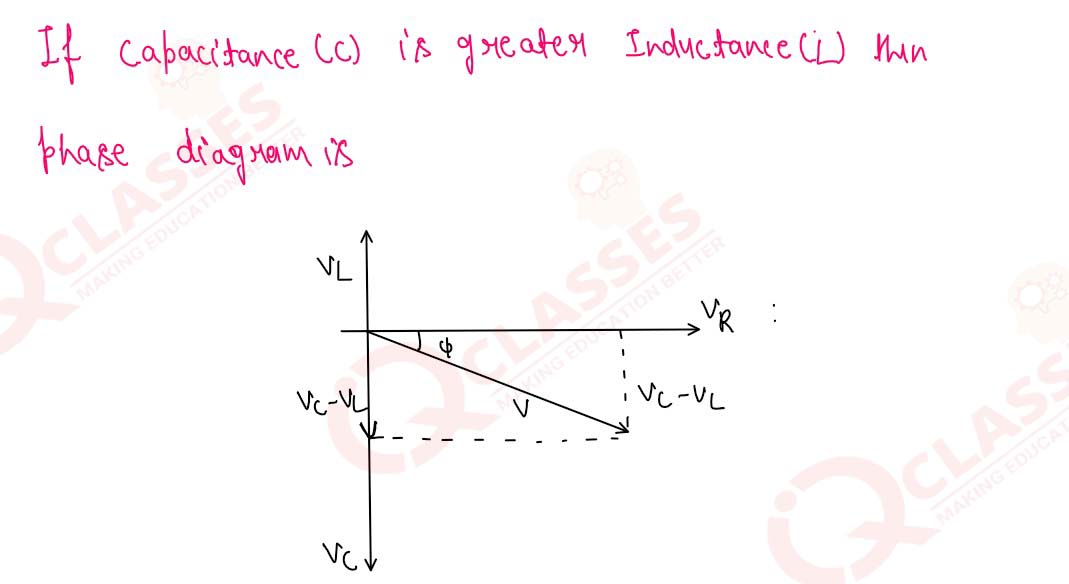
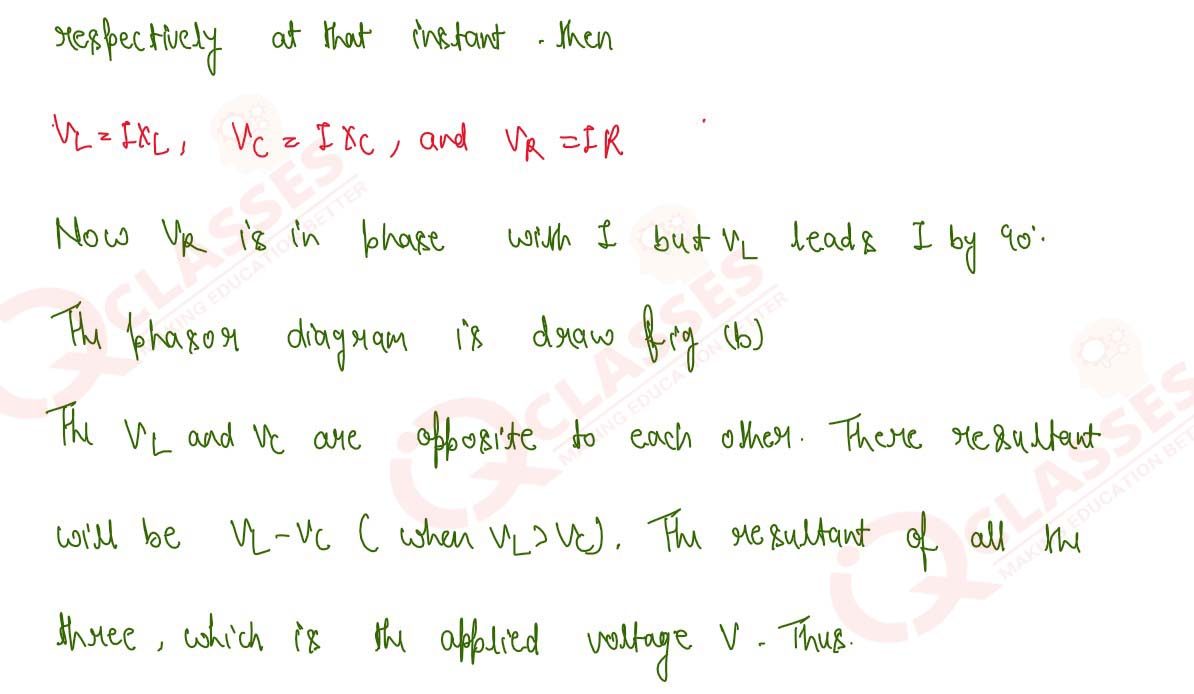
14 Show that the average power dissipated per cycle in an L-C-R circuit is given by P= V_rms I_rms x cos θ, where θ is the angle of lag or lead. Solution

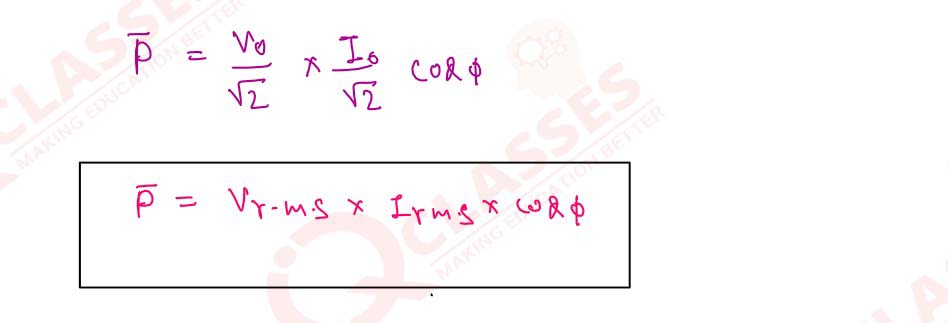
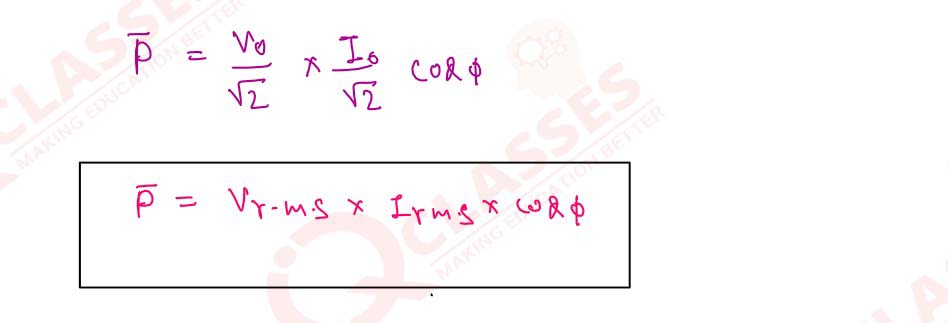
15 Show that the average power dissipated in an AC circuit is, in general, given by

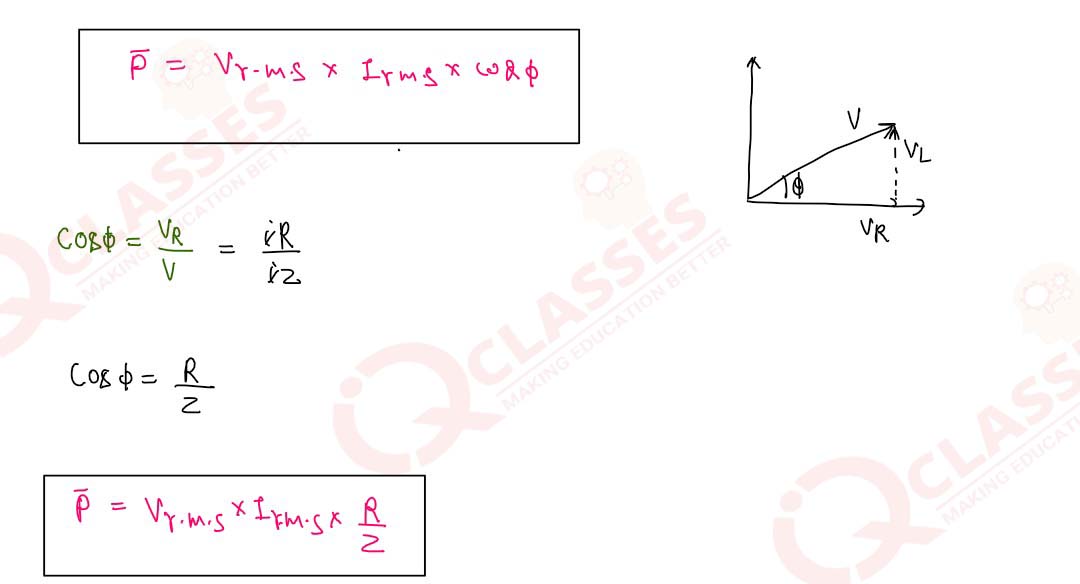
P=V_rms xI_rms xR/Z where R is the resistance of the circuit (defined as real part of the complex impedance) and Z is the impedance. Solution

16 Prove that power dissipated in an ideal resistor connected to an AC source is V_eff²/R. Solution

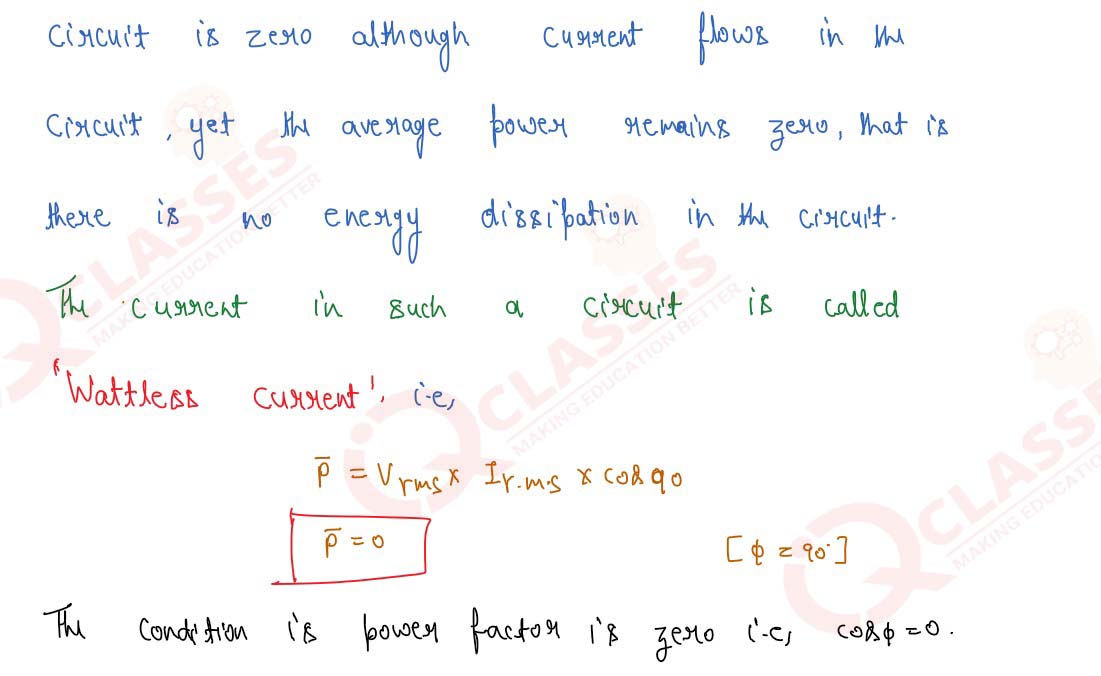
17 What do you understand by 'wattless current'? Why is the current passing in a choke coil wattless? Solution

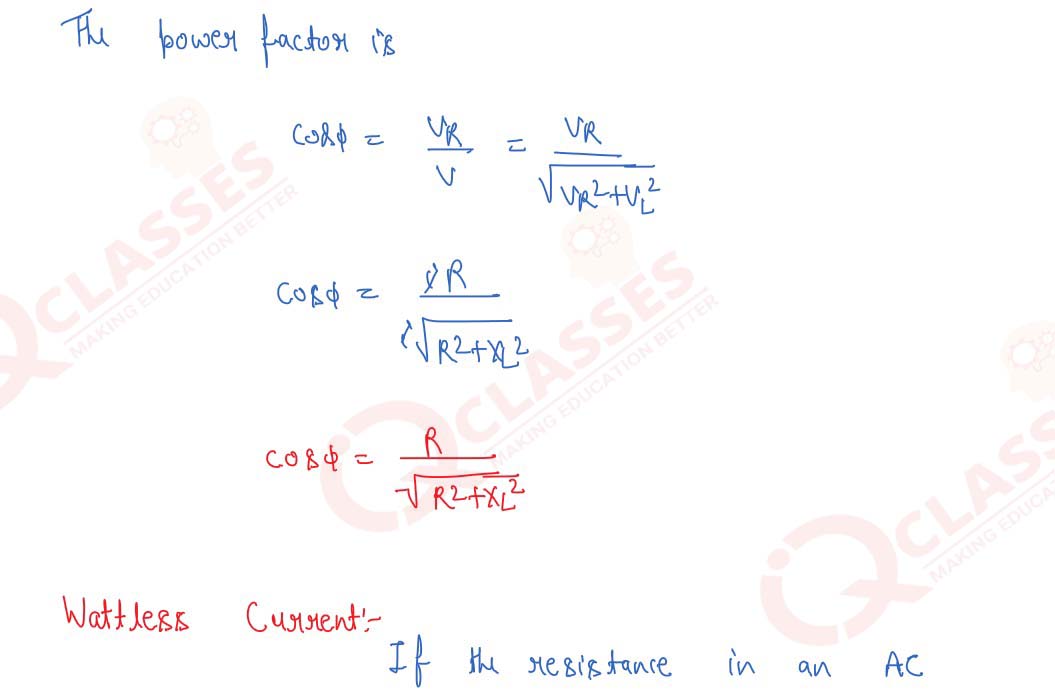
18 Obtain an expression for the power factor of an AC L-R circuit. Give the necessary condition for a wattless current in the circuit. Solution

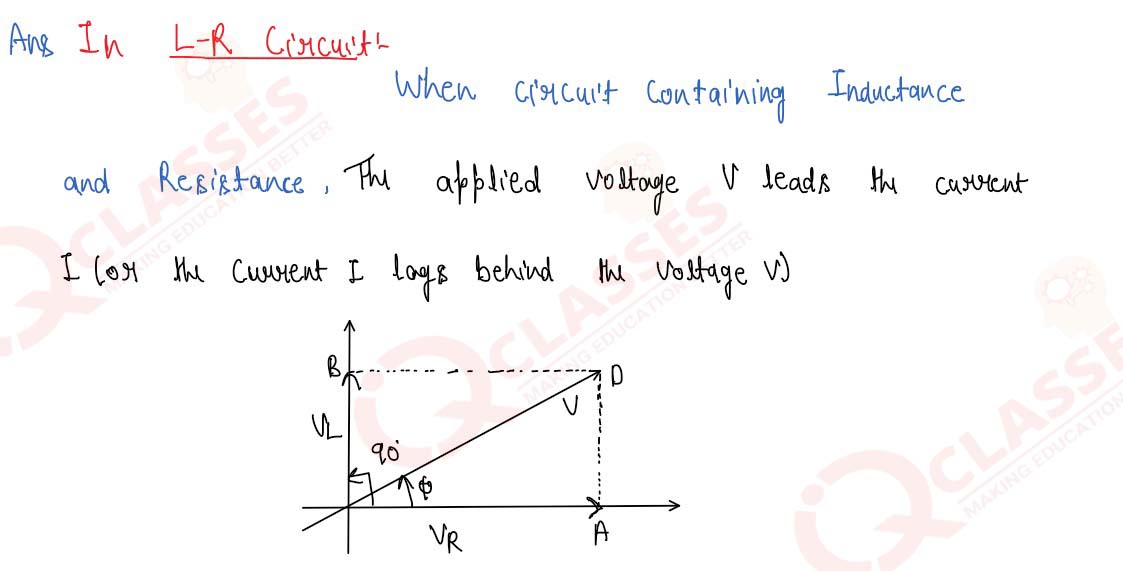
19 Prove that an ideal inductor does not dissipate power in an AC circuit. Solution

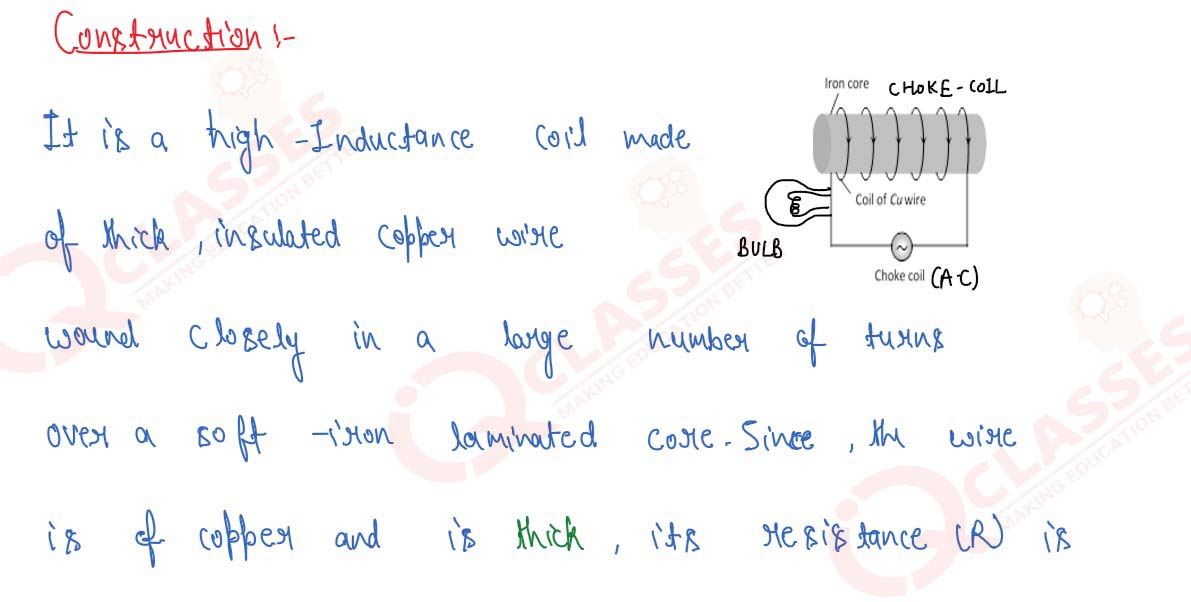
20 Explain the principle, construction and working of a choke coil in controlling current in an AC circuit. Why is it preferred to resistance in AC circuits? Solution

21 Discuss the phenomenon of resonance in an L-C-R series AC circuit. Solution

22 Obtain an expression for resonant frequency fo of a series L-C-R circuit Solution

23 In series L-C-R circuit, obtain an expression for the resonant frequency Solution