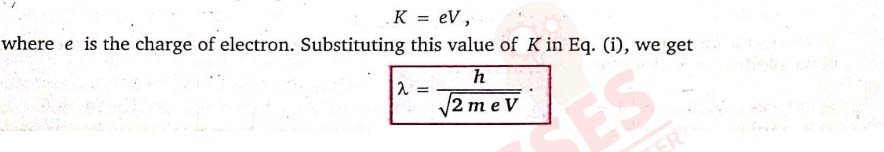Q1
solutions
In 1924, French physicist de-Broglie introduced a bold hypothesis that if radiation has a dual (wave- particle) nature, the moving particles of matter (electrons, protons, etc.) should exhibit wave-like character under appropriate conditions. He reached this conclusion on the observation that the entire universe is composed of matter and (electromagnetic) radiation, and that nature loves symmetry. These two physical entities, matter and radiation, must have symmetrical character.

the wavelength computed from de-Broglie hypothesis, shows that electrons are wave like in some circumstances. Other fundamental particles like neutrons also show wave like properties. The Davisson-Germer experiment thus provided direct verification of de-Broglie hypothesis of the wave-nature of moving particles.
- What is de-Broglie hypothesis?
- What conclusion can be drawn from Davisson and Germer's experiment?
solutions

In 1924, French physicist de-Broglie introduced a bold hypothesis that if radiation has a dual (wave- particle) nature, the moving particles of matter (electrons, protons, etc.) should exhibit wave-like character under appropriate conditions. He reached this conclusion on the observation that the entire universe is composed of matter and (electromagnetic) radiation, and that nature loves symmetry. These two physical entities, matter and radiation, must have symmetrical character.

the wavelength computed from de-Broglie hypothesis, shows that electrons are wave like in some circumstances. Other fundamental particles like neutrons also show wave like properties. The Davisson-Germer experiment thus provided direct verification of de-Broglie hypothesis of the wave-nature of moving particles.
Q2
Show that the de-Broglie wavelength of electron of energy K is given by λ=h/√2mK.
solutions de-Broglie Wavelength of Electron
Let us consider an electron of mass m moving with velocity v (much smaller than the velocity of light). Its de-Broglie wavelength is given by

This is, however, a general expression for the de-Broglie wavelength of a moving particle in terms of the kinetic energy of the particle.
solutions de-Broglie Wavelength of Electron
Let us consider an electron of mass m moving with velocity v (much smaller than the velocity of light). Its de-Broglie wavelength is given by

This is, however, a general expression for the de-Broglie wavelength of a moving particle in terms of the kinetic energy of the particle.
Q3
Show that the de-Broglie wavelength of electrons accelerated through a potential of V volt is given
by λ=h/√2meV
solutions de-Broglie Wavelength of Electron
Let us consider an electron of mass m moving with velocity v (much smaller than the velocity of light). Its de-Broglie wavelength is given by

This is, however, a general expression for the de-Broglie wavelength of a moving particle in terms of the kinetic energy of the particle. Let us now come to the particular case of electron. If the electron acquires kinetic energy on being accelerated from rest through a potential difference of V volt, then
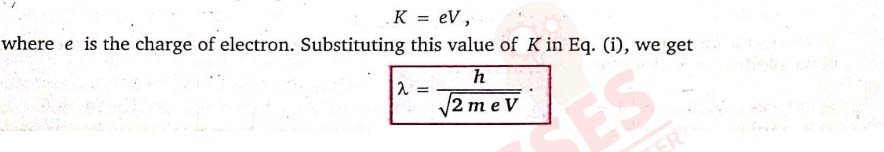
solutions de-Broglie Wavelength of Electron
Let us consider an electron of mass m moving with velocity v (much smaller than the velocity of light). Its de-Broglie wavelength is given by

This is, however, a general expression for the de-Broglie wavelength of a moving particle in terms of the kinetic energy of the particle. Let us now come to the particular case of electron. If the electron acquires kinetic energy on being accelerated from rest through a potential difference of V volt, then