Q1
Explain work function and threshold frequency in photoelectric emission. Give Einstein's equation
for photoelectric emission. What do the symbols stand for?
solutions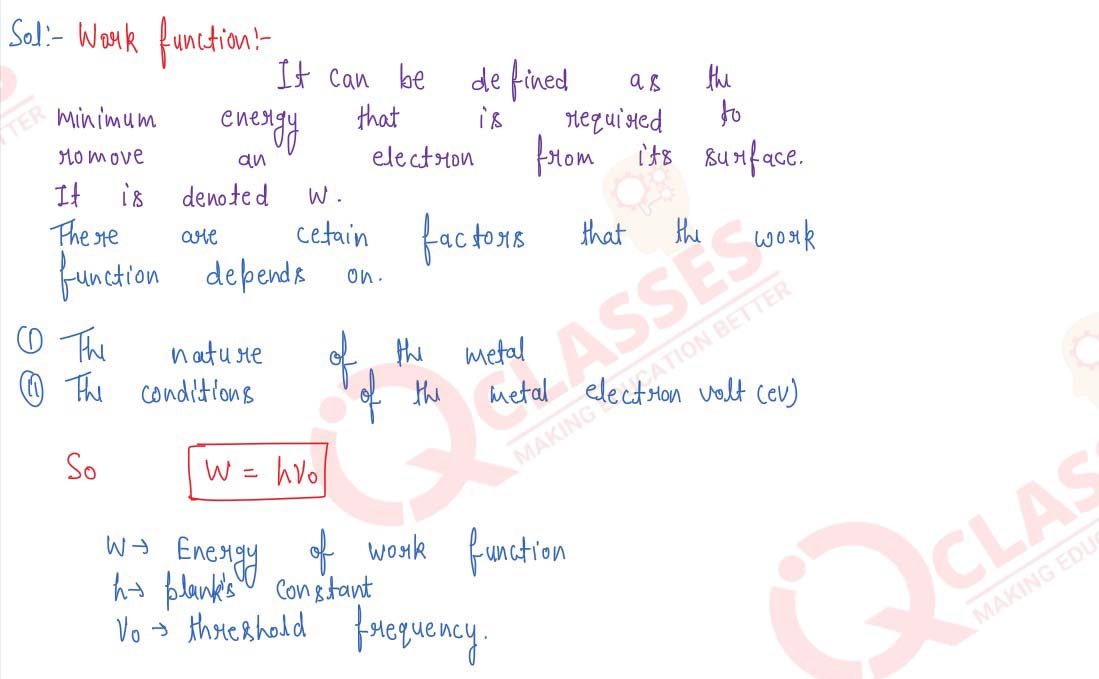
solutions
Q2
Draw a graph between the frequency of light used for photoelectric effect and the maximum kinetic
energy of the emitted photoelectrons. Explain:
solutions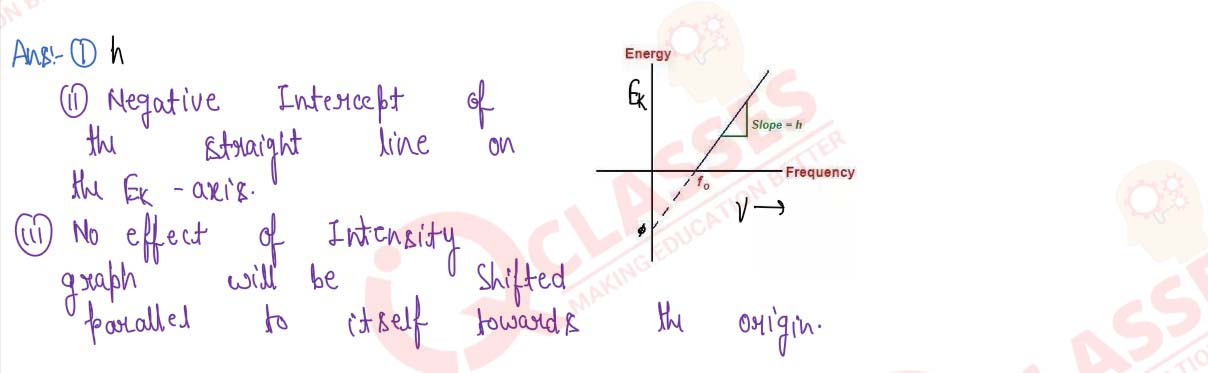
- What does the slope of the graph represent?
- How is the work function of the metal surface obtained by the graph?
- What will be the effect on the nature of the graph, if the intensity of the incident light be doubled, or metal of lower work function be taken?
solutions
Q3
State the dependence of work function on the kineric energy of the electrons emitted in a photocell.
If the intensity of incident radiation is doubled, what changes occur in the stopping potential,
kinetic energy of the photoelectrons and the photoelectric current?
solutions
solutions
Q4
Establish the Einstein's equation
and explain the laws of photoelectric effect on its basis.
solutions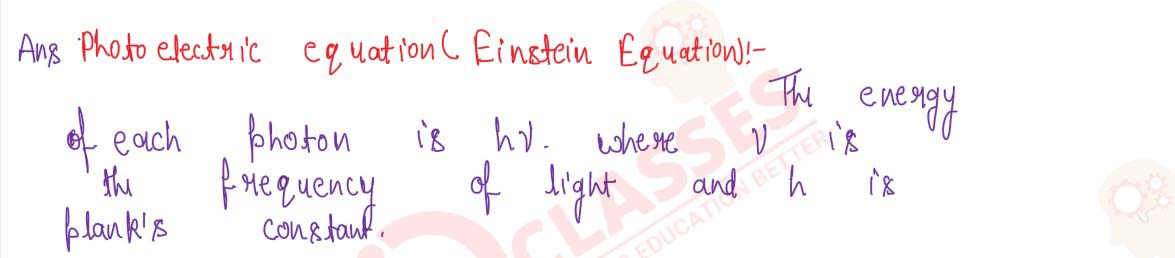
suppose, the (maximum) kinetic energy of photoelectrons emitted from the metal-surface is
Ek and W is
the energy required to eject a photoelectron from the metal. W is the work-function of the metal.
Then,
according to the above explanation, we have
hv=W+Ek
Ek=hv-W
where h v is the energy of the photon absorbed by the electron in the metal. comparing this equation with the experimental equation Ek = A v — B, it becomes clear that A is actually Planck's constant h and B is the work-function W of the metal. If the energy of the photon absorbed by the electron is less than the work-function W of the metal, then the electron will not be emitted. Therefore, if for the given metal, the threshold frequency of light be vo, then minimum amount of energy hvo of the photon of light will be spent in ejecting the electron out of the metal, that is, it will be equal to the work-function W. Thus,
W=h vo
Substituting this value of W in the last equation, we get
Ek = hv — hvo
Ek = h(v — vo)
If the maximum velocity of the emitted photoelectrons be vmax , then Ek=1/2 mvmax2 Hence, the above equation may also be written as
This equation is called 'Einstein's photoelectric equation'. The laws of photoelectric effect can be explained by this equation.
1
/
2
mvmax2=h(v-vo)
and explain the laws of photoelectric effect on its basis.
solutions
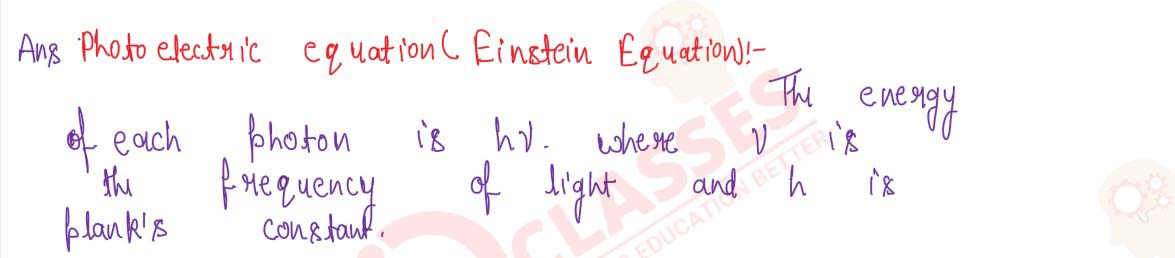suppose, the (maximum) kinetic energy of photoelectrons emitted from the metal-surface is
Ek and W is
the energy required to eject a photoelectron from the metal. W is the work-function of the metal.
Then,
according to the above explanation, we have
hv=W+Ek
Ek=hv-W
where h v is the energy of the photon absorbed by the electron in the metal. comparing this equation with the experimental equation Ek = A v — B, it becomes clear that A is actually Planck's constant h and B is the work-function W of the metal. If the energy of the photon absorbed by the electron is less than the work-function W of the metal, then the electron will not be emitted. Therefore, if for the given metal, the threshold frequency of light be vo, then minimum amount of energy hvo of the photon of light will be spent in ejecting the electron out of the metal, that is, it will be equal to the work-function W. Thus,
W=h vo
Substituting this value of W in the last equation, we get
Ek = hv — hvo
Ek = h(v — vo)
If the maximum velocity of the emitted photoelectrons be vmax , then Ek=1/2 mvmax2 Hence, the above equation may also be written as
1
/
2
mvmax2=h(v-vo)=hc(
1
/
λ
-
1
/
λo
)
This equation is called 'Einstein's photoelectric equation'. The laws of photoelectric effect can be explained by this equation.
Q5
Plot a labelled graph of(Vo),
where Vo
is the stopping potential of photoelectrons versus frequency V of incident radiation. How will you
use this graph to determine the value of Planck's constant? Explain.
solutions
Vo= (
This is the equation Of the Vo versus v graph. It represents a straight line since h and e are constants and vo is constant for a given surface. Now, according to Eq. (iii), the slope of the straight-line graph is h/e. Thus,
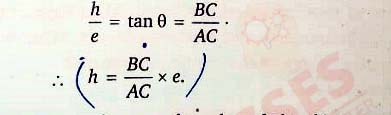
Hence, using the known value of electronic charge e, the value of Planck's constants can be obtained.
solutions
Vo= (
h
/
e
)v- (
h
/
e
)vo
This is the equation Of the Vo versus v graph. It represents a straight line since h and e are constants and vo is constant for a given surface. Now, according to Eq. (iii), the slope of the straight-line graph is h/e. Thus,
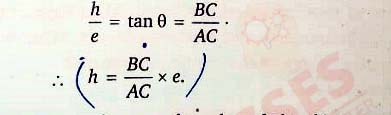
Hence, using the known value of electronic charge e, the value of Planck's constants can be obtained.