Long Answer Type [A]
1
What is ‘current density’? Write the vector equation
connecting current density j⃗ with electric field
intensity E⃗, for an ohmic conductor.
Solution




2
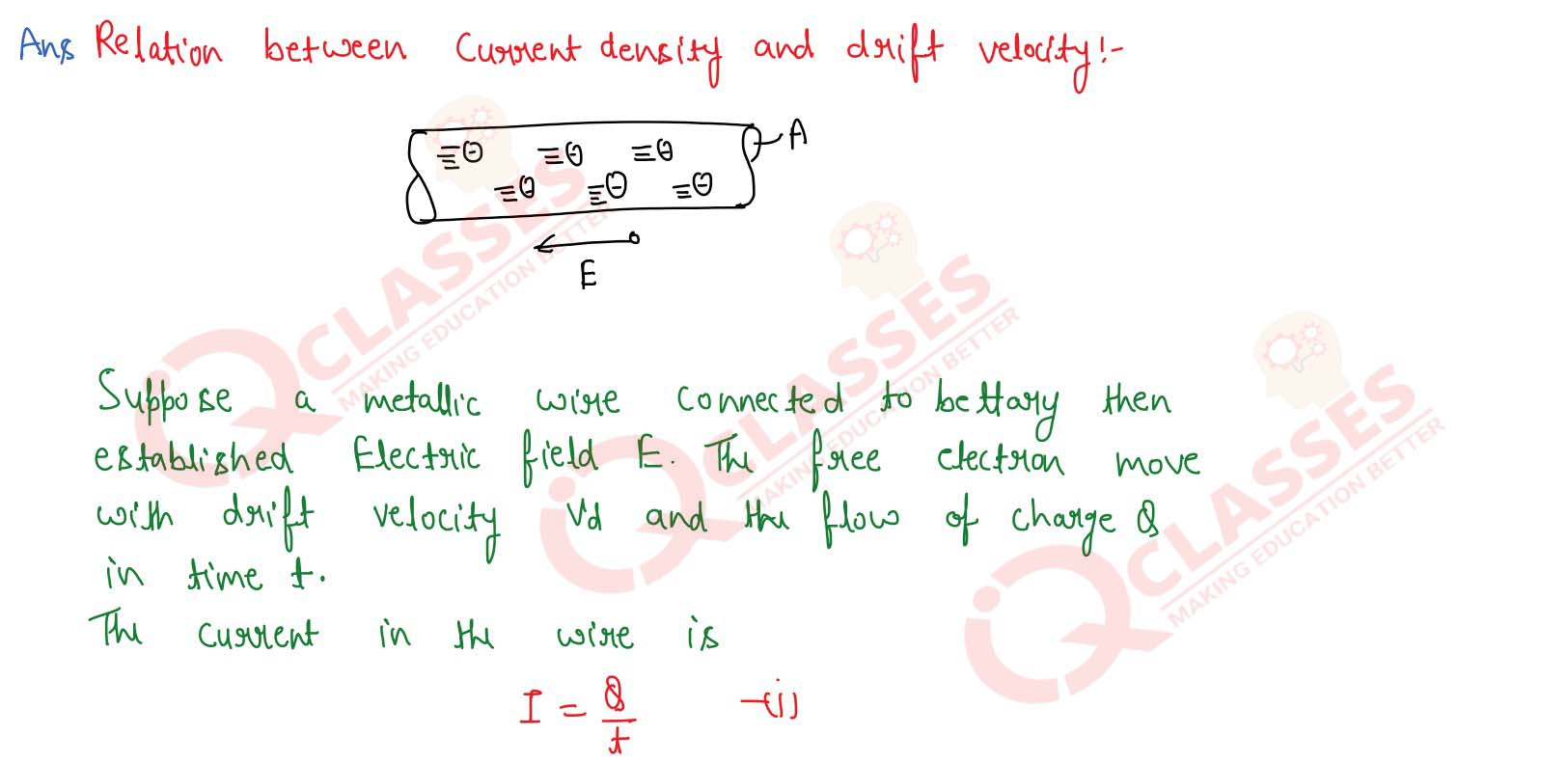
Obtain an expression showing the relation between
the current-density j in a current-carrying conductor, the drift velocity vd, the number of
free electrons per
unit volume n and the electronic charge e.
Solution





3
The current flowing through a conductor is given by
T = neAvd.
(i) Identify each term in the equation.
(ii) Obtain an expression for vd , if the current flowing through the conductor of length l has its ends maintained at a potential difference of V volt. Solution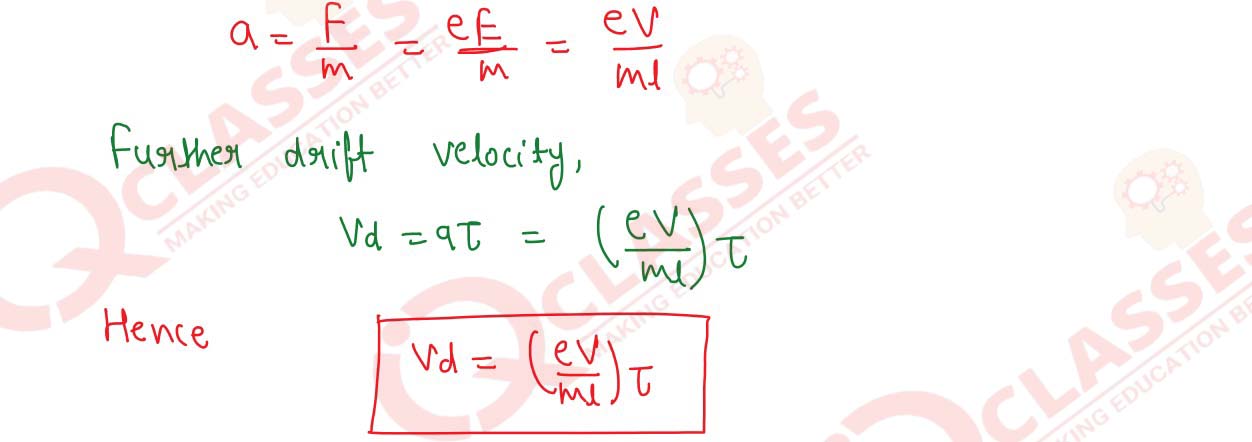
(i) Identify each term in the equation.
(ii) Obtain an expression for vd , if the current flowing through the conductor of length l has its ends maintained at a potential difference of V volt. Solution
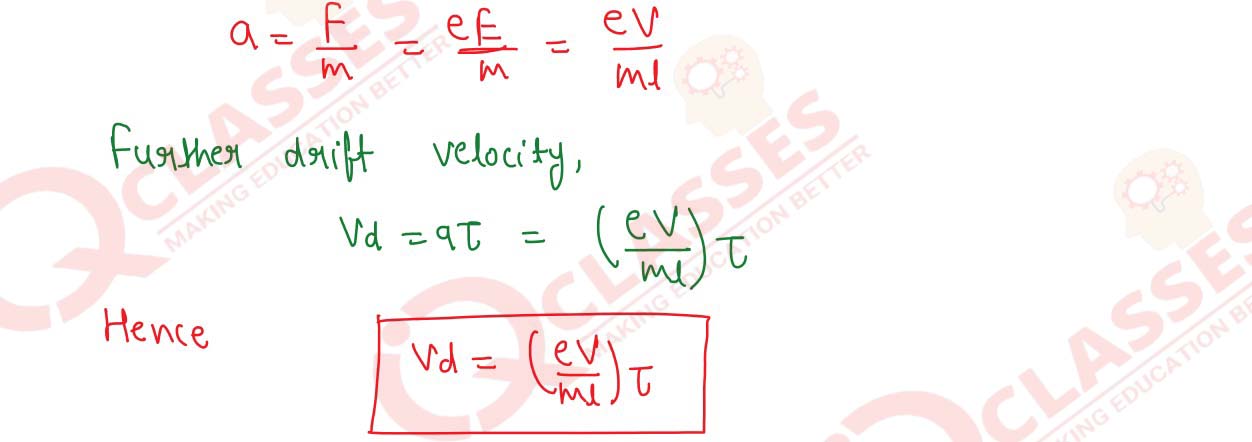

4
State Ohm’s law. Derive it on the basis of the concept
of drift velocity of free electrons in metals.
Solution








5
What is meant by specific resistance (resistivity) of
a conductor? Write its unit. Show how the electric
resistance of a wire depends on the resistivity of its
material, its length and area of cross-section
Solution






6
Ohm's law may also be stated by the equation j⃗ = σ E⃗,
What do the symbols j⃗,σ and E⃗ stand for? Show that a combination of units on the two
sides are
identical.
Solution

Solution


7
Define resistivity of a conductor explain the variation of resistance with temperature in
(i) metallic wire
(ii) a piece of carbon
Solution

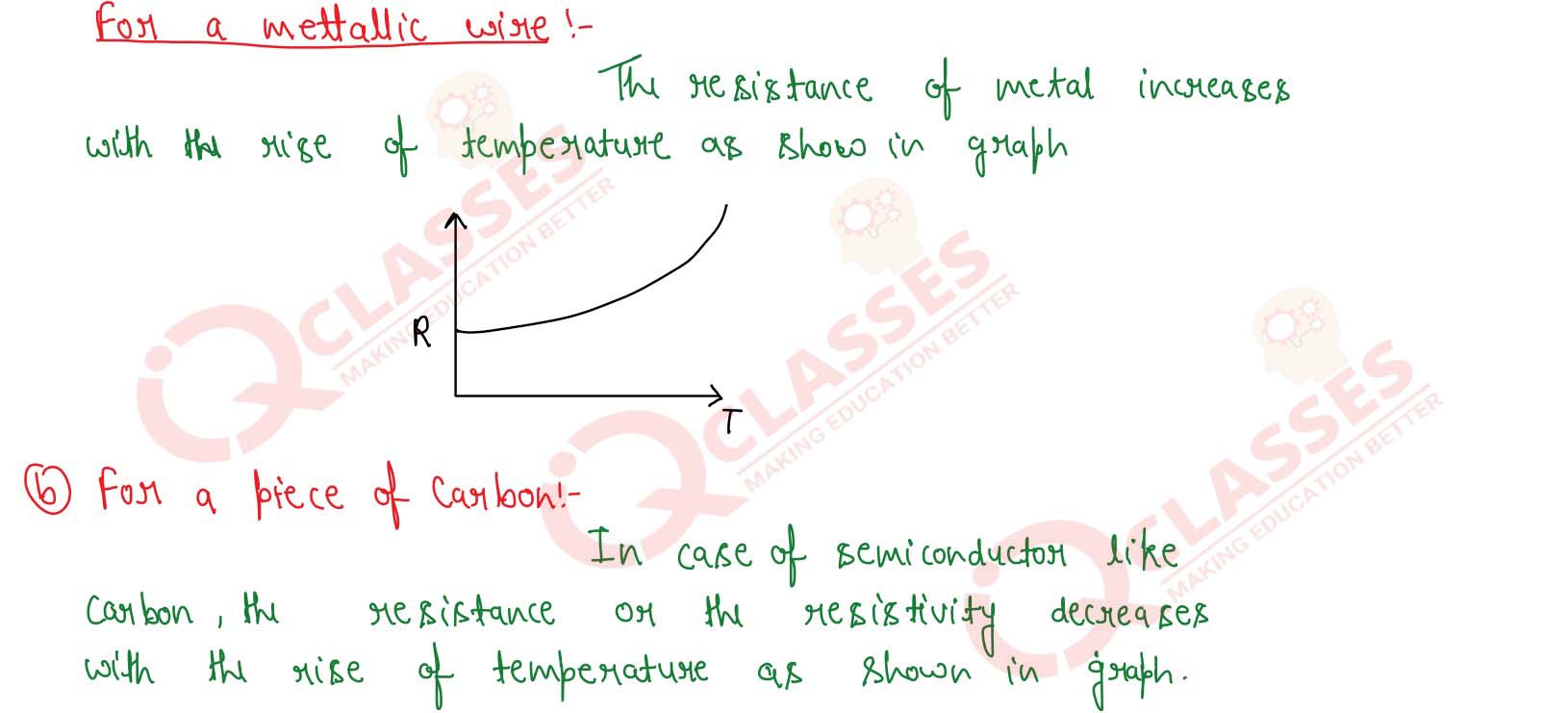
(i) metallic wire
(ii) a piece of carbon
Solution



8
Write down a simple relationship to show the variation of resistance in temperature define temperature
coefficient of resistance in what way the temperature coefficient of carbon is different from that of
carbon conductors
Solution


9
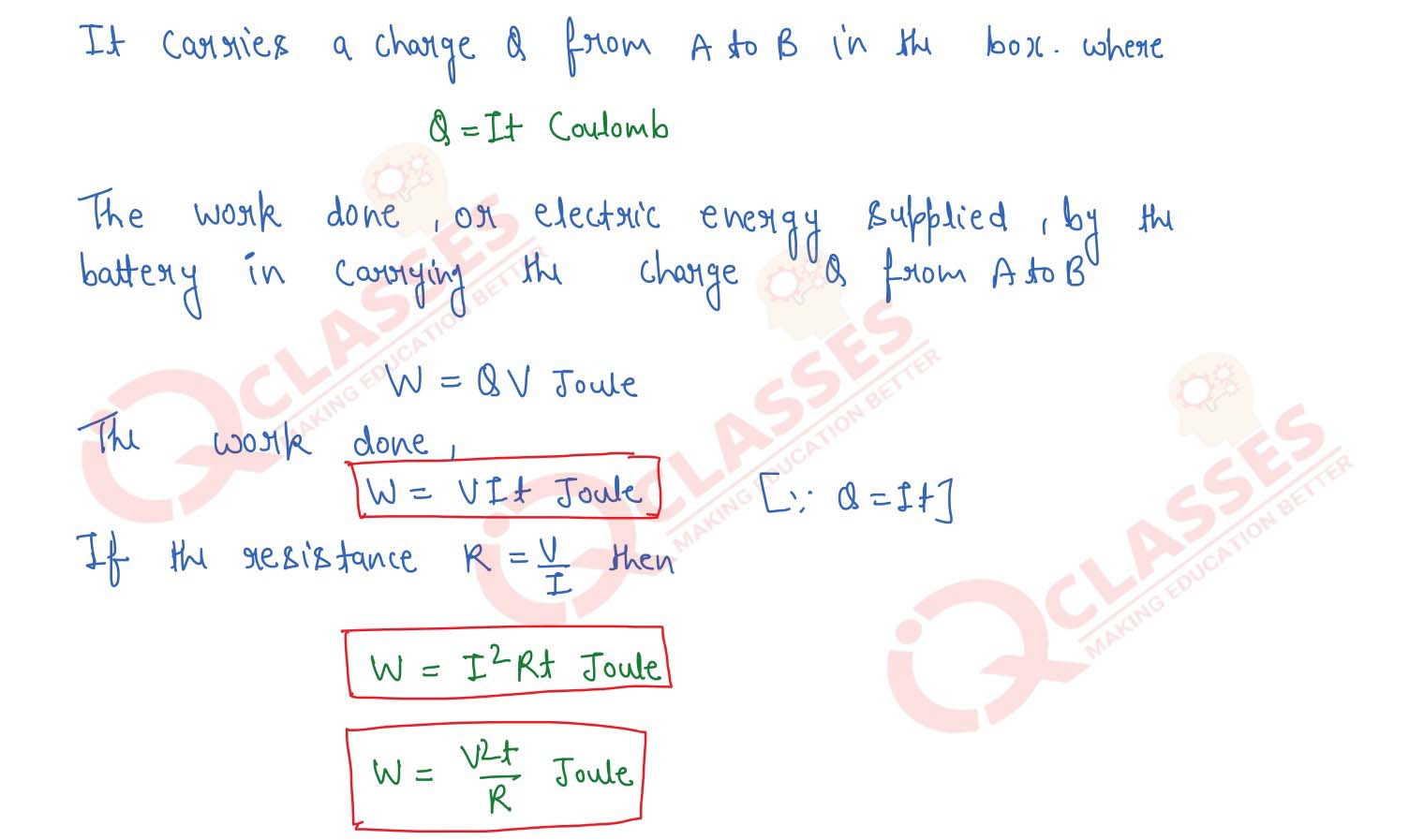
Explain energy transfer in electric circuits prove that the energy liberated from an electric circuit is
given by W = VIt = I2Rt = V2t/R where symbols have usual meanings
Solution





10
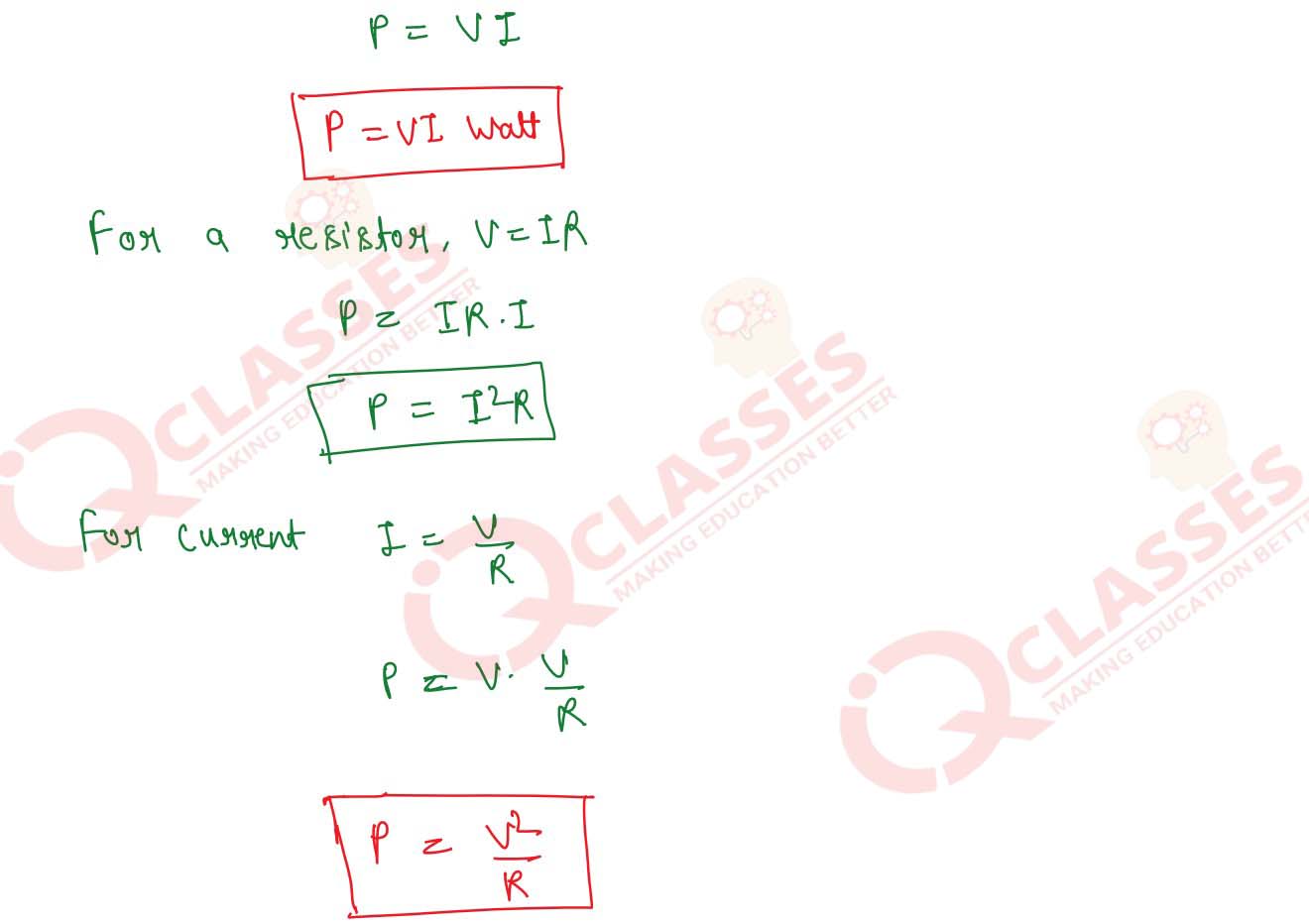
What do you mean by electric power? Obtain various
expressions for electric power in a circuit.
Solution





11
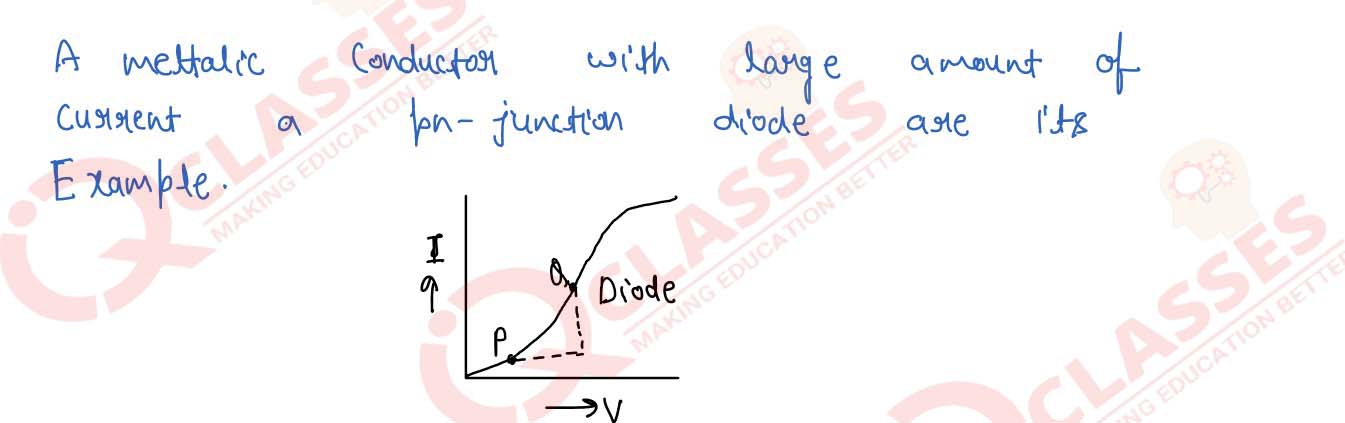
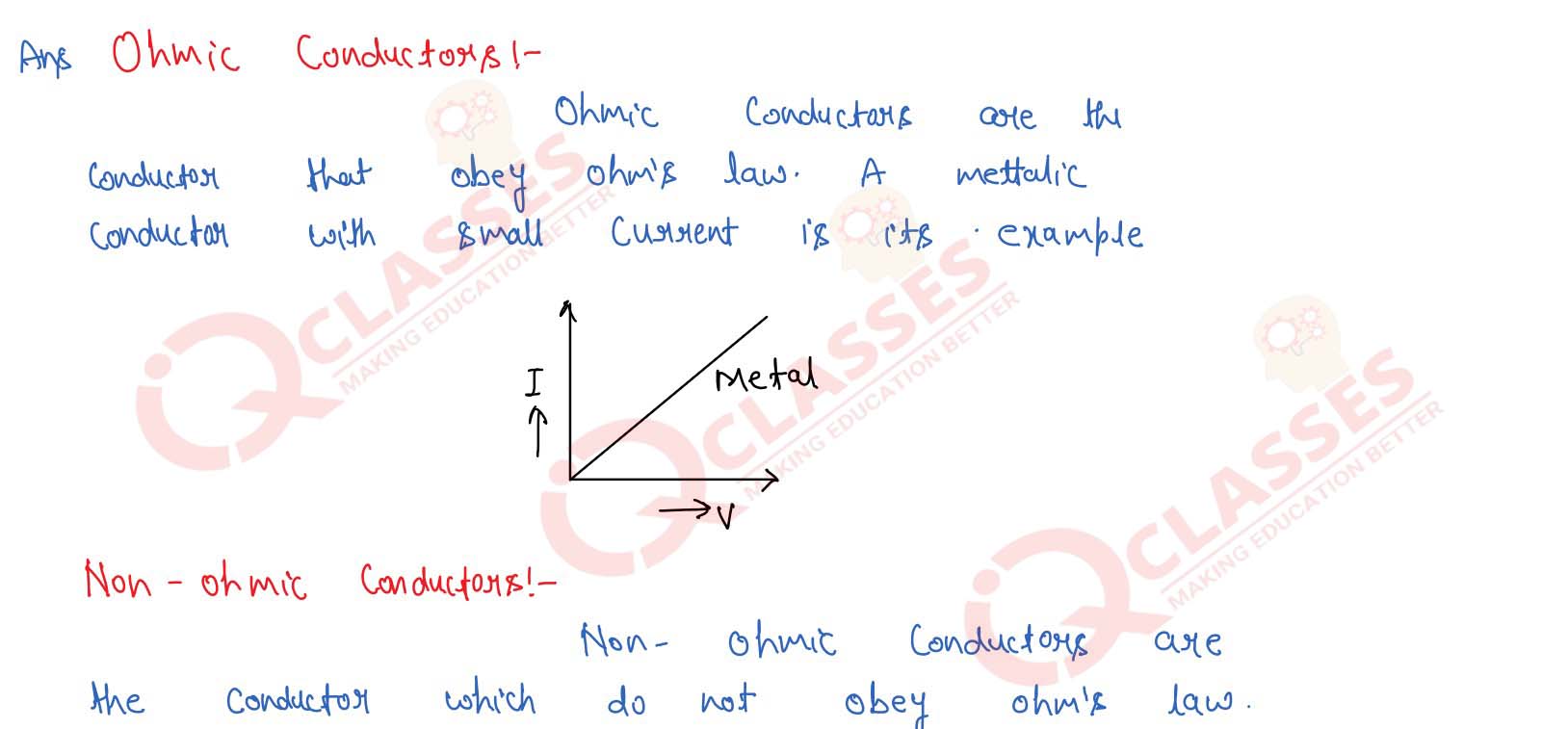
What are ohmic and non ohmic conductors explain give an example of each and draw their V-I
characteristics.
Solution



12
Show that the equivalent resistance of a series combination is always greater than any one of the
individual resistances
Solution



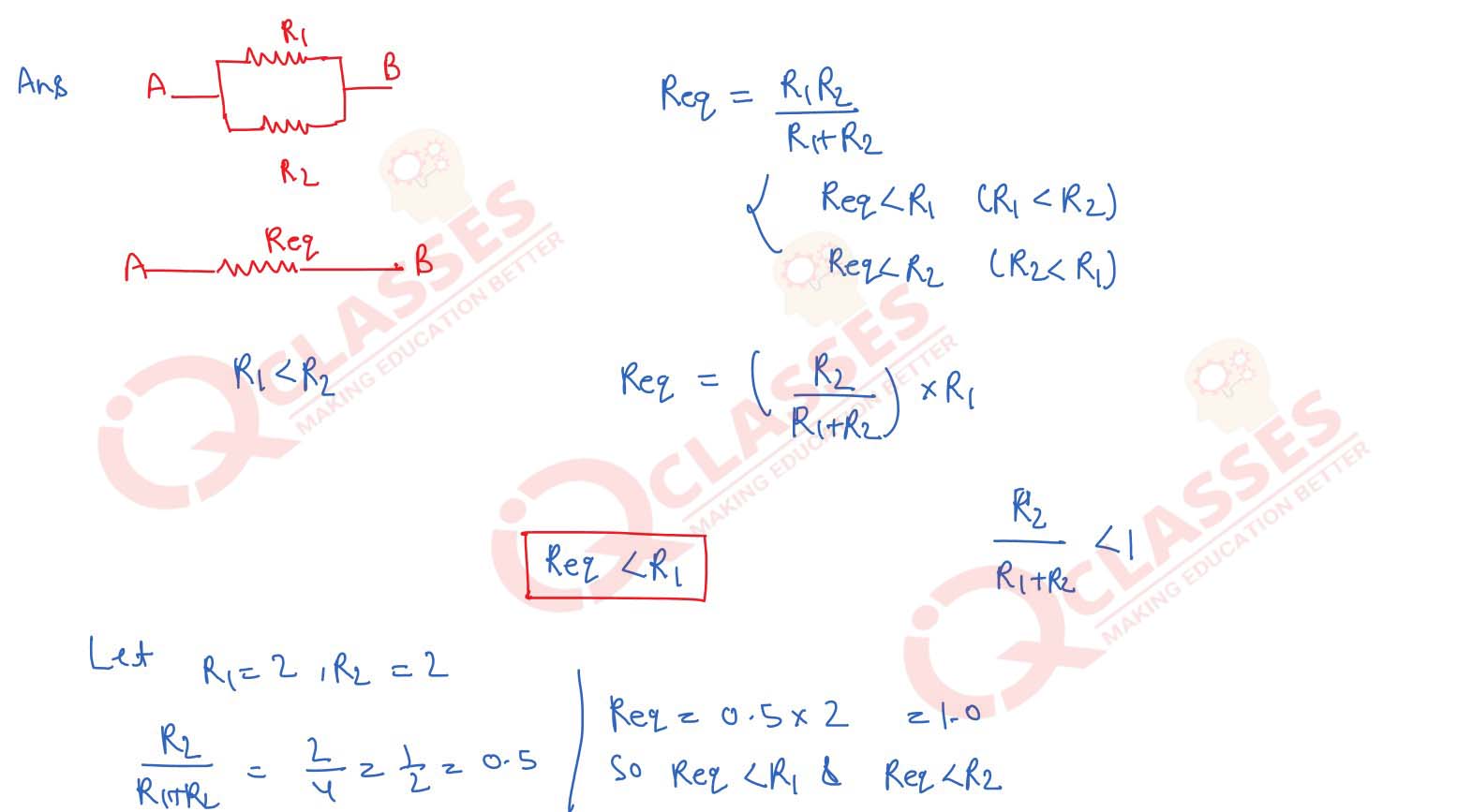
13
Show that the equivalent resistance of a parallel combination is less than any one of the resistances

