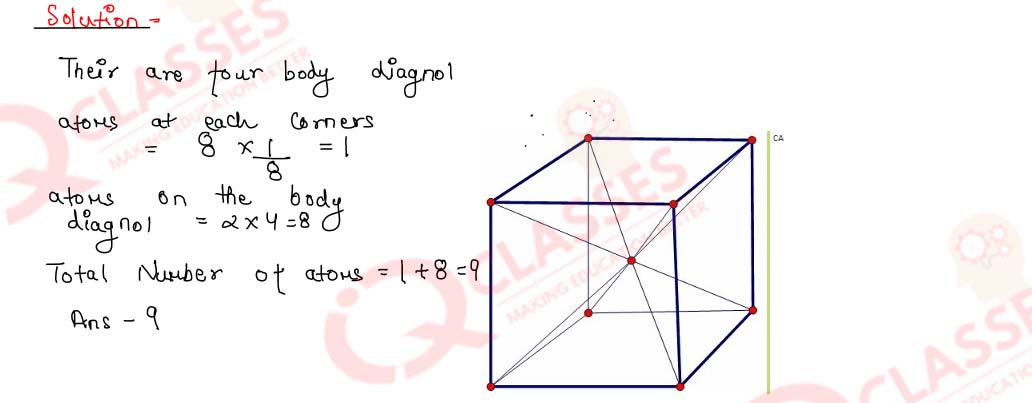
1.1) Calculate the number of atoms in a cubic based unit cell having one atom at each corner and two atoms on each diagonal.
Solution
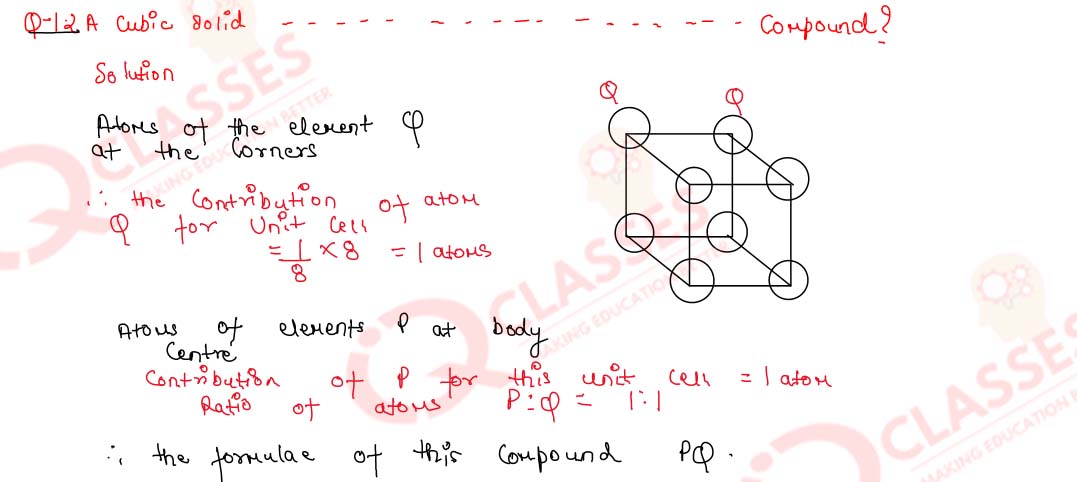
1.2) A cubic solid is made up of two elements P and Q. Atoms Q are present at the corner of the cube and atom P at the body centre. What is the formula of the compound?
Solution
1.3)
The density of KBr is 2.75 g cm-3. The length of the edge of the unit cell is 654 pm.
Show that KBr has a face-centred cubic structure.
(NA= 6.023x1023 mol-1, Atomic masses : K= 39, Br = 80)
Solution

1.4)
A body-centred cubic element of density 10.3 g cm-3 has a cell edge of 3.14 pm, Calculate
the atomic
mass of the element.
(Avogadro's constant, NA= 6.023 x 1023 mol-1).
Solution

1.5) An element of atomic mass 98.5 g mol- occurs in fcc structure. If its unit cell edge length is 500 pm and its density is 5.22 g cm-3, what is the value of Avogadro's constant?
Solution

1.6)
The compound CuCl has ZnS structure and the edge length of its unit cell is 500 pm. Calculate its
density.
(Atomic masses : Cu = 63, C1 = 35.5; Avogadro's const. = 6.02x1023mol-1)
Solution

1.7)
A metal has a foc structure. The length of its unit cell is 404 pm. What is the molar mass of metal,
if the density of the metal is 2.72 g cm-3?
(NA= 6.023 x1023 atoms mol-1).
Solution

1.8) KF has NaCl structure. What is the distance between K+ and F- in KF, if the density of KF is 2.48 g cm-3 ?
Solution

1.9)
Given for iron, a = 288 pm, p = 7.86 g cm-3 . Find the type of cubic lattice to which the
crystal belongs. Also calculate the radius of iron atom.
(Atomic mass of Fe = 55.85)
Solution

1.10)
An element A (atomic mass 100) having bcc structure has unit cell edge of 400 pm. Calculate the
density of A and the number of unit cells for 10 g of A.
(NA = 6.023 x 1023).
Solution

1.11)
Chromium has monoatomic body-centred cubic structure. Its cell edge is 300 pm. What is its density?
(Molar mass of Cr = 52 g mol-1, NA = 6.023x1023 mol-1).
Solution

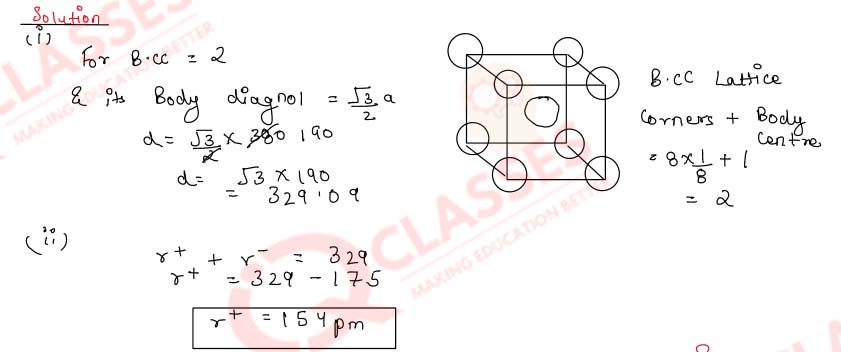
1.12) A compound AB crystallises in the bcc lattice with unit cell edge length of 380 pm. Calculate
- the distance between the oppositely charged ions in the lattice;
- radius of A* if radius of B-is 175 pm.
Solution
1.13)
An element crystallises in body-centred cubic lattice. It has a density of 10 g cm-3 at
room
temperature. Calculate the atomic radius of the element.
(Atomic mass = 60.23)
Solution

1.14)
Lithium metal crystal has a body-centred cubic structure. Its density is 0.53 g cm-3 and
its molar
mass is 6.94 g mol-1. Calculate the volume of a unit cell of lithium metal
(NA = 6.023 x 1023 mol-1).
Solution

1.15)
Determine the type of cubic lattice to which the crystal of the element indicated hereafter belongs.
It has an edge length of 290 pm and a density of 7.80 g cm-3.
(At. mass of element = 56.0 amu)
Solution

1.16)
Caesium chloride crystallises as a body-centred cubic lattice and has a density of 4.0 g
cm-3.
Calculate the length of the edge of the unit cell of caesium chloride crystal.
(Molar mass of CsCl = 168.5 g mol-1, NA = 6.02 x 102 mol-1)
Solution

1.17)
Calculate the density of silver which crystallises in the face centred cubic structure. The distance
between the nearest silver atoms in this structure is 287 pm.
(Molar mass of Ag = 107.87 g mol-1, NA = 6.02x1023
mol-1)
Solution

1.18) Define the term 'amorphous'.
Solution
In amorphous solid ,the structural unit are not arranged in a definite pattern
->they have short range order
->amorphous solid are generally regarded as super cooled liquid
Example-Glass,rubber,plastic etc
1.19)
Calculate the value of Avogadro constant from the following data :
Density of NaCl = 2.165 g cm-3
Distance between Na+ and Cl- in NaCl = 281pm
(Molar mass of NaCl = 58.5 g mol-1)
Solution

1.20) Aluminium metal forms a cubic close-packed structure. Its atomic radius is 1.25x10-12 m.
- Calculate the length of the side of the unit cell.
- How many such unit cells are there in 100 m3 of aluminium?
Solution

1.21) How many atoms can be assigned to its unit cell if an element forms
- a body-centred-cubic unit cell, and
- a face-centered cubic cell ?