Q1
By using standard formulae, expand the following (1 to 9):
(i) (2x + 7y)2
(ii) (1/2 x + 2/3 y)2
solutions
(i) (2x + 7y)2
(ii) (1/2 x + 2/3 y)2
solutions

Q2
(i) (3x + 1/2x)2
(ii) (3x2 y + 5z)2
solutions
(ii) (3x2 y + 5z)2
solutions

Q3
(i) (3x – 1/2x)2
(ii) (1/2 x – 3/2 y)2
solutions
(ii) (1/2 x – 3/2 y)2
solutions

Q4
. (i) (x + 3) (x + 5)
(ii) (x + 3) (x – 5)
(iii) (x – 7) (x + 9)
(iv) (x – 2y) (x – 3y)
solutions
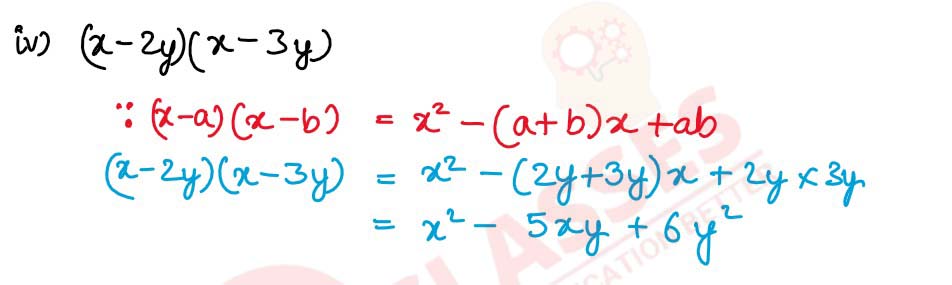
(ii) (x + 3) (x – 5)
(iii) (x – 7) (x + 9)
(iv) (x – 2y) (x – 3y)
solutions

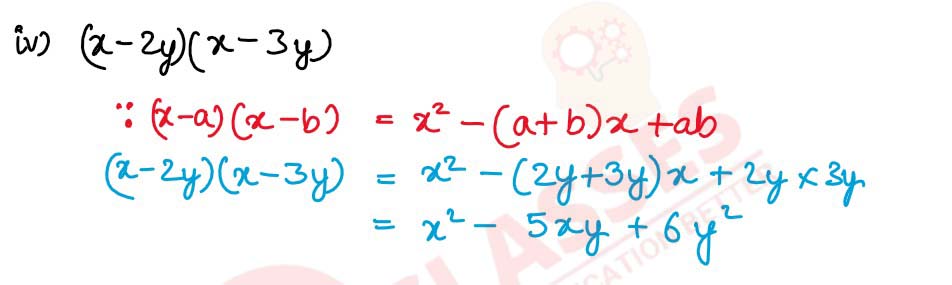
Q5
(i) (x – 2y – z)2
(ii) (2x – 3y + 4z)2
solutions
(ii) (2x – 3y + 4z)2
solutions

Q6
(i) (2x + 3/x – 1)2
(ii) (2/3 x – 3/2x – 1)2
solutions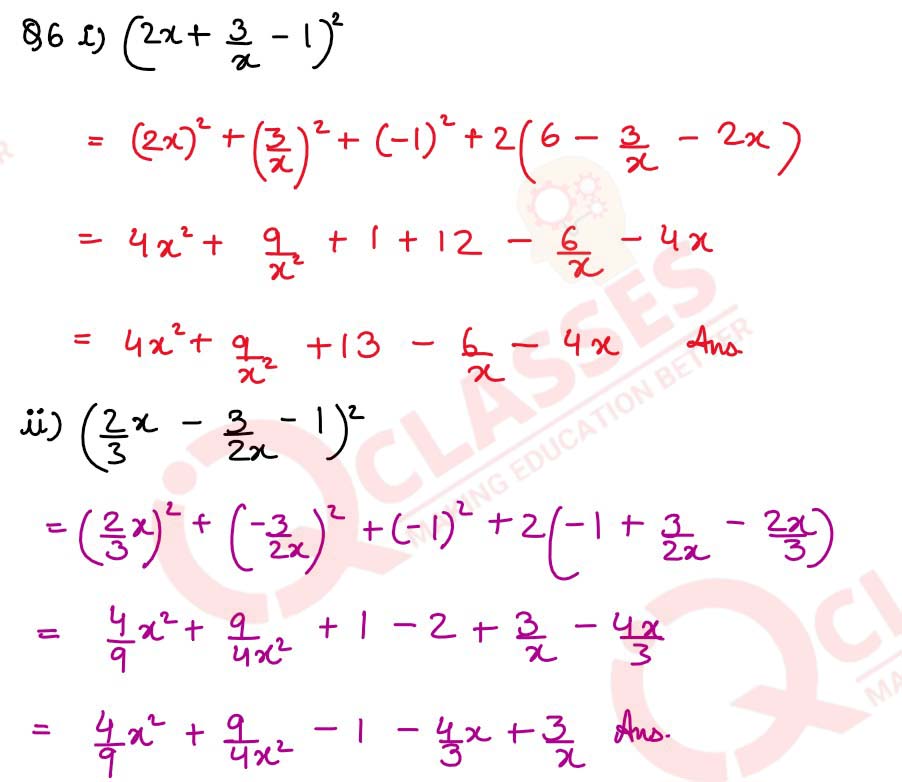
(ii) (2/3 x – 3/2x – 1)2
solutions
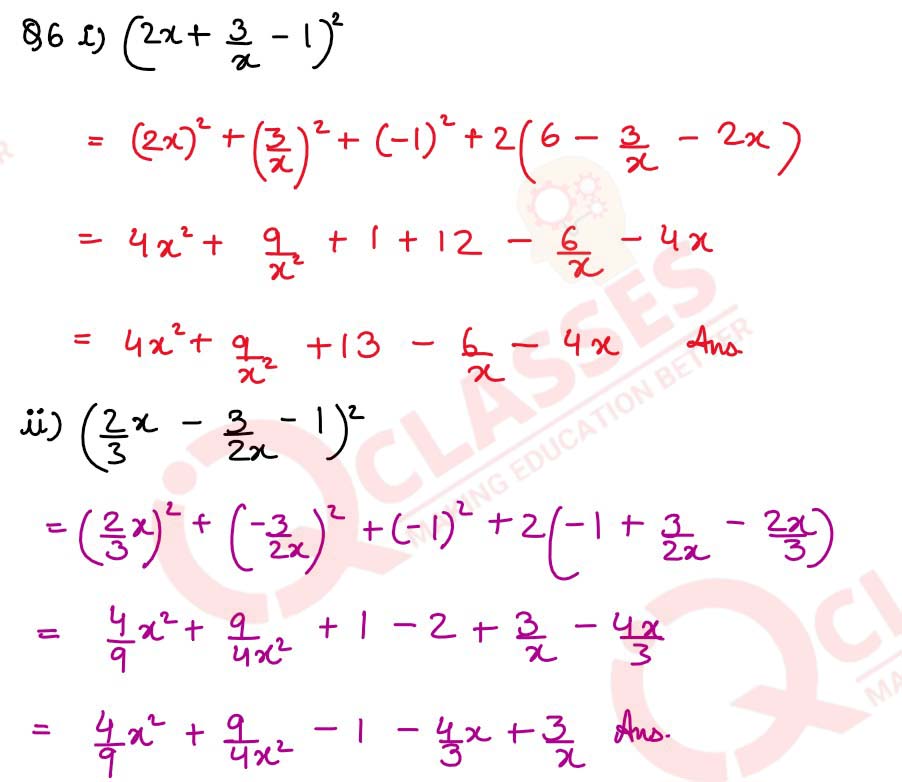
Q7
(i) (x + 2)3
(ii) (2a + b)3
solutions
(ii) (2a + b)3
solutions

Q8
A man has certain notes of denominations Rs. 20 and Rs. 5 which amount to Rs. 380. If the number of notes of each kind is interchanged, they amount to Rs. 60 less as before. Find the number of notes of each denomination.
solutions
solutions

Q9
(i) (3x + 1/x)3
(ii) (2x – 1)3
solutions
(ii) (2x – 1)3
solutions

Q10
Simplify the following (10 to 19):
(i) (a + b)2 + (a – b)2
(ii) (a + b)2 – (a – b)2
solutions
(i) (a + b)2 + (a – b)2
(ii) (a + b)2 – (a – b)2
solutions

Q11
(i) (a + 1/a)2 + (a – 1/a)2
(ii) (a + 1/a)2 – (a – 1/a)2
solutions
(ii) (a + 1/a)2 – (a – 1/a)2
solutions

Q12
(i) (3x – 1)2
– (3x – 2) (3x + 1)
(ii) (4x + 3y)2 – (4x – 3y)2 – 48xy
solutions
(ii) (4x + 3y)2 – (4x – 3y)2 – 48xy
solutions

Q13
(i) (7p + 9q) (7p – 9q)
(ii) (2x – 3/x) (2x + 3/x)
solutions
(ii) (2x – 3/x) (2x + 3/x)
solutions

Q14
(i) (2x – y + 3) (2x – y – 3)
(ii) (3x + y – 5) (3x – y – 5)
solutions
(ii) (3x + y – 5) (3x – y – 5)
solutions

Q15
(i) (x + 2/x – 3) (x – 2/x – 3)
(ii) (5 – 2x) (5 + 2x) (25 + 4x2 )
solutions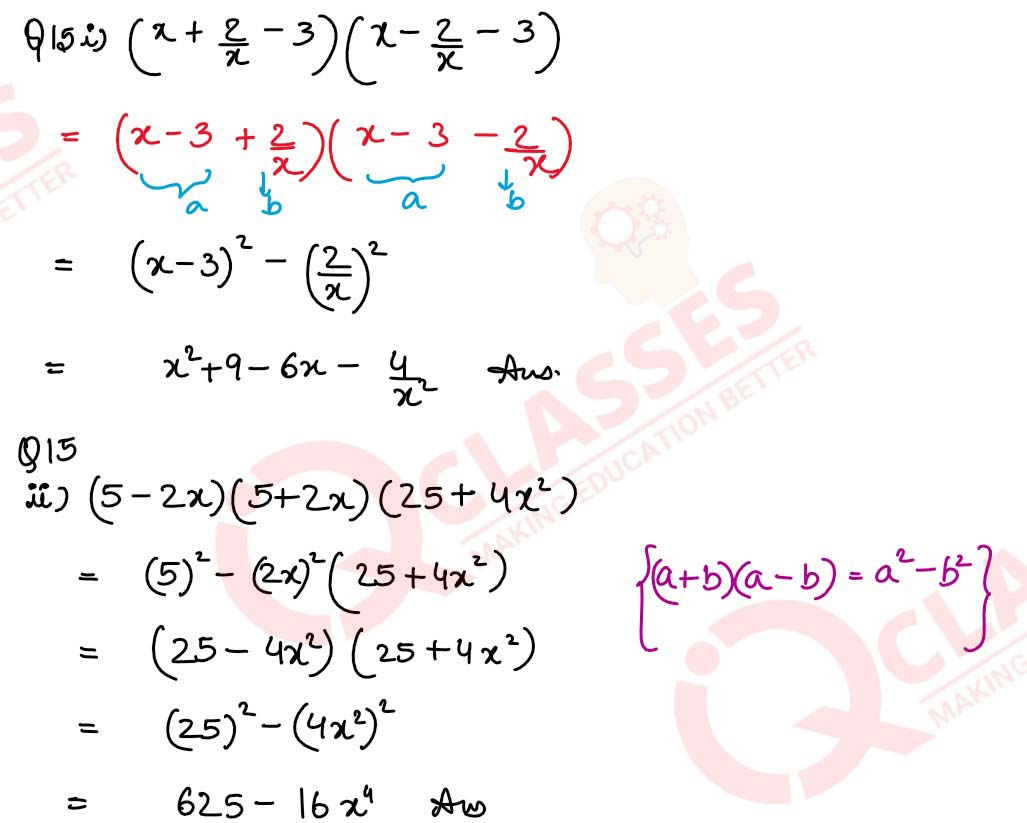
(ii) (5 – 2x) (5 + 2x) (25 + 4x2 )
solutions
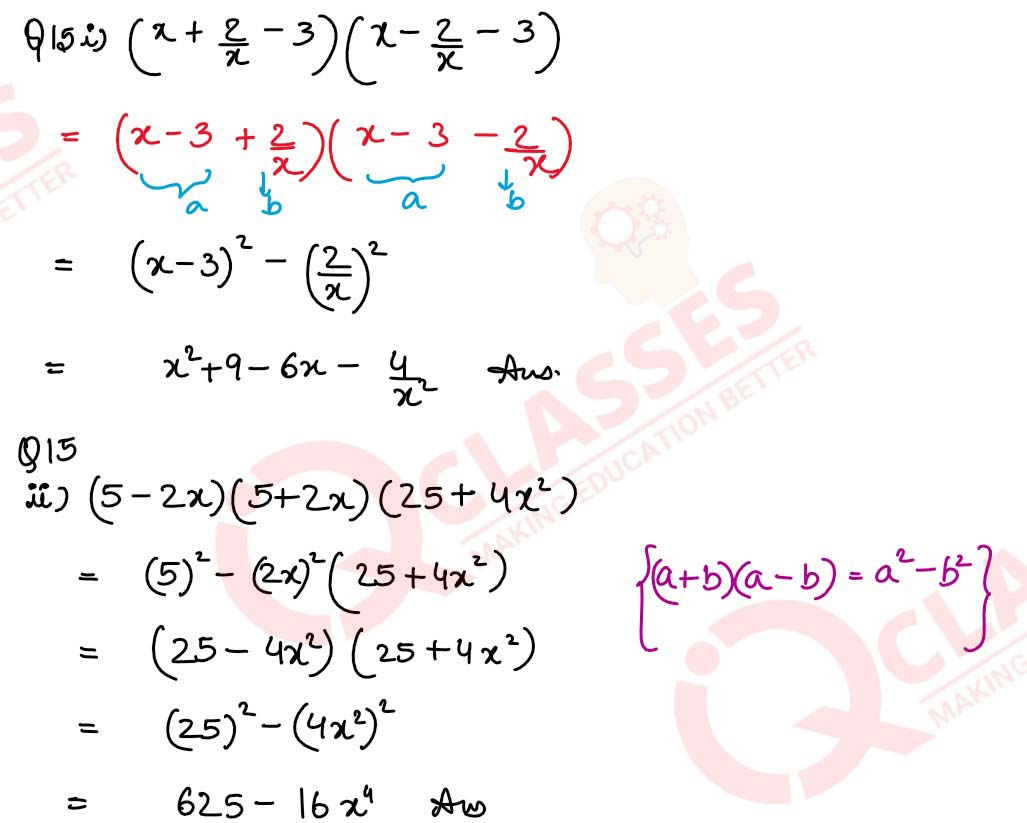
Q16
(i) (x + 2y + 3) (x + 2y + 7)
(ii) (2x + y + 5) (2x + y – 9)
(iii) (x – 2y – 5) (x – 2y + 3)
(iv) (3x – 4y – 2) (3x – 4y – 6)
solutions

(ii) (2x + y + 5) (2x + y – 9)
(iii) (x – 2y – 5) (x – 2y + 3)
(iv) (3x – 4y – 2) (3x – 4y – 6)
solutions


Q17
(i) (2p + 3q) (4p2
– 6pq + 9q2
)
(ii) (x + 1/x) (x2 - 1 + 1/x2 )
solutions
(ii) (x + 1/x) (x2 - 1 + 1/x2 )
solutions

Q18
(i) (3p – 4q) (9p2 + 12pq + 16q2
)
(ii) (x – 3/x) (x2 + 3 + 9/x2 )
solutions
(ii) (x – 3/x) (x2 + 3 + 9/x2 )
solutions

Q19
(2x + 3y + 4z) (4x2 + 9y2 + 16z2
– 6xy – 12yz – 8zx).
solutions
solutions

Q20
Find the product of the following:
(i) (x + 1) (x + 2) (x + 3)
(ii) (x – 2) (x – 3) (x + 4)
solutions
(i) (x + 1) (x + 2) (x + 3)
(ii) (x – 2) (x – 3) (x + 4)
solutions

Q21
Find the coefficient of x2
and x in the product of (x – 3) (x + 7) (x – 4).
solutions
solutions

Q22
If a2 + 4a + x = (a + 2)2
, find the value of x.
solutions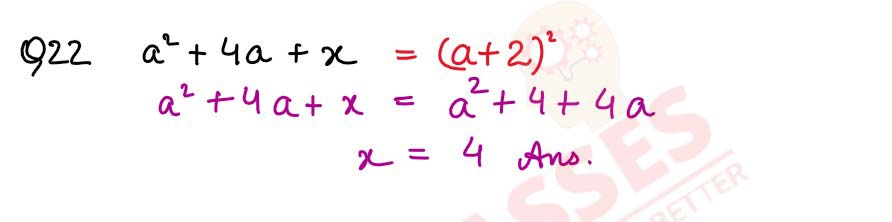
solutions
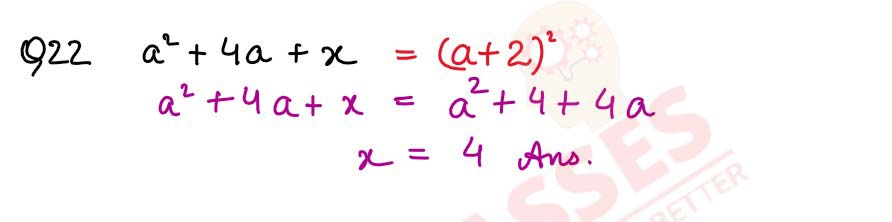
Q23
Use (a + b)2 = a2 + 2ab + b2
to evaluate the following:
(i) (101)2
(ii) (1003)2
(iii) (10.2)2
solutions
(i) (101)2
(ii) (1003)2
(iii) (10.2)2
solutions

Q24
Use (a – b)2 = a2
– 2ab – b
2
to evaluate the following:
(i) (99)2
(ii) (997)2
(iii) (9.8)2
solutions
(i) (99)2
(ii) (997)2
(iii) (9.8)2
solutions

Q25
By using suitable identities, evaluate the following:
(i) (103)3
(ii) (99)3
(iii) (10.1)3
solutions
(i) (103)3
(ii) (99)3
(iii) (10.1)3
solutions

Q26
If 2a – b + c = 0, prove that 4a2
– b
2 + c2 + 4ac = 0.
solutions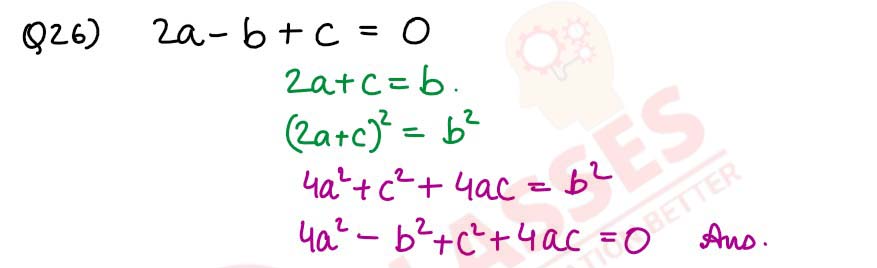
solutions
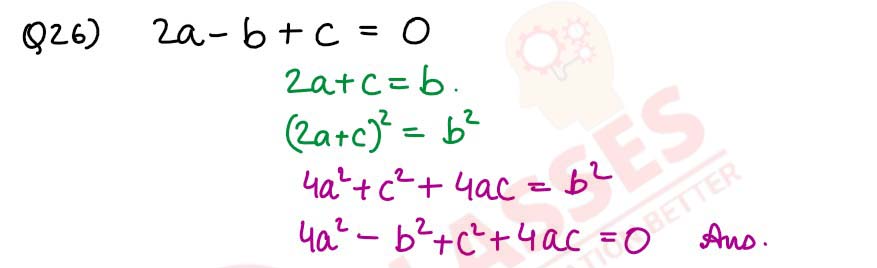
Q27
If a + b + 2c = 0, prove that a3 + b3 + 8c3 = 6abc.
solutions
solutions

Q28
If a + b + c = 0, then find the value of a2
/bc + b2
/ca + c2
/ab
solutions
solutions

Q29
If x + y = 4, then find the value of x3 + y3 + 12xy – 64.
solutions
solutions

Q30
Without actually calculating the cubes, find the values of:
(i) (27)3 + (-17)3 + (-10)3
(ii) (-28)3 + (15)3 + (13)3
solutions
(i) (27)3 + (-17)3 + (-10)3
(ii) (-28)3 + (15)3 + (13)3
solutions

Q31
Using suitable identity, find the value of:
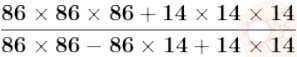
solutions
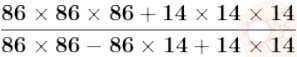
solutions
