Q1
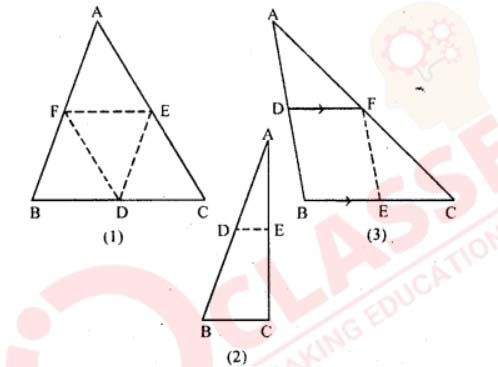
(a) In the figure (1) given below, D, E and F are mid-points of the sides BC, CA and AB respectively of ∆ ABC. If AB = 6 cm, BC = 4.8 cm and CA= 5.6 cm, find the perimeter of (i) the trapezium FBCE (ii) the triangle DEF.
(b) In the figure (2) given below, D and E are mid-points of the sides AB and AC respectively. If BC = 5.6 cm and∠B = 72°, compute (i) DE (ii)∠ADE.
(c) In the figure (3) given below, D and E are mid-points of AB, BC respectively and DF || BC. Prove that DBEF is a parallelogram. Calculate AC if AF = 2.6 cm.
solutions

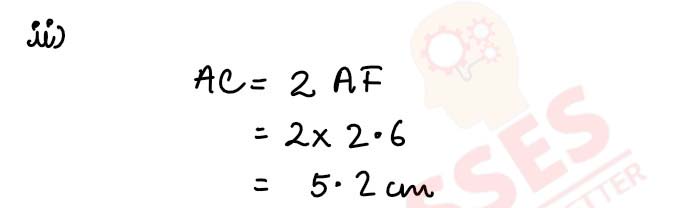
(b) In the figure (2) given below, D and E are mid-points of the sides AB and AC respectively. If BC = 5.6 cm and∠B = 72°, compute (i) DE (ii)∠ADE.
(c) In the figure (3) given below, D and E are mid-points of AB, BC respectively and DF || BC. Prove that DBEF is a parallelogram. Calculate AC if AF = 2.6 cm.

solutions


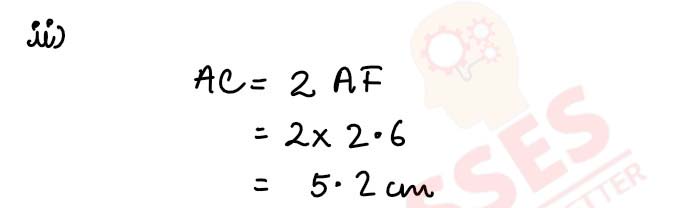
Q2
Prove that the four triangles formed by joining in pairs the mid-points of the sides c of a triangle are congruent to each other.
solutions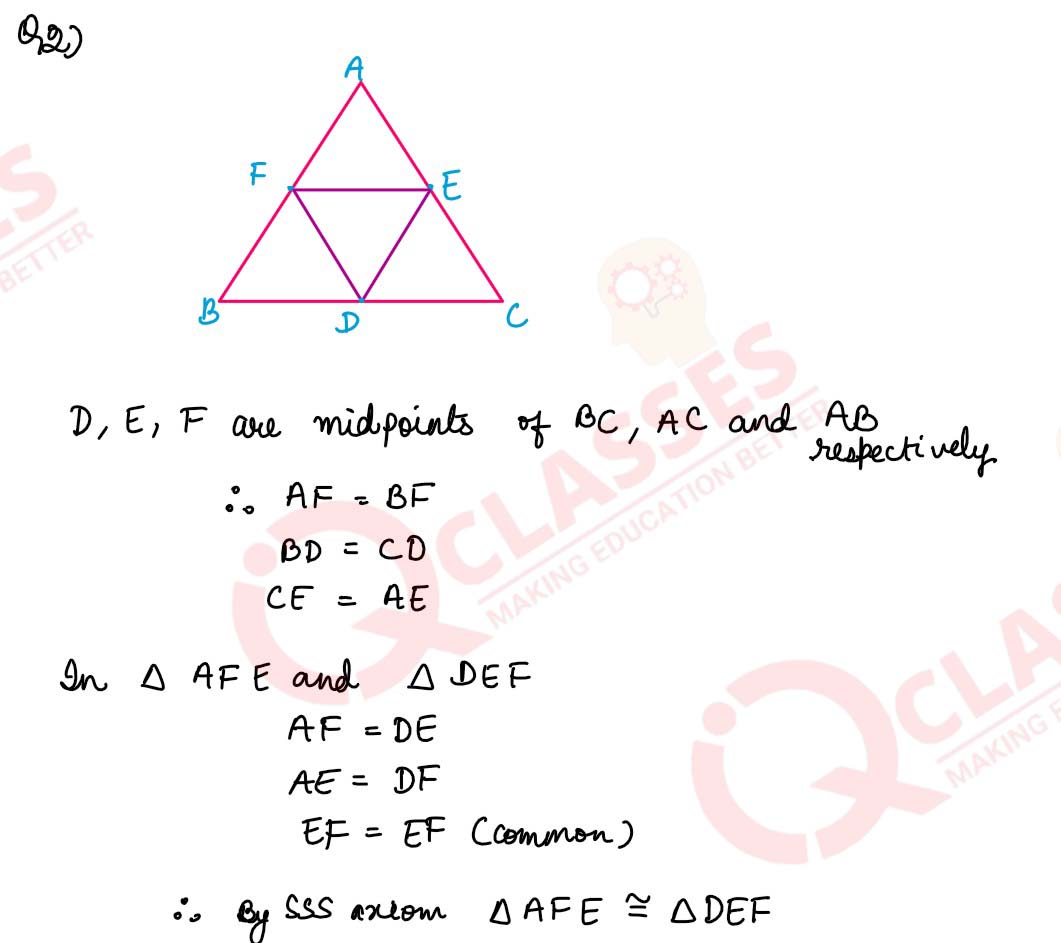
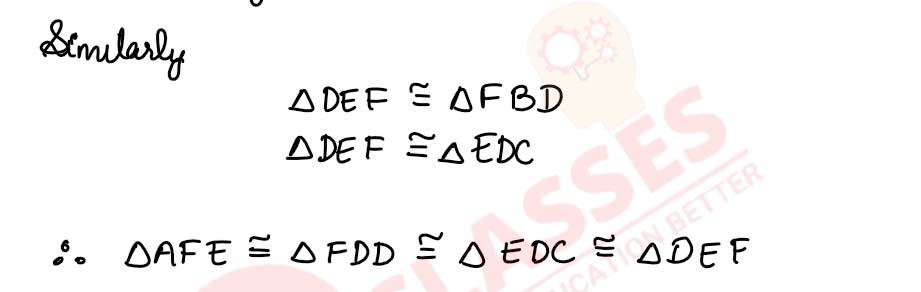
solutions

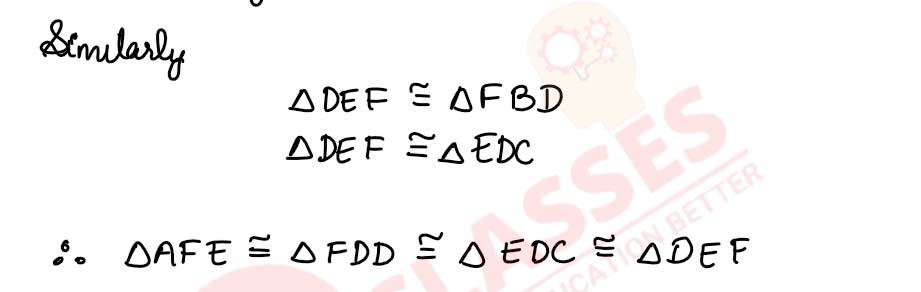
Q3
If D, E and F are mid-points of sides AB, BC and CA respectively of an isosceles triangle ABC, prove that ∆DEF is also F, isosceles
solutions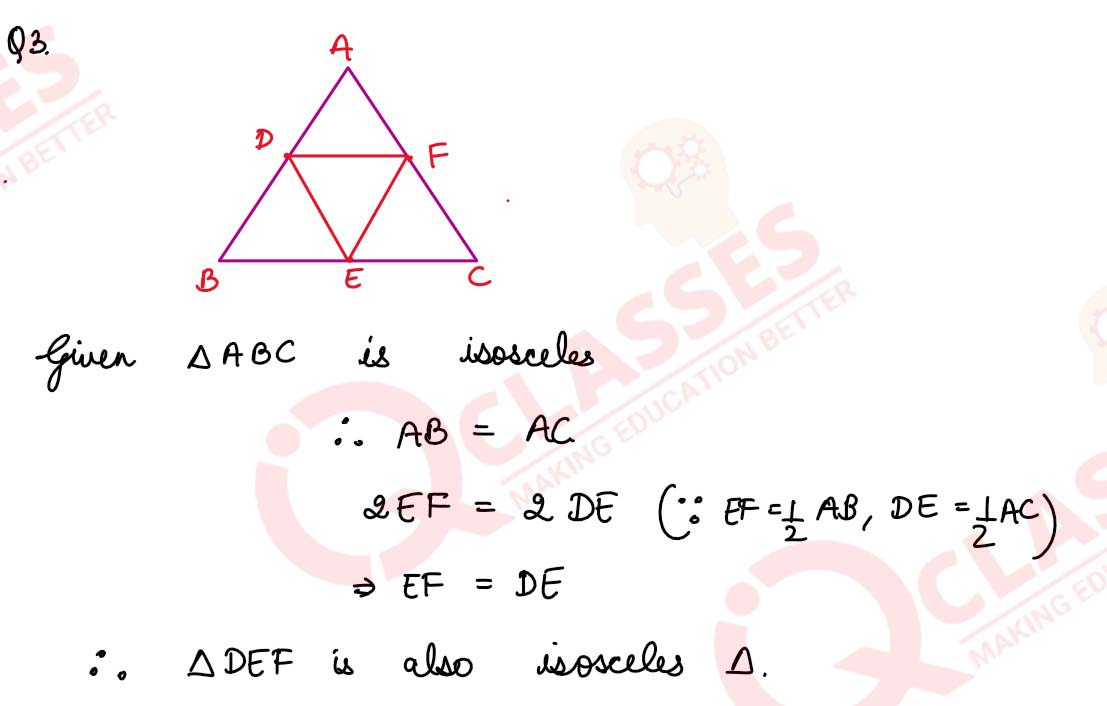
solutions

Q4
The diagonals AC and BD of a parallelogram ABCD intersect at O. If P is the mid-point of AD, prove that
(i) PQ || AB
(ii) PO=1/2CD.
solutions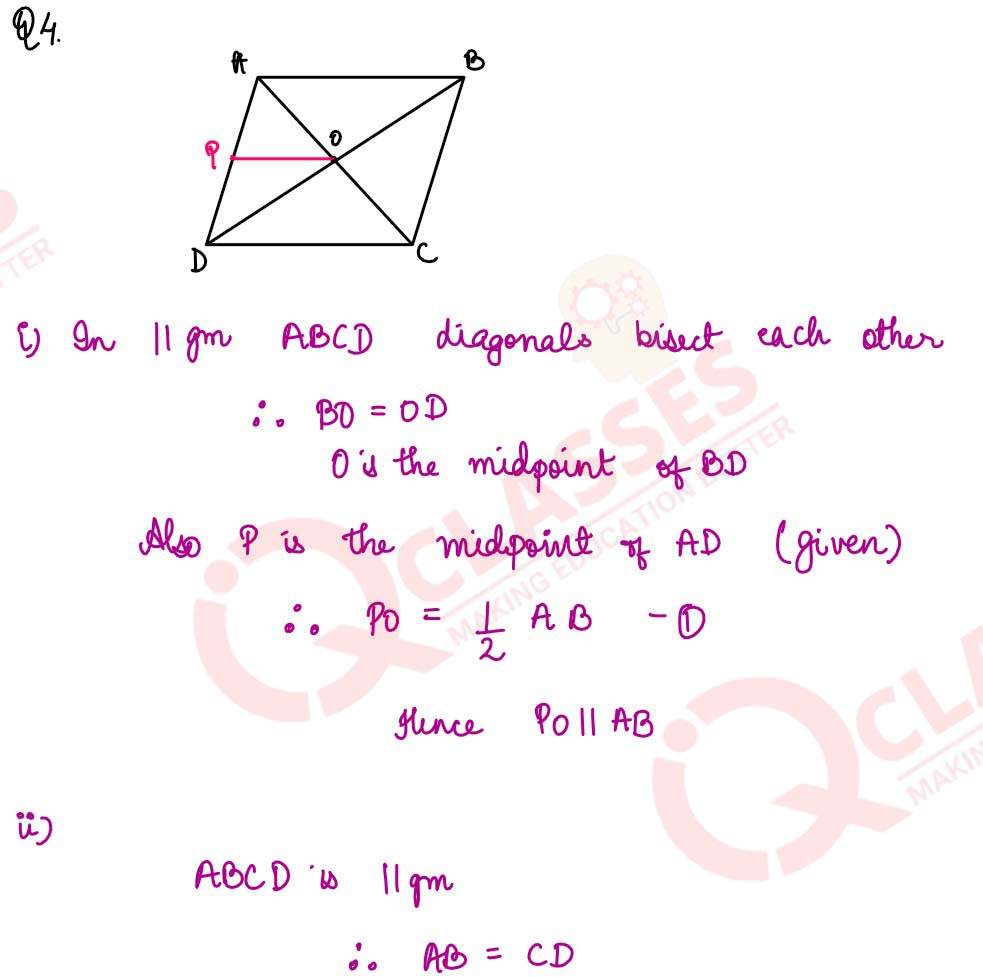
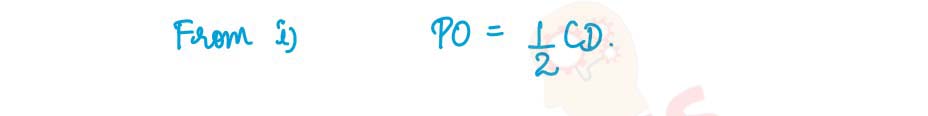
(i) PQ || AB
(ii) PO=1/2CD.
solutions

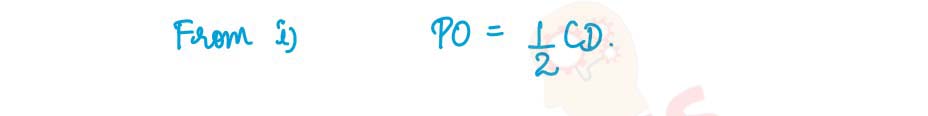
Q5
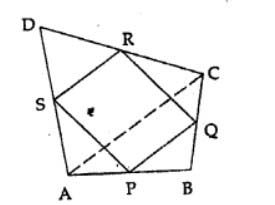
In the adjoining figure, ABCD is a quadrilateral in which P, Q, R and S are mid-points of AB, BC, CD and DA respectively. AC is its diagonal. Show that
(i) SR || AC and SR =1/2AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
solutions
(i) SR || AC and SR =1/2AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

solutions

Q6
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square,
solutions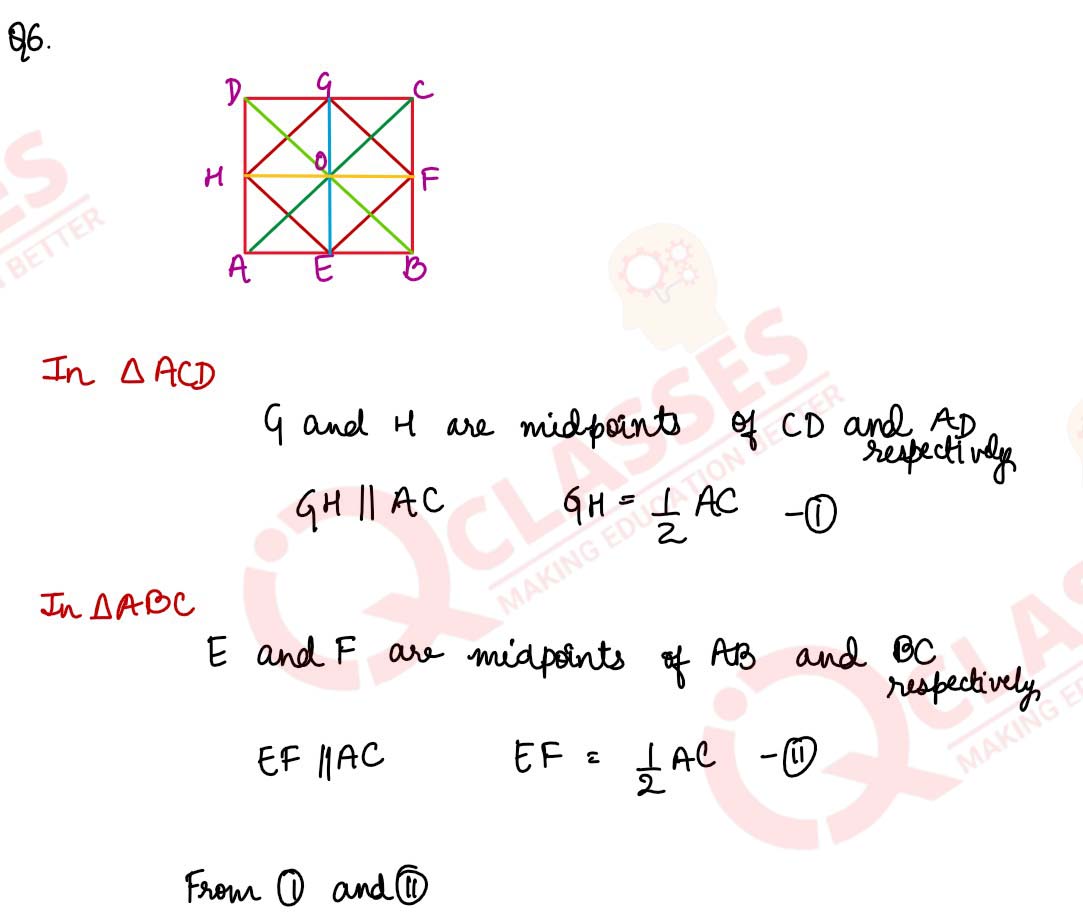


solutions



Q7
In the adjoining figure, AD and BE are medians of ∆ABC. If DF U BE, prove that CF = 1/4 AC.
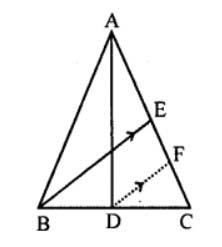
solutions

solutions

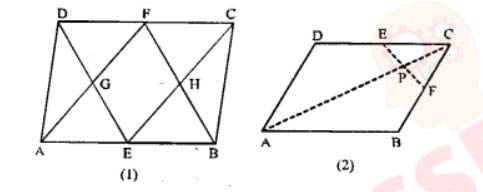
Q8
(a) In the figure (1) given below, ABCD is a parallelogram. E and F are mid-points of the sides AB and CO respectively. The straight lines AF and BF meet the straight lines ED and EC in points G and H respectively. Prove that
(i) ∆HEB = ∆HCF
(ii) GEHF is a parallelogram.
(b) In the diagram (2) given below, ABCD is a parallelogram. E is mid-point of CD and P is a point on AC such that PC = 1/4 AC. EP produced meets BC at F. Prove that
(i) F is mid-point of BC (ii) 2EF = BD
solutions
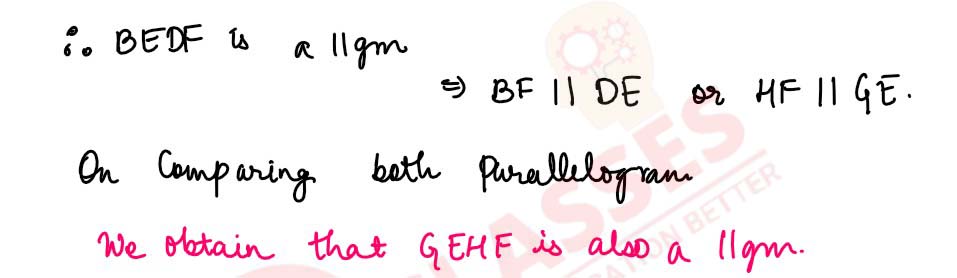
(i) ∆HEB = ∆HCF
(ii) GEHF is a parallelogram.
(b) In the diagram (2) given below, ABCD is a parallelogram. E is mid-point of CD and P is a point on AC such that PC = 1/4 AC. EP produced meets BC at F. Prove that
(i) F is mid-point of BC (ii) 2EF = BD

solutions

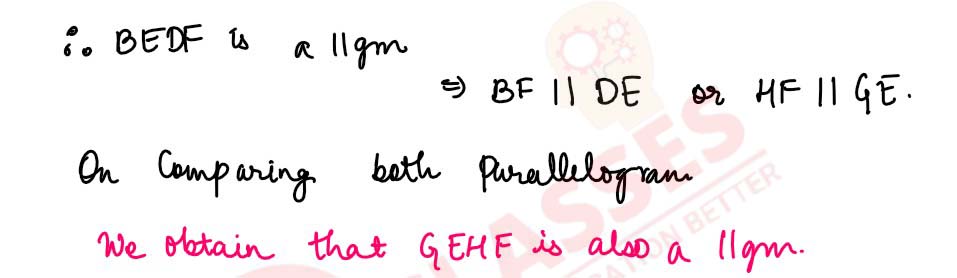
Q9
ABC is an isosceles triangle with AB = AC. D, E and F are mid-points of the sides BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
solutions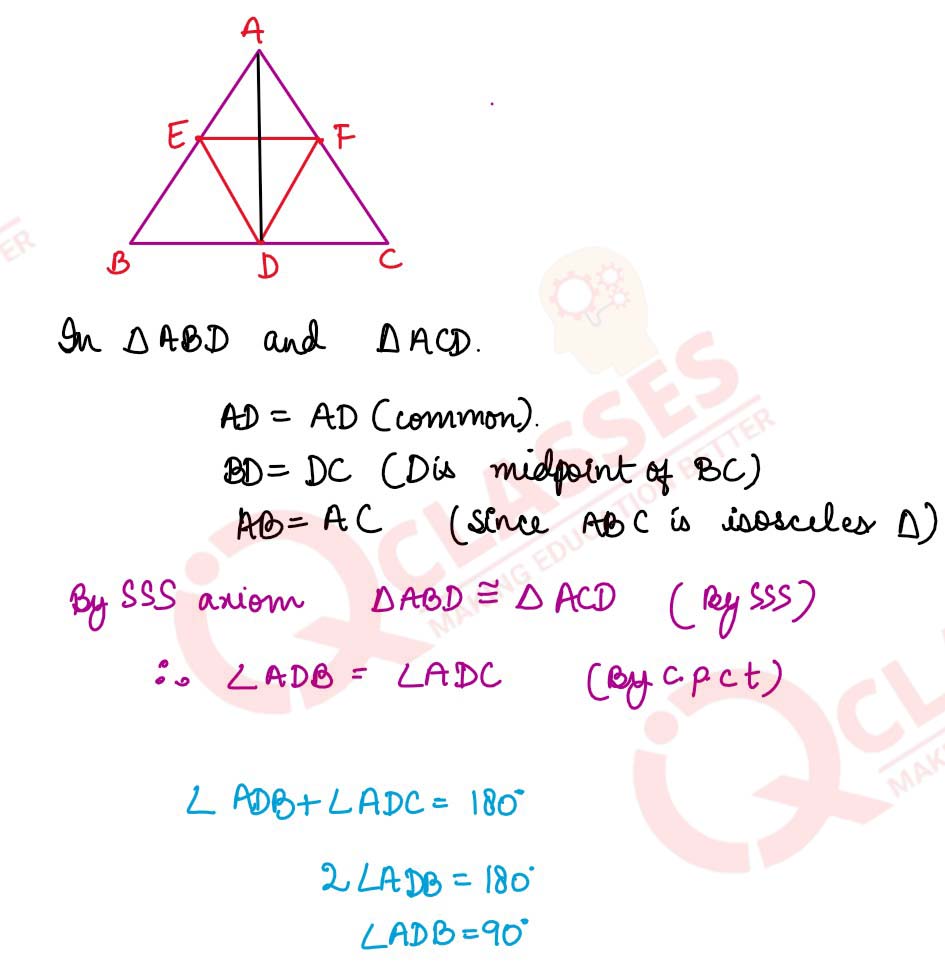

solutions


Q10
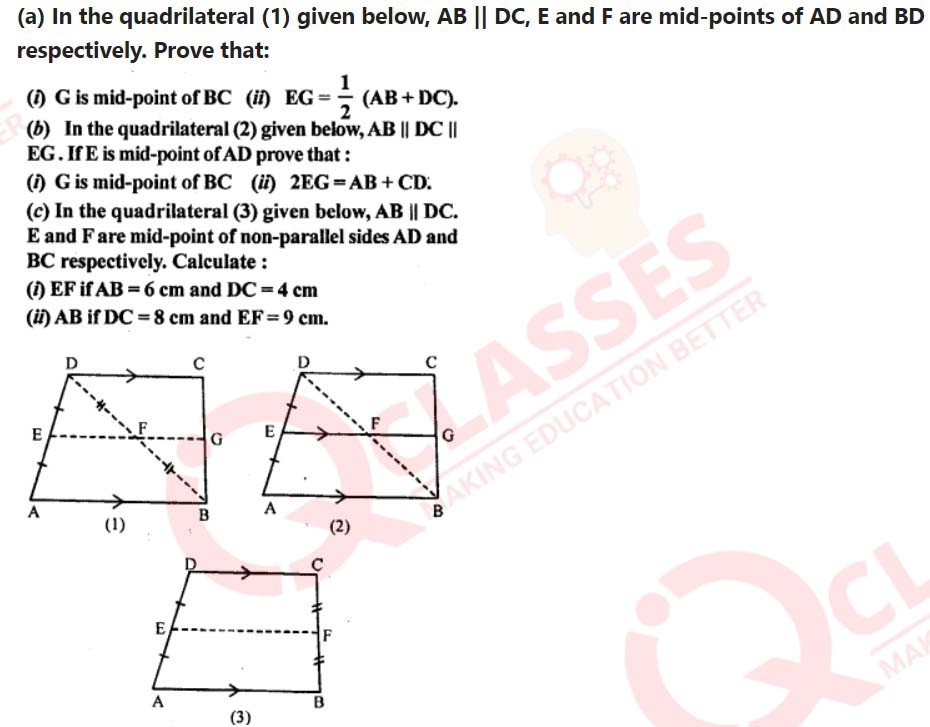
solutions


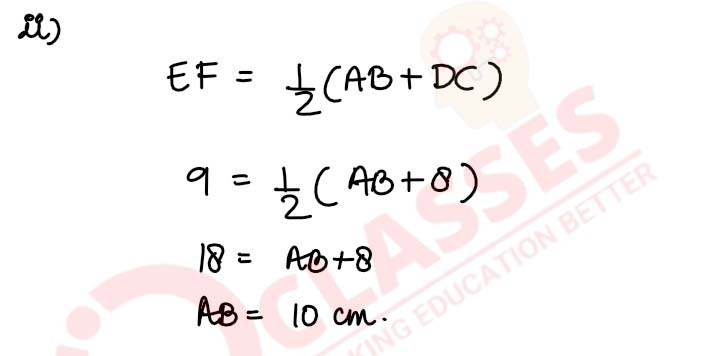

solutions



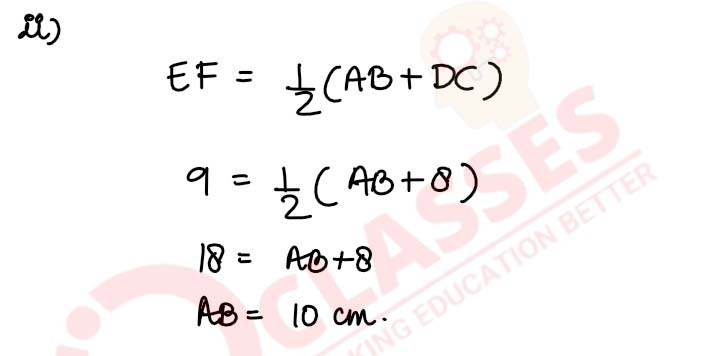
Q11
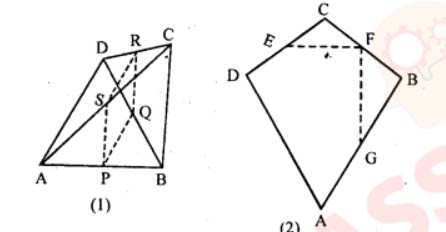
(a) In the quadrilateral (1) given below, AD = BC, P, Q, R and S are mid-points of AB, BD, CD and AC respectively. Prove that PQRS is a rhombus.
(b) In the figure (2) given below, ABCD is a kite in which BC = CD, AB = AD, E, F, G are mid-points of CD, BC and AB respectively. Prove that:
(i) ∠EFG = 90 (ii) The line drawn through G and parallel to FE bisects DA
solutions
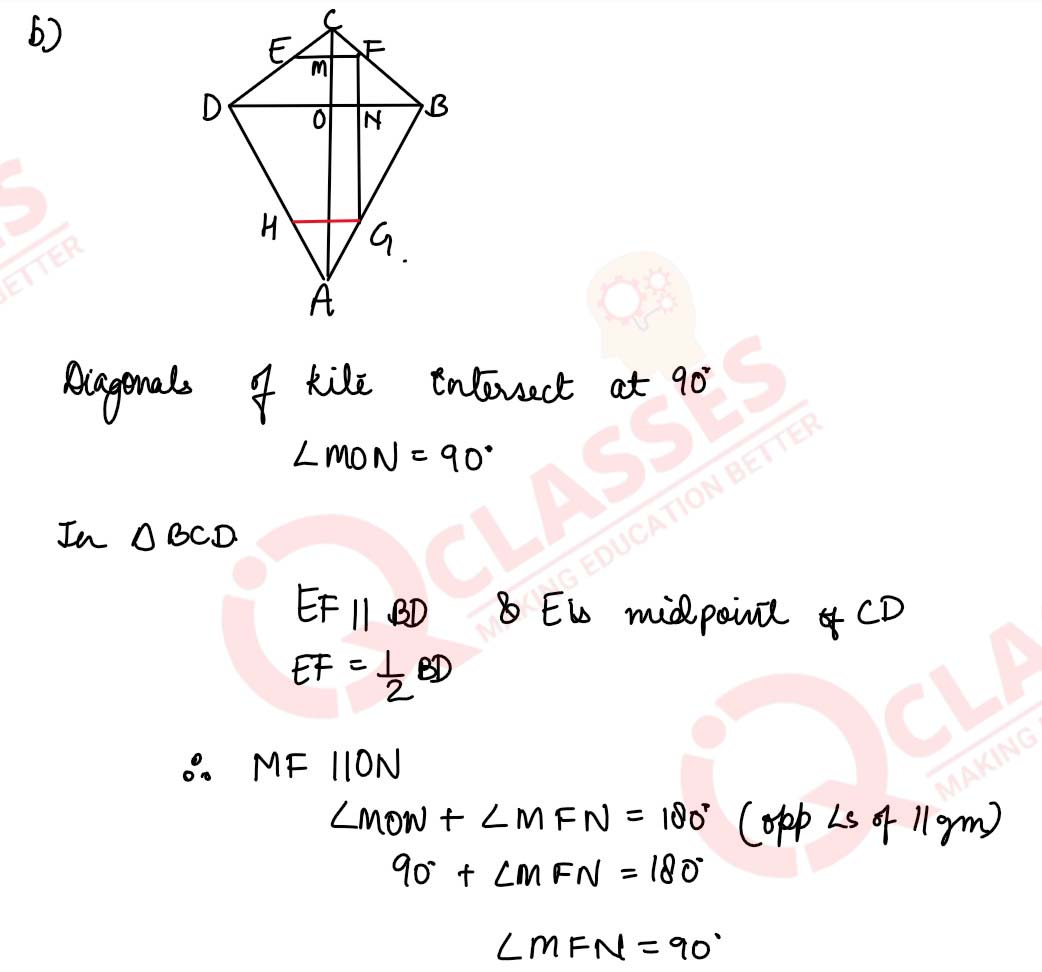

(b) In the figure (2) given below, ABCD is a kite in which BC = CD, AB = AD, E, F, G are mid-points of CD, BC and AB respectively. Prove that:
(i) ∠EFG = 90 (ii) The line drawn through G and parallel to FE bisects DA

solutions



Q12
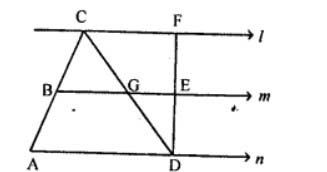
In the adjoining figure, the lines l, m and n are parallel to each other, and G is mid-point of CD. Calculate:
(i) BG if AD = 6 cm
(ii) CF if GE = 2.3 cm
(iii) AB if BC = 2.4 cm
(iv) ED if FD = 4.4 cm.
solutions
(i) BG if AD = 6 cm
(ii) CF if GE = 2.3 cm
(iii) AB if BC = 2.4 cm
(iv) ED if FD = 4.4 cm.

solutions
