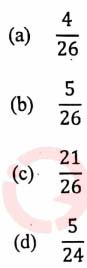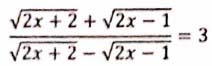Maximum Marks: 80
Time allowed: Two and half hours
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown, and must be done on the same sheet as
the rest of the answer.
Omission of essential working will result in loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ]
Mathematical tables are provided.
Section-A
(Attempt all questions from this Section.)
Question 1
Choose the correct answers to the questions from the given options.
(Do not copy the questions, write the correct answers only.)
(i) 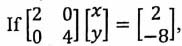 the value of x and y respectively are:
the value of x and y respectively are:
(a) 1,-2
(b) -2.1
(c) 1,2
(d) -2,-1
View
Solution
(ii) If x —2 isa factor of x2 — kx — 12, then the value of k is:
(a) 3
(b) 2
(c) -2
(d) -3
View
Solution
(iii) In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and
∠SPQ = 60° then ∠PSQ is equal to:

(a) 40°
(b) 30°
(c) 60°
(d) 90°
View
Solution
(iv) A letter is chosen at random from all the letters of the English alphabets. The
probability that the letter chosen is a vowel, is:
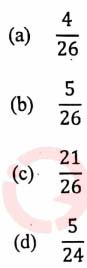
View
Solution
(v) If 3 is a root of the quadratic equation x2 — px + 3 = 0 then p is equal to:
(a) 4
(b) 3
(c) 5
(d) 2
View
Solution
(vi) In the given figure ∠BAP = ∠DCP = 70°, PC = 6 cm and CA = 4 cm, then PD : DB is
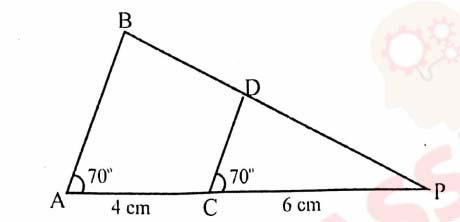
(a) 5:3
(b) 3:5
(c) 3:2
(d) 2:3
View
Solution
(vii) The printed price of an article is Rs 3080. If the rate of GST is 10% then the GST
charged is:
(a) Rs 154
(b) Rs 308
(c) Rs 30.80
(d) Rs 15.40
View
Solution
(viii) (1 + sinA) (1 - sinA) is equal to:
(a) cosec2A
(b) sin2A
(c) sec2A
(d) cos2A
View
Solution
(ix) The coordinates of the vertices of △ABC are respectively (-4, -2), (6, 2) and (4, 6).
The centroid G of △ABC is:
(a) (2,2)
(b) (2, 3)
(c) (3,3)
(d) (0,-1)
View
Solution
(x) The nth term of an Arithmetic Progression (A.P.) is 2n + 5. The 10th term is:
(a) 7
(b) 15
(c) 25
(d) 45
View
Solution
(xi) The mean proportional between 4 and 9 is:
(a) 4
(b) 6
(c) 9
(d) 36
View
Solution
(xii) Which of the following cannot be determined graphically for a grouped frequency
distribution?
(a) Median
(b) Mode
(c) Quartiles
(d) Mean
View
Solution
(xiii) Volume of a cylinder of height 3 cm is 48π. Radius of the cylinder is:
(a) 48cm
(b) 16cm
(c) 4m
(d) 24cm
View
Solution
(xiv) Naveen deposits Rs 800 every month in a recurring deposit account for 6 months. If
he receives Rs 4884 at the time of maturity, then the interest he earns is:
(a) Rs 84
(b) Rs 42
(c) Rs 24
(d) Rs 284.
View
Solution
(xv) The solution set for the inequation 2x + 4 ≤ 14, x ∈ W is:
(a) {1, 2,3, 4, 5}
(b) {0, 1, 2, 3, 4, 5}
(c) {1, 2,3, 4}
(d) {0, 1,2, 3, 4}
View
Solution
Question 2
(i) Find the value of ‘a’ if x - a is a factor of the polynomial 3x3 +
x2 - ax - 81.
(ii) Salman deposits Rs 1000 every month in a recurring deposit account for 2 years.
If he receives Rs 26000 on maturity, find:
(a) the total interest Salman earns.
(b) the rate of interest.
(iii) In the given figure O, is the centre of the circle. CE is a tangent to the circle at A.
If ∠ABD = 26°, then find: 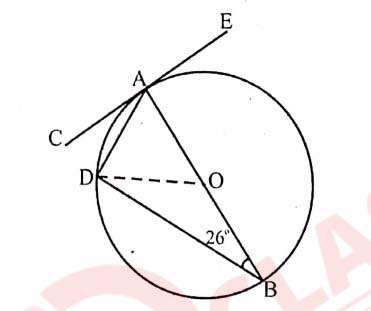
(a) ∠BDA
(b) ∠BAD
(c) ∠CAD
(d) ∠ODB
View
Solution
Question 3
(i) Solve the following quadratic equation:
x2+4x-8=0 .
Give your answer correct to one decimal place.
(Use mathematical tables if necessary.)
(ii) Prove the following identity:
(sin2 θ — 1)(tan2θ + 1) + 1 = 0
(iii) Use graph sheet to answer this question. Take 2 cm = 1 unit along both the axes.
(a) Plot A, B, C where A(0, 4), B(I, 1) and C(4, 0)
(b) Reflect A and B on the x-axis and name them as E and D respectively.
(c) Reflect B through the origin and name it F. Write down the coordinates of F.
(d) Reflect B and C on the y-axis and name them as H and G respectively.
(e) Join points A, B, C, D, E, F, G, H and A in order and name the closed figure
formed.
View
Solution
Section-B
(Attempt any four questions from this Section.)
Question 4
(i)

(ii) ABC is a triangle whose vertices are A(1, -1), B(0, 4) and C(-4, 4).
D is the midpoint of BC. Find the:
(a) coordinates of D.
(b) equation of the median AD.
(iii) In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced
meets the tangent at P. AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
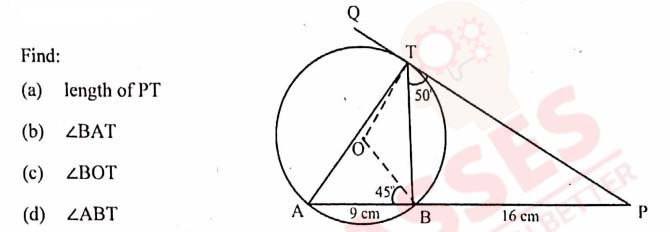
View
Solution
Question 5
(i) Mrs. Arora bought the following articles from a departmental store: 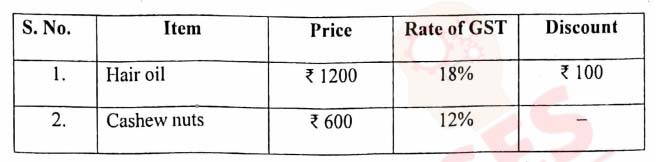
Find the:
(a) Total GST paid.
(b) Total bill amount including GST.
(ii) Solve the following inequation. Write down the solution set and represent it on the
real number line.
-5(x-9) ≥ 17 - 9x > x+2, x∈R
(iii)In the given figure, AC // DE // BE.
If AC = 24 cm, EG=8 cm, GB=16 cm, BF=30 cm.

(a) Prove △GED ~ △GBF
(b) Find DE
(c) DB:AB
View
Solution
Question 6
(i) The following distribution
gives the daily wages of 60 workers of a factory.

Use graph paper to answer this question.
Take 2 cm = 100 along one axis and 2 cm = 2 workers along the other axis.
Draw a histogram and hence find the mode of the given distribution.
(ii) The 5th term and the 9th term of an Arithmetic Progression are 4 and —12 respectively.
Find:
(a) the first term
(b) common difference
(c) sum of 16 terms of the AP.
(iii) A and B are two points on the x-axis and y-axis respectively.

(a) Write down the coordinates of A and B.
(b) Pisa point on AB such that AP : PB = 3 : 1. Using section formula find the
coordinates of point P.
(c) Find the equation of a line passing through P and perpendicular to AB.
View
Solution
Question 7
(i) A bag contains 25 cards, numbered through 1 to 25. A card is drawn at random. What
is the probability that the number on the card drawn is:
(a) multiple of 5
(b) a perfect square
(c) a prime number?
(ii) A man covers a distance of 100 km, travelling with a uniform speed of x km/hr. Had
the speed been 5 km/hr more it would have taken 1 hour less. Find x the original
speed.
(iii) As solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height
4 cm. The solid is immersed completely in a cylindrical container filled with water
to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water
level.
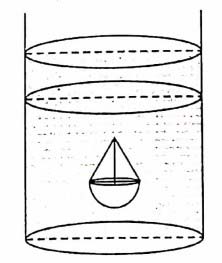
View
Solution
Question 8
(i) The following table gives the marks scored by a set of students in an examination.
Calculate the mean of the distribution by using the short cut method.
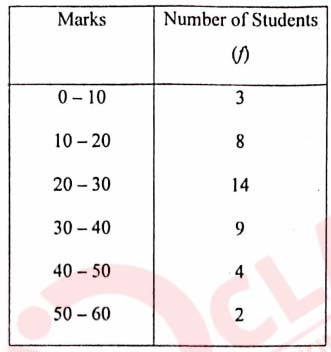
(ii)
What number must be added to each of the numbers 4, 6, 8, 11 in order to get the four
numbers in proportion?
(iii) Using ruler and compass construct a triangle ABC in which AB = 6 cm, ∠BAC =120°
and AC = 5 cm. Construct a circle passing through A, B and C. Measure and write
down the radius of the circle.
View
Solution
Question 9
(i) Using Componendo and Dividendo solve for x:
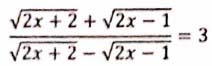
(ii) Which term of the Arithmetic Progression (A.P.) 15, 30, 45, 60... is 300?
Hence find the sum of all the terms of the Arithmetic Progression (A.P.)
(iii) From the top of a tower 100 m high a man observes the angles of depression of two
ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot
of the tower and the ships are in the same horizontal line find the distance between
the two ships A and B to the nearest metre.
(Use Mathematical Tables for this question.)

View
Solution
Question 10
(i) Factorize completely using factor theorem:
2x - x2 - 13x - 6
(ii) Use graph paper to answer this question.
During a medical checkup of 60 students in a school, weights were recorded as
follows:

Taking 2 cm = 2 kg along one axis and 2 cm = 10 students along the other axis draw
an ogive. Use your graph to find the:
(a) median
(b) upper Quartile
(c) number of students whose weight is above 37 kg
View
Solution
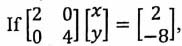 the value of x and y respectively are:
the value of x and y respectively are: