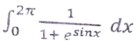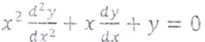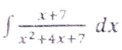Class 12 ISC Maths Boards Paper 2024
Maximum Marks: 80
Time Allowed: Two hours
(Candidates are allowed additional 15 minutes for only reading the paper.
They must NOT start writing during this time).
Section A is compulsory, Attempt any four questions from Section B.
The intended marks for questions or paris of questions are given in brackets []
Section-A
Question
1
In subparts (i) to (x) choose the correct options and in subparts (xi) to (xv), answer the questions as instructed.
(i) Let L be a set of all straight lines in a plane. The relation R on L defined as
'perpendicular to' is:
(a) Symmetric and Transitive
(b) Transitive
(c) Symmetric
( d) Equivalence
Solution
(ii) The order and the degree of differential equation:
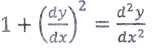
(a) 2 and 3/2
(b) 2 and 3
(c) 3 and 4
(d) 2 and 1
Solution
(iii) Let A be a non-empty set
Statement 1: Identity relation on A is Reflexive.
Statement 2: Every Reflexive relation on A is an Identity relation.
(a) Both the statements are true.
(b)
Both the statements are false.
(c)
Statement 1 is true and Statement 2 is false.
(d)
Statement 1 is false and Statement 2 is true.
Solution
(iv) The graph of the function f is shown below
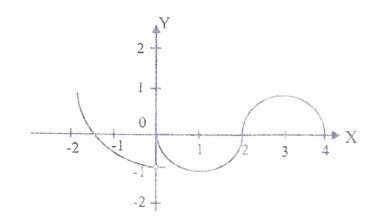
Of the following options, at what values of x is the function ƒ NOT differentiable?
(a)
At x = 0 and x = 2
(b)
At x= 1 and x = 3
(c)
At x=-1 and x = 1
(d) At x=-1.5 and x = 1.5
Solution
(v) The value of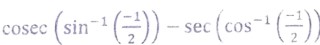 
is equal to :
(a) -4
(b) 0
(c) -1
(d) 4
Solution
(vi) The value of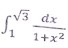 
is
(a) π/2
(b) 2π/3
(c) π/6
(d) π/12
Solution
(vii) Assertion : Let the matrices 
be such that A100B = BA100
Reason: AB = BA implies AnB = BAn for all positive integers n.
(a) Both Assertion and Reason are true and Reason is the correct explanation
for Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation of assertion.
(c) Assertion is true and Reason is false
(d) Assertion is false and Reason is true
Solution
(viii) If ∫(cot x - cosec2x) exdx = exf (x) + c then f (x) will be
(a) cot x + cosec x
(b) cot2x
(c) cot x
(d) cosec x
Solution
(ix) In which one of the following intervals is the function f(x) = x3- 12x
increasing?
(a) (-2,2)
(b) (- ∞, - 2) U ( 2, ∞)
(c) (- 2, ∞)
(d) (-∞, 2)
Solution
(x) If A and B are symmetric matrices of the same order, then AB - BA is
(a) Skew symmetric matrix
(b) Symmetric matrix
(c) Diagonal matrix
(d) Identity matrix
Solution
(xi) Find the derivative of y = log x + 1/x with respect to x
Solution
(xii) Teena is practising for an upcoming Rifle Shooting tournament. The probability of
her shooting the target in the 1st, 2nd, 3rd and 4th shots are 0.4, 0·3, 0·2 and 0·1
respectively. Find the probability of at least one shot of Teena hitting the target
Solution
(xiii) Which one of the following graphs is a function of x?
Solution
(xiv) Evaluate 
Solution
(xv) Given that 1/x + 1/y = 1/12 and y decreases at a rate of
1 cms-1, find the rate of change of x when x = 5 cm and y= 1 cm
Solution
Section-B
Question 2
(i) Let f:R - {-1/3} → R - {0} be defined as f(x)= 5/3x+1 is invertible.Find f-1(x)
OR
(ii) If f:R → R is defined by f(x) = 2x-7/4 show that f(x) is one-one and onto
Solution
Question 3
Find the value of the determinant given below, without expanding it at any stage.
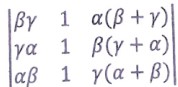
Solution
Question 4
(i) Determine the value of k for which the function is continous at x=3
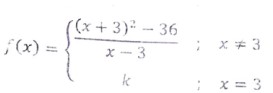
OR
(ii)
Find a point on the curve y = (x-2)2 at which the tangent is parallel to the line
joining the chord through the points (2, 0) and (4,4).
Solution
Question 5
Question 6
Question 7
Question 8
(i) Solve for for x:
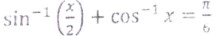
OR
(ii) If sin-1x + sin-1y + sin-1z = π, show that x2 - y2 - z2+2yz√(1 − x2) = 0
Solution
Question 9
Question 10
A jewellery seller has precious gems in white and red colour which he has put in three
boxes. The distribution of these gems is shown in the table given below:
He wants to gift two gems to his mother. So, he asks her to select one box at random and pick out any two gems one after the other without replacement from the selected box. The mother selects one white and one red gem. Calculate the probability that the gems drawn are from Box II.
Solution
Question 11
A furniture factory uses three types of wood namely, teakwood, rosewood and satinwood for manufacturing three types of furniture, that are, table, chair and cot. The wood requirements (in tonnes) for each type of furniture are given below:
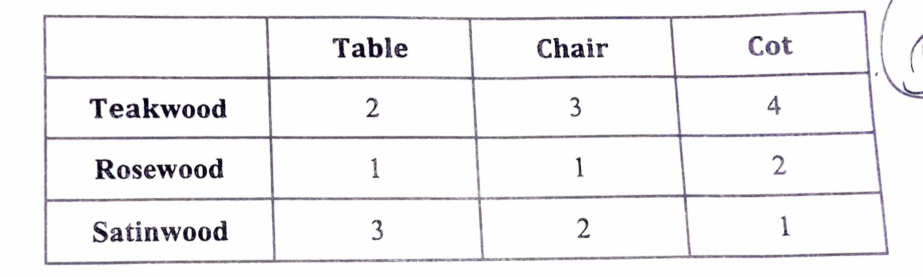
It is found that 29 tonnes of teakwood, 13 tonnes of rosewood and 16 tonnes of satinwood are available to make all three types of furniture.
Using the above information, answer the following questions:
(i) Express the data given in the table above in the form of a set of simultaneous equations.
(ii) Solve the set of simultaneous equations formed in subpart (1) by matrix method.
(iii) Hence, find the number of table(s),chair(s) and cot(s) produced
Question 12
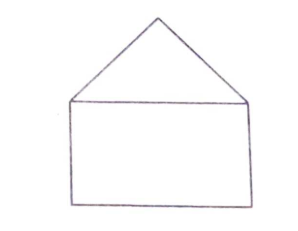
Mrs. Roy designs designs a window in her son's study room so that room gets maximum sunlight.She designs the window in the shape of rectangle sorrounded by an equilateral triangle.If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room
(ii) Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is 'r' cm and height is ‘h’ cm. It has a volume of 20π cm3
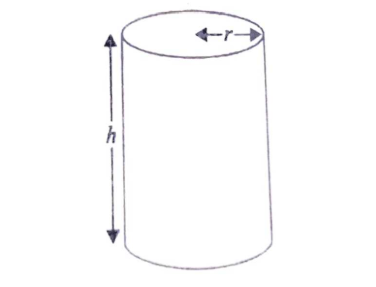
(a) Express ‘h’ in terms of 'r',using the given volume.
(b) Prove that the total surface area of the dustbin is 2πr2+40π/r
(c) Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹2 per cm2 and the cost of painting the curved side is ₹25 per cm2.Find the cost in terms of 'r' for painting the outer surface of the dustbin including the base and top.
(d) Calculate the minimum cost for painting the dustbin
Question 13
(i) Solve the following differential equation:
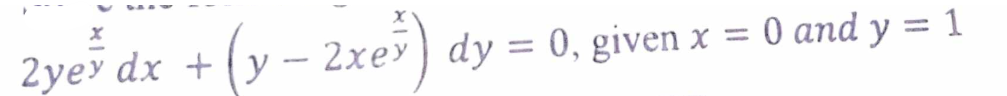
OR
(ii) Solve the following differential equation:
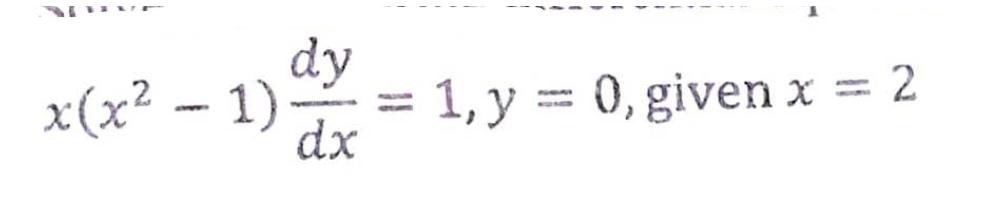
Question 14
A primary school teacher wants to teach the concept of ‘larger number’ to the students of Class 11. To teach this concept, he conducts an activity in his class. He asks the children to select two numbers from a set of numbers given as 2, 3, 4,5 one after the other without replacement. All the outcomes of this activity are tabulated in the form of ordered pairs given below
(i) Complete the table given above.
(ii) Find the total number of ordered pairs having one larger number.
(iii) Let the random variable X denote the larger of two numbers in the ordered pair. Now, complete the probability distribution table for X given below
(iv) Find the value of P(X < 5)
(v) Calculate the expected value of the probability distribution.
Question 15
(i) If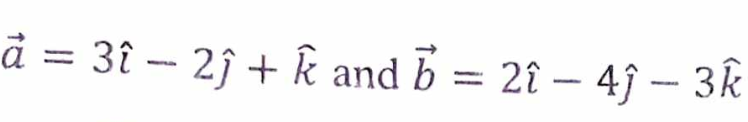 
then the value of 
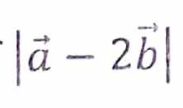will be:
(a) √85
(b) √86
(c) √87
(d) √88
(ii) If a line makes an angle α, β and γ with positive direction of the coordinate axes, then the value of sin2α+ sin2β + sin2γ will be:
(a) 1
(b) 3
(c) -2
(d) 2
(iii) In the figure. given below, if the coordinates of the point P are (a, b, c), then what are the perpendicular distances of P from XY, YZ and ZX planes respectively?
(iv) If a->=2i^+j^+ 2k^ and b-> = 5i^-3j^+ k^, find the projection of b-> on a->
(v) Find a vector of magnitude 20 units parallel to the vector 2i^ + 5j^+ 4k^
Question 16
(i) If a-> x b-> = a-> x c-> where a->, b-> and c-> are non-zero vectors,then prove that either b-> = c-> or a-> and ( b-> - c->) are parallel.
OR
If a-> and b-> are two non-zero vectors such that |a-> x b->| = a-> . b-> , find the angle between a-> and b->
Question 17
A mobile tower is situated at the top of a hill. Consider the surface on which the tower stands as a plane having points A( 1, O, 2), B(3, -1, 1) and C( 1, 2, 1) on it. The mobile tower is tied with three cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at point P(2, 3, 1) as shown in the figure below. The foot of the perpendicular from the point P on the plane is at the point Q(43/29,77/29,9/29)
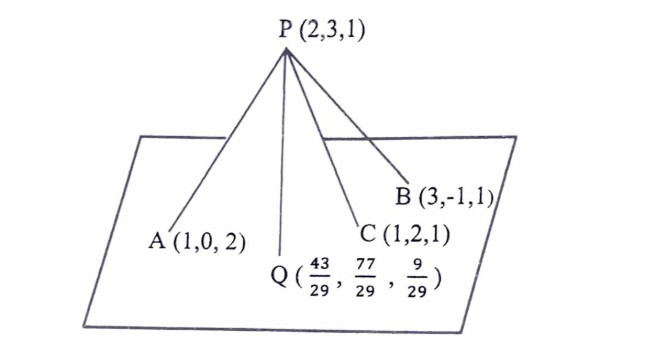
Answer the following questions.
(i) Find the equation of the plane containing the points A, B and C.
(ii) Find the equation of the line PQ.
(iii) Calculate the height of the tower.
Question 18
(i) Using integration, find the area bounded by the curve y2 = 4ax and the line x = a
OR
(ii) Using integration, find the area of the region bounded by the curve y2 =4x and x2= 4y
Section-C
Question 19
(i) A company sells hand towels at manufacture hard ae at ₹100 per unit. The fixed cost for the company to manufacture hand tables ₹35,000 and variable cost is estimated to be 30% of total revenue.What will be the total cost function for manufacturing hand towels?
(a) 35000 + 3x
(b) 35000 + 30x
(c) 35000 + 100x
(d) 35000 + 10x
(ii) If the correlation coefficient of two sets of variables (X,Y) is -3/4 which one of the following statements is true for the same set of variables?
(a) Only one of the two regression lines has a negative coefficient.
(b) Both regression coefficients are positive.
(c) Both regression coefficients are negative.
(d) One of the lines of regression is parallel to the x-axis.
(iii) If the total cost fhnction is given by C = x + 2x3 - 7/2 x2, find the Marginal Average Cost function (MAC)
(iv) The equations of two lines of regression are 4x+3y+7=0 and 3x+4y+8=0. Find the mean value of x and y.
(v) The manufacturer of a pen its selling price at ₹45,and the cost function is C(x)=30x+240.The manufacture will begin to earn profit if he sells more than 16 pens. Why?Give one reason.
Question 20
(i) The Average Cost function associated with producing and marketing x units of an item is given by AC = x+5+36/x
(a) Find the Total Cost function.
(b) Find the range of values of x for which Average Cost is increasing.
OR
A monopolist's demand function is x = 60 - p/5. . At what level of output will marginal revenue be zero?
Question 21
(i) XYZ company plans to advertise some vacancies. The Manager is asked to suggest the monthly salary for these vacancies based on the years of experience.To do so, the Manager studies the years of service and the monthly salary drawn by the existing employees in the company.
Following is the data that the Manager refers to:
(a) Find the regression equation of monthly salary on the years of service.
(b) If a person with 13 years of experience applies for a job in this company, what monthly salary will be suggested by the Manager?
OR
(ii) The line of regression of marks in Statistics (X) and marks in Accountancy (Y) for a class of 50 students is 3y - 5x + 180 = 0. The average score in Accountancy is 44 and the variance of marks in Statistics is (9/16)th of variance of marks in Accountancy.
(a) Find the average score in Statistics.
(b) Find the coefficient of correlation between marks in Statistics and marks in Accountancy
Question 22
Aman has ₹1500 to purchase rice and wheat for his grocery shop. Each sack of rice and wheat costs ₹180 and ₹120 respectively. He can store a maximum number of 10 bags in his shop. He will earn a profit of ₹11 per bag of rice and ₹9 per bag of wheat.
(i) Fonnulate a Linear Programming Problem to maximise Aman's profit.
(ii) Calculate the maximum profit
Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119