Class 10 CBSE Maths Polynomials Important Questions
A polynomial is made up of terms that are only added, subtracted or multiplied. A quadratic polynomial in x with real coefficients is of the form ax² + bx + c, where a, b, c are real numbers with a ≠ 0. Degree – The highest exponent of the variable in the polynomial is called the degree of polynomial.
Q1. Find the zeros of the polynomial 6x2 -3-7x and verify the relationship between the zeros and the coefficients.
Solution

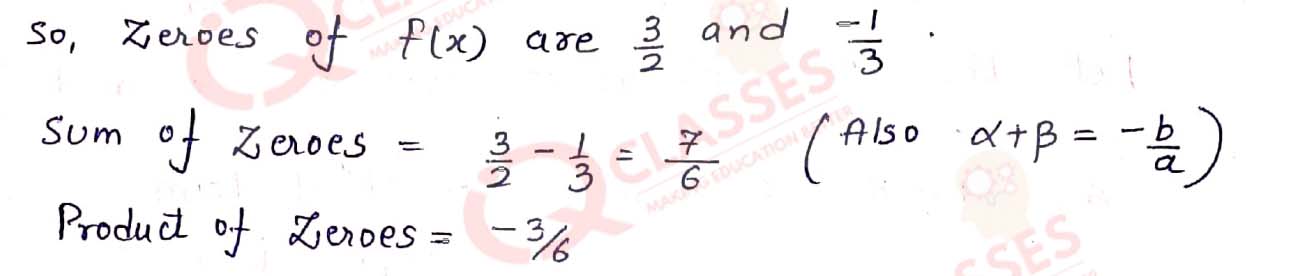
Q2. Find the quadratic polynomial, the sum of whose zeros is √2 and their product is -12. Hence, find the zeros of the polynomial.
Solution


Q3. If the product of the zeros of the polynomial (ax2 — 6x — 6) is 4, find the value of a.
Solution

Q4. If one zero of the polynomial (a2 + 9) x2 + 13x + 6a is reciprocal of the other, find the value of a.
Solution


Q5. Find a cubic polynomial with the sum of its zeros, sum of the products of its zeros taken two at a time and the product of its zeros as 2, —7 and -14 respectively.
Solution


Q6. If the zeros of the polynomial x3 — 3x2 + x + 1 are (a — b), a, (a + b), find a and b.
Solution

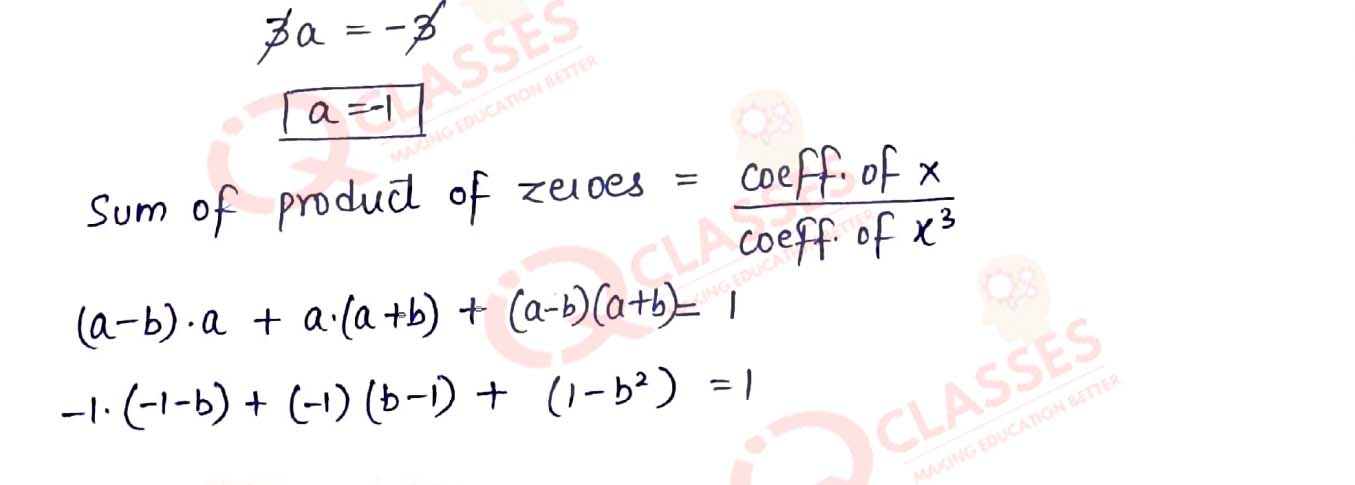

Q7. Find a cubic polynomial whose zeros are 3, 1/2 and -1.
Solution


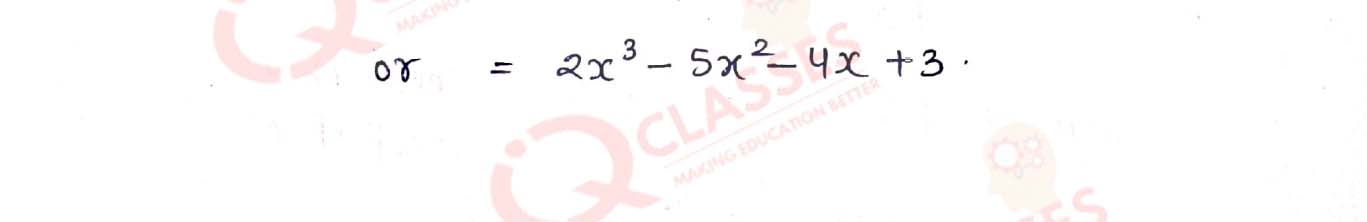
Q8. Divide 5x3 — 13x2 + 21x -14 by (3 - 2x + x2) and verify the division algorithm.
Solution

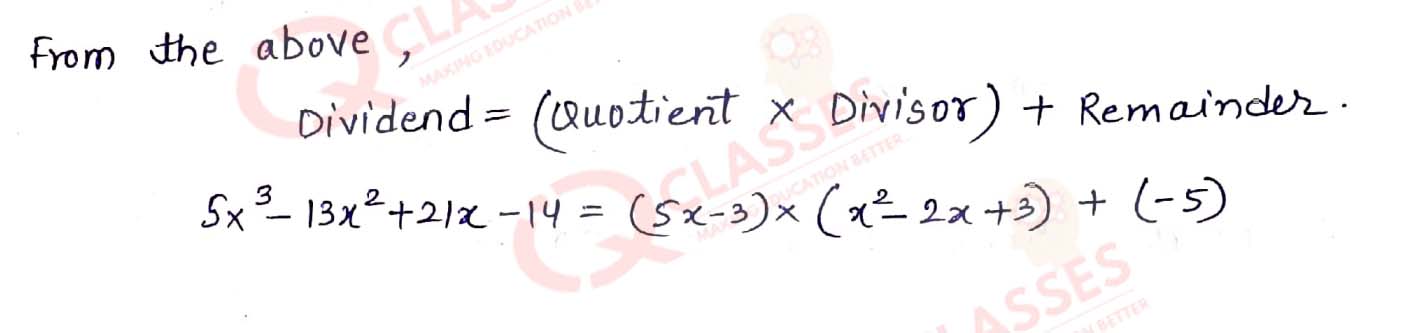
Q9. It being given that 1 is a zero of the polynomial (7x — x3 — 6), find its other zeros.
Solution
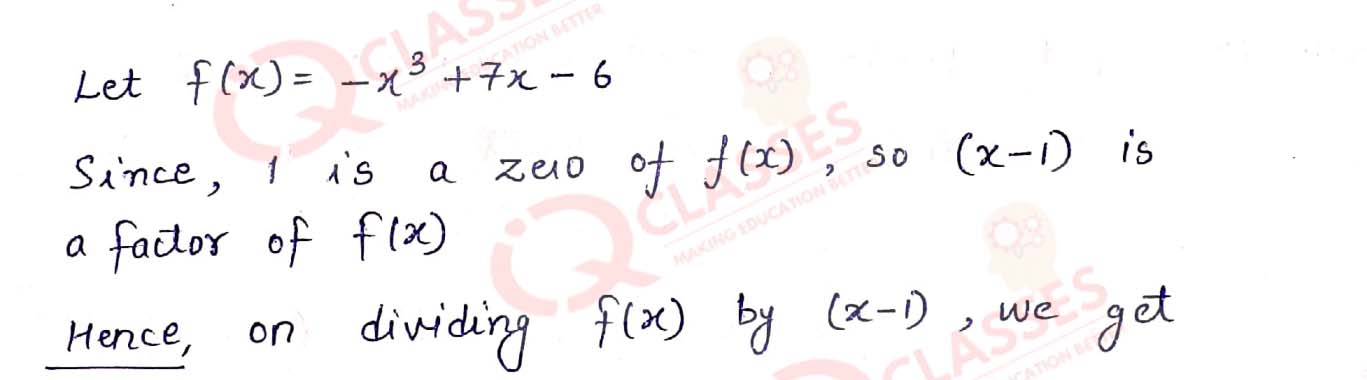
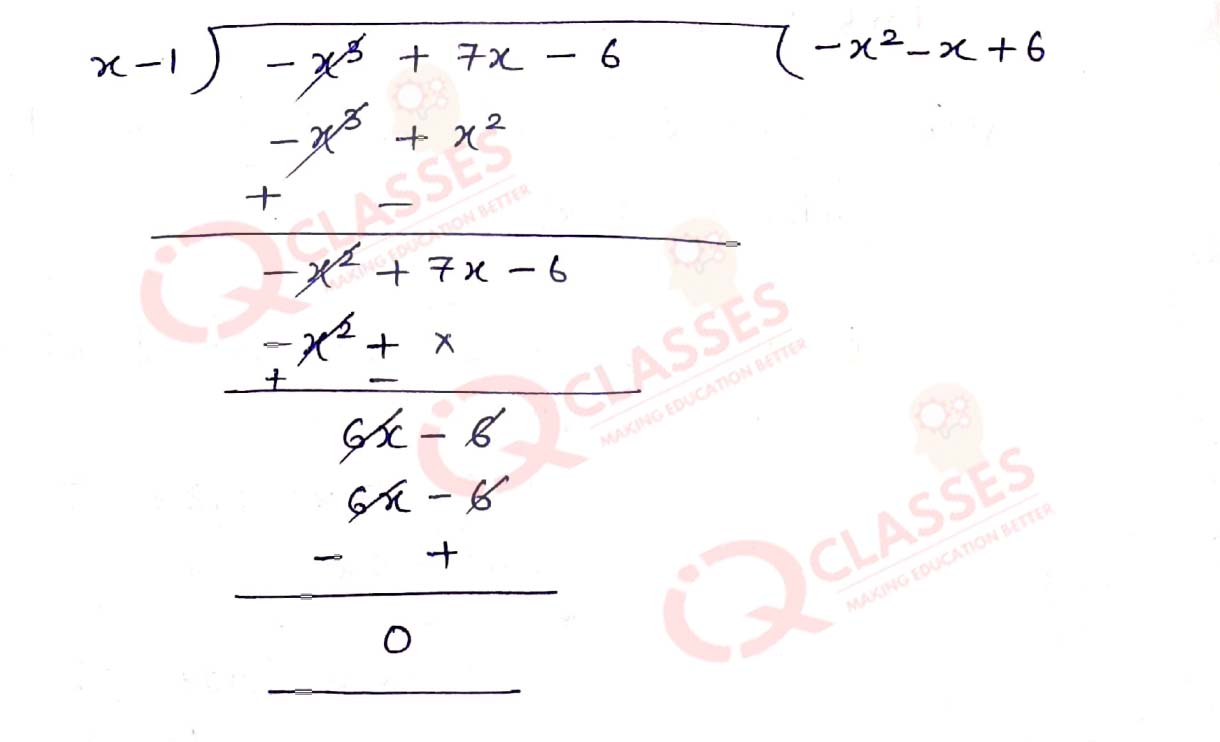
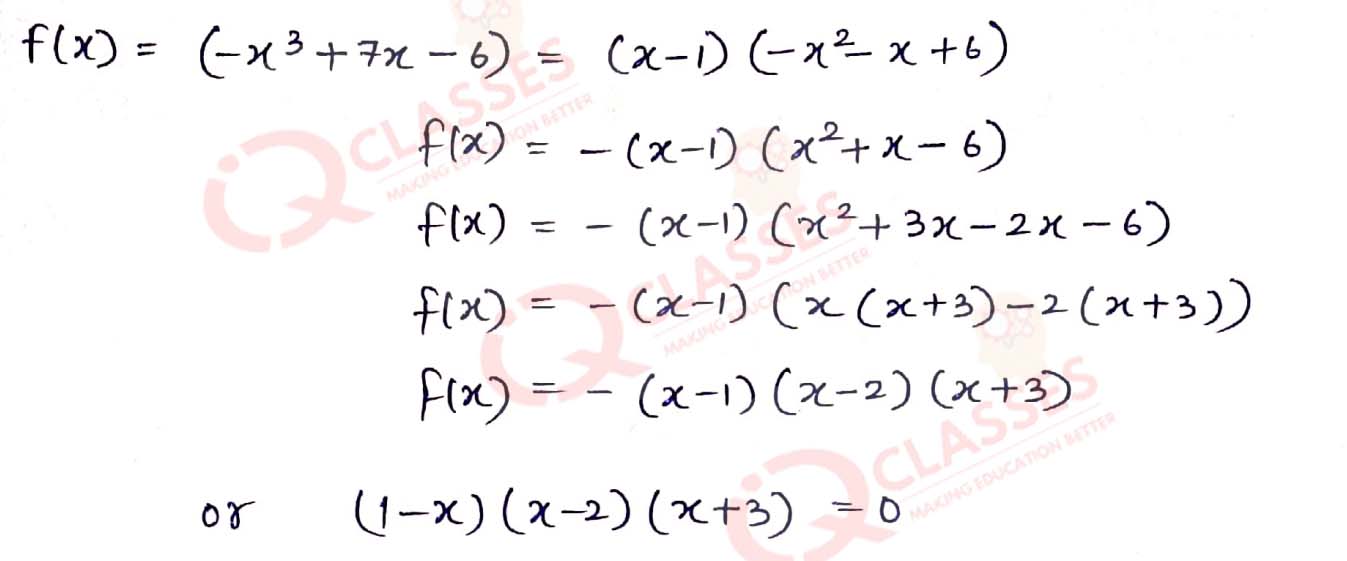

Q10. If two zeros of the polynomial (x4 - 6x3 — 26x2 + 138x — 35) are (2 + √3) and (2 - √3),find other zeros.
Solution

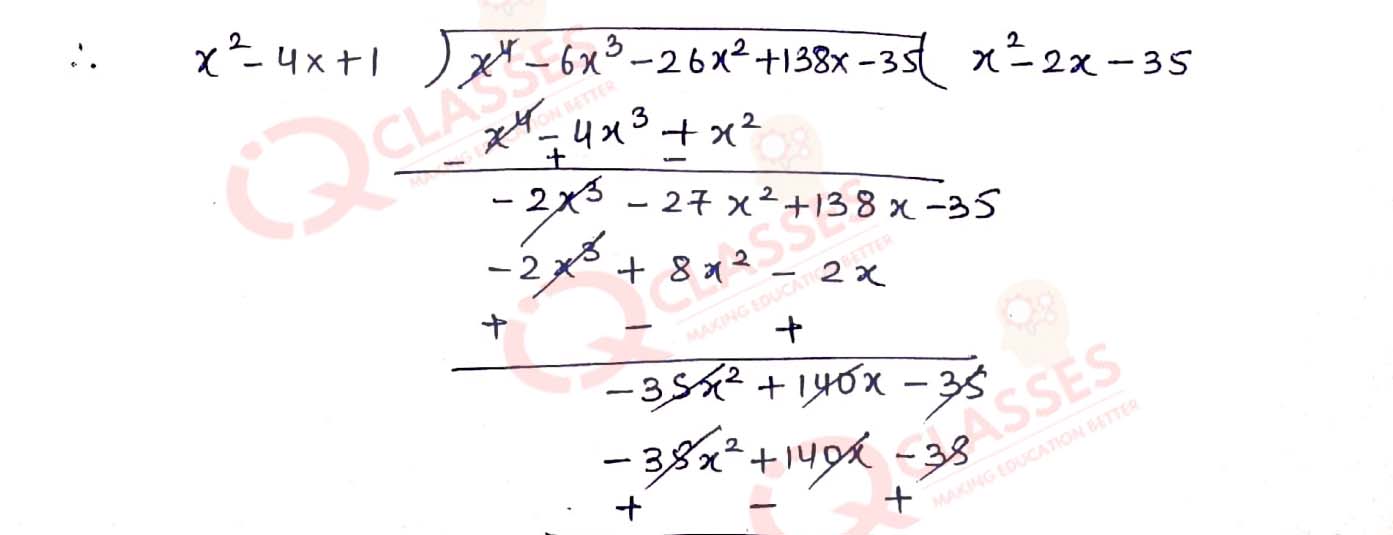

Q11. If α and β are the zeros of the polynomial f(x)= 5x2 — 7x + 1, find the value of (1/α + 1/β)
Solution


Q12. If α and β are the zeros of the polynomial f(x) = x2 + x - 2, find the value of (1/α - 1/β)
Solution
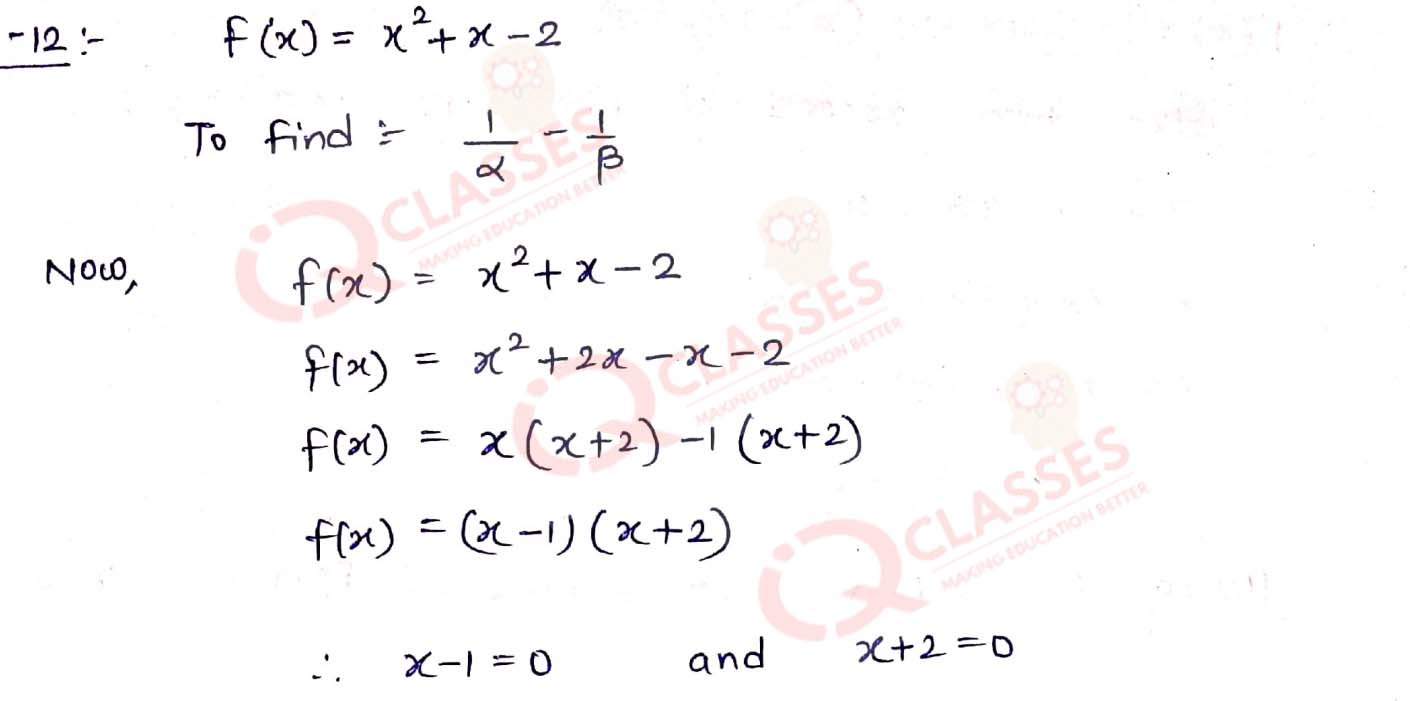
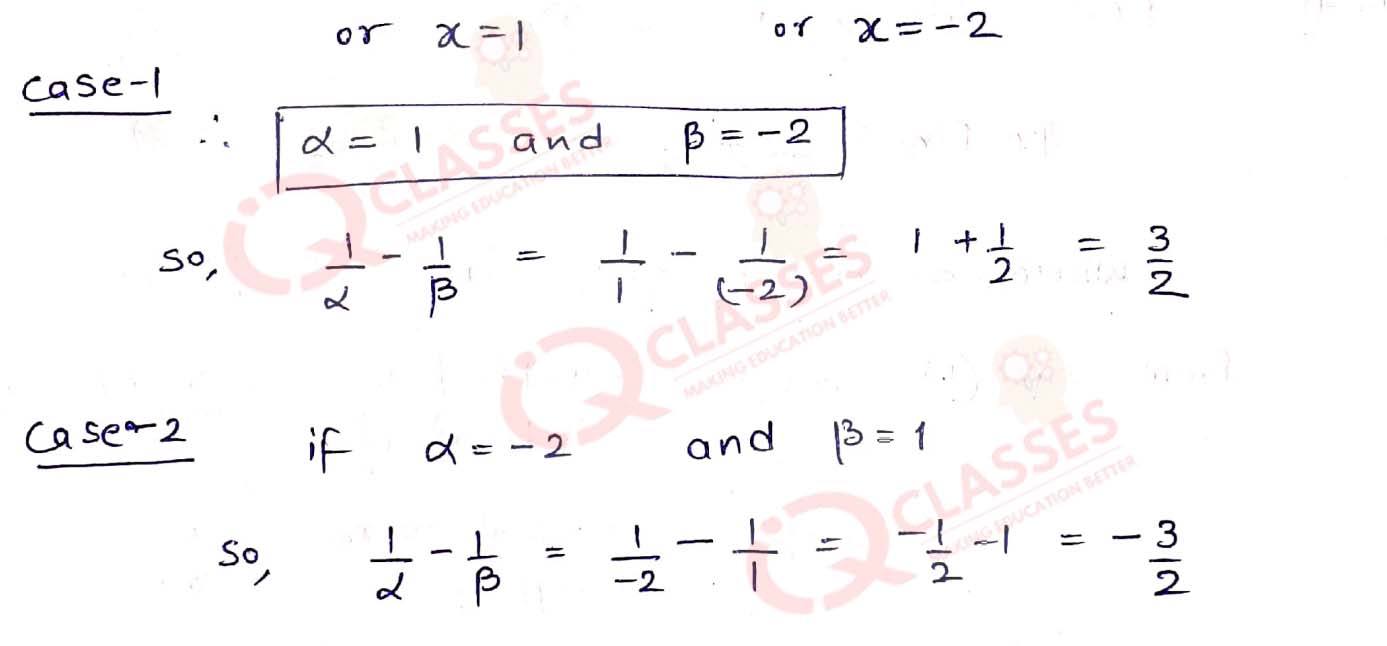
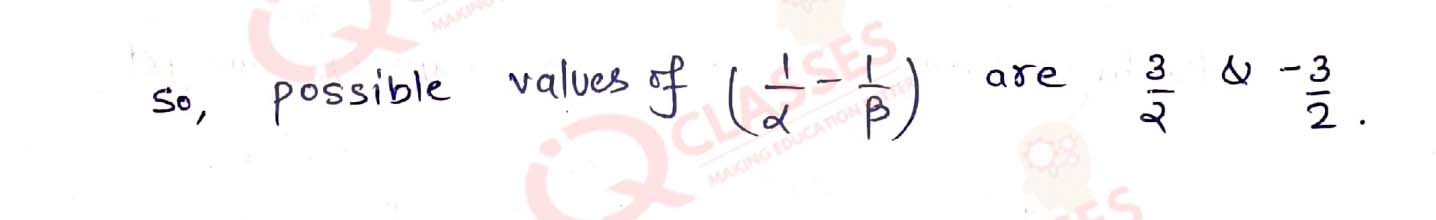
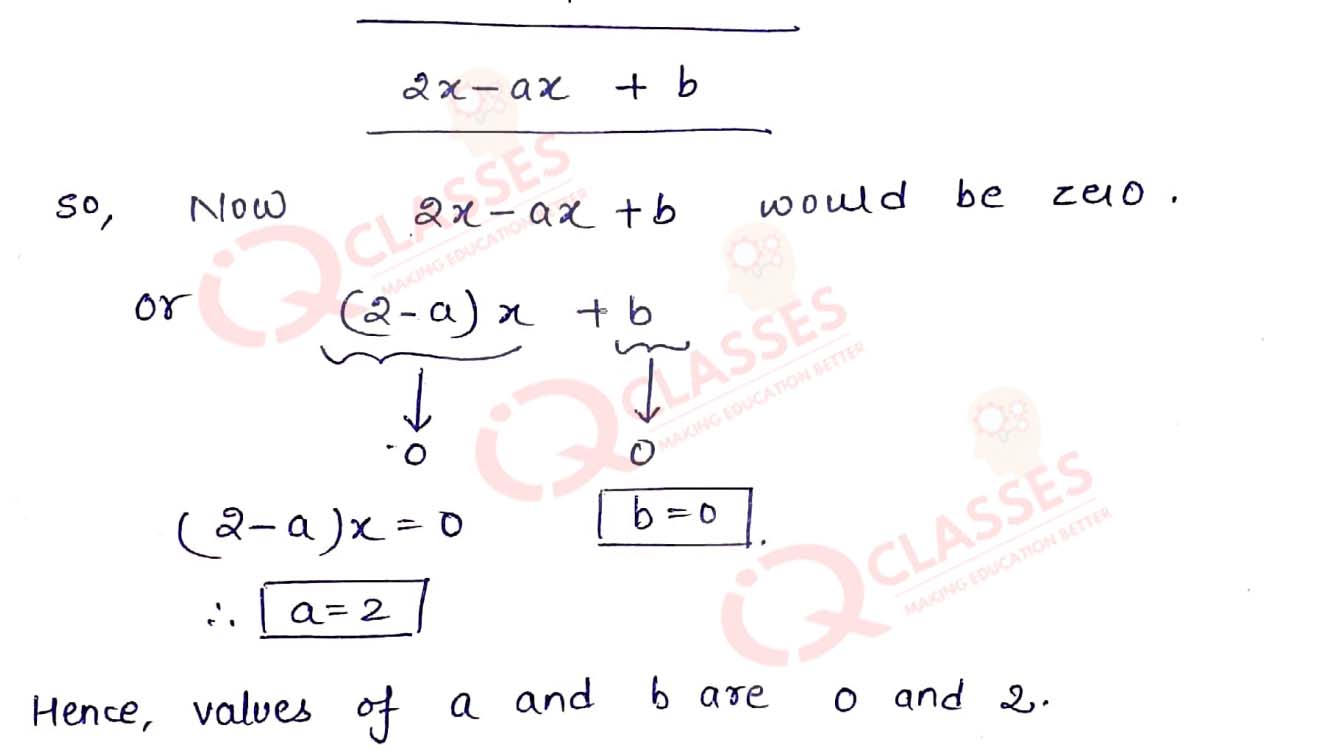
Q13. If x3 + x2 - ax + b is divisible by (x2 — x), write the values of a and b.
Solution

Q14. If (x + a) is a factor of the polynomial 2x2 + 2ax + 5x + 10, find the value of a.
Solution


Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment