Class10 CBSE Maths Important Questions Chapter Quadratic Equations

Class 10 CBSE Maths Quadratic Equations Important Questions

When we equate a quadratic polynomial to a constant, we get a quadratic equation. Any equation of the form p(x) = k, where p(x) is a polynomial of degree 2 and c is a constant, is a quadratic equation.

The standard form of a quadratic equation is ax²+bx+c=0, where a,b and c are real numbers and a≠0. ‘a’ is the coefficient of x². It is called the quadratic coefficient. ‘b’ is the coefficient of x. It is called the linear coefficient. ‘c’ is the constant term.

Select Option

Board Questions

Important Notes

Quadratic Equations Important Questions

Q1(i) (x+2)³=2x(x²-1)

Solution

Q1(ii) x(x+3)+6= (x+2)(x-2)

Solution

Q2 Show that √2 and -2√2 are the root of the equation x²+√2x-4=0

Solution

Q3 Solve: 8x²-22x-21 =0 by the factorisation method.

Solution

Q4 Solve:
x+3 / x+2
=
3x-7 / 2x-3

Solution

Q5 Solve:
14 / x+3
-1=
5 / x+1
,x≠-3,-1

Solution

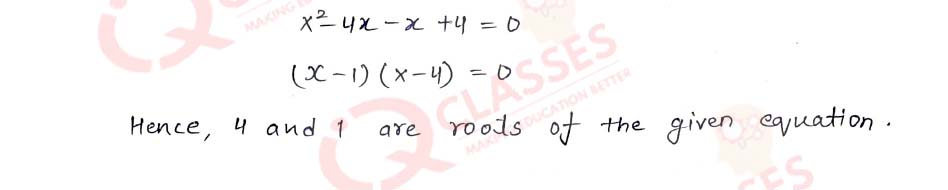
Q6 Solve:
x-2 / x-3
+
x-4 / x-5
=3
1 / 3
,x≠3,5

Solution

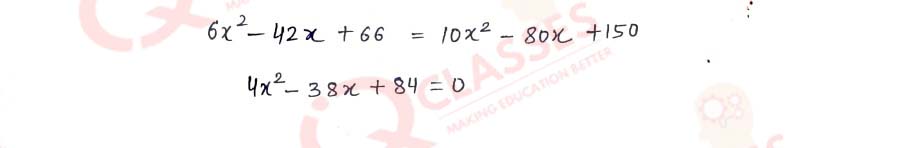
Q7 Solve:
2 / (x+1)
+
3 / 2(x-2)
=
23 / 5x
,x≠0,-1,2

Solution

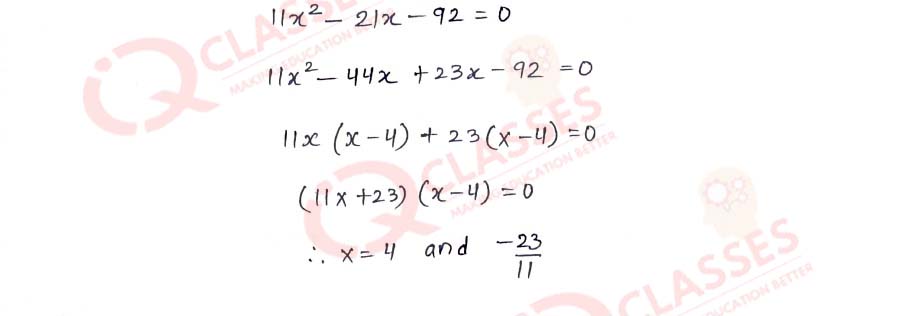
Q8 Solve: 5^(x+1) +5^(2-x) =5³+1

Solution

Q9 Show that the equation 2x² + 5√3x+6 =0 has real roots and solve it.

Solution

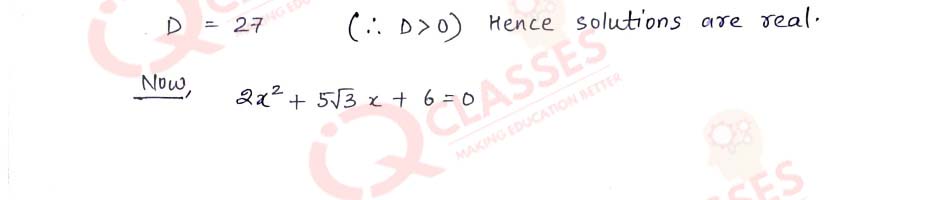
Q10 Using quadratic formula, solve for x:
abx² +(b²-ac)x-bc=0

Solution

Q11 Find the values of k for which the quadratic equation 2x² + kx + 3=0 has two real equal roots.

Solution

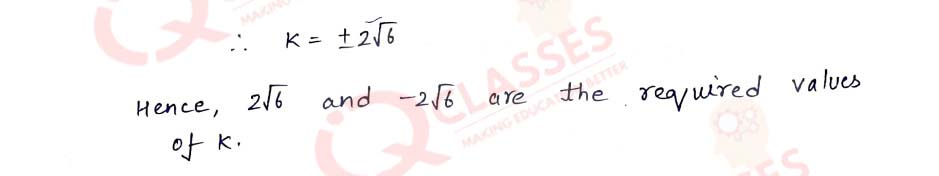
Q12 Determine the positive value of p for which the equations x² +2px+64=0 and x² -8x+2p=0 will both have real roots

Solution

Q13 Find the nonzero value of k for which the quadratic equation kx²+1-2(k-1)x+x² =0has equal roots.Hence,find the roots of the equation

Solution

Q14 If the roots of the equation (b-c)x²+(c—a)x+(a- b)=0 are equal,prove that 2b=a+c

Solution

Q15 Solve the equation x² -(√3 +1)x+ √3 = 0 by the method of completing the square

Solution

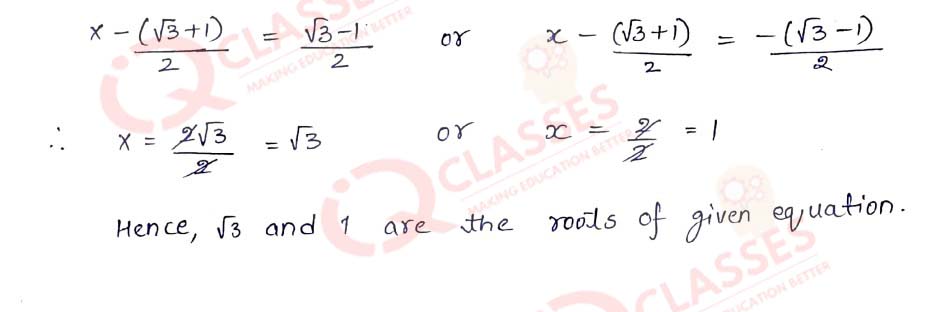
Quadratic Equation (Word Problem)

Q1 The sum of the squares of two consecutive odd numbers is 394. Find the numbers.

Solution

Q2 The difference of two natural numbers is 5 and the difference of their reciprocal is 1/10 . Find the numbers.

Solution

Q3 The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.

Solution

Q4 The numerator of a fraction is 3 less than its denominator. If 2 is added to both of its numerator and denominator then the sum of the fraction and original fraction is 29/20. Find the original fraction.

Solution

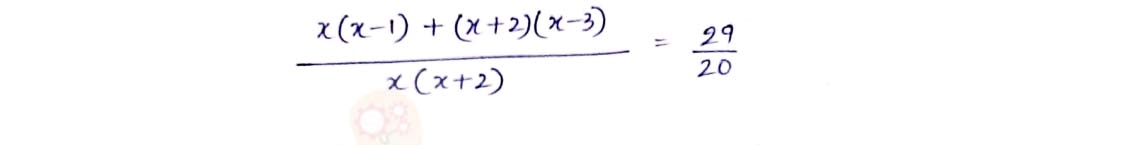
Q5 A two-digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.

Solution

Q6 A bookseller buys a number of books for ₹1760. If he had bought 4 more books for the same amount, each book would have cost ₹22 less. How many books did he buy?

Solution

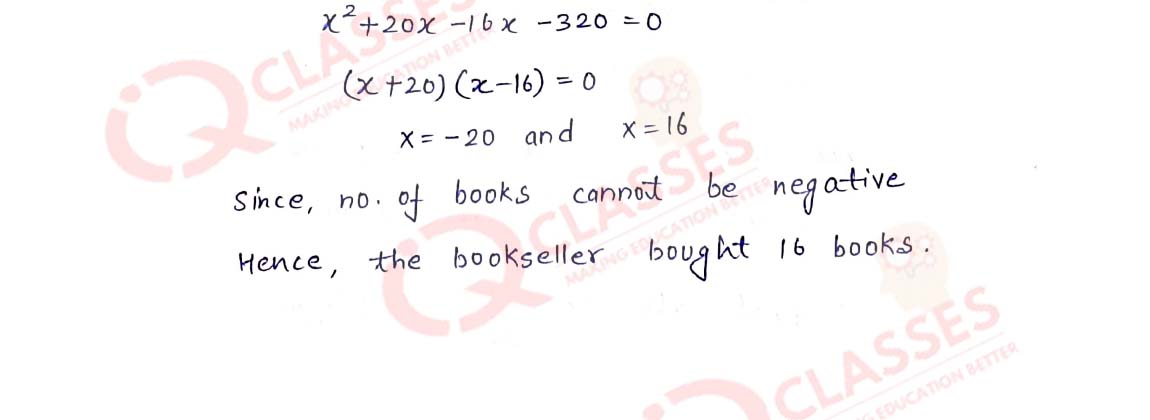
Q7 The total cost of a certain length of a piece of wire is ₹200. If the piece was 5 metres longer and each metre of wire costs ₹2 less, the cost of the piece would have remained unchanged. How long is the piece and what is its original rate per metre?

Solution

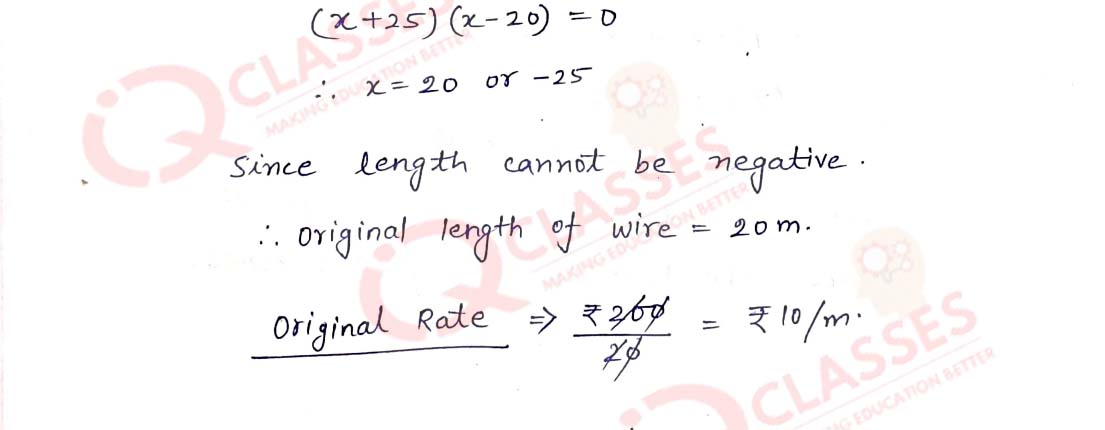
Q8 A girl is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages.

Solution

Q9 The age of a man is twice the square of the age of his son. Eight years hence, the age of the man will be 4 years more than three times the age of his son. Find their present ages.

Solution

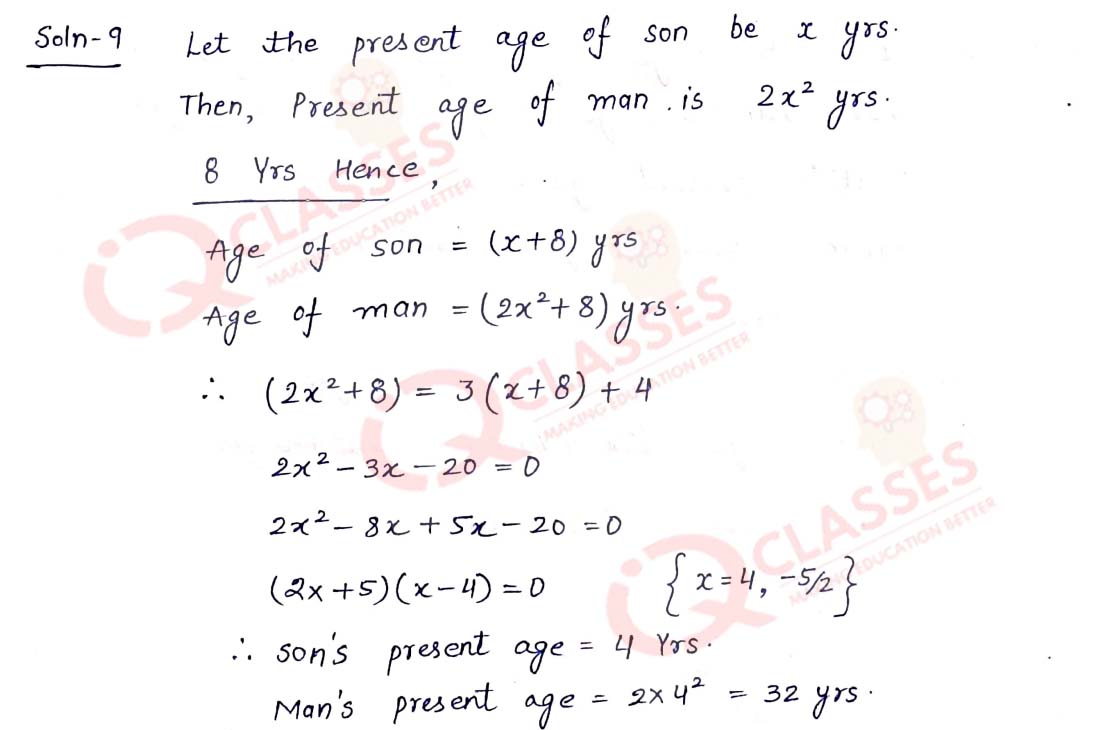
Q10 The sum of the reciprocals of Arun's ages (in years) 3 years ago and five years from now is 1/3. Find his present age.

Solution

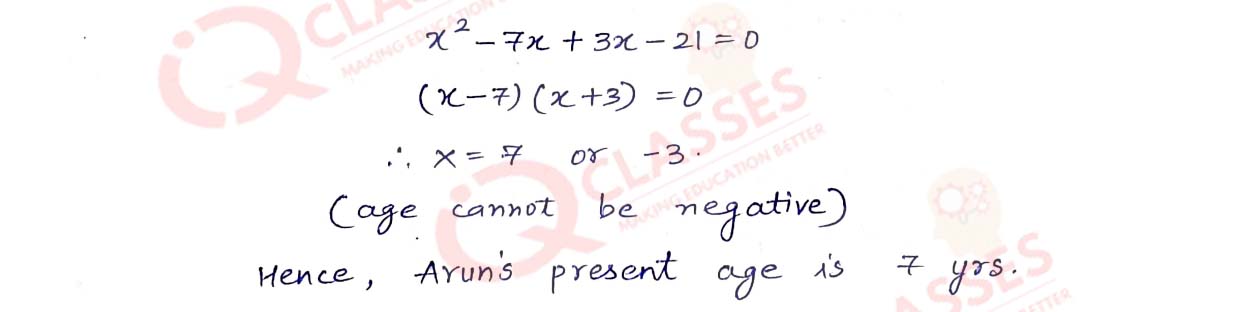
Q11 7 years ago Varun's age was five times the square of Swati's age 3 years hence, Swati's age will be two-fifth of Varun's age . Find their present ages.

Solution

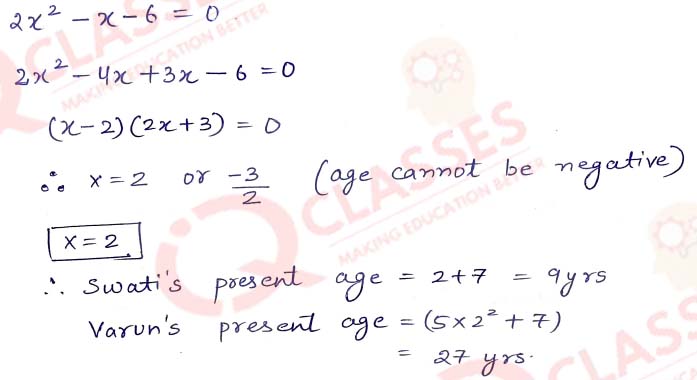
Q12 In a flight of 2800 km, an aircraft was slowed down due to bad weather. Its average speed is reduced by 100 km/hr and time of flight increased by 30 minutes. Find the original duration of the flight.

Solution

Q13 An aeroplane left 30 minutes later than its scheduled time and in order to reach its destination 1500 km away in time, it had to increase its speed by 250 km/hr from its usual speed. Determine its usual speed.

Solution

Q14 A sailor can row a boat 8 km downstream and return back to the starting point in 1 hour 40 minutes. If the speed of the stream is 2 km/hr. Find the speed of boat in still water.

Solution

Q15 A takes 6 days less than the time taken by B to finish a piece of work If both A and B together can finish it in 4 days, find the time taken by B to finish the work.

Solution

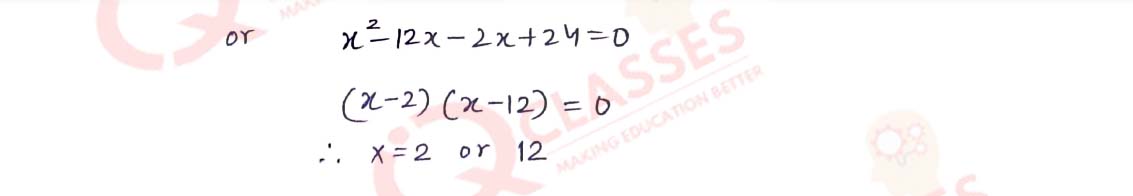
Q16 Two water taps together can fill a tank in 9
3 / 8
hours. The tap of the larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank

Solution

Q17 The hypotenuse of a right-angled triangle is 6 cm more than twice the shortest side. If the third side is 2 cm less than the hypotenuse find the sides of the triangle.

Solution

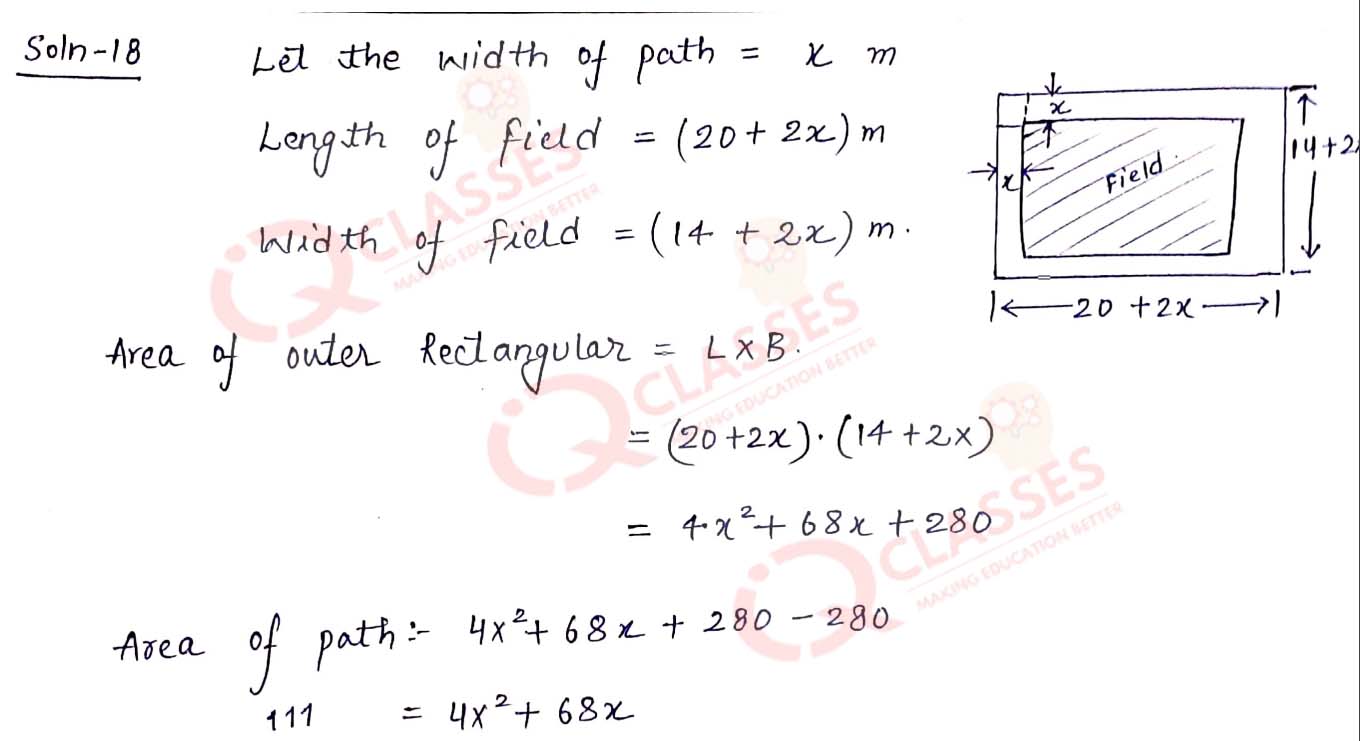
Q18 A rectangular field is 20 m long and 14 m wide. There is a path of equal width all around it, having an area of 111 sq m. Find the width of the path.

Solution

Add a comment

Reach Us

SERVICES

ACADEMIC
ON-LINE PREPARATION
FOUNDATION & CRASH COURSES

CONTACT

B-54, Krishna Bhawan, Parag Narain Road, Near Butler Palace Colony Lucknow

Contact:+918081967119

Email:info@iqclasses.in