Class 10 ICSE Maths Arithmatic Progression Important Questions

An arithmetic progression (AP) is a progression in which the difference between two consecutive terms is constant. In arithmetic progression, the first term is represented by the letter “a”, last term is represented by “l”, the common difference between two terms is represented by “d” and the number of terms is represented by the letter “n”. Thus, the standard form of the arithmetic progression is given by the formula, a, a + d, a + 2d, a + 3d, a + 4d, ….

Class 10 ICSE Arithmatic Progression Important Questions

Select Option

Board Questions
Important Questions





Arithmatic Progression Important Questions

Q1 Find the value of the middle most term(s) of the A.P.: -11, -7, -3, ..., 49

Solution

Q2 The 17th term of an A.P. is 5 more than twice its 8 th term. If the 11 th of the AP is 43, find its nth term.

Solution

Q3 The eighth term of an A.P. is half of its second term and 11th term exceeds one third of fourth term by 1. Find the 15th term.

Solution

Q4 If a, b and c are the pth, qth and rth terms respectively of an A.P., then prove that: (i)p(b- c) + q(c - a) + r(a - b) = 0 (ii) a(q - r) + b(r - p) + c(p - q) =0

Solution

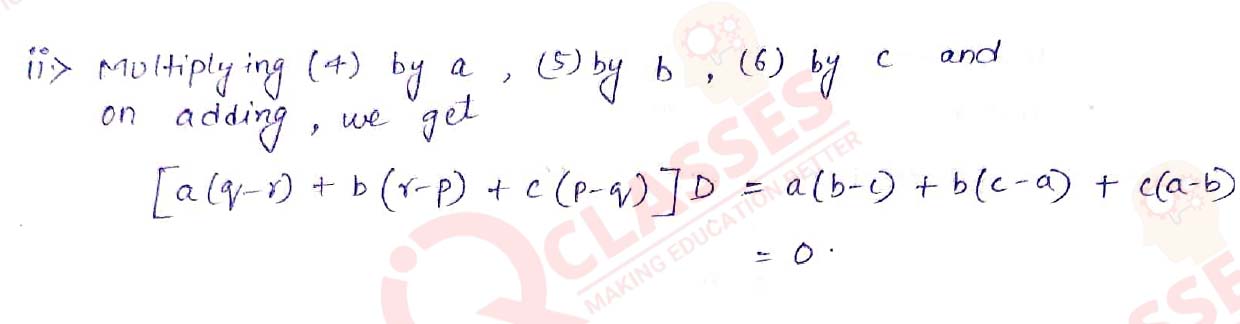
Q5 Show that the sum of (m + n)th term and (m - n)th term of an A.P. is equal to twice the nth term.

Solution

Q6 If the 9th term of an A.P. is zero, prove that its 29th term is twice its 19th term.

Solution

Q7 The sum of three numbers in A.P. is 12 and the sum of their cubes is 216. Find the numbers.

Solution

Q8 The angles of a triangle are in AP. The greatest angle is twice the least. Find all the angles of the triangle.

Solution

Q9 The digits of a positive number of three digits are m A.P. and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number.

Solution

Q10 Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?

Solution

Q11 How many terms of the A.P. -15, -13, -11, ... are needed to make the sum -55? Explain the reason for double answer.

Solution

Q12 The sum of the first five terms and the sum of first seven terms of the same AP is 167. If the sum of first ten terms of this A.P. is 235, find the sum of its first twenty terms.

Solution

Q13 Find the 60th term of the A.P. 8, 10, 12, ..., if it has a total of 60 terms and Nate. find the sum of its last 10 terms.

Solution

Q14 The sum of the third term and the seventh terms of an A.P. is 6 and their product is 8. Find the sum of first sixteen terms of the A.P.

Solution

Q15 The ratio of the 11th term to the 18th term of an A.P. is 2 : 3. Find the ratio of the 5th term to the 21st term, and also the ratio of the sum of first five terms to the sum of first 21 terms.

Solution

class10

Q16 If the ratio of the sum of first Fr terms of two A.P.'s is (7n + 1) : (4n + 27), find the ratio of their nth terms.

Solution

Q17 if Sn denotes the sum of first n terms of an A.P., prove that S12 = 3(S8 - S4)

Solution

class10

Q18 Find the sum of odd numbers between 0 and 50.

Solution

Q19 In a flower bed, there are 23 rose plants in the first row, 21 in the second row, 19 in the third row, and so on. There are 5 rose plants in the last row. How many rose plants are there in the flower bed?

Solution

Q20 Find the middle term of the sequence formed by all three digit numbers Which leave a remainder 3 when divided by 4. All find the sum of all numbers on both sides of the middle term

Solution

Add a comment

Reach Us

SERVICES

  • ACADEMIC
  • ON-LINE PREPARATION
  • FOUNDATION & CRASH COURSES

CONTACT

B-54, Krishna Bhawan, Parag Narain Road, Near Butler Palace Colony Lucknow
Contact:+918081967119