Class 10 ICSE Maths Equation Of Line Important Questions
The general equation of a line in two variables of the first degree is represented as Ax + By +C = 0, A, B ≠ 0 where A, B and C are constants which belong to real numbers. When we represent the equation geometrically, we always get a straight line.s
Class 10 ICSE Equation Of Line Important Questions
Equation Of Line Important Questions
Q.1
The line 
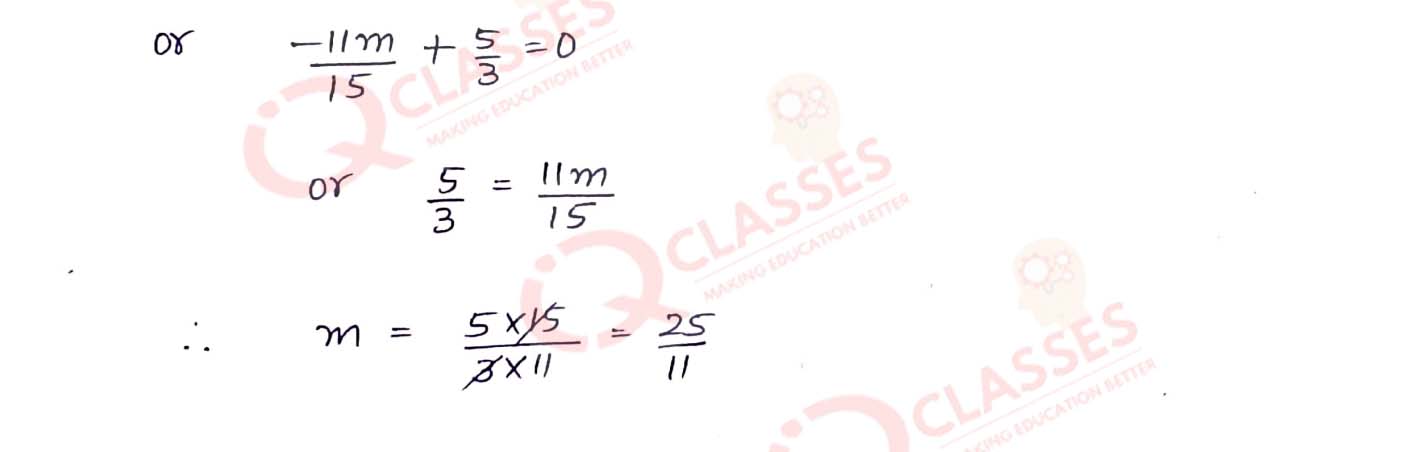
3x
/
5
-
2y
/
3
+ 1 = 0 contains the
the point (m, 2m - 1); calculate the value of m.
Solution

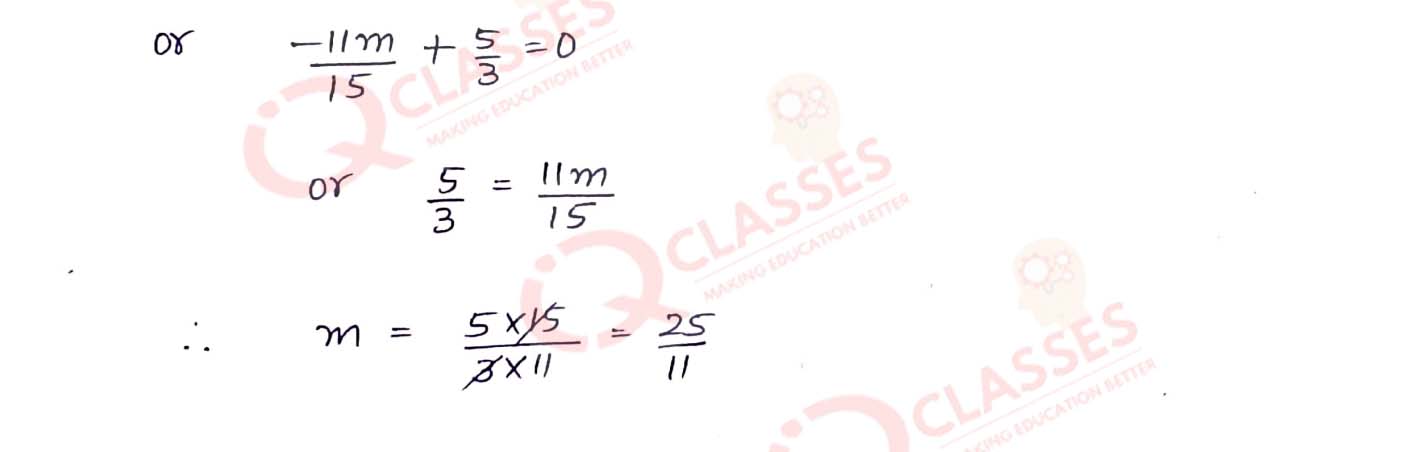
Q2
The line segment joining A(2, 1) and B(5, -8) is trisected at the points P and Q. If P is closer to
point A and lies on the line 2x - y + k = 0, find the value of k
Solution




Q3
Find the slope of the line passing through the points A (-2, 3) and B (2, 7) Also find:
(i) the inclination of the line AB,
(ii) slope of the line parallel to AB,
(iii) slope of the line perpendicular to AB. Solution

(i) the inclination of the line AB,
(ii) slope of the line parallel to AB,
(iii) slope of the line perpendicular to AB. Solution


Q4
Given the points A (2, 3), B (-5, 0) and C (-2, a) are collinear. Find 'a'.
Solution


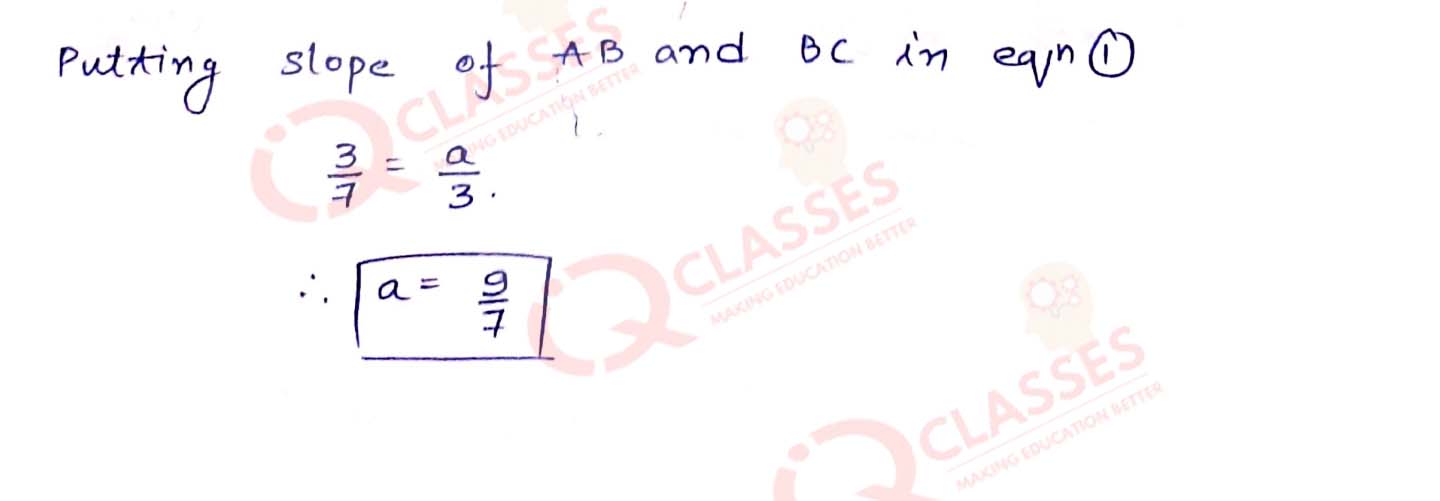


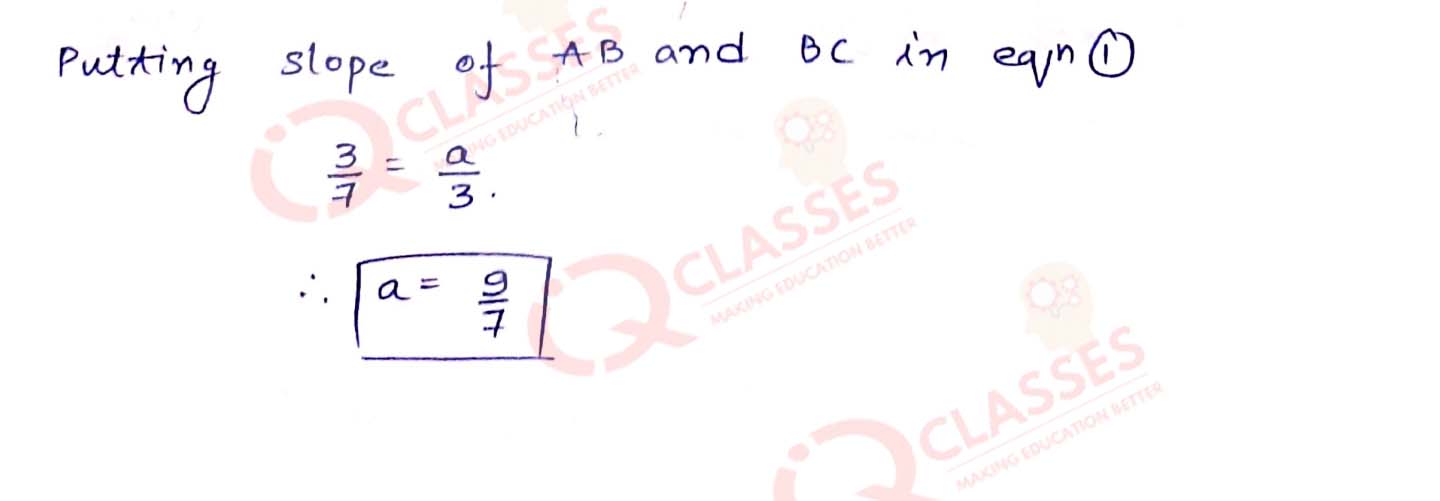
Q5
Find the equation of a line :
(i) whose inclination is 45° and y-intercept is 5.
(ii) with inclination = 60° and passing through (-2, 5).
(iii) passing through the points (-3, 1) and (1, 5). Solution

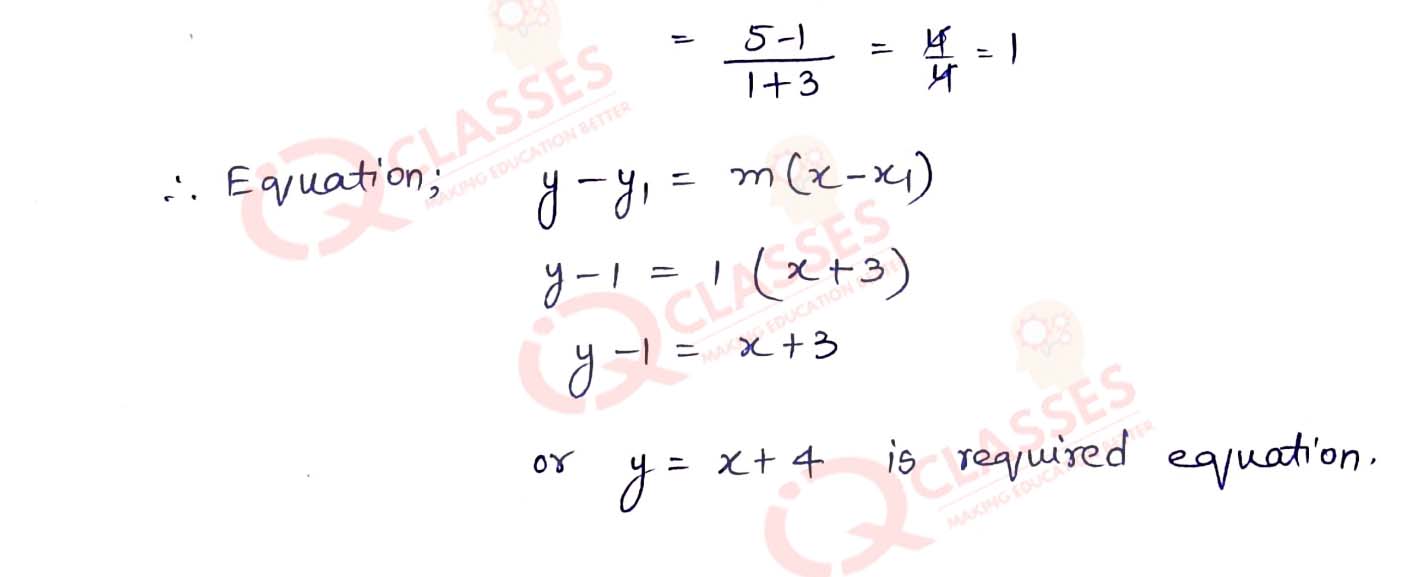
(i) whose inclination is 45° and y-intercept is 5.
(ii) with inclination = 60° and passing through (-2, 5).
(iii) passing through the points (-3, 1) and (1, 5). Solution


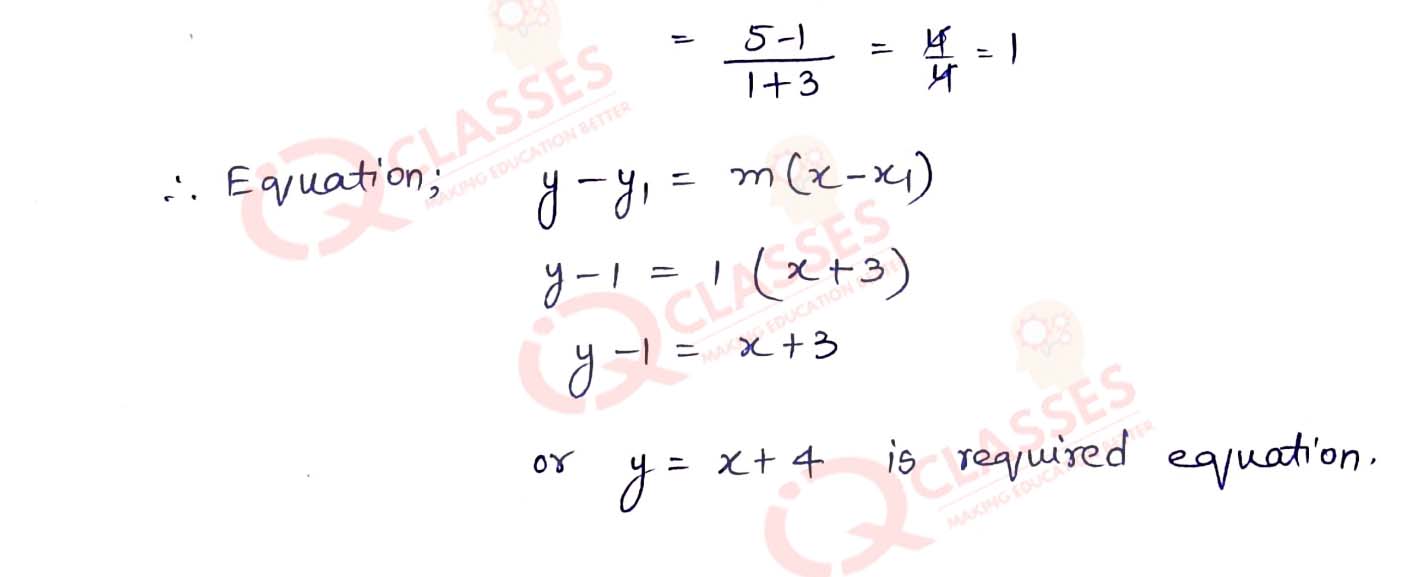
Q6
Find the equation of the line whose x-intercept is 8 and y-intercept is -12.
Solution




Q7
The equation of a line is 3x - 4y + 12 - 0. It meets the x-axis at point A and the y-axis at point
B. Find :
(i) the co-ordinates of points A and B;
(ii) the length of intercept AB, cut by the line within the co-ordinate axes. Solution
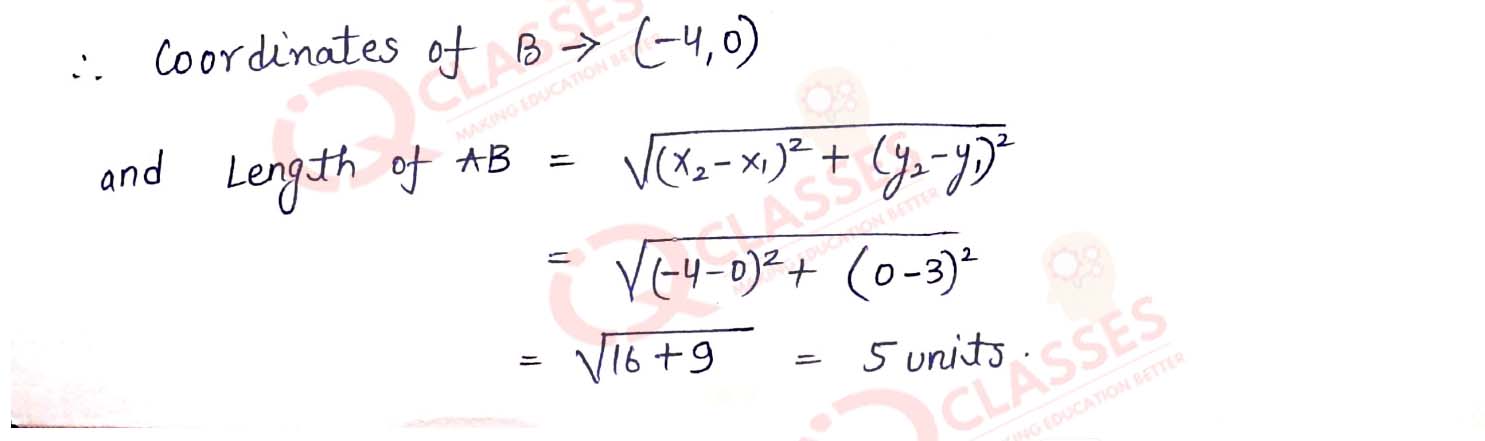
(i) the co-ordinates of points A and B;
(ii) the length of intercept AB, cut by the line within the co-ordinate axes. Solution

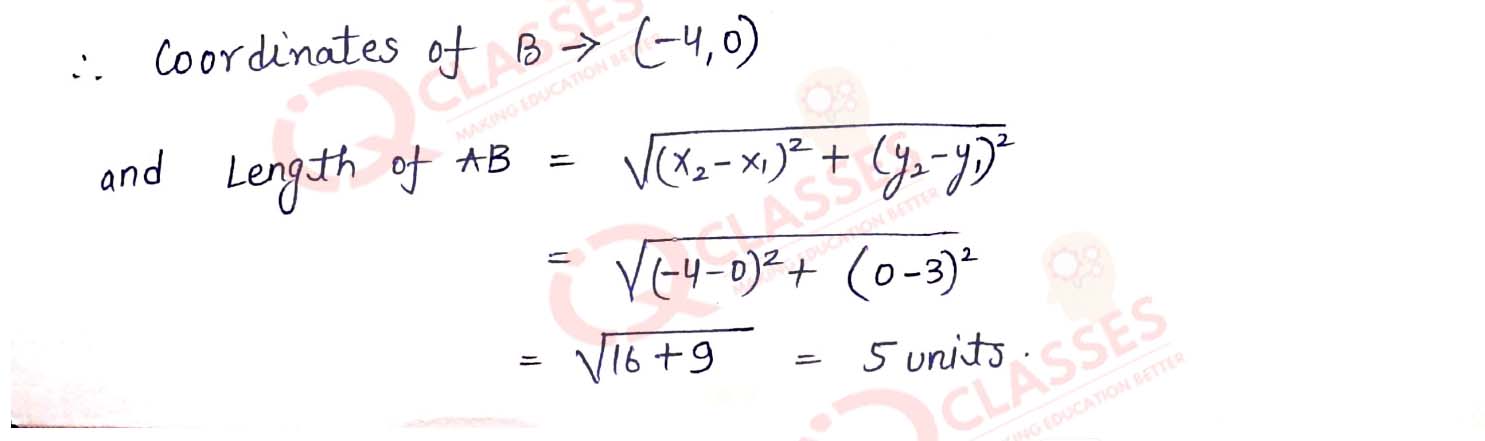
Q8
Write down the equation of the line whose gradient is 3/2 and which passes through P, where P
divides the line segment joining A (-2, 6) and B (3. -4) the ratio 2 : 3.
Solution


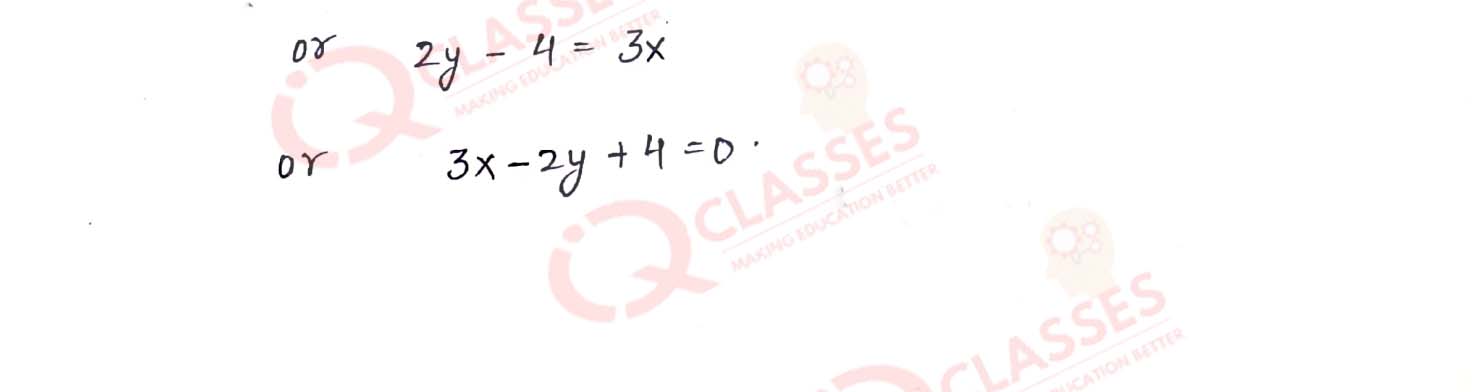


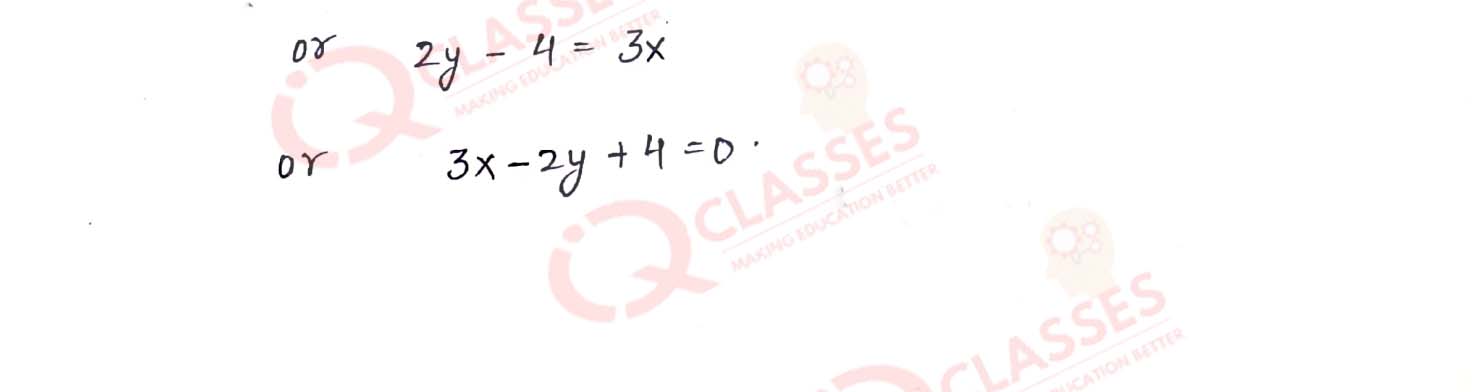
Q9
A straight line passes through the point P(3, 2). It meets the x-axis at point A
and the y-axis at point B. If 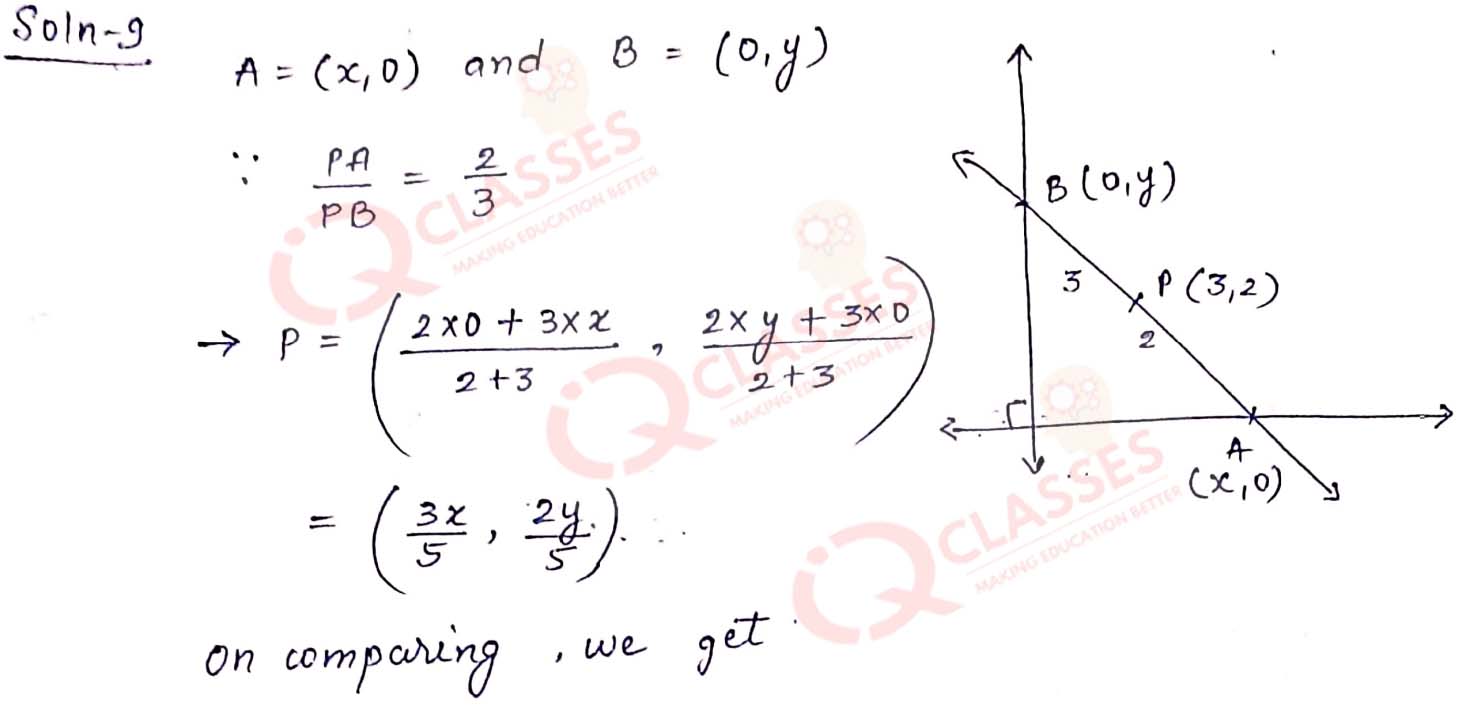


PA
/
PB
= -3, find the equation of the line that passes through the point P and is perpendicular to
line AB.
Solution



Q10
Find the equations of the lines passing through point (-2, 0) and equally inclined to the
co-ordinate axes.
Solution




Q11
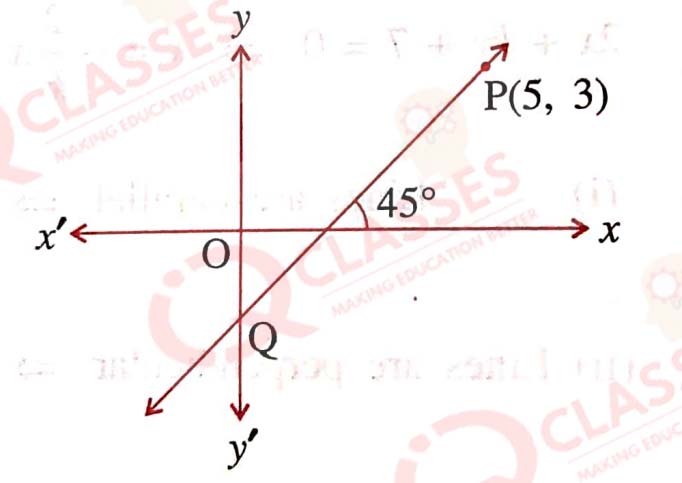
The line through P(5, 3) intersects y-axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the co-ordinates of Q.
 Solution
Solution
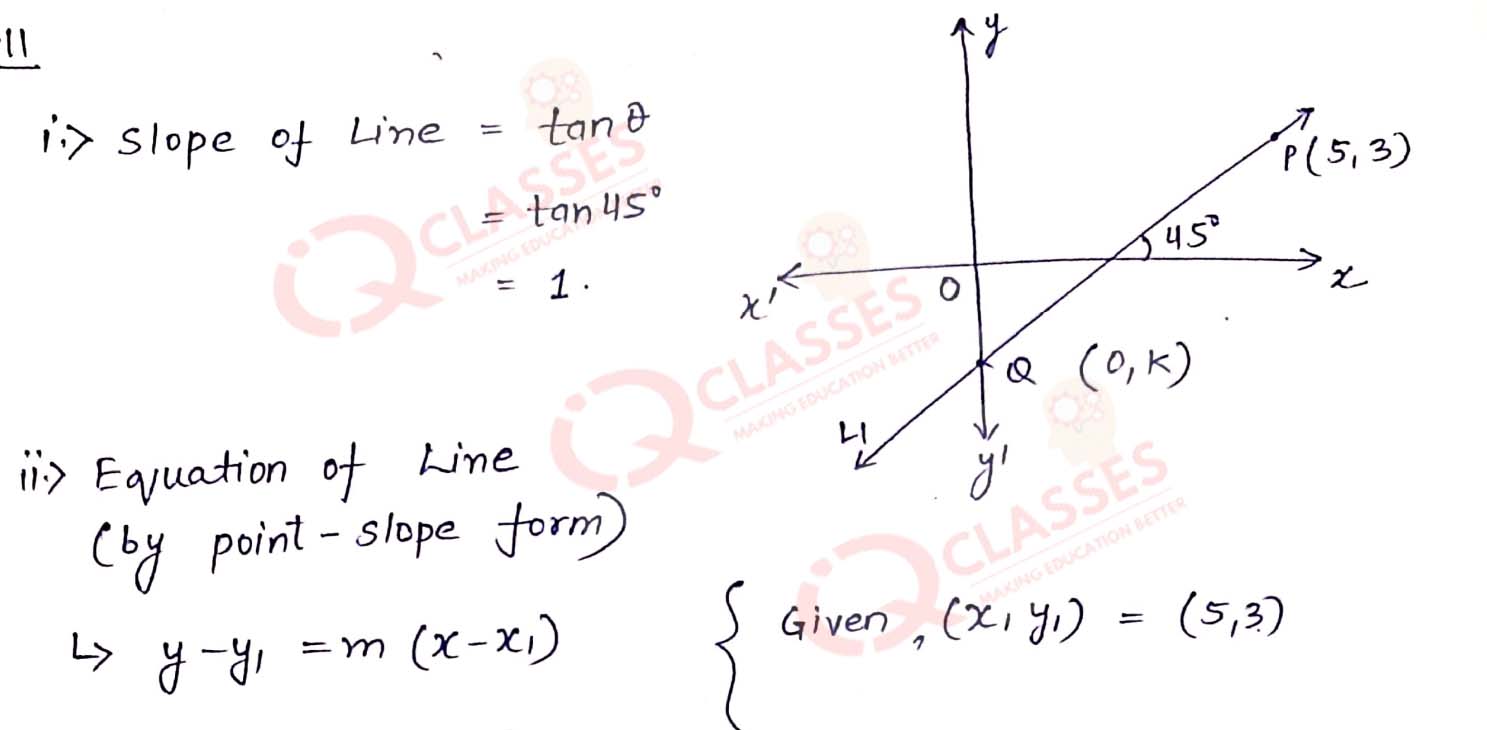

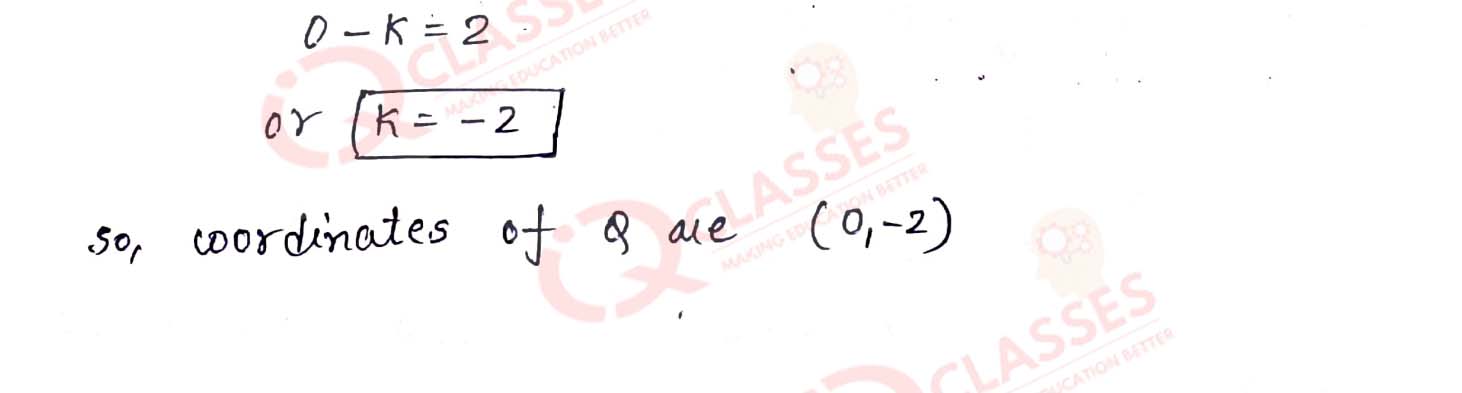
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the co-ordinates of Q.
 Solution
Solution


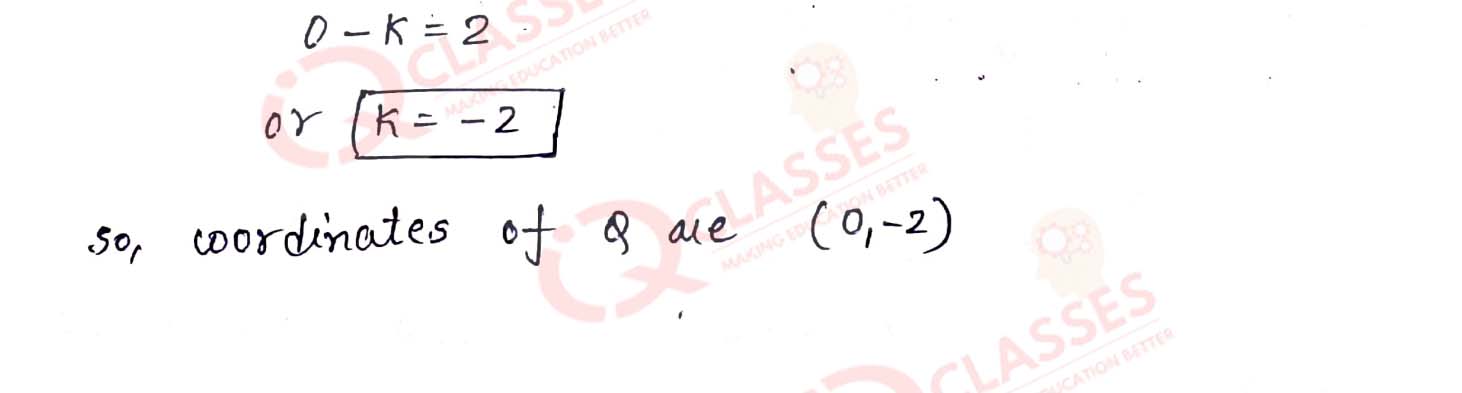
Q12
Given two straight lines 3x - 2y = 5 and 2x + ky + 7 = 0. Find the value of k at which the given
lines are :
(i) parallel to each other.
(ii) perpendicular to each other. Solution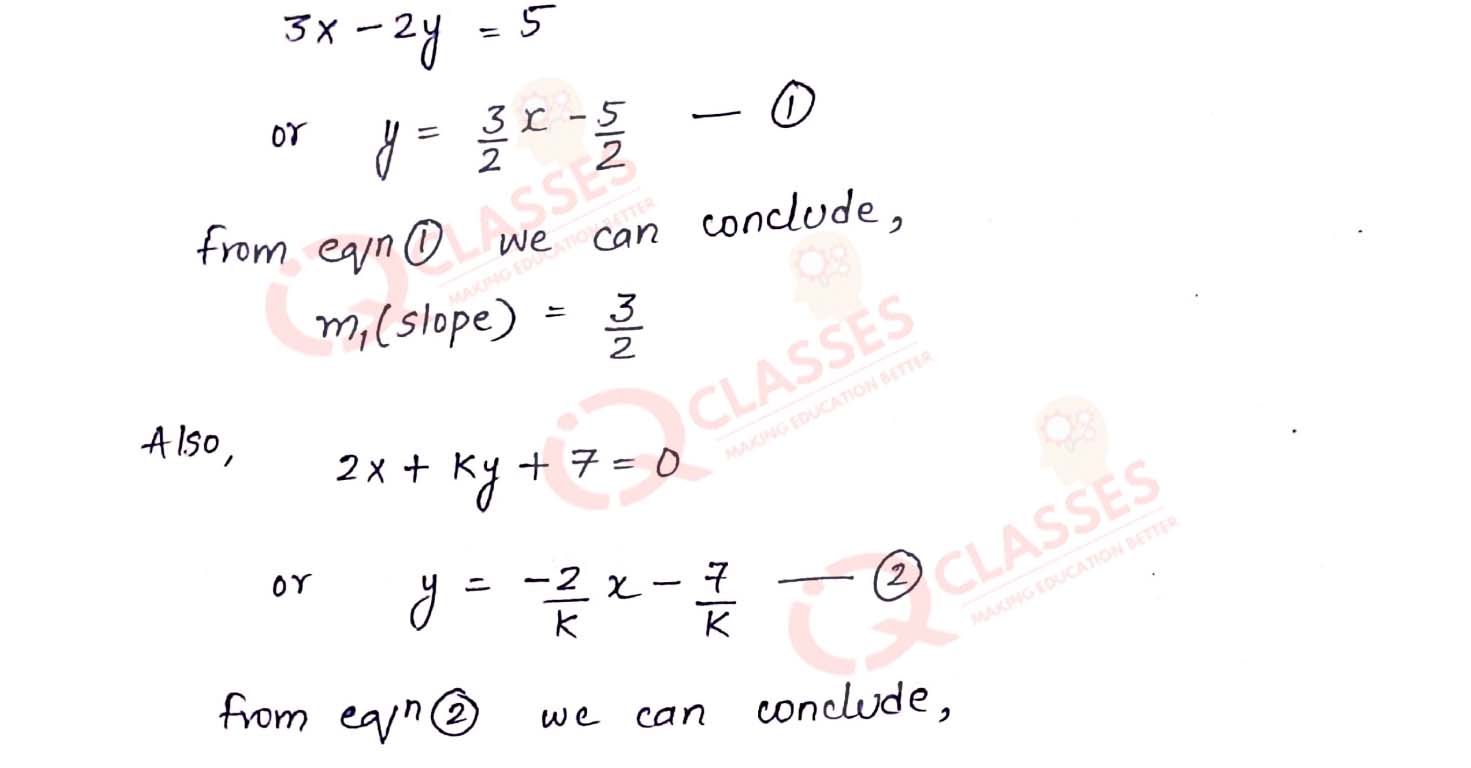

(i) parallel to each other.
(ii) perpendicular to each other. Solution
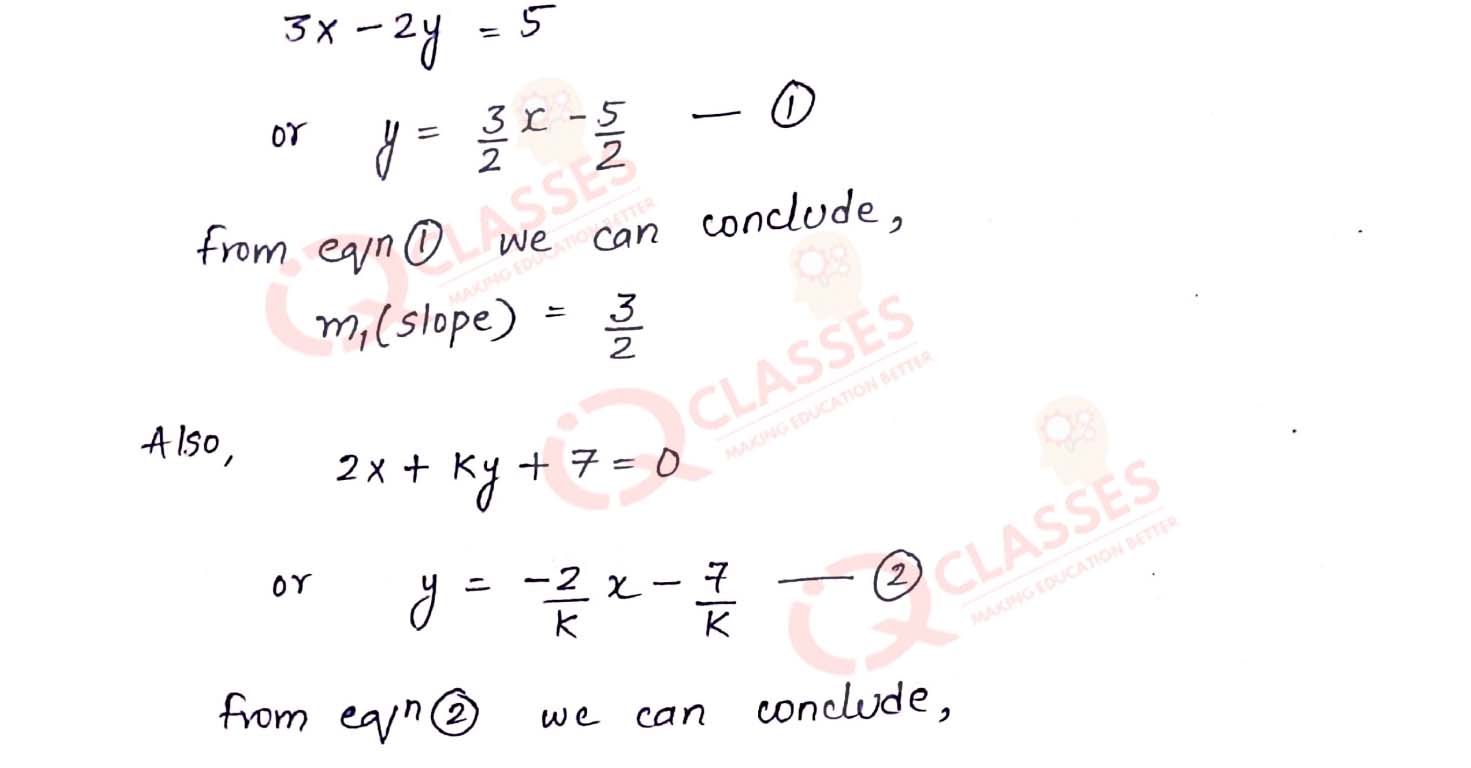

Q13
Find the equation of the line which passes through the point (-2, 3) and is perpendicular to the
line 2x + 3y + 4 = 0
Solution
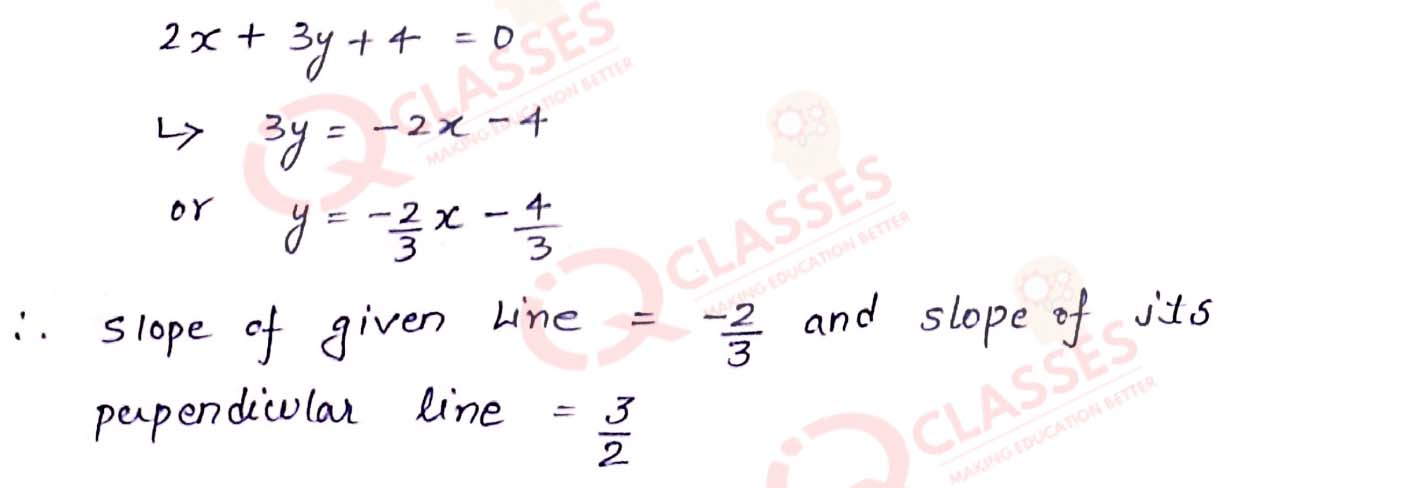

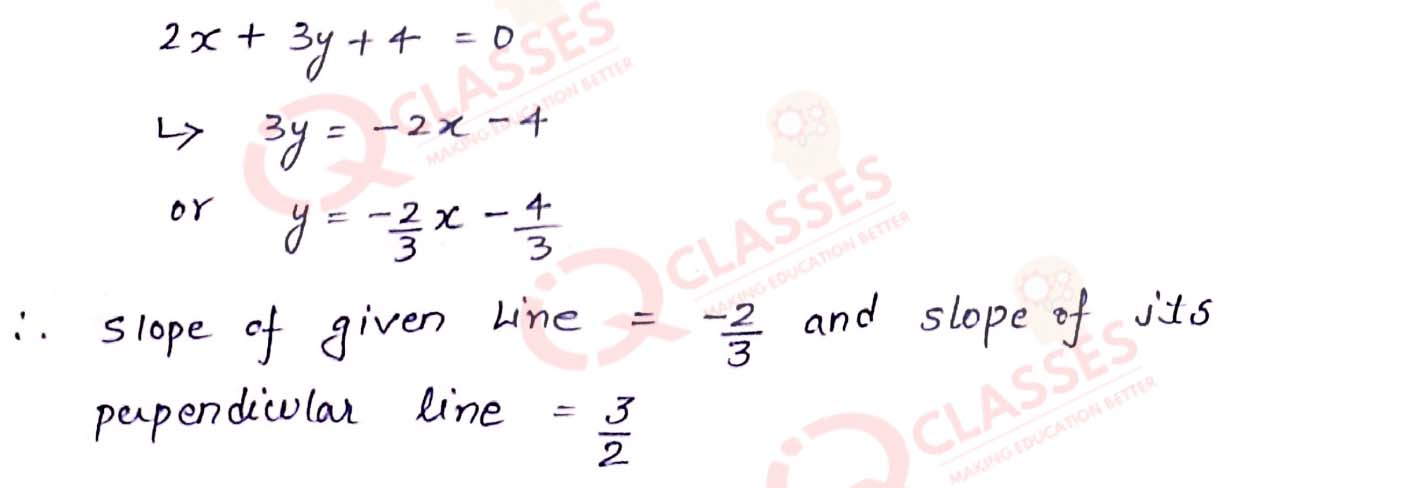

Q14
ABCD is a rhombus. The co-ordinates of A and C are (3, 6) and (-1, 2) respectively. Find the
equation of BD.
Solution


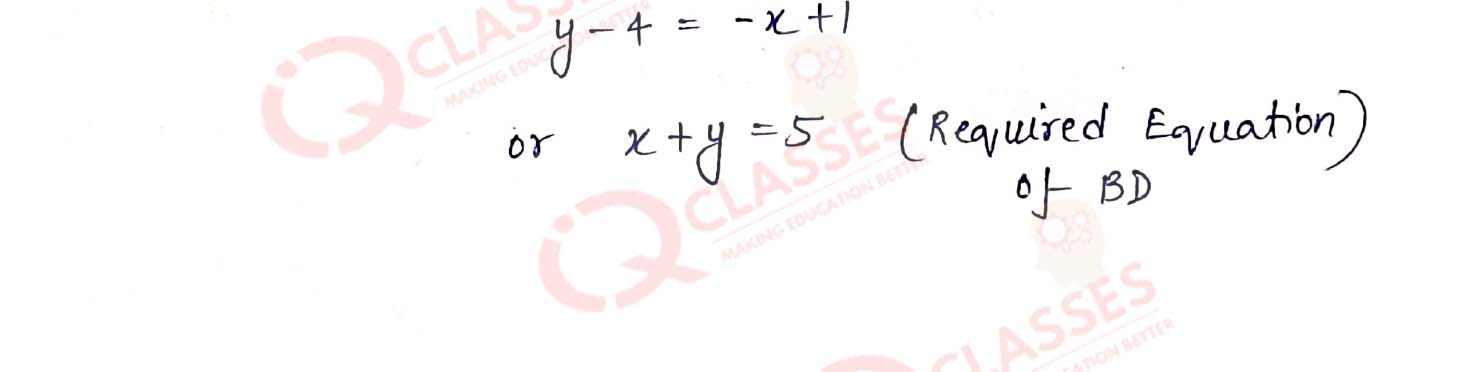


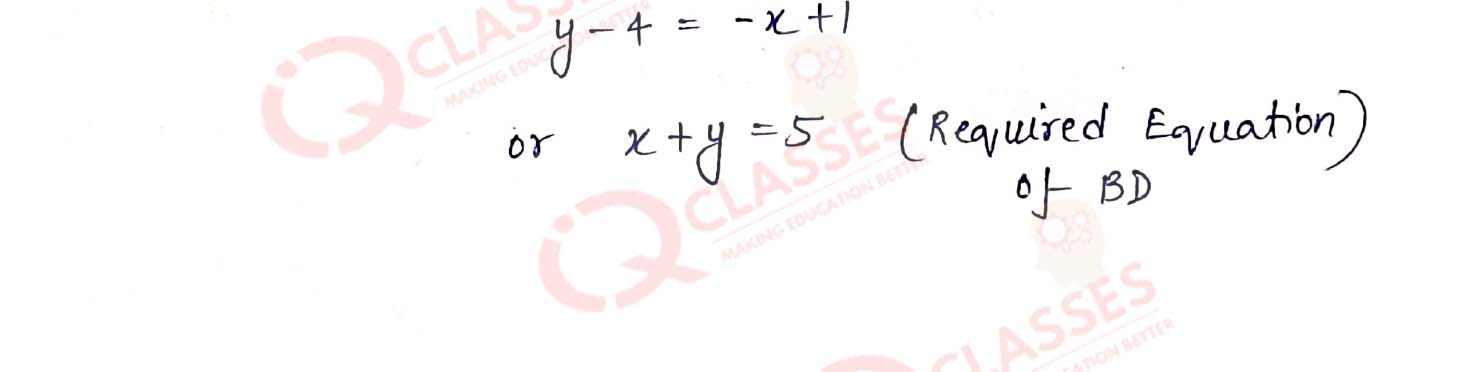
Q15
Find the equation of the perpendicular bisector of the line segment obtained on joining the points
(6, -3) and (0, 3).
Solution







Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment