Class 10 ICSE Maths Quadratic Equations Important Questions
When we equate a quadratic polynomial to a constant, we get a quadratic equation.
Any equation of the form p(x) = k, where p(x) is a polynomial of degree 2 and c is a constant, is a quadratic
equation.
The standard form of a quadratic equation is ax2+bx+c=0, where a,b and c are real numbers and a≠0.
‘a’ is the coefficient of x2. It is called the quadratic coefficient. ‘b’ is the coefficient of x. It
is called the linear coefficient. ‘c’ is the constant term.
Class 10 ICSE Quadratic Equations Important Questions
Quadratic Equations Important Questions
Q.1
Check whether the following are quadratic equations:
(i)(x — 2)2 + 1 = 2x — 3
(ii) x(x + 1) + 8 = (x + 2) (x - 2)
(iii) x(2x + 3) = x2 + 1
(iv) (x + 2)3 = x3 — 4
Solution




Q2 Find the roots of the quadratic equation : 3x2 - 2√6 x + 2 = 0
Solution

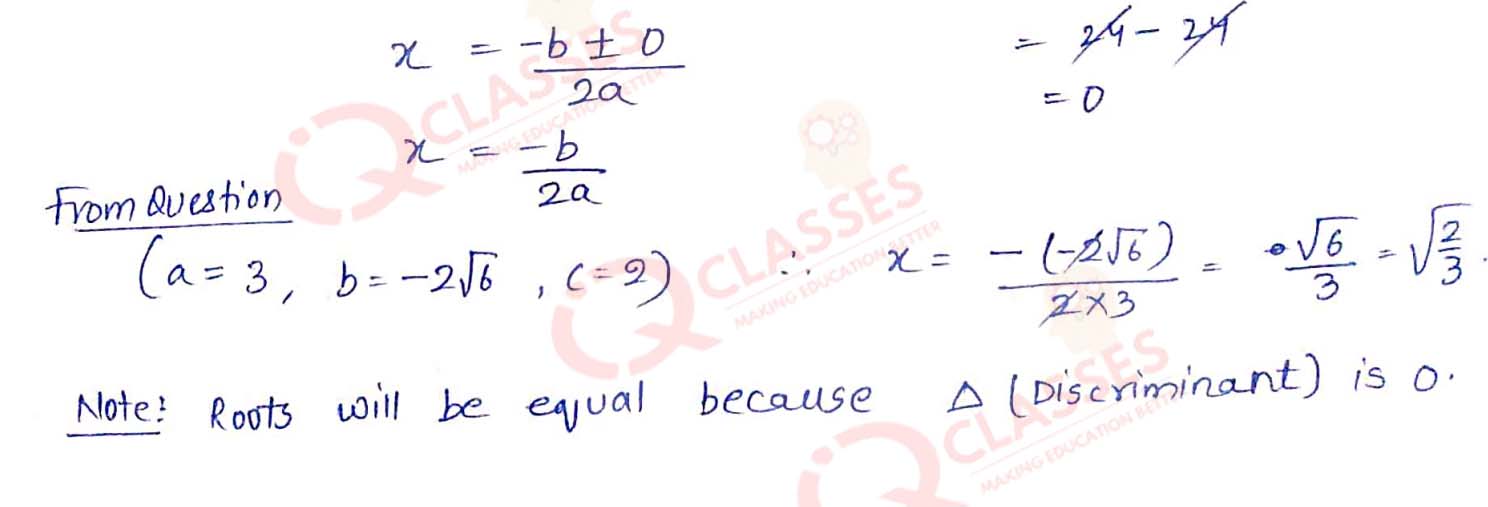
Q3 Find the roots of the equation 5x2 — 6x— 2 = 0 by the method of completing. square.
Solution

Q4 Find two consecutive odd positive integers sum of whose square is 290.
Solution


Q5
Find the roots of the following:
(i) x + 1/x = 3, x ≠ 0
(ii) 1/x - 1/x-2 = 3 , x ≠ 0,2
Solution

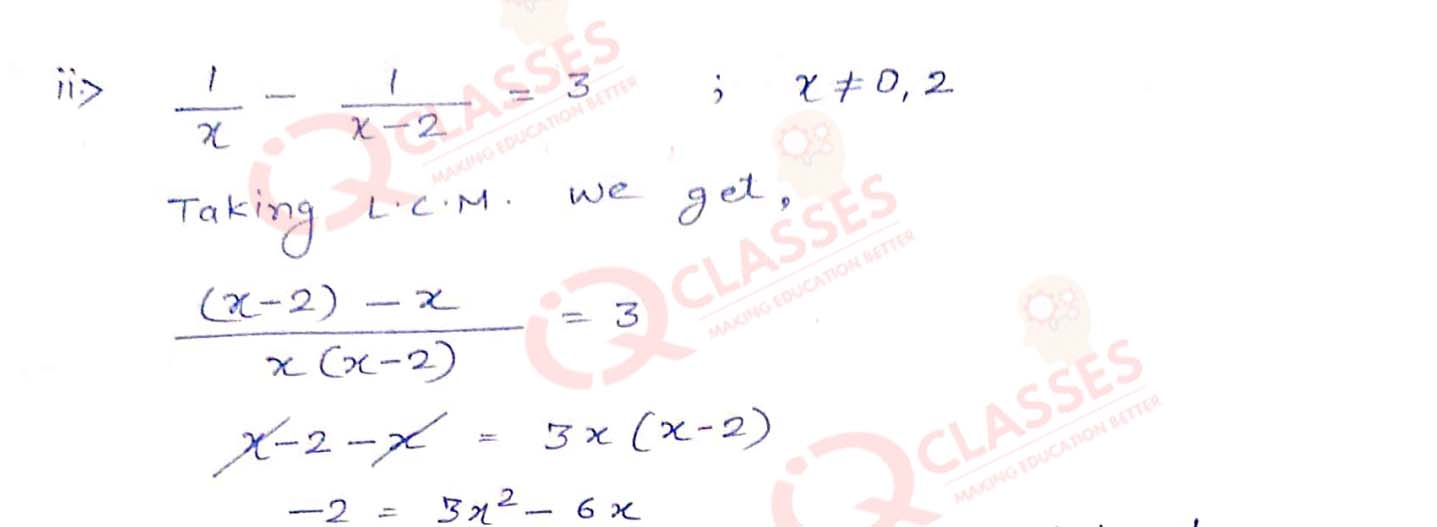

Q6
Solve the following equationand give you answer correct to 3 significant figure:
5x2-3x -4 = 0
Solution

Q7
Solve for x using the quadratic formula write your answer correct to 2 significant figures
(x-1)2 - 3x + 4 = 0
Solution


Q8
Solve the quadratic equation x2 -3(x+3)=0; give your answer correct to 2 significant
figures
Solution


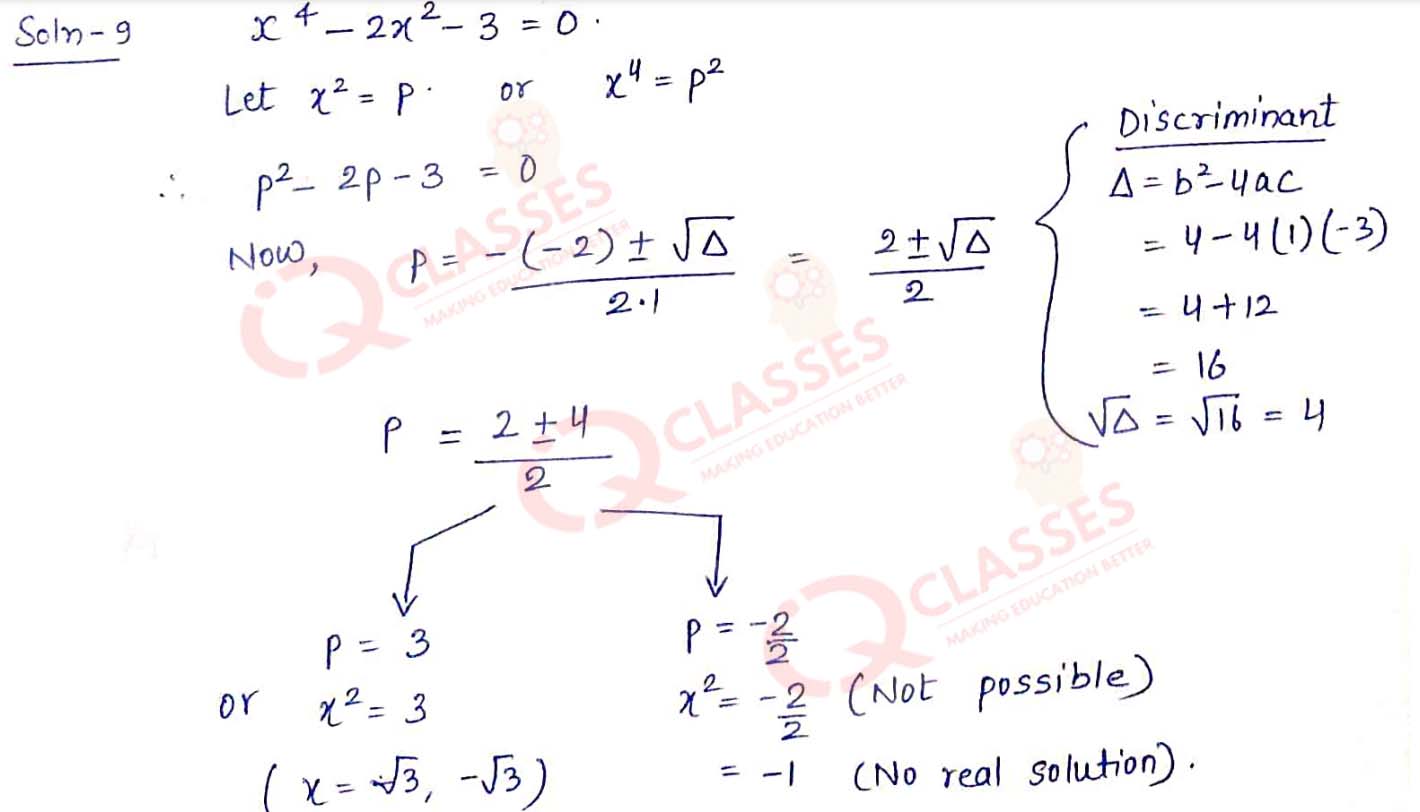
Q9 x4-2x2-3=0
Solution
Q10
9(x2 + 1/x2) - 9(x+1/x) - 52 = 0
Solution


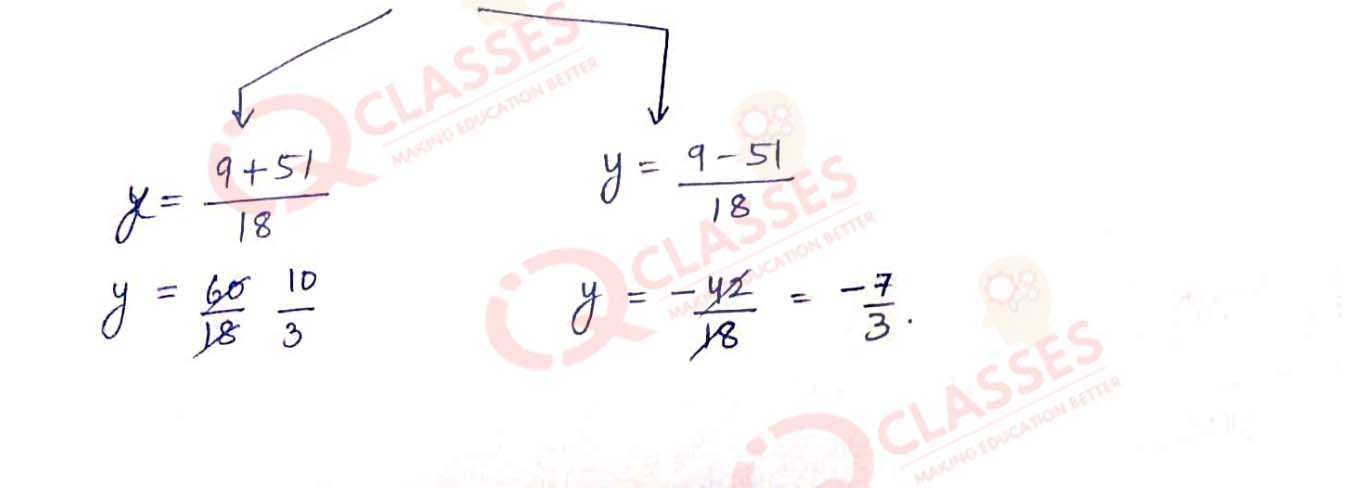


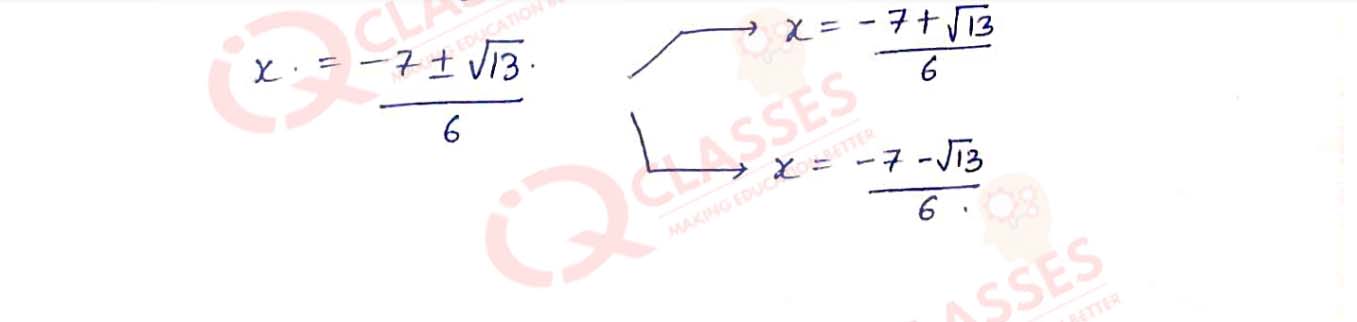
Solution






Q11 (x2 + 1/x2) - 3(x - 1/x) -2 = 0
Solution

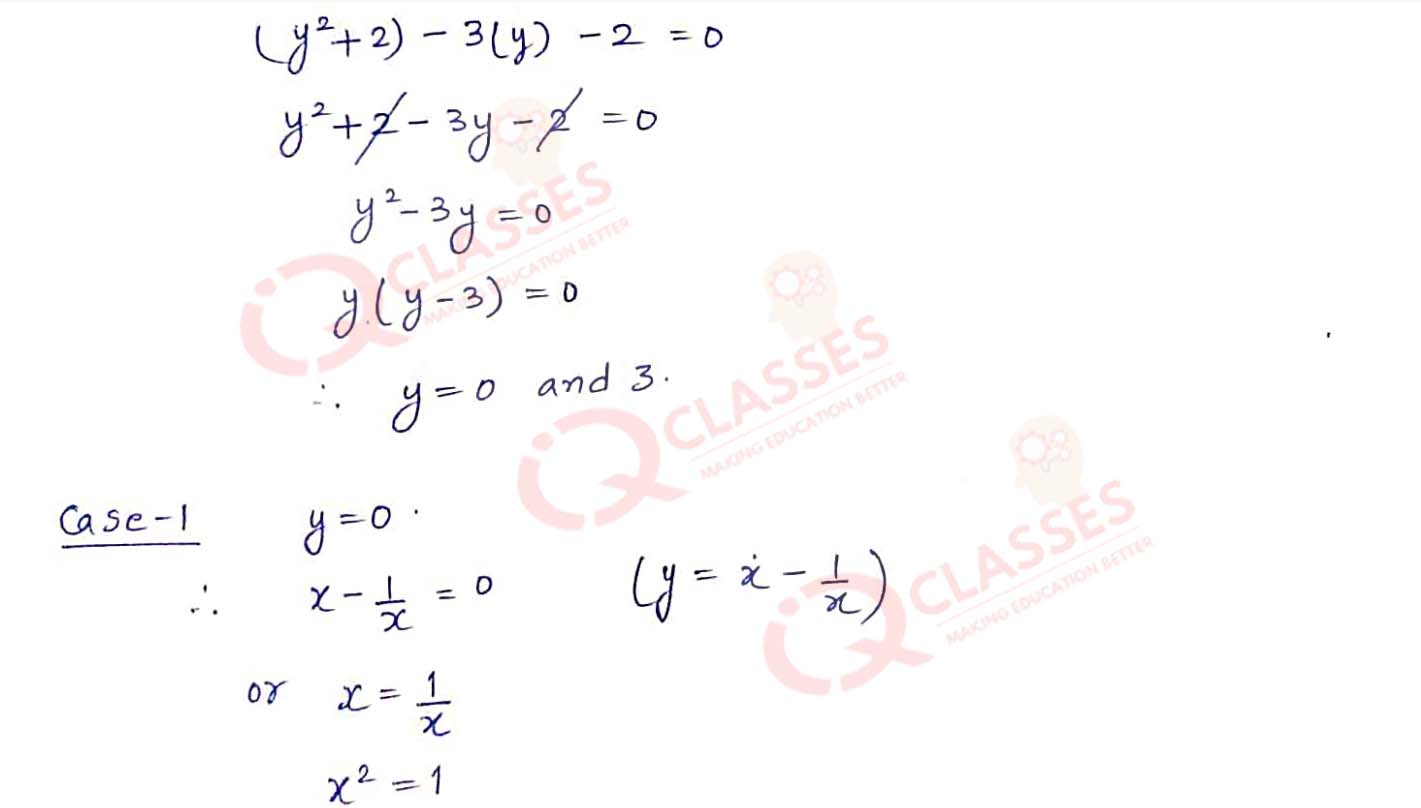
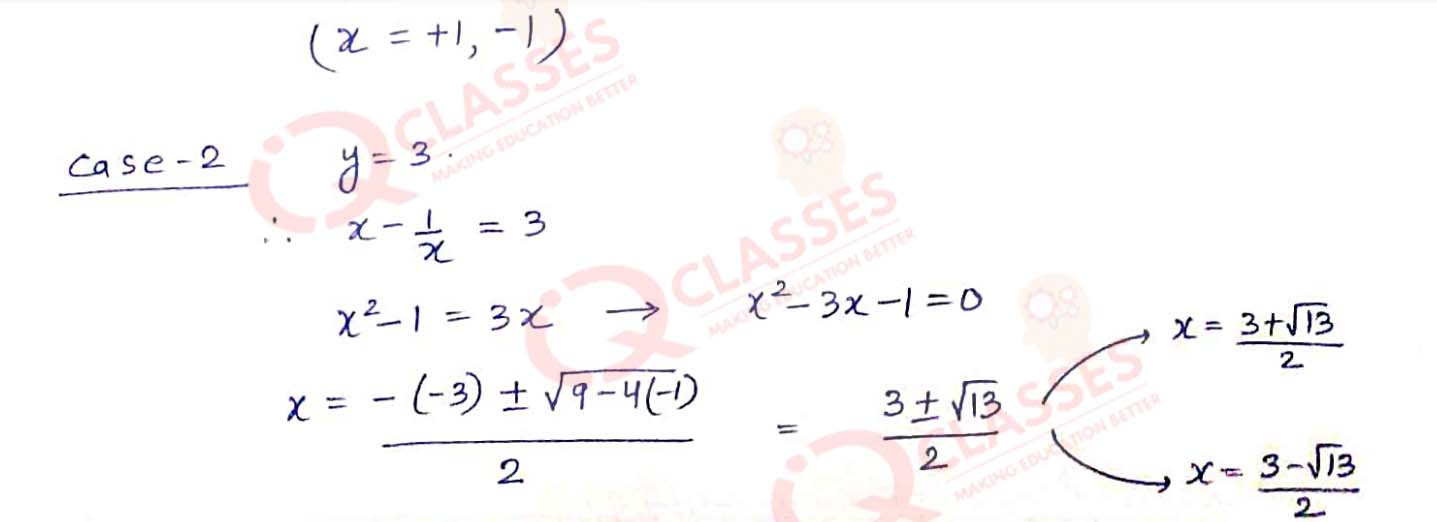
Q12
Solve for x : 4(x - 1/x)2 + 8(x + 1/x)=29 , x≠ 0.
Solution
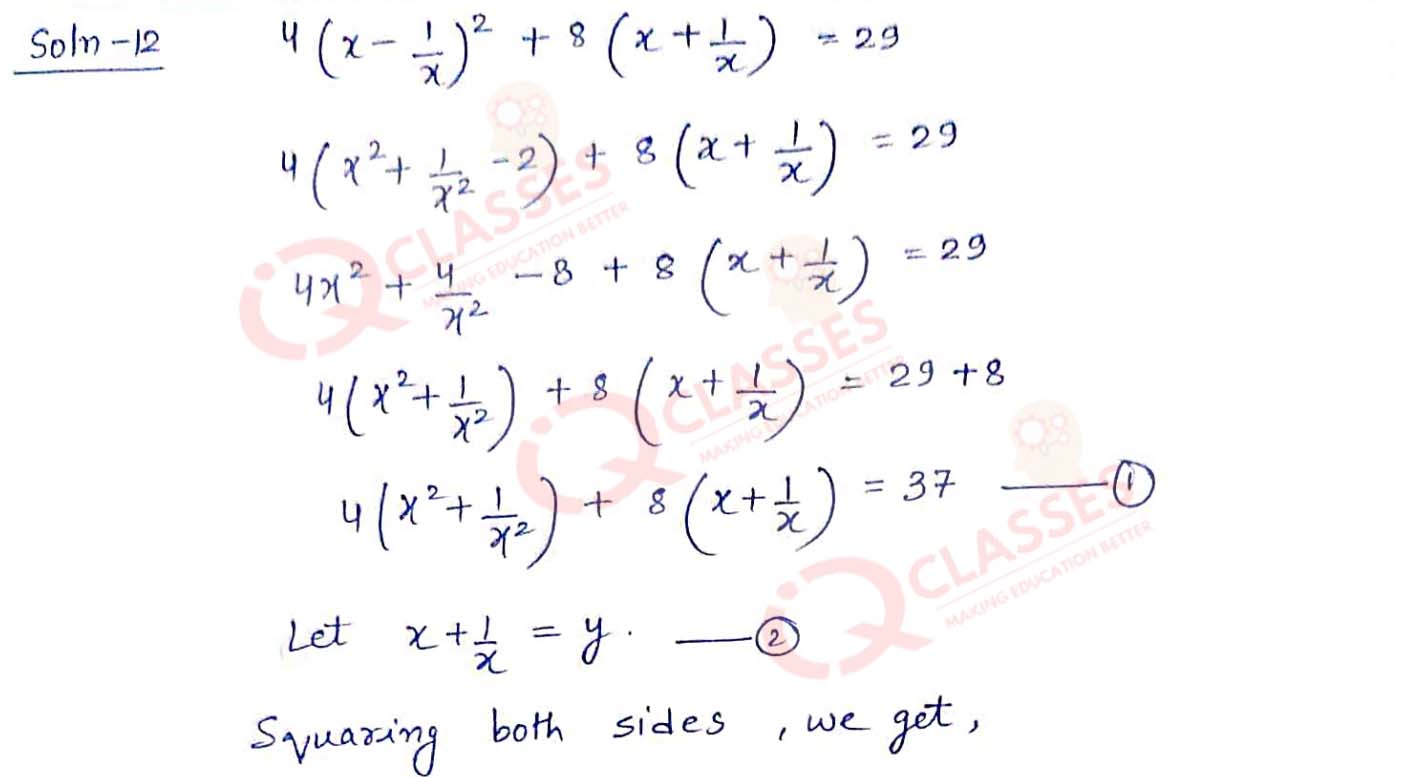





Q13
√(x/(1-x)) + √((1-x)/x) = 2(1/6), x≠ 0 and x≠ 1
Solution



Q14
If x = 2 and x = 3 are roots of the equation 3x2-2mx+2n=0; find the value of m and n
Solution


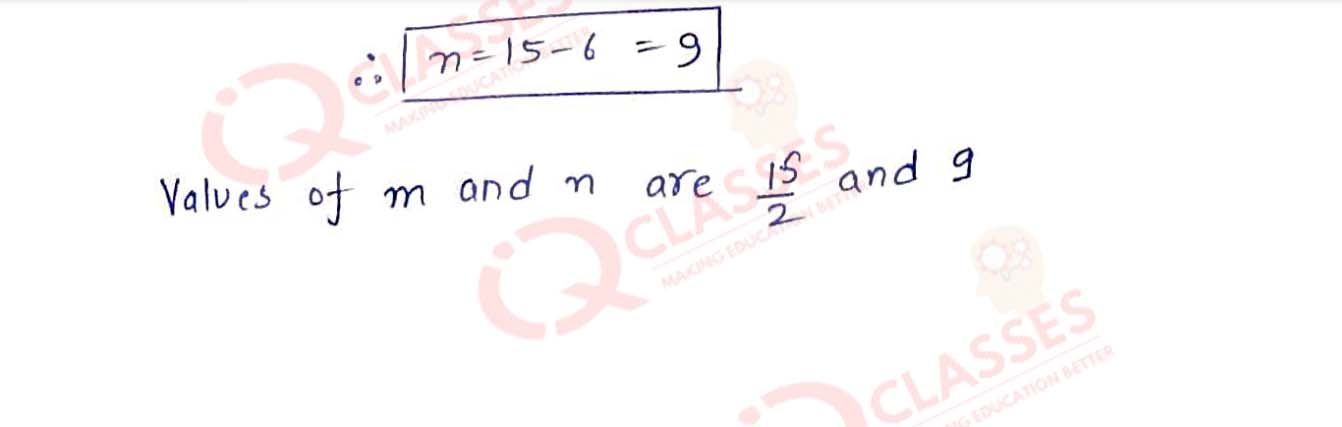
Q15 Find the value of 'K'for which x = 3 is a solution of the quadratic equation (K+2)x2-Kx + 6 ,hence find the other root of the equation
Solution

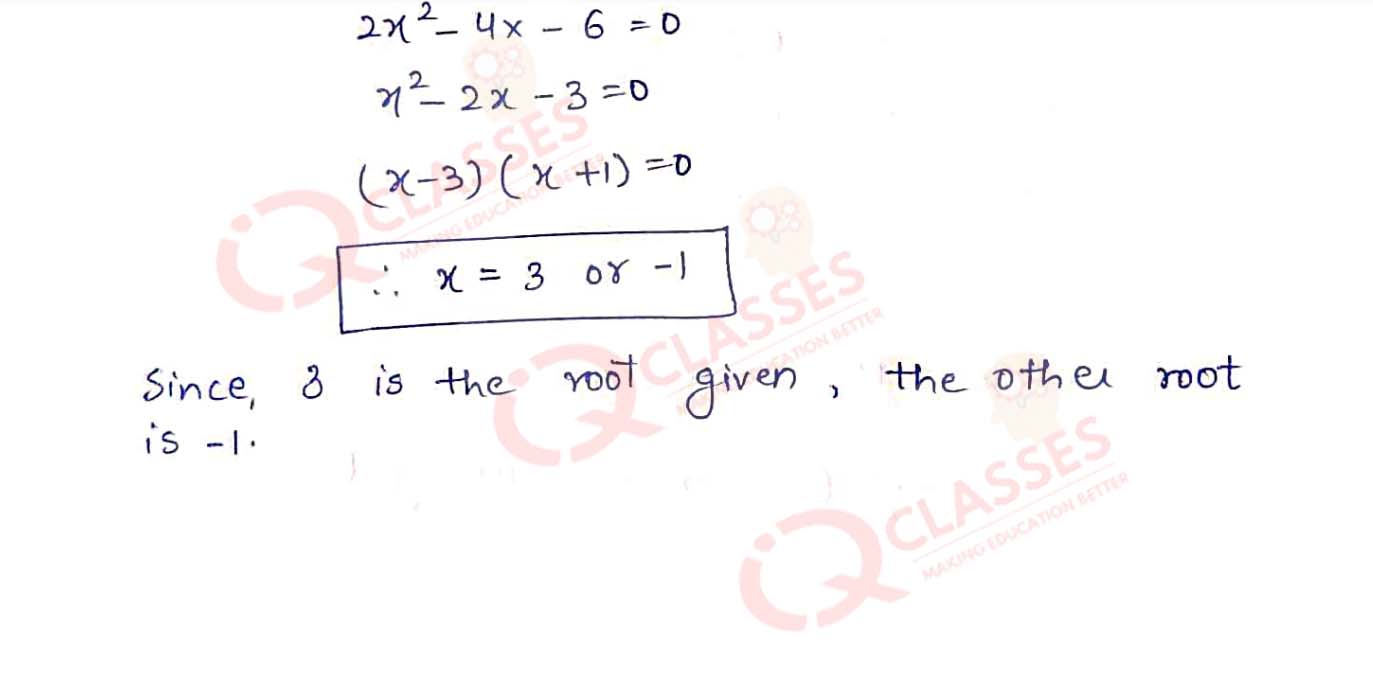
Quadratic Equation(Word Problems)
Q1 Five times a certain whole number is equal to three less than twice the square of the number. Find the number.
Solution

Q2 For the same amount of work, A takes 6 hours less than B. If together they complete the work in 13 hours 20 minutes; find how much time will B alone take to complete the work ?
Solution


Q3 Divide 15 into two parts such that the sum of their reciprocals is 3/10
Solution

Q4 A can do a piece of work in 'x' days and B can do the same work in (x + 16) days. If both working together can do it in 15 days; calculate 'x'
Solution

Q5 One pipe can fill a cistern in 3 hours less than the other. The two pipes together can fill the cistern in 6 hours 40 minutes. Find the time that each pipe will take to fill the cistern.
Solution


Q6 The hypotenuse of a right-angled triangle exceeds one side by 1 cm and the other side by 18 cm; find the lengths of the sides of the triangle.
Solution


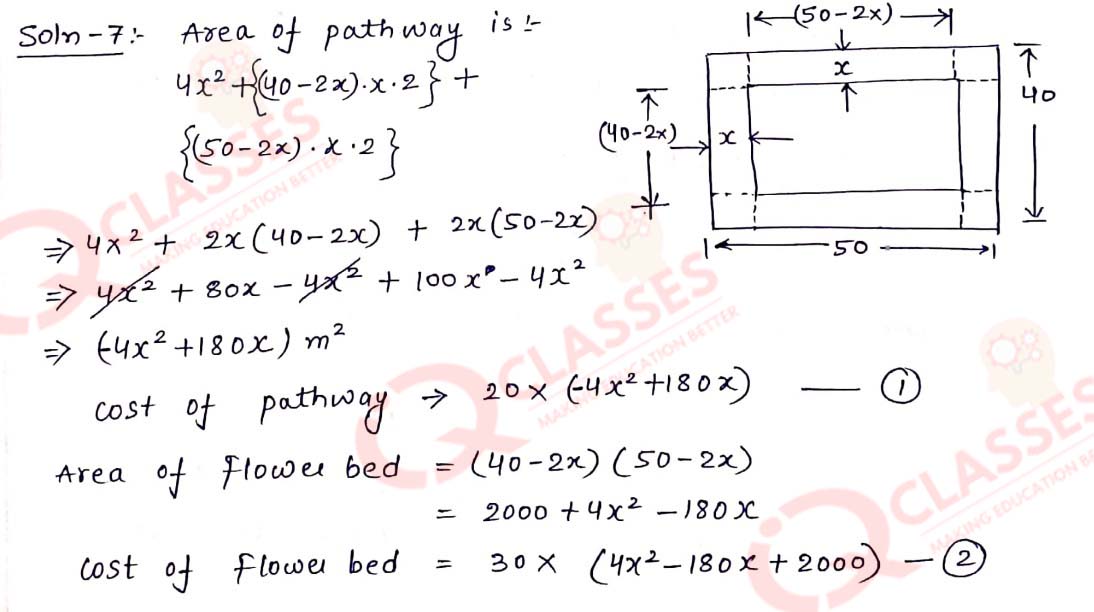
Q7 The dimensions of a rectangular field are 50 m by 40 m. A flower bed is prepared inside this field leaving a gravel path of uniform width all around the flower bed. The total cost of laying the flower bed and gravelling the path at Rs30 and Rs20 per square metre, respectively, is Rs52,000. Find the width of the gravel path.
Solution

Q8 By increasing the speed of a car by 10 km/hr, the time of journey for a distance of 72 km is reduced by 36 minutes. Find the original speed of the car.
Solution

Q9 The area of a big rectangular room is 300 m2. If the length were decreased by 5 m and the breadth increased by 5 m; the area would be unaltered. Find the length of the room.
Solution


Q10
Car A travels x km for every litre of petrol, while car B travels (x + 5) km for every litre of
petrol.
- Write down the number of litres of petrol used by car A and car B in covering a distance of
400 km.
- If car A uses 4 litres of petrol more than car B in covering the 400 km, write down an
equation in x and solve it to determine the number of litres of petrol used by car B for the
journey.
Solution


Q11 By selling an article for Rs24, a trader loses as much percent as the cost price of the article. Calculate the cost price.
Solution

Q12 The sum S of first n natural numbers is given by the relation : S = 1/2 n(n + 1). Find n, if the sum is 276.
Solution


Q13 A two-digit number is such that the product of its digits is 6. When 9 is added to this number; the digits interchange their places. Find the number.
Solution

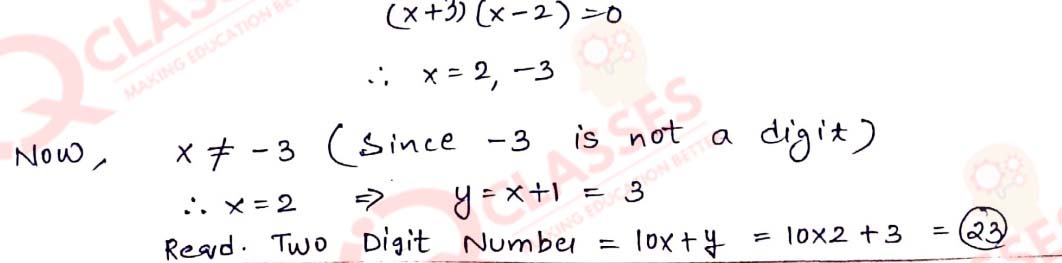
Q14
Five years ago, a woman's age was the square of her son's age. Ten years hence her age will be twice
that of her son's age. Find:
- the age of the son five years ago.
- the present age of the woman.
Solution


Q15 A motor-boat, whose speed is 9 km/h in still water, goes 12 km downstream and comes back in a total time of 3 hours. Find the speed of the stream.
Solution


Q16 Some students planned a picnic. The budget for the food was Rs480. As eight of them failed to join the party, the cost of the food for each member increased by Rs10. Find, how many students went for the picnic ?
Solution


Q17 Rs250 is divided equally among a certain number of children. If there were 25 children more, each would have received 50 paise less. Find the number of children.
Solution

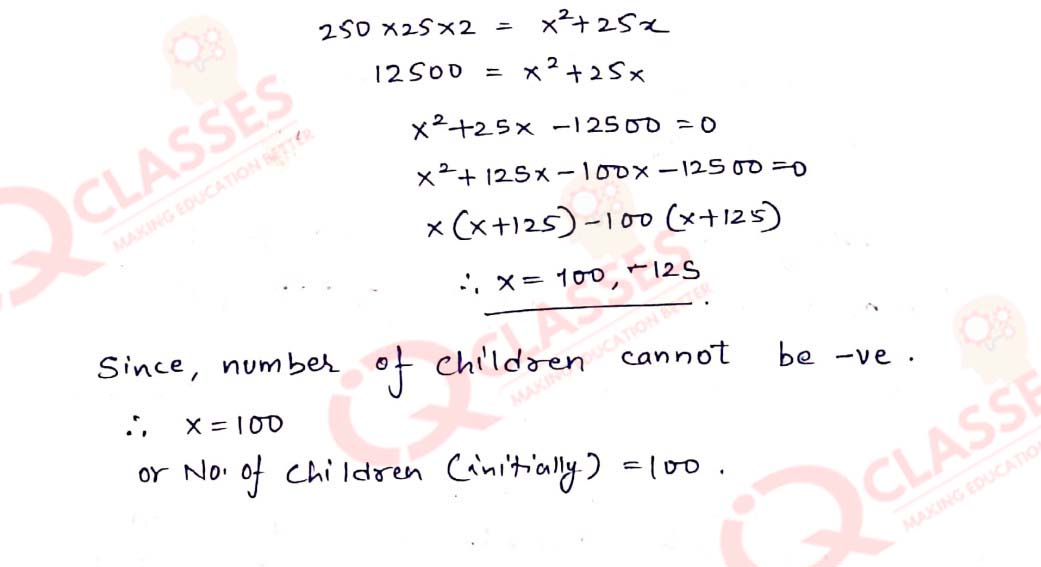
Q18 The total cost price of a certain number of identical articles is Rs4,800. By selling the articles at Rs100 each, a profit equal to the cost price of 15 articles is made. Find the number of articles bought.
Solution


Q19 The speed of a boat in still water is 15 km/hr. It can go 30 km upstream and return downstream to the original point in 4 hours 30 minutes. Find the speed of the stream.
Solution


Q20 A bus covers a distance of 240 km at a uniform speed. Due to heavy rain its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be 'x' km/h, form an equation and solve it to evaluate 'x'.
Solution

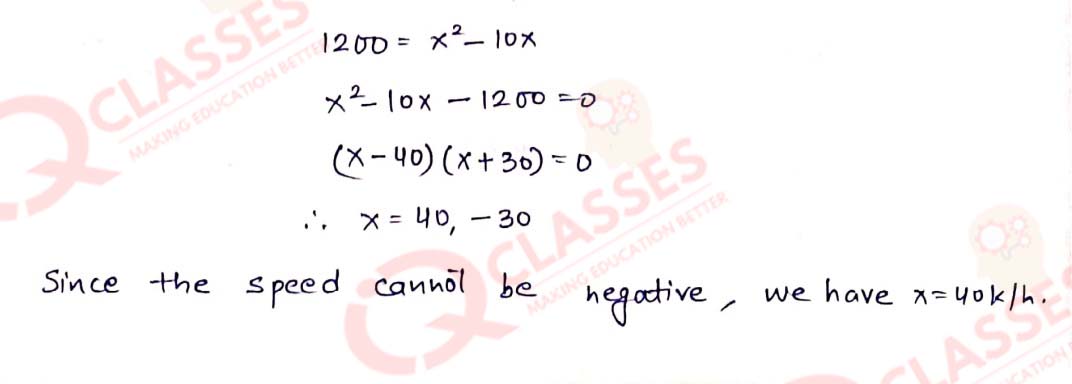
Q21 The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their ages in years is 550. Find their ages.
Solution
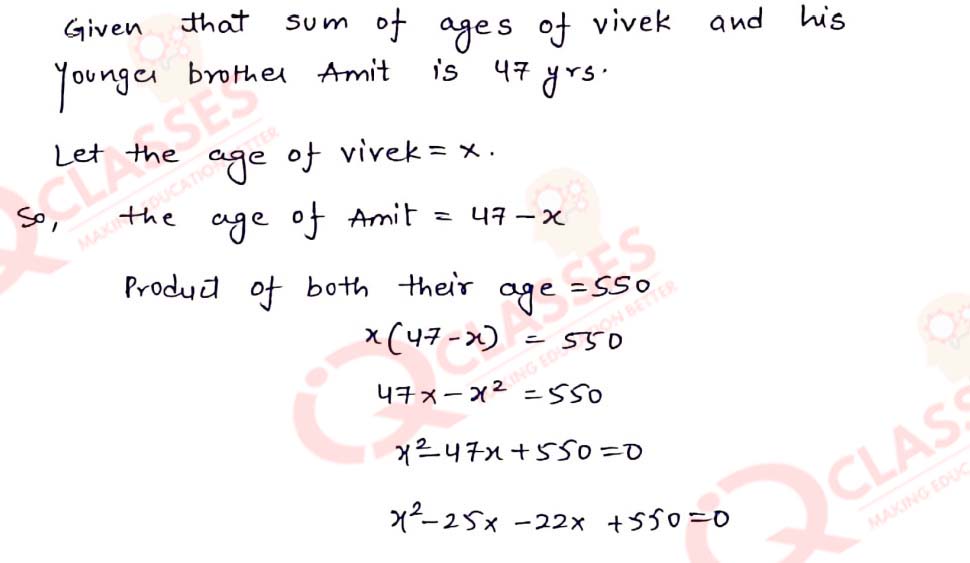

Q22 One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son's age. Find their present ages.
Solution

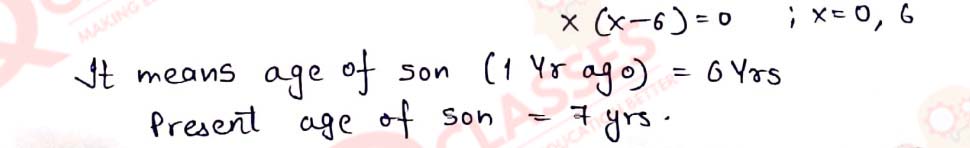

Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment