Class 10 ICSE Maths Remainder and Factor Theorem Important Questions
Remainder Theorem is an approach of Euclidean division of polynomials. According to this theorem, if we divide a polynomial P(x) by a factor ( x – a); that isn’t essentially an element of the polynomial; you will find a smaller polynomial along with a remainder. This remainder that has been obtained is actually a value of P(x) at x = a, specifically P(a). So basically, x -a is the divisor of P(x) if and only if P(a) = 0. It is applied to factorize polynomials of each degree in an elegant manner.
Class 10 ICSE Remainder and Factor Theorem Important Questions
Remainder and Factor Theorem Important Questions
Q.1 Find the remainder when x2 - 8x + 4 is divided by 2x + 1.
Solution

Q2 When the polynomial 2x3 - kx2 + (5k - 3)x - 8 is divided by x - 2, the remainder is 14. Find the value of 'k'.
Solution

Q3 When f(x) = x3 + ax2 - bx - 8 is divided by x - 2, the remainder is zero and when divided by x + 1, the remainder is —30. Find the values of 'a' and 'b'.
Solution


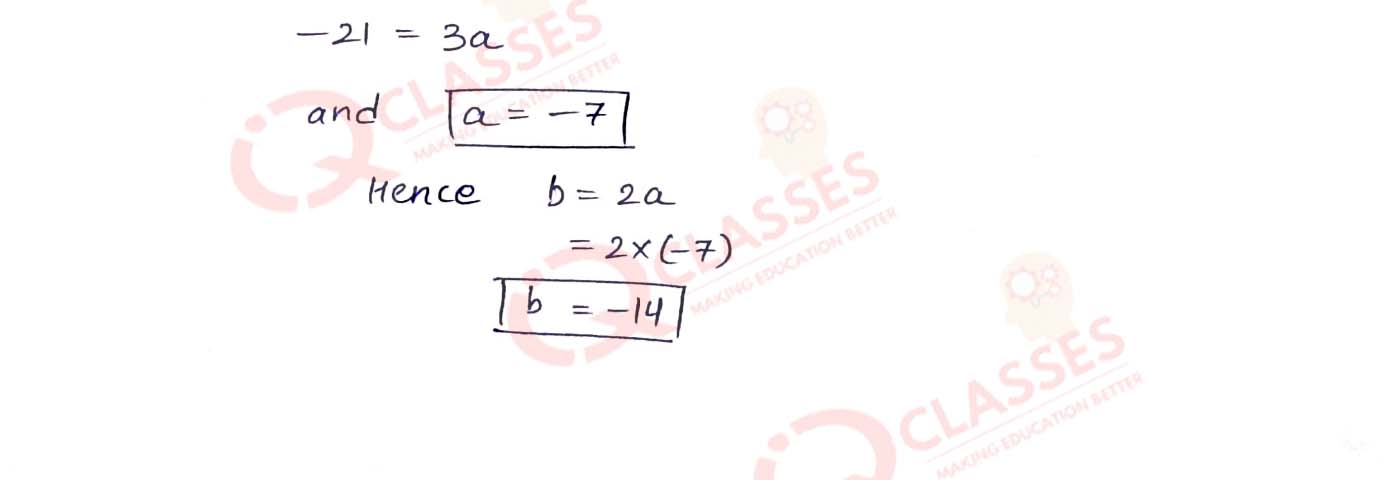
Q4 What number should be added to 2x3 — 3x2 + x so that when the resulting polynomial is divided by x - 2, the remainder is 3 ?
Solution

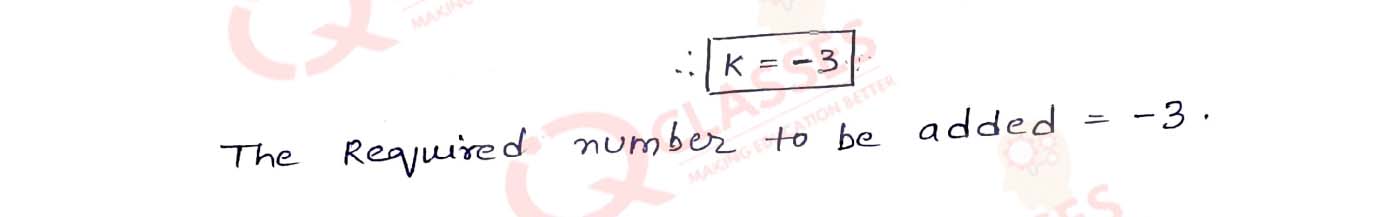
Q5 Find the value of 'k' if (x - 2) is a factor of x3 + 2x2 — kx + 10. Hence, determine whether (x + 5) is also a factor.
Solution

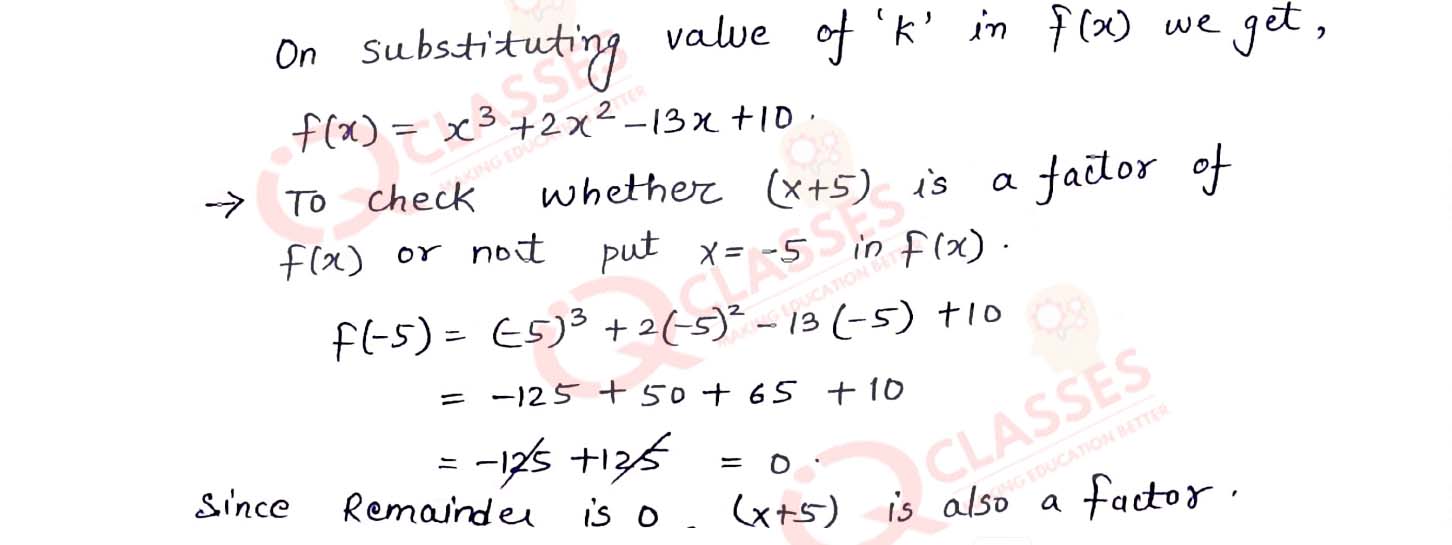
Q6
If (x - 2) is a factor of the expression 2x3 + ax2 + bx - 14 and when the
expression is divided by (x - 3), it leaves a remainder 52, find the values of a and b.
Solution



Q7
Find 'a' if the two polynomials ax3 + 3x2 — 9 and 2x + 4x + a,
leave the same remainder when divided by x + 3.
Solution


Q8
Polynomial x3 - ax2 + bx - 6 leaves remainder -8 when divided by x - 1 and x -
2 is a factor of it. Find the values of 'a' and 'b'.
Solution


Q9 Using the Remainder Theorem, factorise the expression 2x3 + x2 - 2x - 1 completely.
Solution

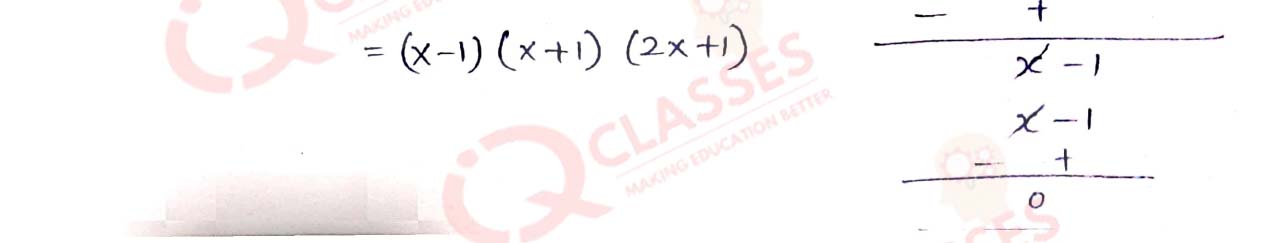
Q10
Find the values of 'a' and 'b' so that the polynomial x3 + ax2 + bx - 45 has
(x - 1) and (x + 5) as its factors. For the values of 'a' and 'b', as obtained above, factorise the
given polynomial completely.
Solution



Solution



Q11
If (x — 2) is a factor of 2x3 - x2 - px - 2
(i) find the value of p.
(ii) with the value of p, factorise the above expression completely.
Solution


Q12
If x + a is a common factor of expressions f(x) = x2 + px + q and g(x) = x2 +
mx + n;
Show that : a = (n-q)/(m-p)
Solution



Q13
Find the number that must be subtracted from the polynomial 3y3 + y2 - 22y +
15, so that the resulting polynomial is completely divisible by y + 3.
Solution
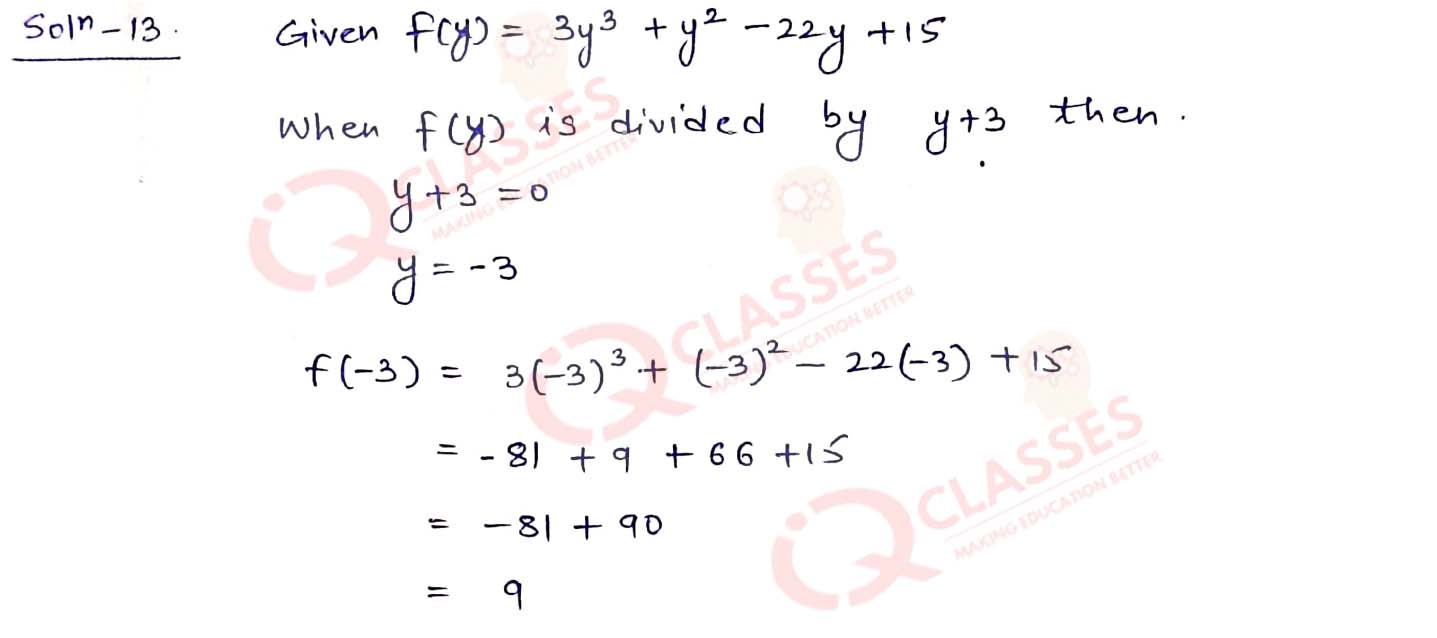

Q14
Find the value of 'a' if the division of ax3 + 9x2 + 4x - 10 by x + 3 leaves a
remainder of 5.
Solution


Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment