Class 10 ICSE Maths Section Formula Important Questions
A point on the line segment divides it into two parts which may equal or not. The ratio in which the point
divides the given line segment can be found if we know the coordinates of that point. Also, it is possible to
find the point of division if we know the ratio in which the line segment joining two points has given. These
two things can be achieved with the help of a section formula in coordinate geometry.
Section formula is used to determine the coordinate of a point that divides a line segment joining two
points into two parts such that the ratio of their length is m:n.
Q.1
Find the distance between the points P(-4, 7) and Q(2, -5).
Solution


Q2
Find the distance of the point P(6, -6)from the origin.
Solution


Q3
If the point. P(k-1,2) is equidistant from the points A(3, k) and B(k,5), find the values of k.
Solution

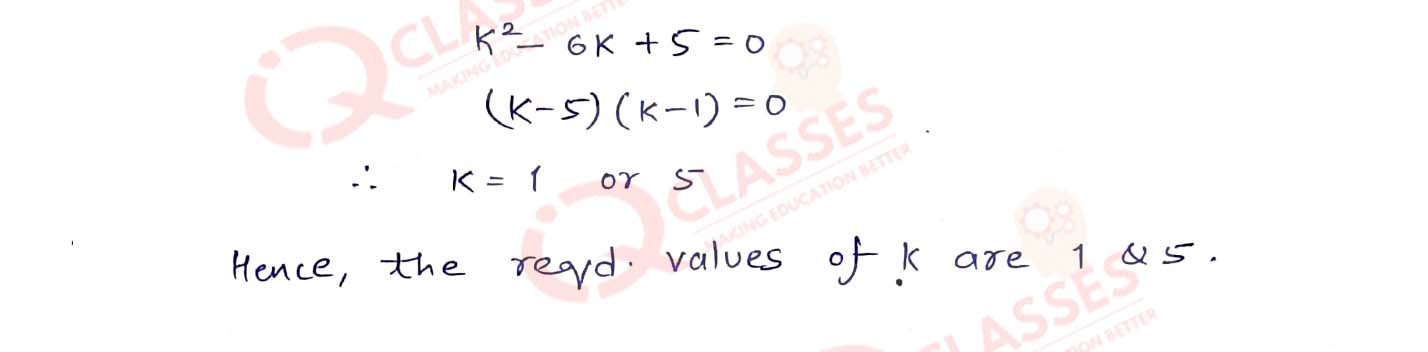

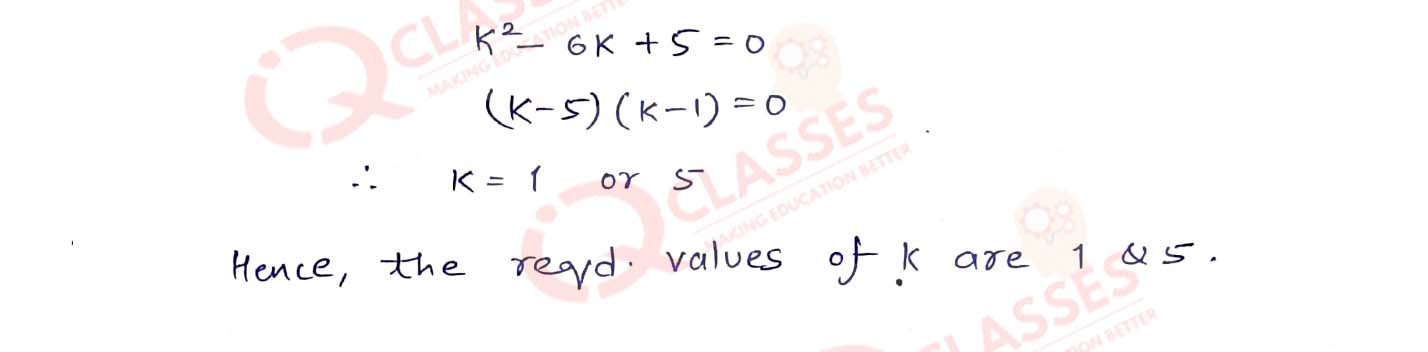
Q4
Find those points on the y-axis, each of which is at a distance of 13 units from the point A(-5,7).
Solution




Q5
Find the centre of a circle passing through the points (6, -6), (3, -7) and (3, 3).
Solution




Q6
Show that the points (a,a), (-a, -a) and (-√3a, √3a) are the vertices of an equilateral
triangle. Find its area.
Solution






Q7
Show that the points (1, 1), (-1, 5), (7, 9) and (9, 5) taken in that order arc the vertices of a
rectangle. Also, find the area of the rectangle.
Solution










Q8
Prove that the points A(1, 1), B(-2, 7) and C(3, -3) are collinear.
Solution

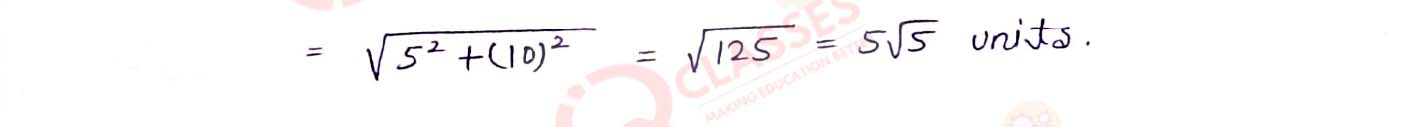
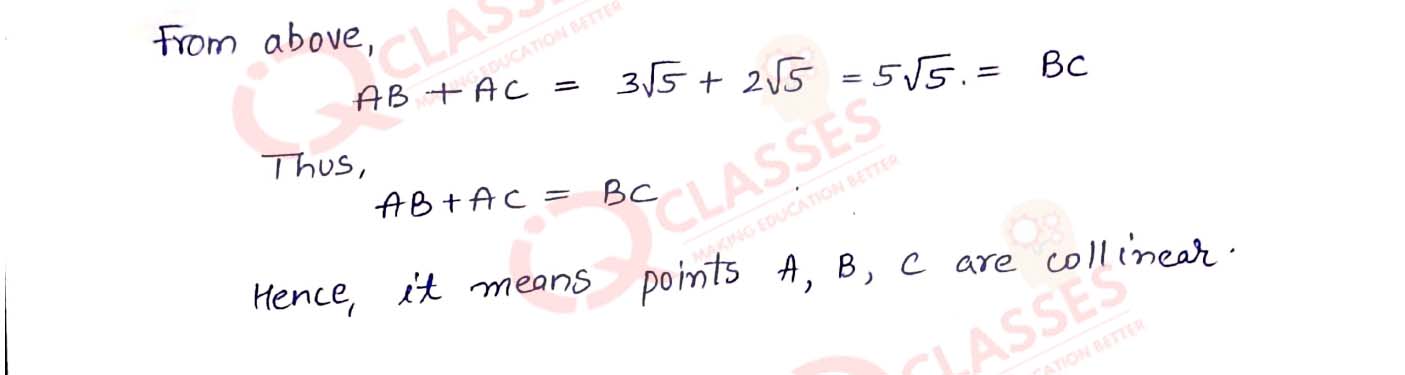

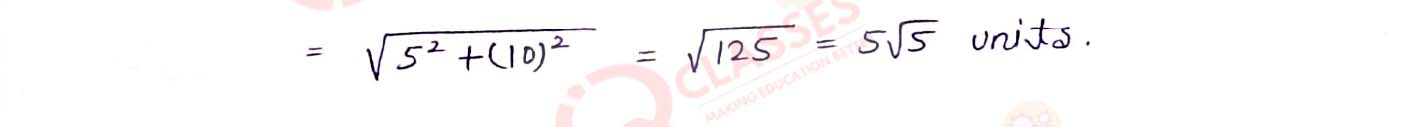
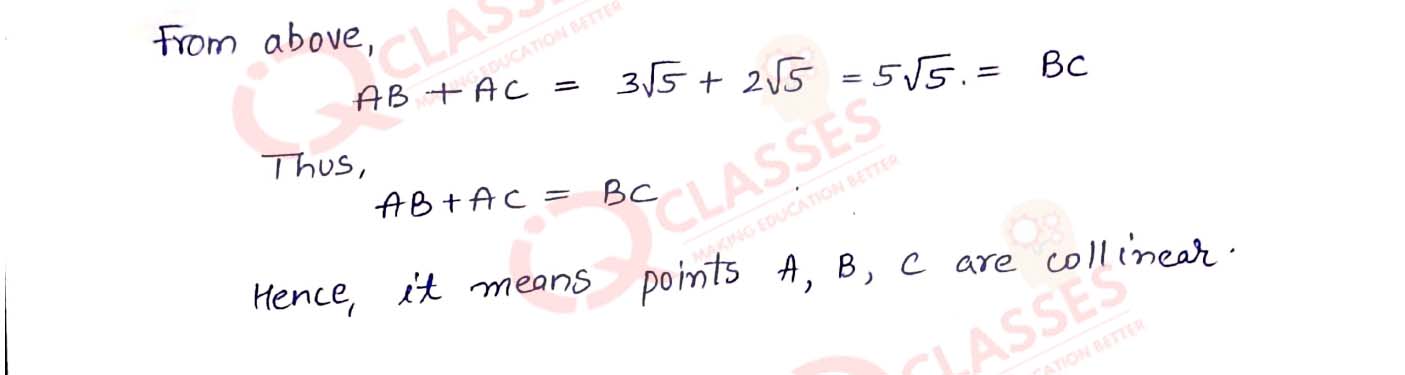
Q9
Find the coordinates of the points of trisection of the line segment joining the points A(-5, 6) and
B(4, -3).
Solution




Q10
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6 ,7) such that AP =


2
/
5
AB.
Solution


Q11
Point P divides the line segment joining the points A(2,1) and B(5, -8) such that 

AP
/
AB
=
1
/
3
P lies on the line 2x - y + k = 0, find
Solution


Q12
Find the ratio in which the point P(11, y) divides the line segment coining the points A(15, 5) and
B(9, 20). Also, find the value of y.
Solution




Q13
let D(3, -2), E(-3, 1) and F(4, -3) be the midpoints of the sides BC, CA and AB respectively of
△ABC. Then, find the coordinates of the vertices A, B and C.
Solution


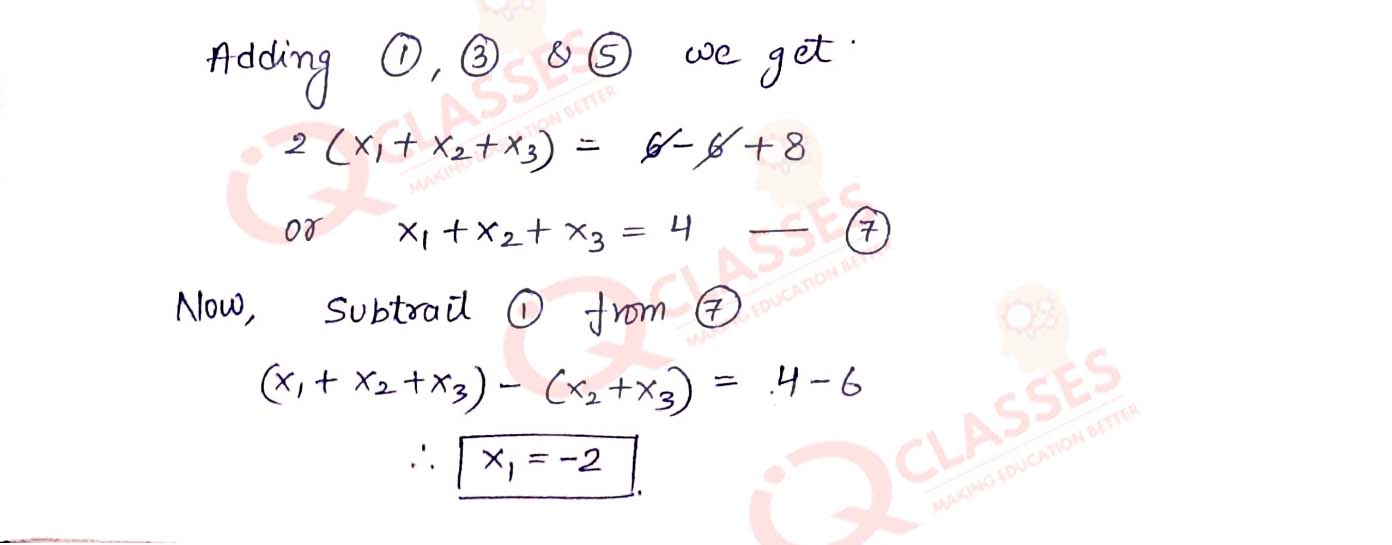

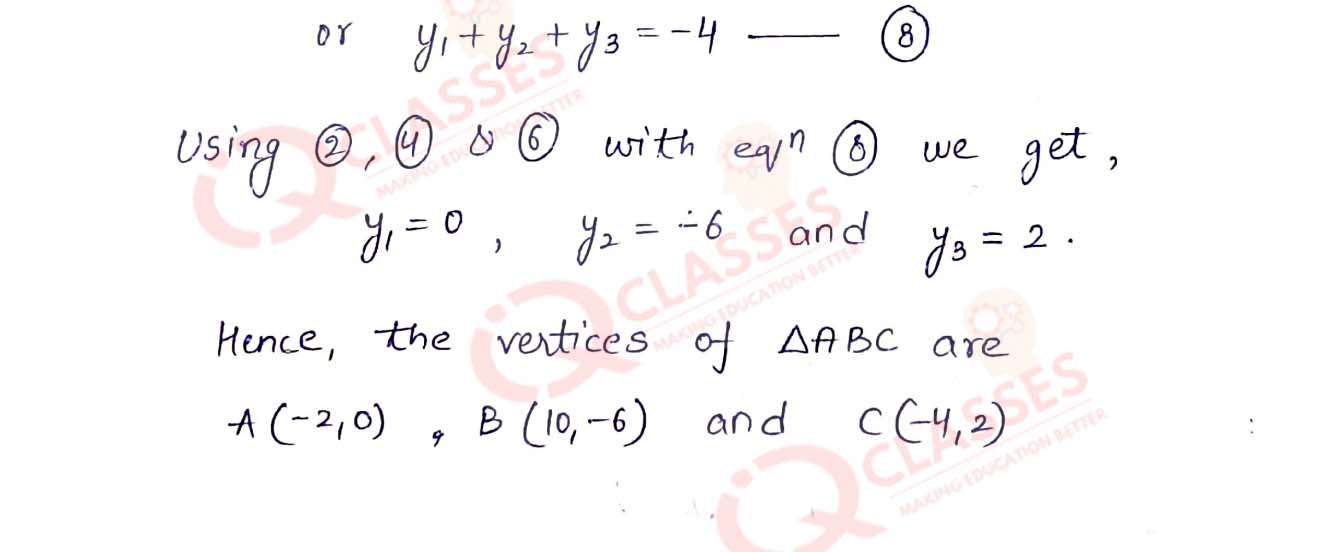


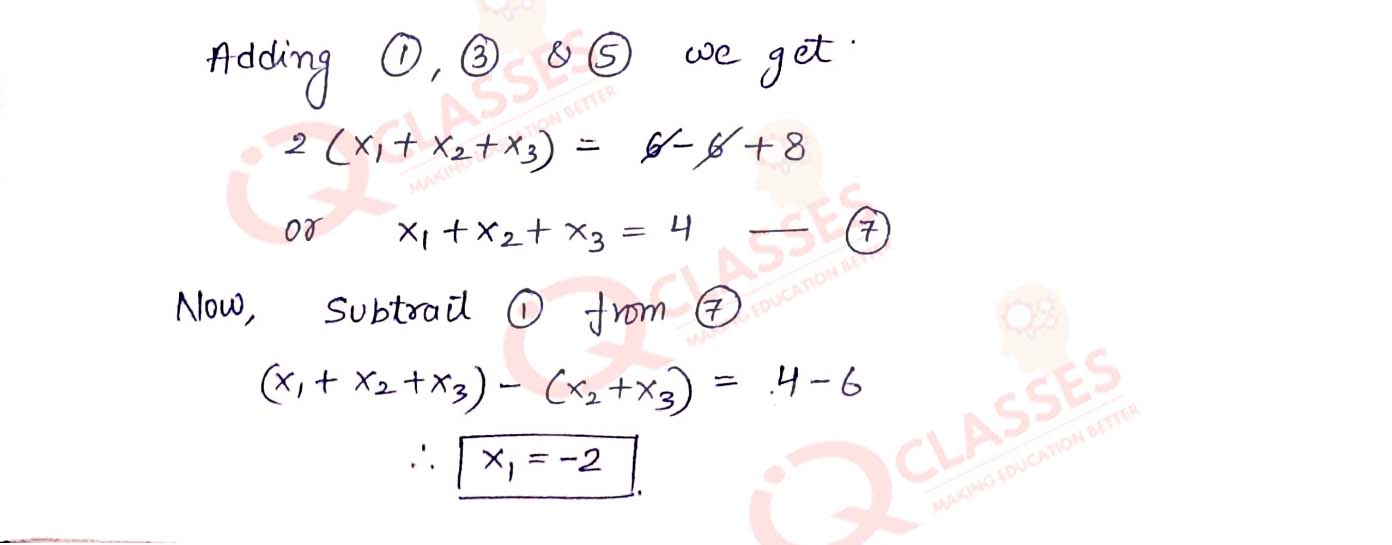

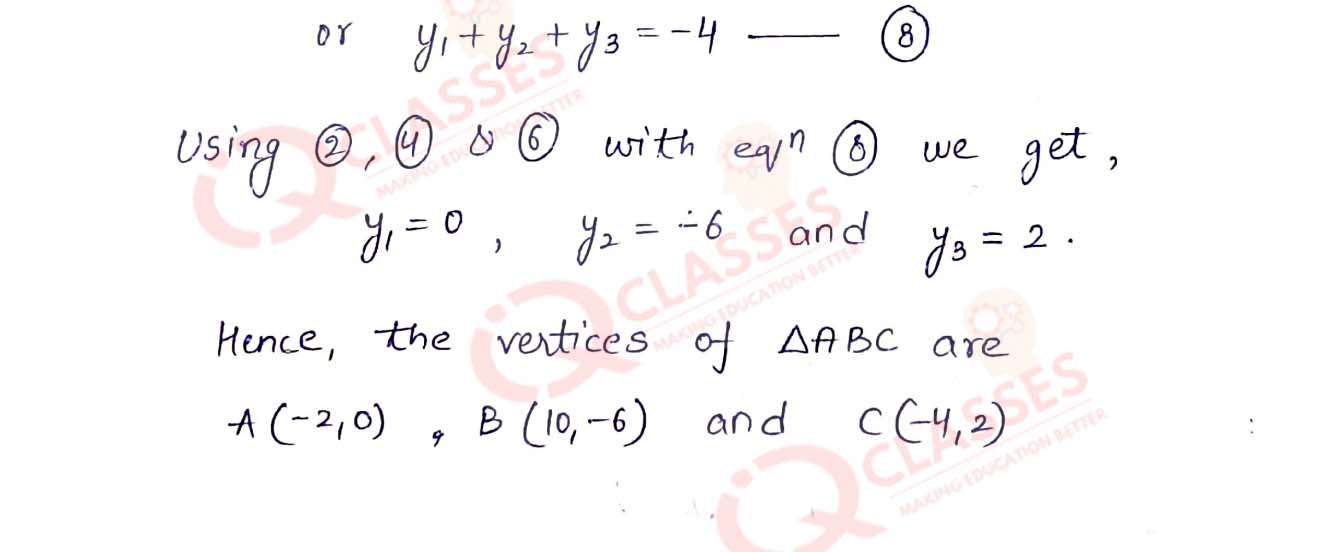
Q14
Two vertices of a △ABC are given by A(6, 4) and B(-2, 2), and its centroid is G(3, 4). Find
the coordinates of the third vertex C of △ABC.
Solution




Q15
The coordinates of one end point of a diameter AB of a circle are A(4, -1) and the coordinates of
the center of the circle are C(1, -3), Find the coordinates of B.
Solution





Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment