Class 12 CBSE Maths Continuity & Differentiability Board Questions
Continuity and differentiability in class 12 is about, if a function f(x) is said to be continuous at a point x = a, if Left hand limit of f(x) at(x = a) = Right hand limit of f(x) at (x = a) = Value of f(x) at (x = a) i.e. if at x = a, LHL = RHL = f(a)
2016
Q1
Find the values of p and q, for which
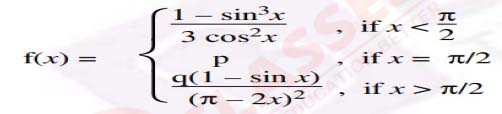
is continuous at x = π/2.
solutions



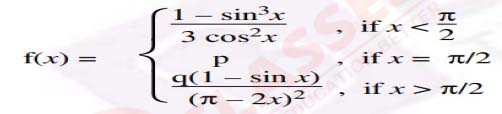
is continuous at x = π/2.
solutions




2017
Q1
Find the value of c in Rolle's theorem for the function f(x) = x3— 3x in [-√3,0]
solutions

solutions


Q2
Determine the value of 'k' for which the following function is continuous at x=3:

solutions
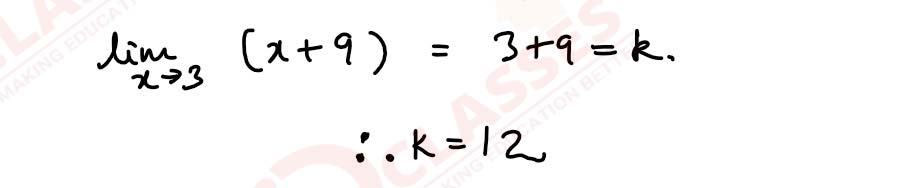

solutions

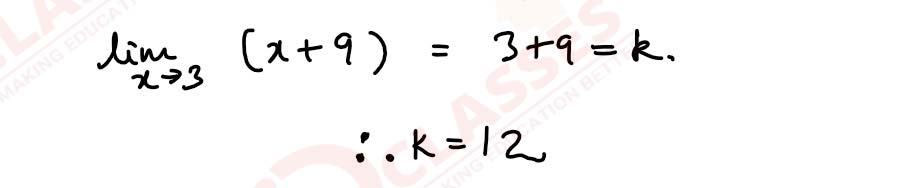
2020
Q1
The greatest integer function defined by f(x) = [x], 0 < x < 2 is not differentiable at x=_______
solutions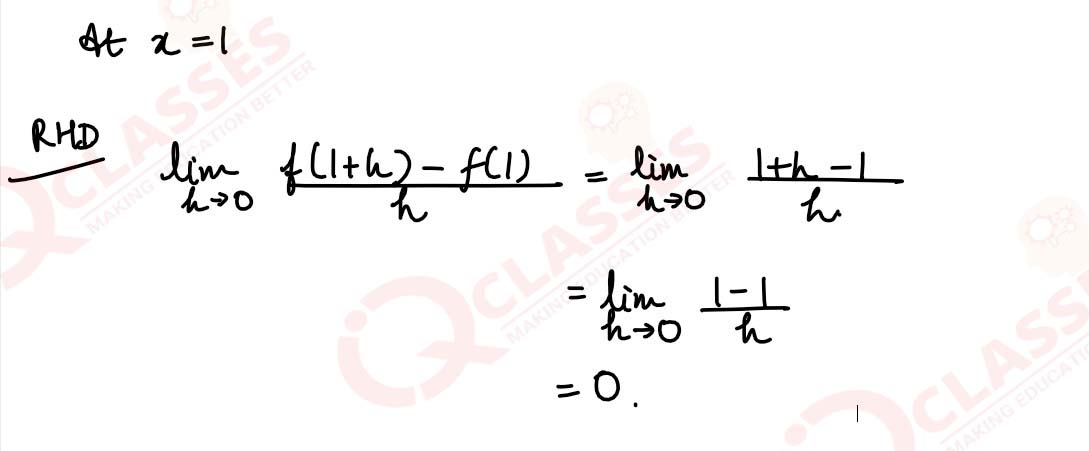
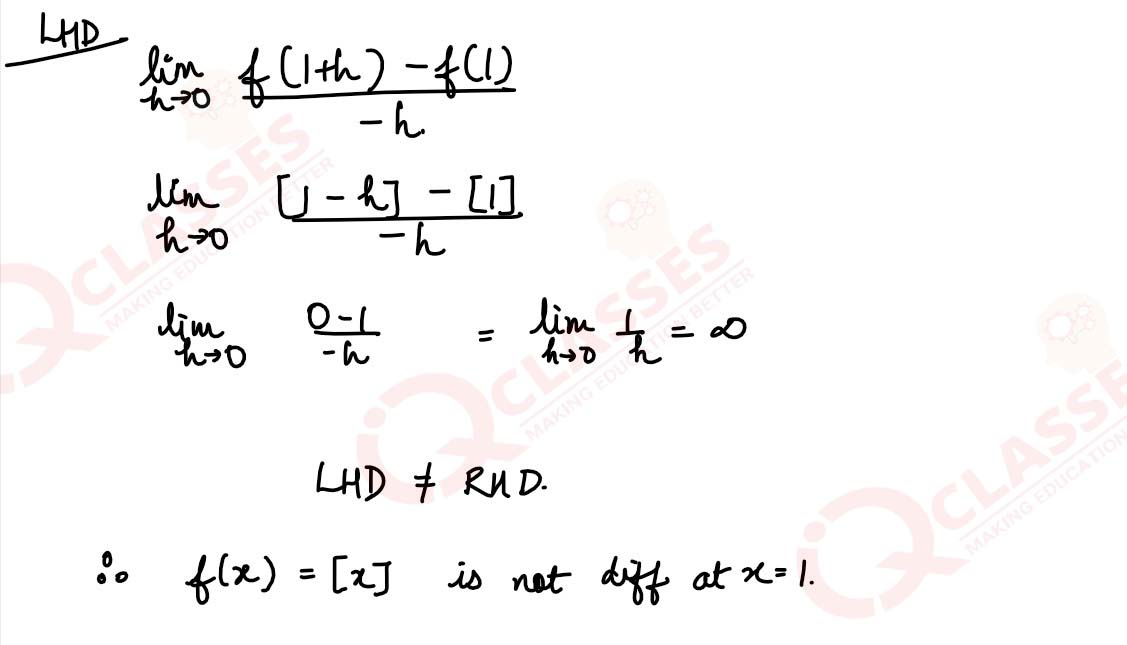
solutions
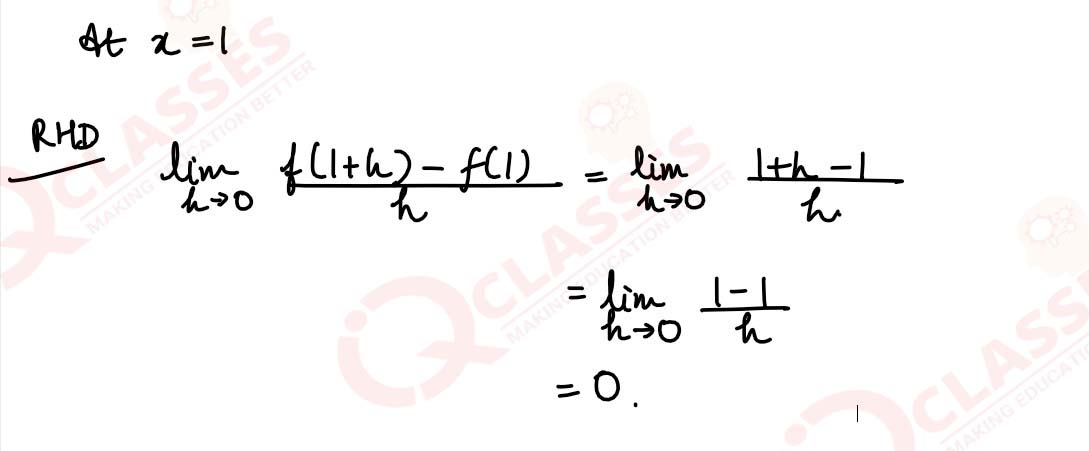
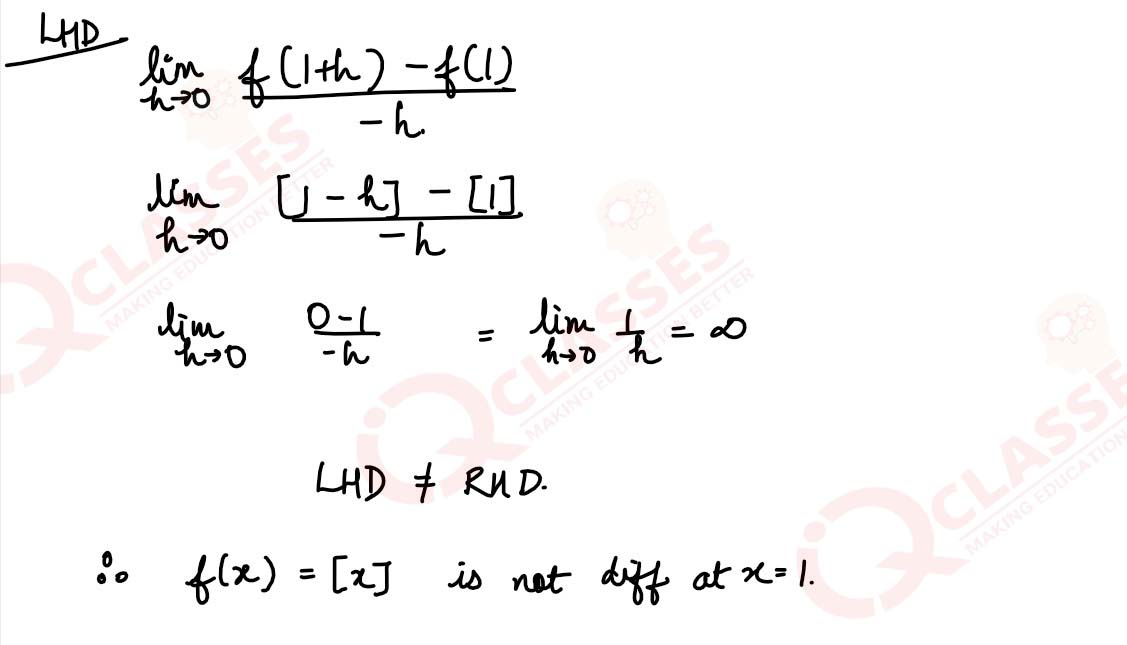
Differentiation
2016
Q1
If x = a sin 2t( 1 + cos 2t) and y = b cos 2t ( 1 - cos 2t), find the values of
OR
if y = xx prove that
solutions


dy
/
dx
at t =
π
/
4
and t =
π
/
3
if y = xx prove that
d2y
/
dx2
-
1
/
y
(
dy
/
dx
)2 -
y
/
x
= 0
solutions



2017
Q2
if xy + yx = ab then find
OR
If ey(x + 1) = 1, then show that
solutions
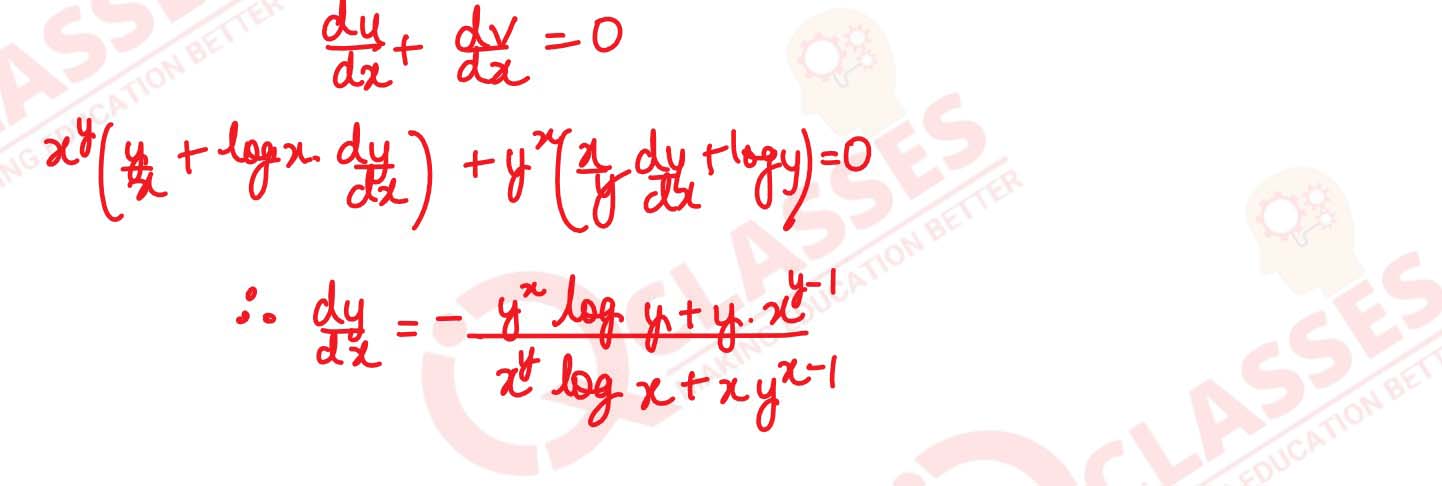
dy
/
dx
If ey(x + 1) = 1, then show that
d2y
/
dx2
= (
dy
/
dx
)2
solutions

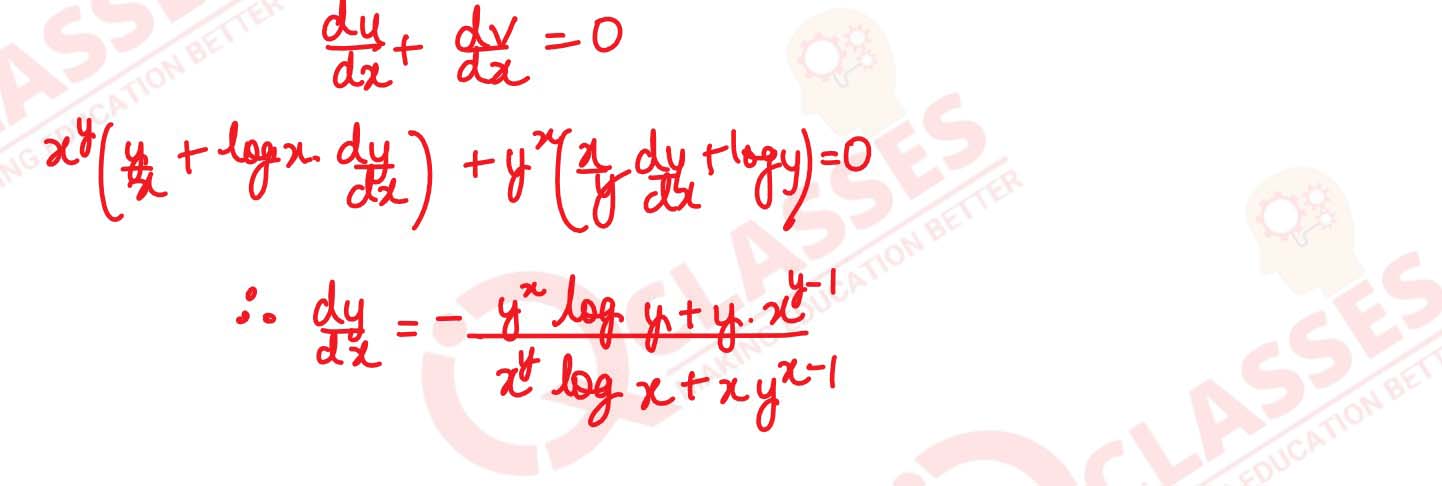
2018
Q3
If log(x2 + y2) = 2 tan-1(
OR
If xy - yx = ab, find
solutions
y
/
x
), show that
dy
/
dx
=
x + y
/
x - y
If xy - yx = ab, find
dy
/
dx
solutions

Q4
If f(x) = x+ 1, find
solutions
d
/
dx
(fof)(x)
solutions

Q5
If y = (sin-1x)2 , prove that ( 1- x2)
solutions
d2y
/
dx2
- x
dy
/
dx
- 2 = 0
solutions

2019
Q6
If sin y = x cos(a + y), then show that
Also show that
solutions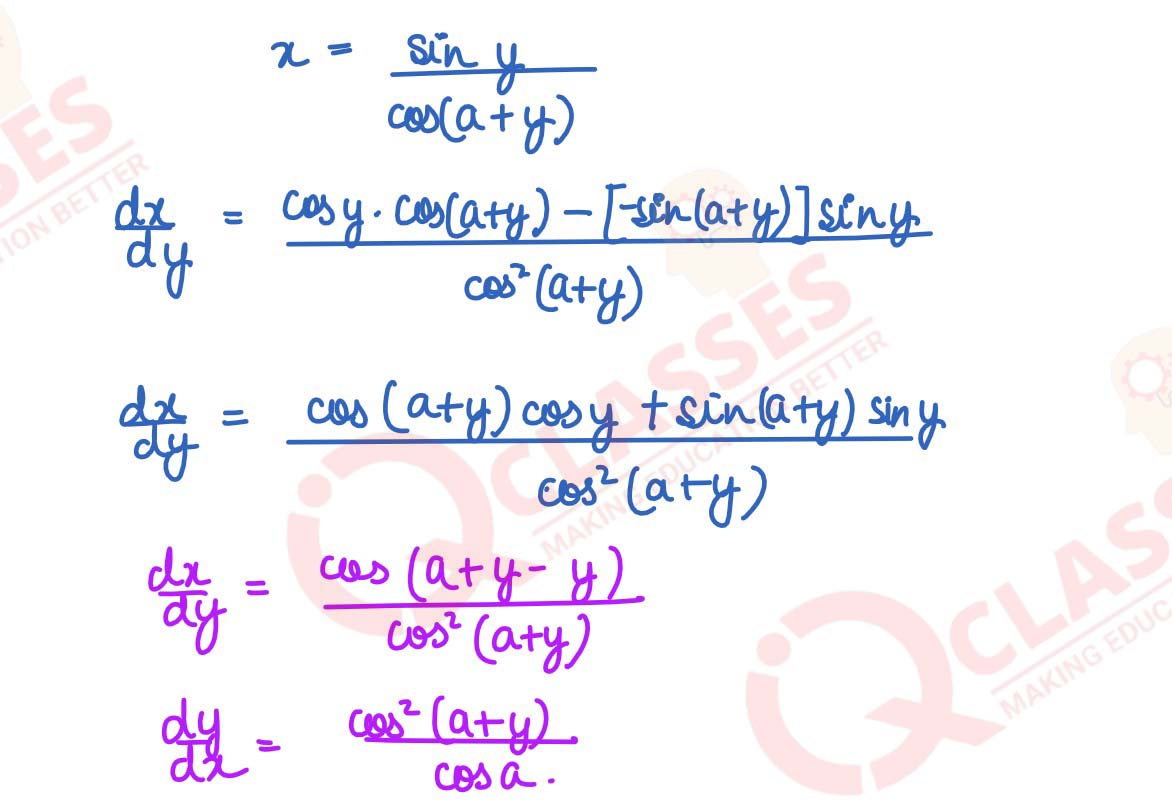
dy
/
dx
=
cos2(a + y)
/
cos a
Also show that
dy
/
dx
= cos a, when x = 0
solutions
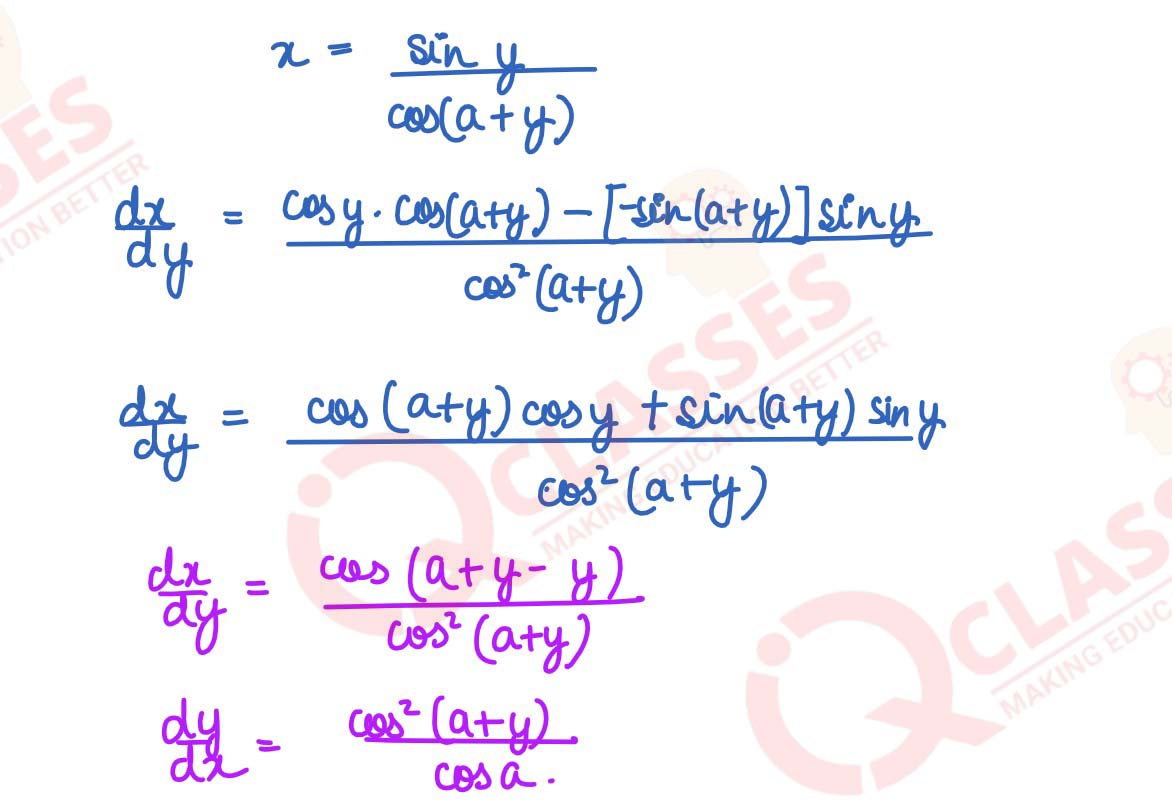
Q7
Differentiate tan-1 (
solutions
cosx - sinx
/
cosx + sinx
) with respect to x.
solutions

Q8
If x = a sec3 θ and y = a tan3 θ, find
OR
If y = etan-1x prove that ( 1+ x2)
solutions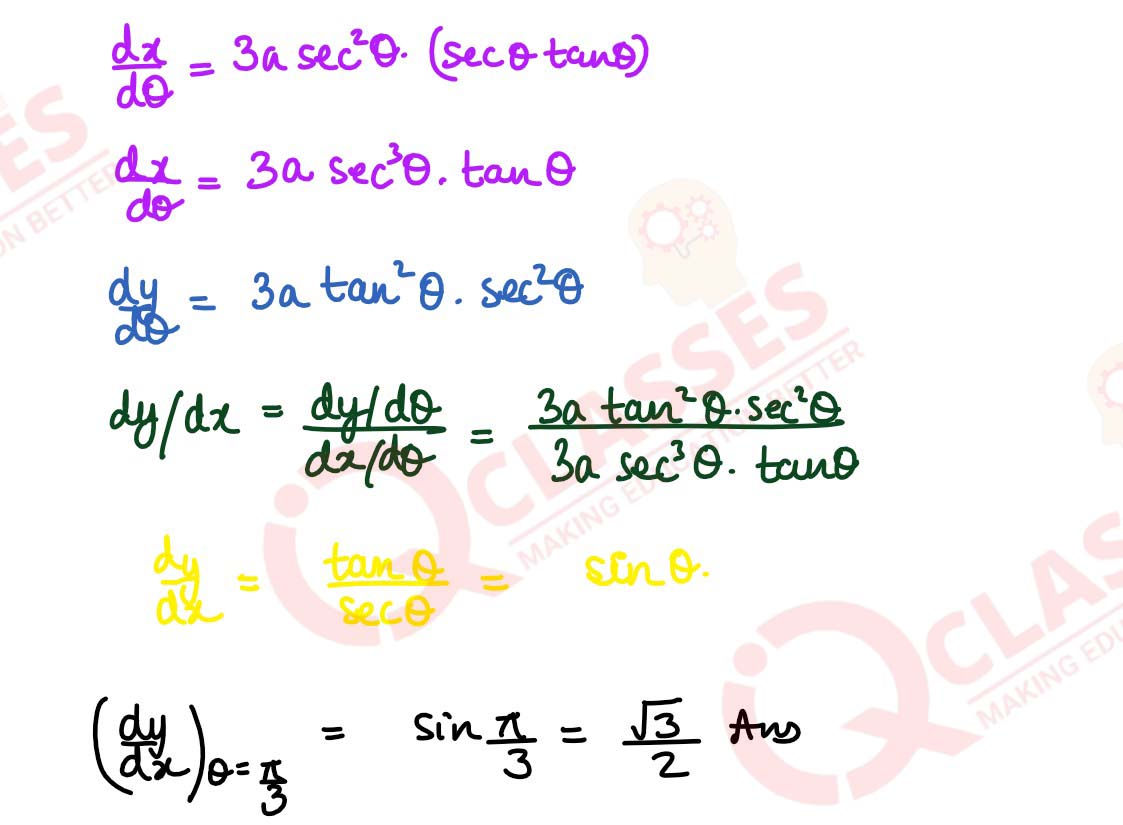

d2y
/
dx2
at θ = π/3If y = etan-1x prove that ( 1+ x2)
d2y
/
dx2
+ (2x - 1)
dy
/
dx
= 0
solutions
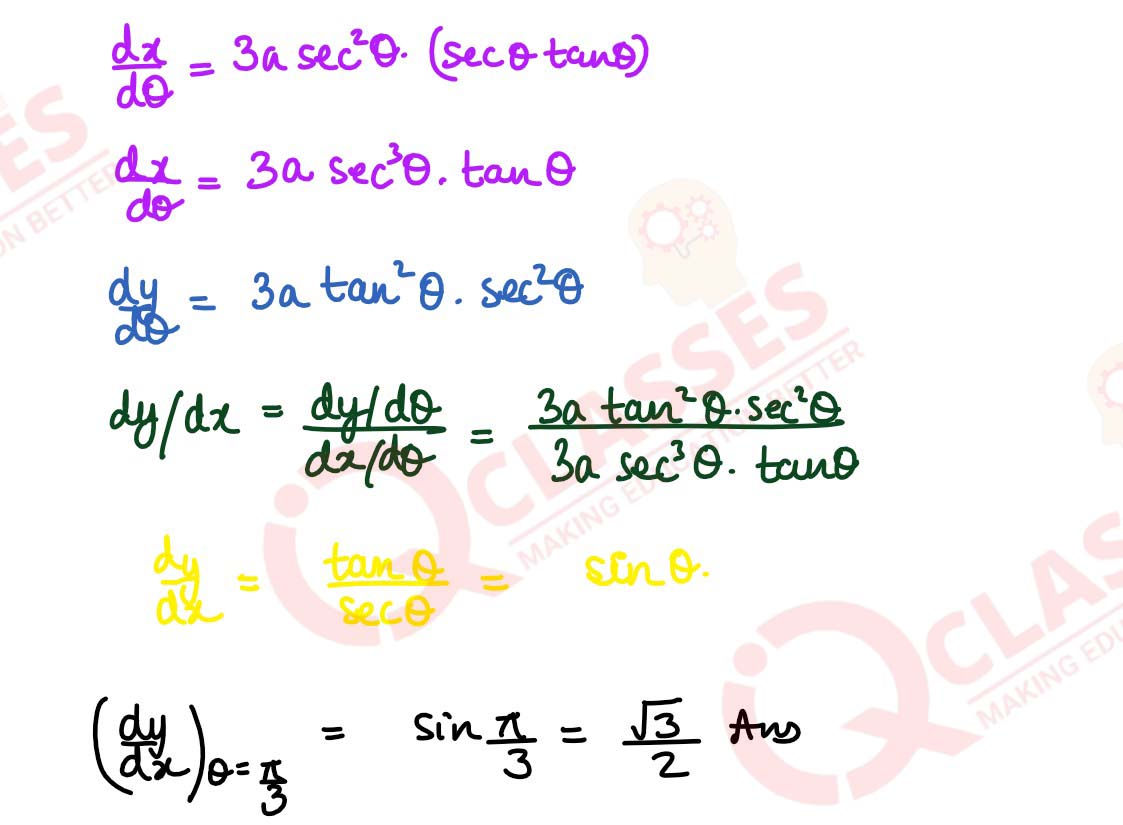

2020
Q9
If x = at2, y = 2at then find
solutions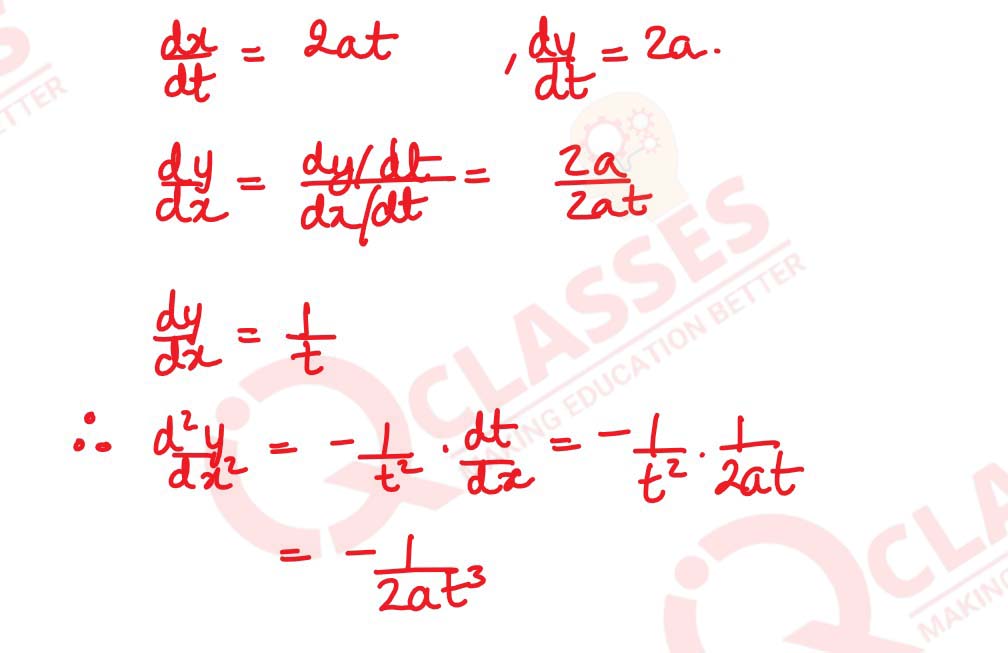
d2y
/
dx2
solutions
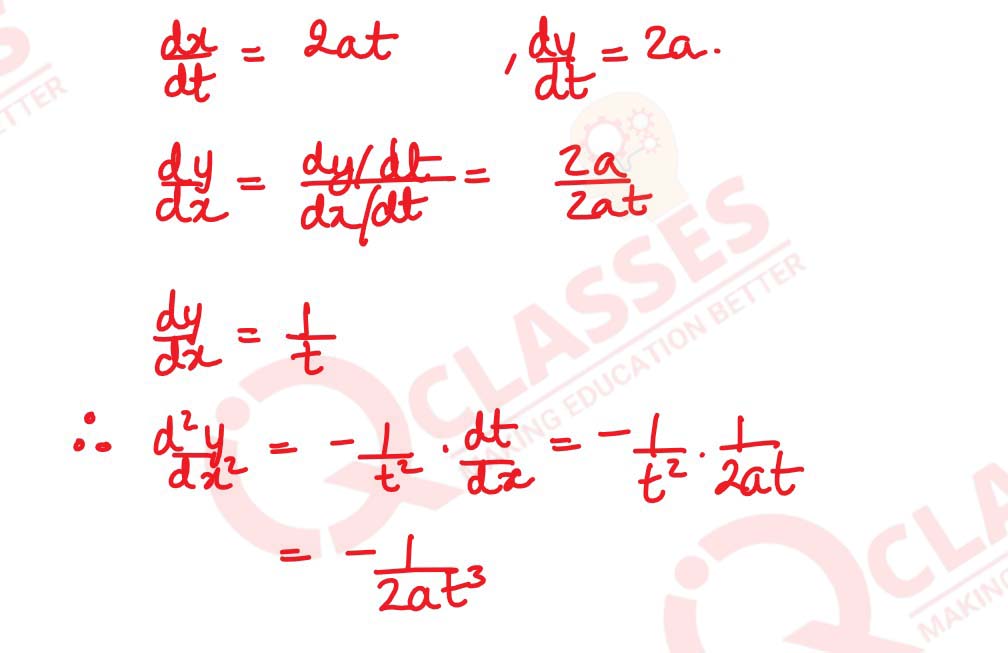
Q10
If y = ex2cosx + (cos x)x, then find
solutions
dy
/
dx
solutions



Add a comment