Class 12 Maths CBSE Differential Equations Board Questions
Here we provide Class 12 maths important notes,board questions and predicted questions with Answers for chapter Differential Equations. These important notes,board questions and predicted questions are based on CBSE board curriculum and correspond to the most recent Class 12 maths syllabus. By practising these Class 12 materials, students will be able to quickly review all of the ideas covered in the chapter and prepare for the Class 12 Board examinations.
Class 12 CBSE Differential Equations Board Questions
Differential Equations Board Questions
Differential Equations
2016
Q1
(a) Find the particular solution of the differential equation
(1 - y2)(1 + log x)dx + 2xy dy = 0 , given that y = 0 when x = 1
(b) Find the general solution of the following differential equation :
(1 + y2) + ( x - etan-1y)
solutions
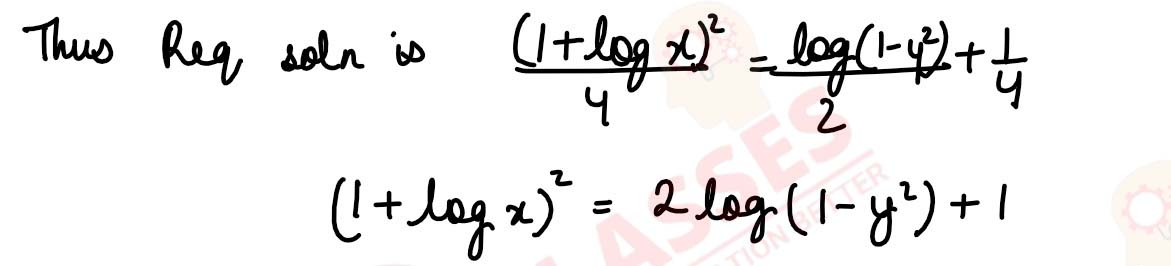

(1 - y2)(1 + log x)dx + 2xy dy = 0 , given that y = 0 when x = 1
(b) Find the general solution of the following differential equation :
(1 + y2) + ( x - etan-1y)
dy
/
dx
= 0
solutions


2017
Q2
Solve the differential equation ( tan-1 x - y)dx = ( 1+ x2)dy
solutions
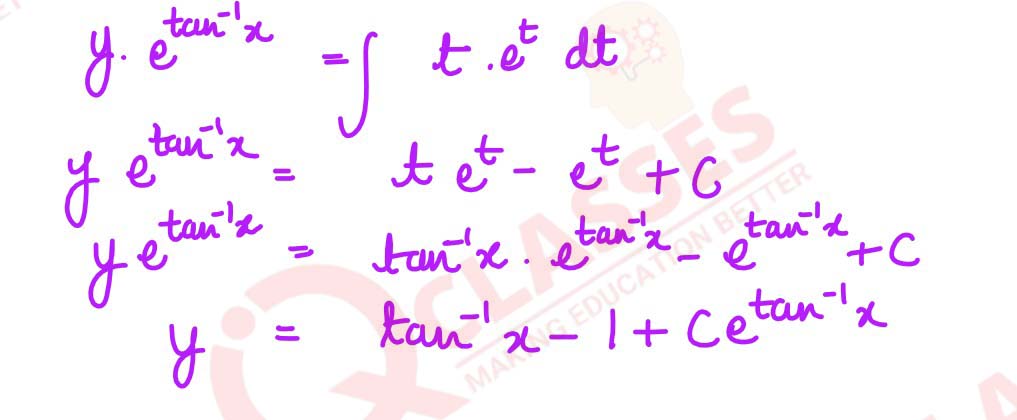
solutions

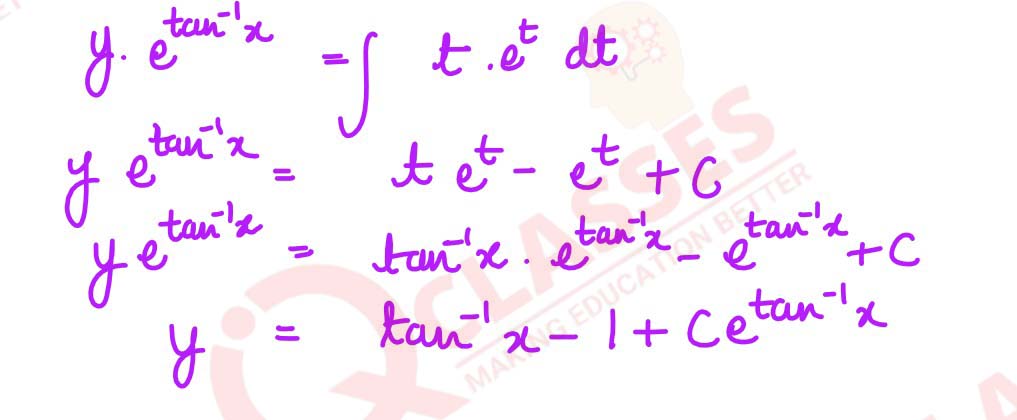
Q3
Find the particular solution of the differential equation ( x- y)
solutions


dy
/
dx
= ( x + 2y), given that y = 0 when x = 1
solutions



2018
Q4
From the differential equation representing the family of curves y = e2x ( a + bx) where
a and b are arbitrary constants
solutions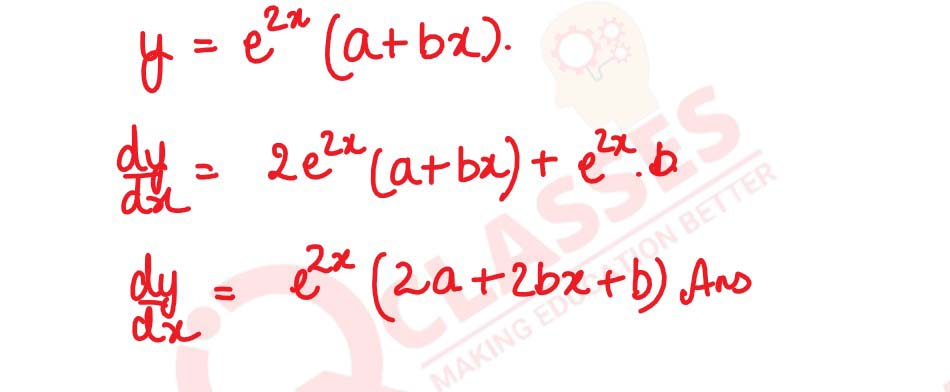
solutions
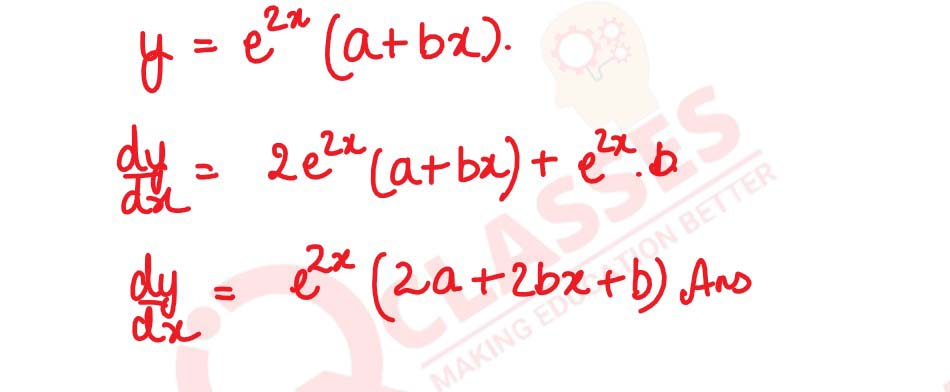
Q5
Find the order and degree of the differential equation : x2
solutions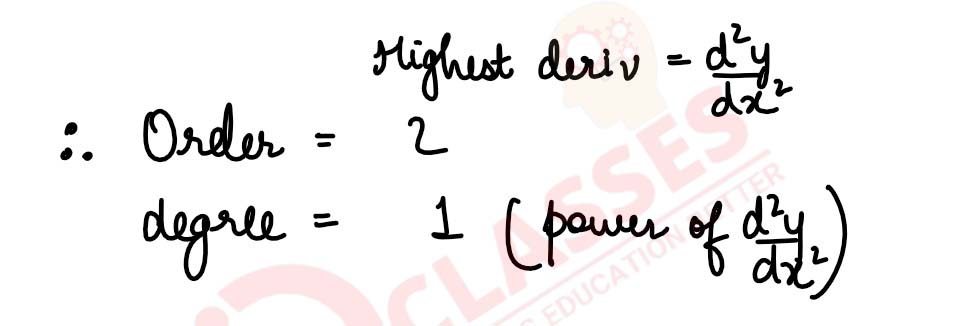
d2y
/
dx2
= { 1 + (
dy
/
dx
)2}4
solutions
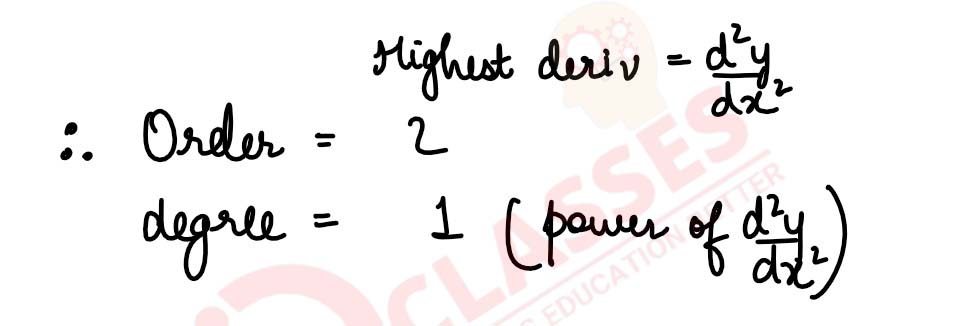
Q6
Solve the differential equation xdy - ydx = √x2 + y2 dx, given that y =0
when x = 1
OR
Solve the differential equation : (1 + x2)
solutions


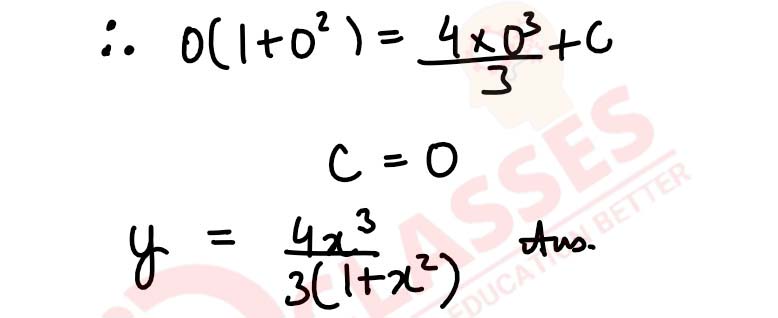
Solve the differential equation : (1 + x2)
dy
/
dx
+ 2xy - 4x2 = 0, subject to the initial y(0) = 0
solutions



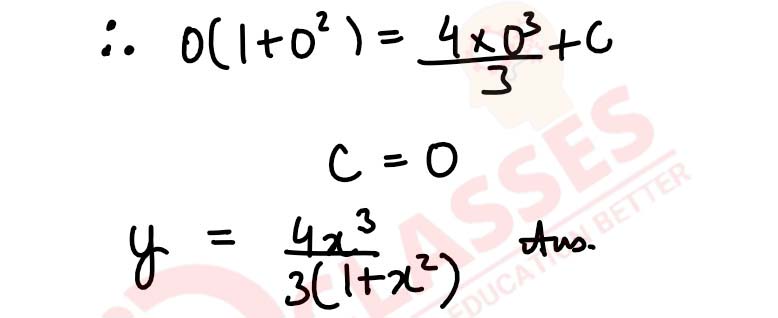
2019
Q7
Solve the differential equation cos(
solutions
dy
/
dx
) = a, (a ∈ R)
solutions

Q8
Solve the differential equation (x2 - y2)dx + 2xydy = 0
OR
Find the particular solution of differential equation (1 + x2)
solutions



Find the particular solution of differential equation (1 + x2)
dy
/
dx
+ 2xy =
1
/
1 + x2
given that y = 0 when x = 1
solutions




2020
Q9
The number of arbitrary constants in the particular solution of differential equation of second
order is (are)
(A) 0
(B) 1
(C) 2
(D) 3
solutions
(A) 0
(B) 1
(C) 2
(D) 3
solutions

Q10
Find the general solution of the differential equation
y eydx = (y3 + 2x ey) dy
OR
Find the particular solution of the differential equation
x
solutions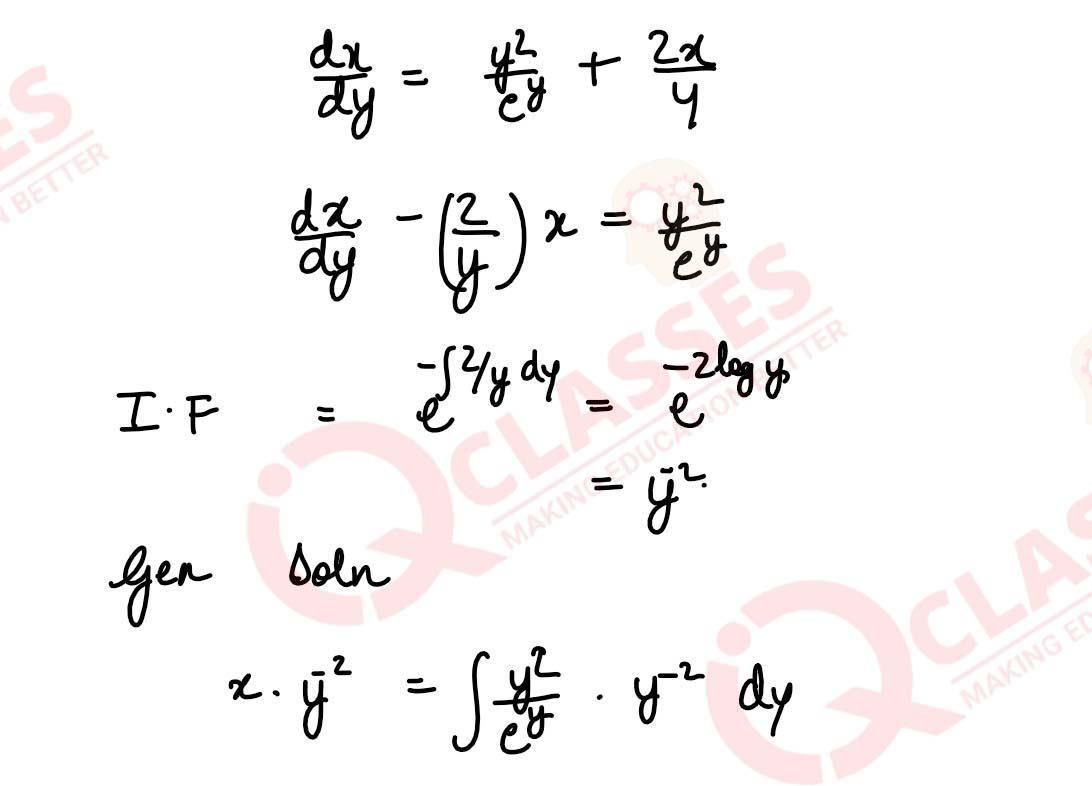




y eydx = (y3 + 2x ey) dy
Find the particular solution of the differential equation
x
dy
/
dx
= y - x tan(
y
/
x
) , given that y =
π
/
4
at x = 1
solutions





Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment