Class 12 CBSE Maths integration Board Questions
Integration is called the inverse process of differentiation. Instead of differentiating a function, we are given the function’s derivative and asked to find its primitive, i.e., the original function. Such a process is called integration or anti-differentiation. If the function’s derivative is known to us, is it possible to obtain the function. The answer to this question is yes. Integration ( or antiderivative of a function) makes it possible to obtain the original function.
2016
Q1
Find
∫
OR
Evaluate ∫ π0 e2x.sin (π/4 + x)dx
solutions




(3 sinθ -2) cos θ
/
5- cos2θ - 4 sinθ
dθ
OR
Evaluate ∫ π0 e2x.sin (π/4 + x)dx
solutions





Q2
Find
∫
solutions
√x
/
√a3-x3
dx
solutions

Q3
Evaluate
∫
2 -1
|x3 -x | dx
solutions
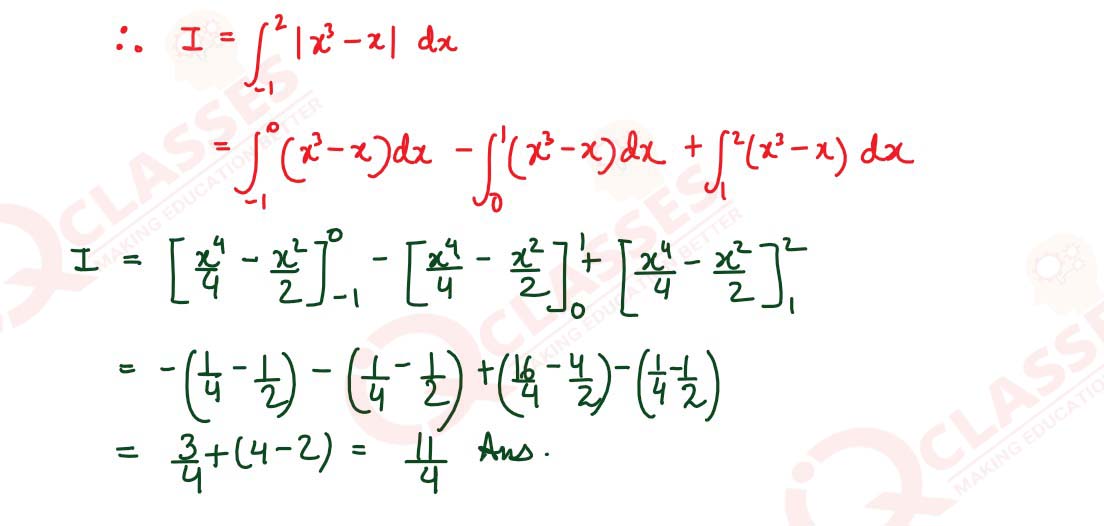
solutions

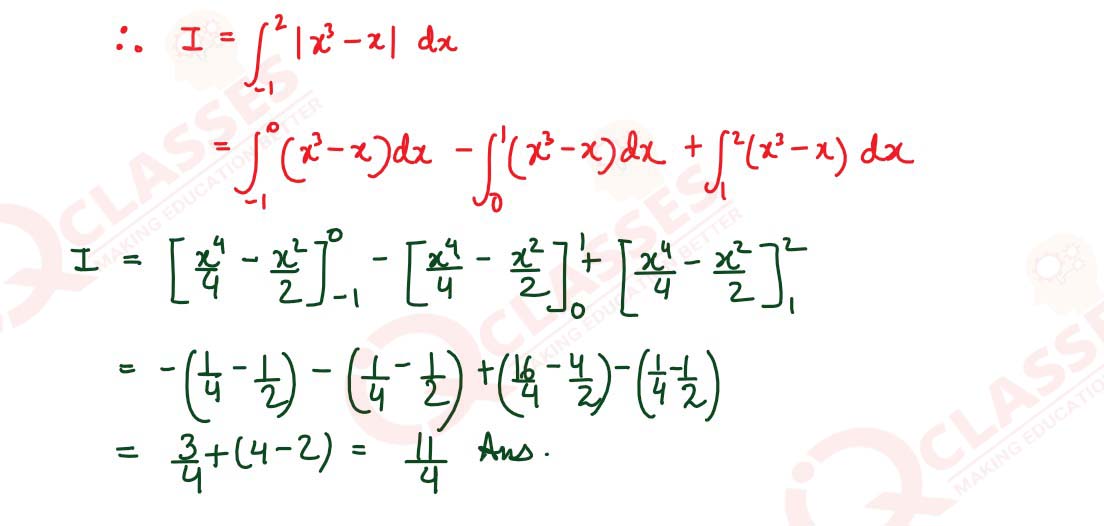
2017
Q1
Find
∫
solutions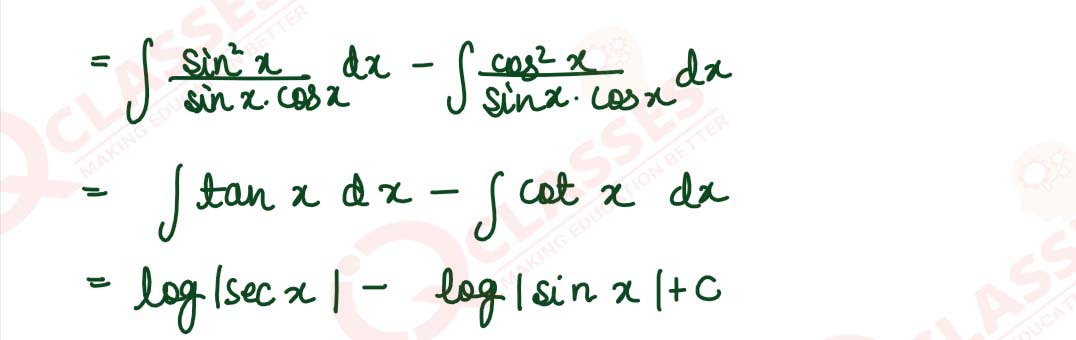
∫
sin2x - cos2 x
/
sin x cos x
dx
solutions
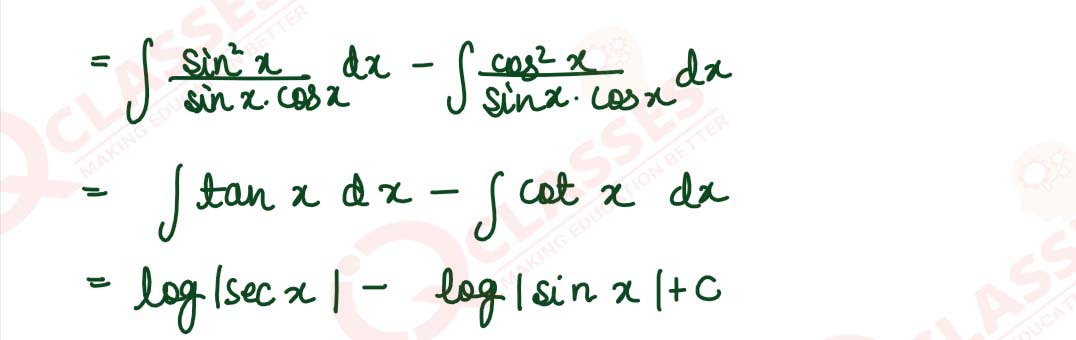
Q2
Find:
∫
solutions

∫
dx
/
5- 8x - x2
solutions


Q3
Find:
∫
solutions

∫
cos θ
/
(4+ sin2 θ)(5-4 cos 2 θ)
dθ
solutions


Q4
Evaluate:
∫ 4 1 {|x-1| + |x-2| + |x-4|} dx
solutions

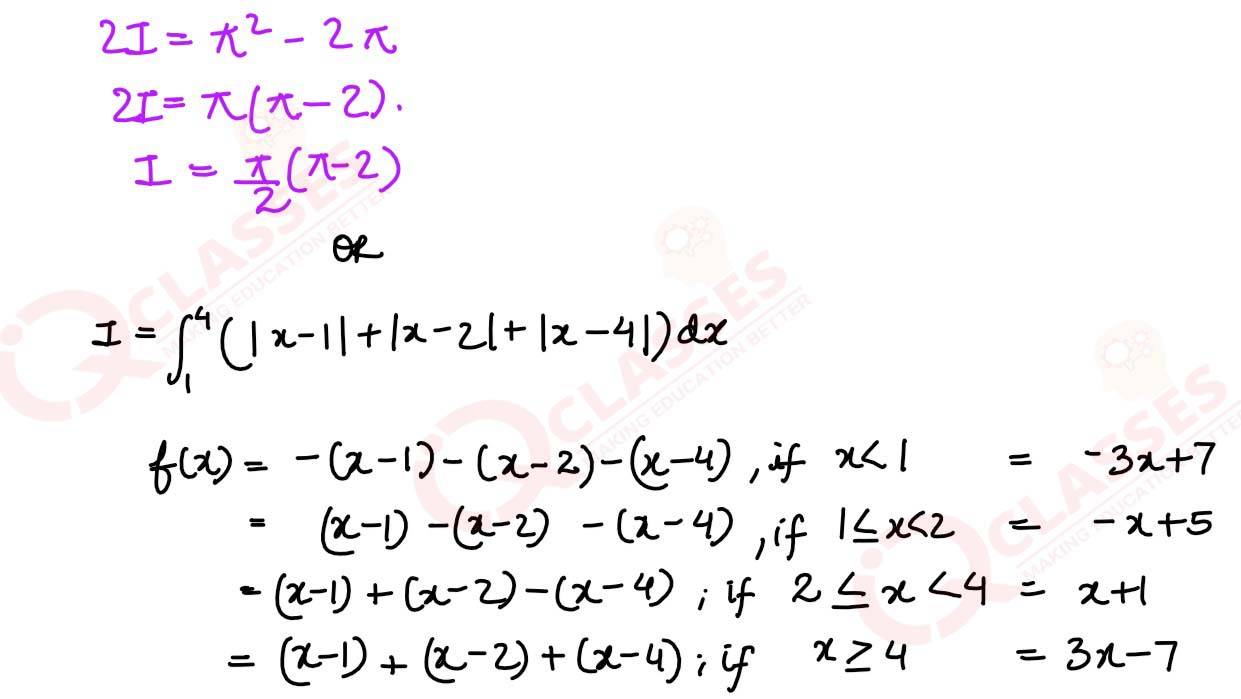

∫ 4 1 {|x-1| + |x-2| + |x-4|} dx
solutions


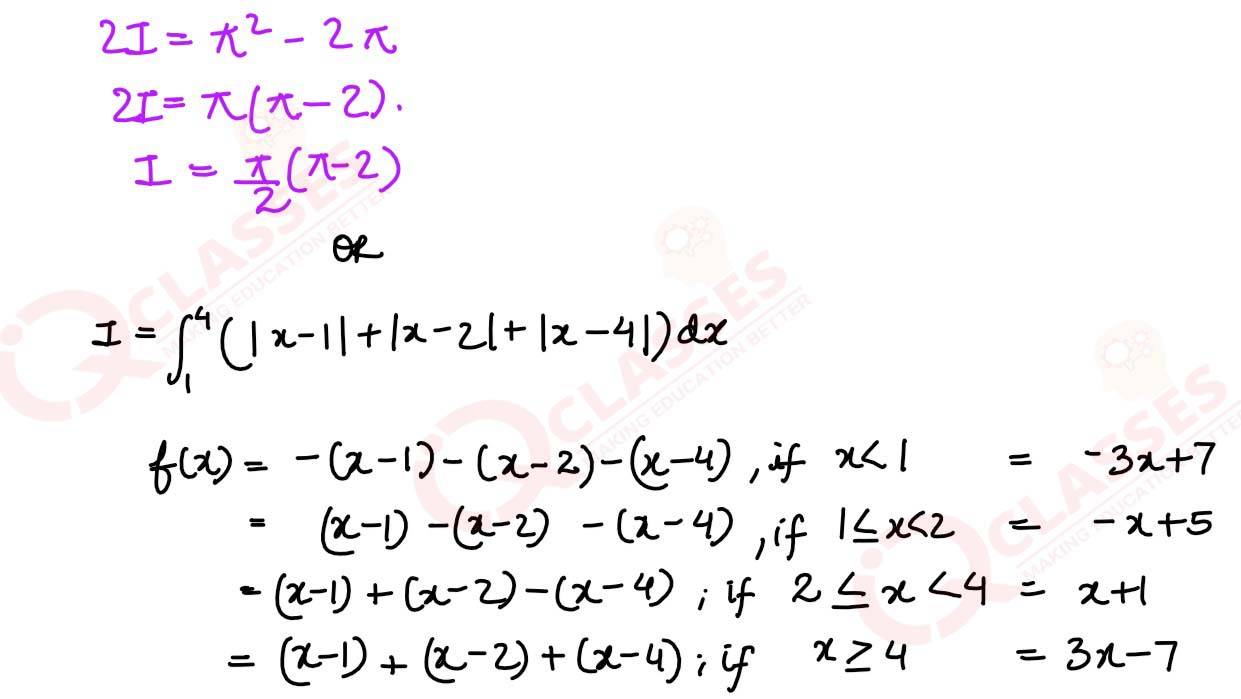

2018
Q1
Find:
∫
solutions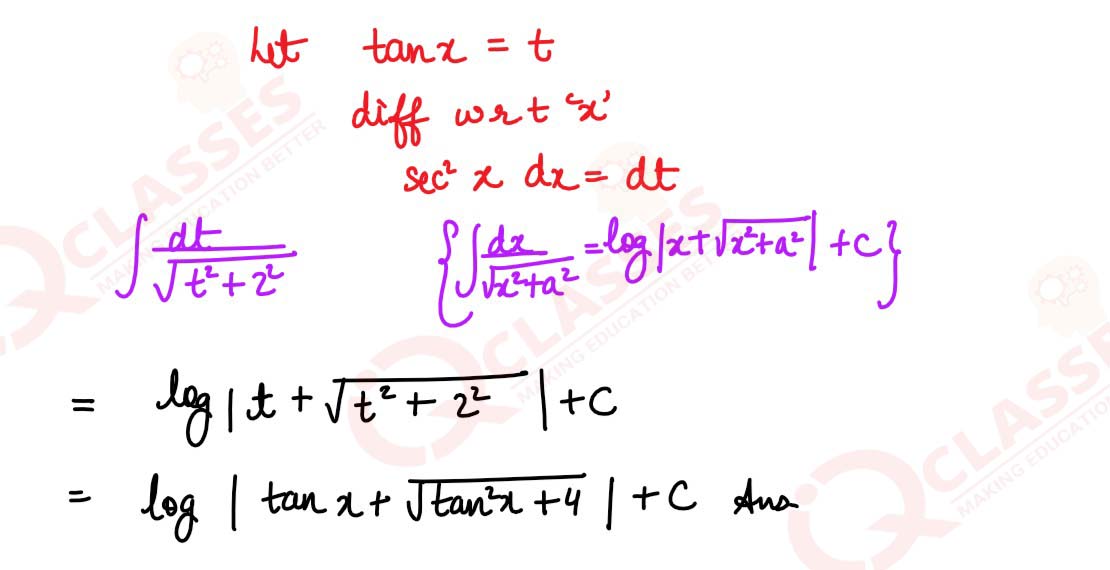
∫
sec2x
/
√tan2x +4
dx
solutions
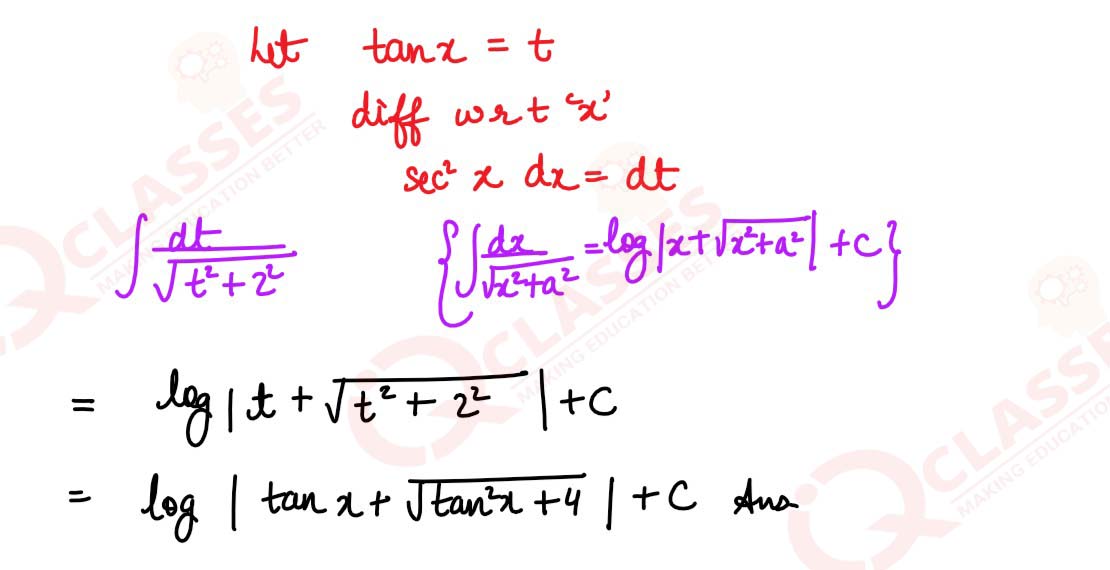
Q2
Find:
∫ √ 1-sin 2x dx,π/4 < x < π/2
OR
Find: ∫ sin-1(2x) dx
solutions
∫ √ 1-sin 2x dx,π/4 < x < π/2
OR
Find: ∫ sin-1(2x) dx
solutions

Q3
Find:
∫
solutions

3x+5
/
x2+ 3x -18
dx
solutions


Q4
Prove that
∫
a0
f(x) dx - ∫
a0 f(a-x) dx,hence evaluate
∫
π0
∫ π0 e2x.sin (π/4 + x)dx
solutions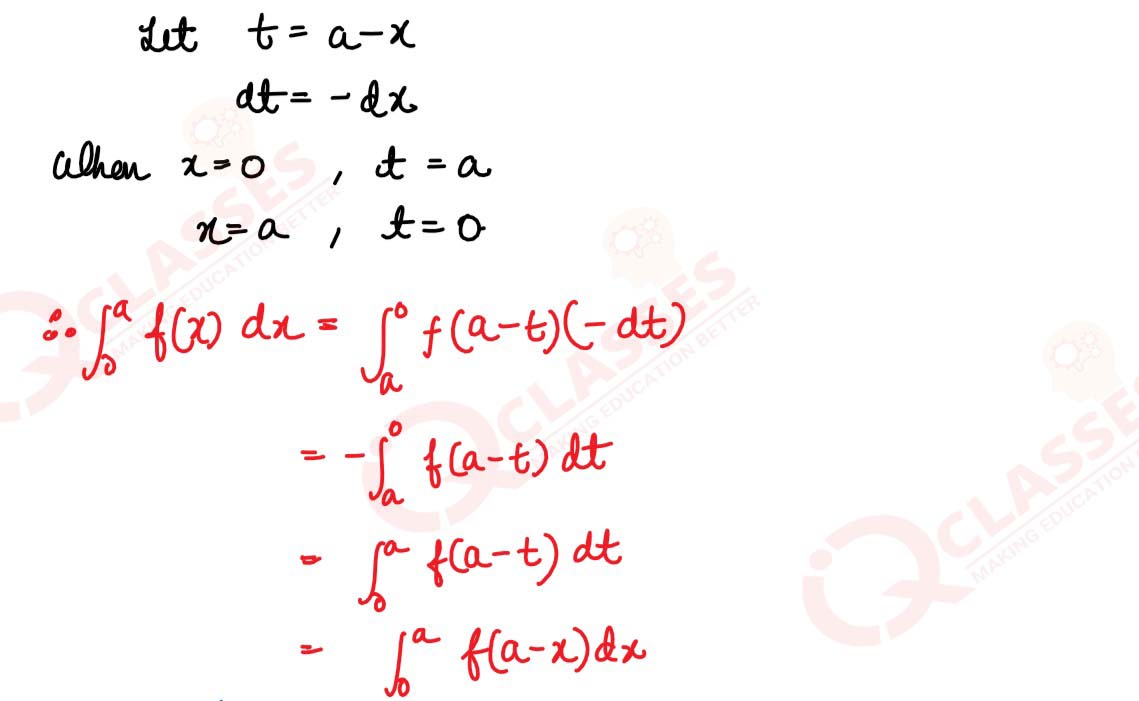


x sinx
/
1+cos2x
dx
∫ π0 e2x.sin (π/4 + x)dx
solutions
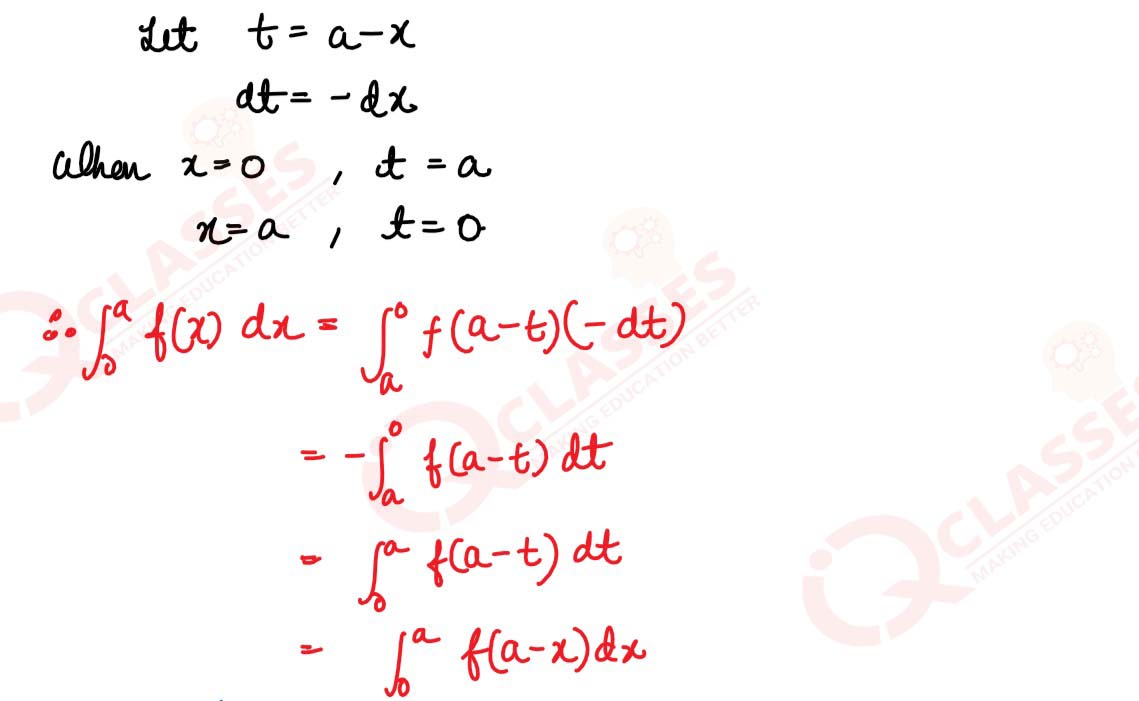


2019
Q1
Find:
∫
solutions
3-5 sinx
/
cos2x
dx
solutions

Q2
Find:
∫
solutions
4
/
(x-2)(x2+4)
dx
solutions

Q3
Evaluate:
∫
π/20
OR
∫ 31 (3x2+ 2x +1) dx has the limit of a sum
solutions

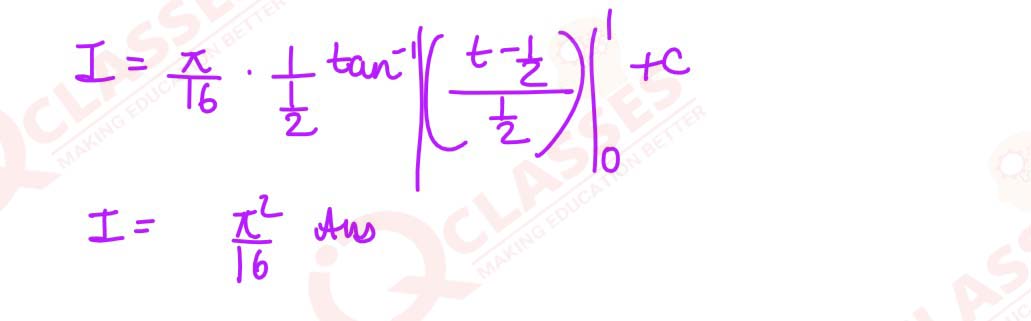
x sinx cosx
/
sin4x + cos4x
dx
OR
∫ 31 (3x2+ 2x +1) dx has the limit of a sum
solutions


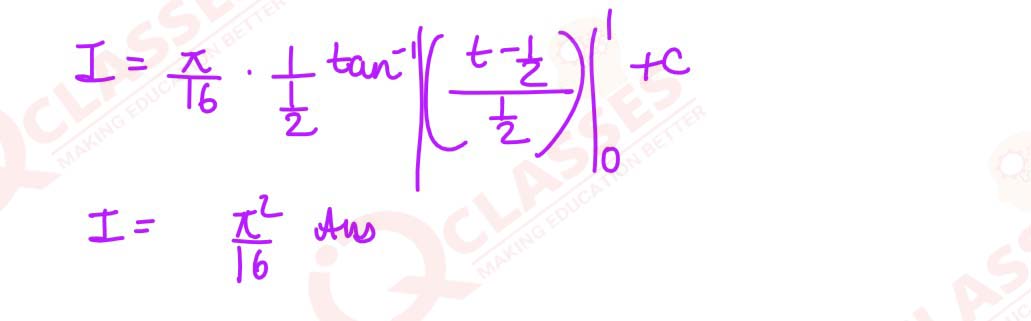
2020
Q1
Find:
∫
solutions
∫
dx
/
√ 9 - 4x2
solutions

Q2
Find:
∫ x4 logx dx
OR
Find:
solutions

∫ x4 logx dx
OR
Find:
2x
/
3√ x2+1
dx
solutions


Q3
∫
π4-π/4
sec2 x dx is equal to
(A) -1
(B) 0
(C) 1
(D) 2
solutions
(A) -1
(B) 0
(C) 1
(D) 2
solutions

Q4
Find:
∫ sec3 x dx
solutions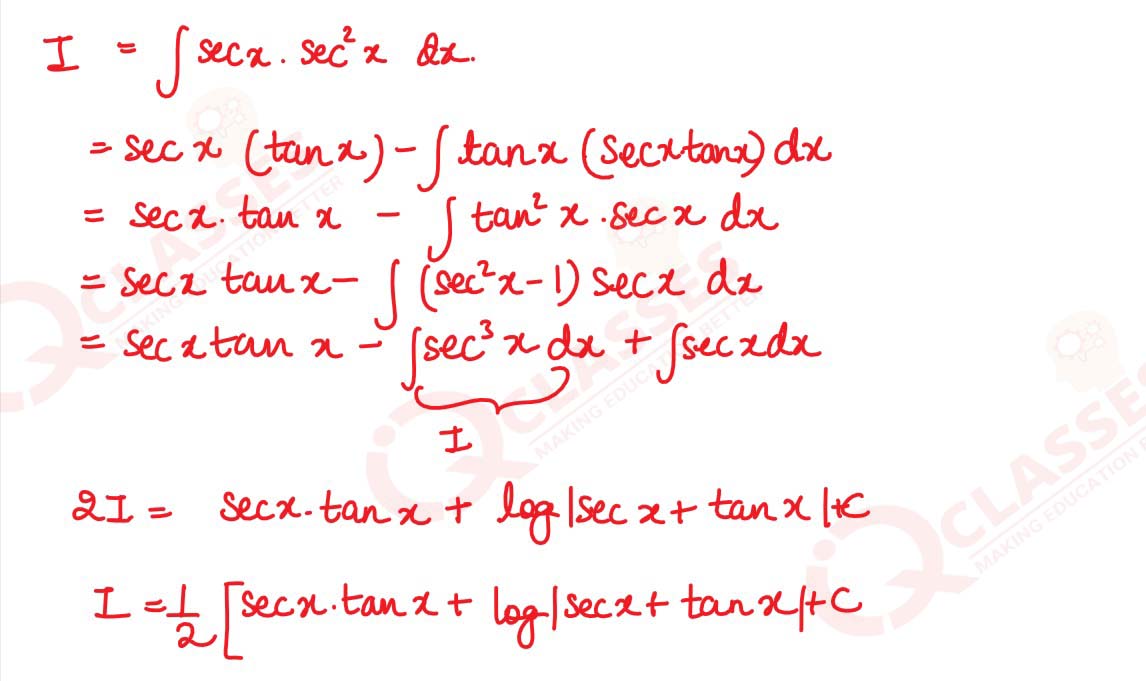
∫ sec3 x dx
solutions
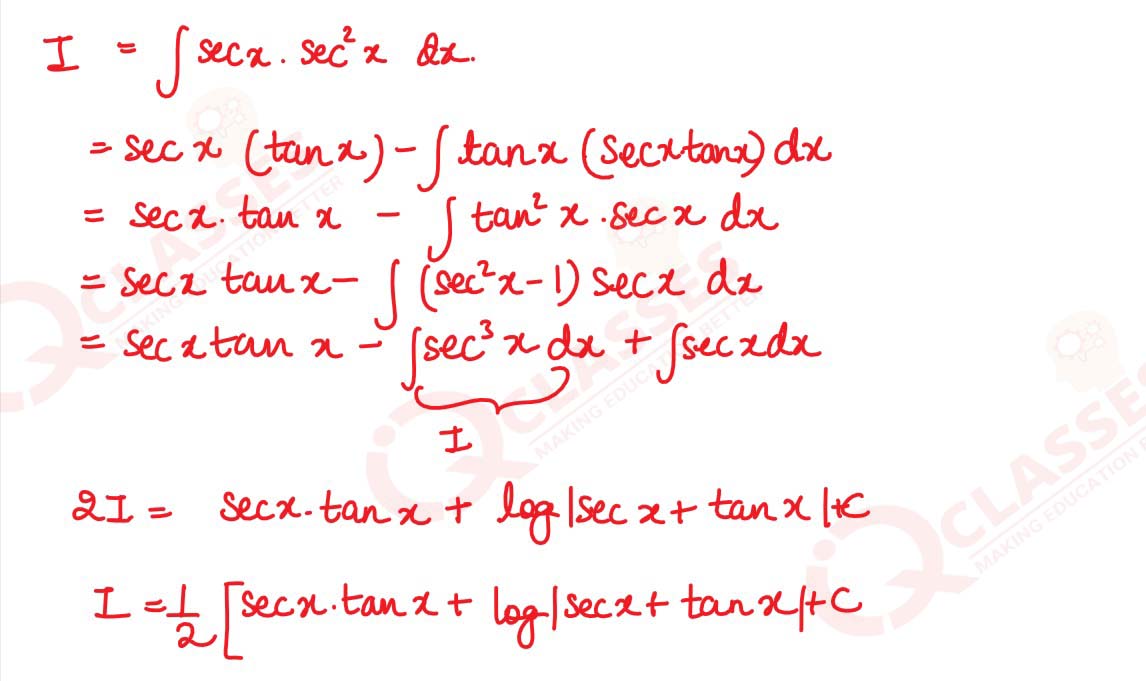


Add a comment