Class 12 Maths CBSE Probability Board Questions
Here we provide Class 12 Maths important notes,board questions and predicted questions with Answers for chapter Probability. These important notes,board questions and predicted questions are based on CBSE board curriculum and correspond to the most recent Class 12 Maths syllabus. By practising these Class 12 materials, students will be able to quickly review all of the ideas covered in the chapter and prepare for the Class 12 Board examinations.
2016
Q1
Three persons A, B and C apply for a job of Manager in a Private Company. Chances
of their selection (A, B and C) are in the ratio 1 : 2 : 4. The probabilities that A, B and
C can introduce changes to improve profits of the company are 0.8, 0.5 and 0.3
respectively. If the change does not take place, find the probability that it is due to the
appointment of C.
OR
A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins.
solutions



OR
A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins.
solutions




Q2
An urn contains 3 white and 6 red balls. Four balls are drawn one by one with
replacement from the urn. Find the probability distribution of the number of red balls
drawn. Also find mean and variance of the distribution.
solutions
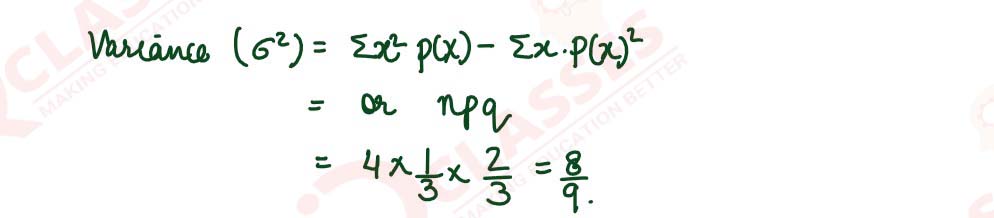
solutions

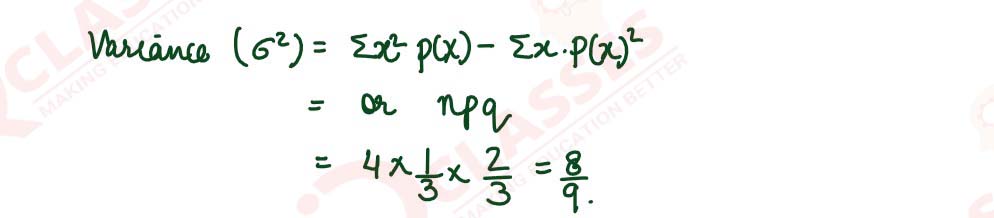
2017
Q1
A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed.
Let A be the event "number obtained is even" and B be the event
"number obtained is red". Find if A and B are independent events.
solutions
solutions

Q2
Of the students in a school, it is known that 30% have 100% attendance
and 70% students are irregular. Previous year results report that 70% of
all students who have 100% attendance attain A grade and 10% irregular
students attain A grade in their annual examination. At the end of the
year, one student is chosen at random from the school and he was found
to have an A grade. What is the probability that the student has 100%
attendance ? Is regularity required only in school ? Justify your answer.
solutions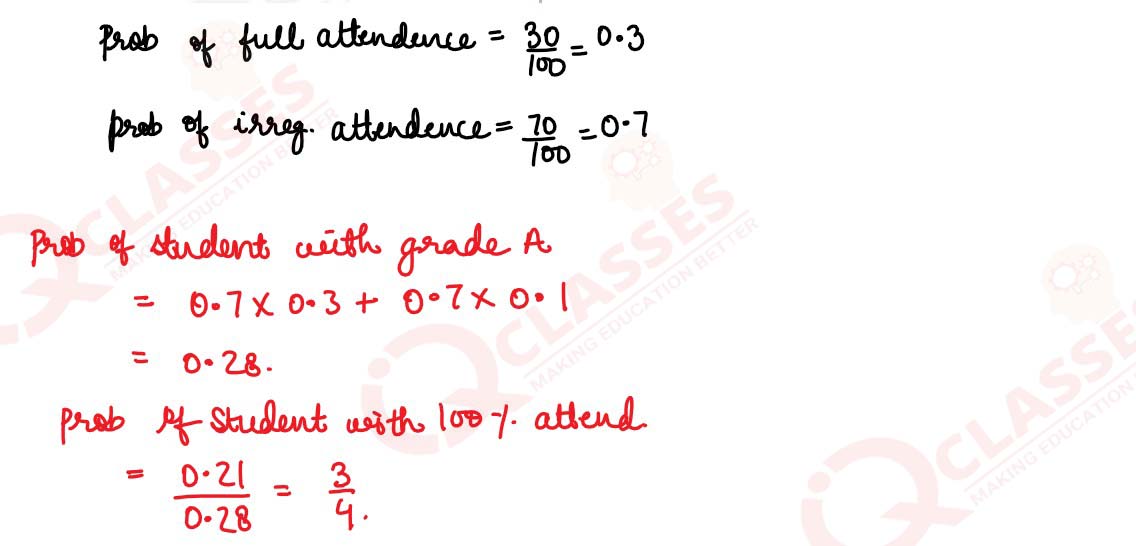
solutions
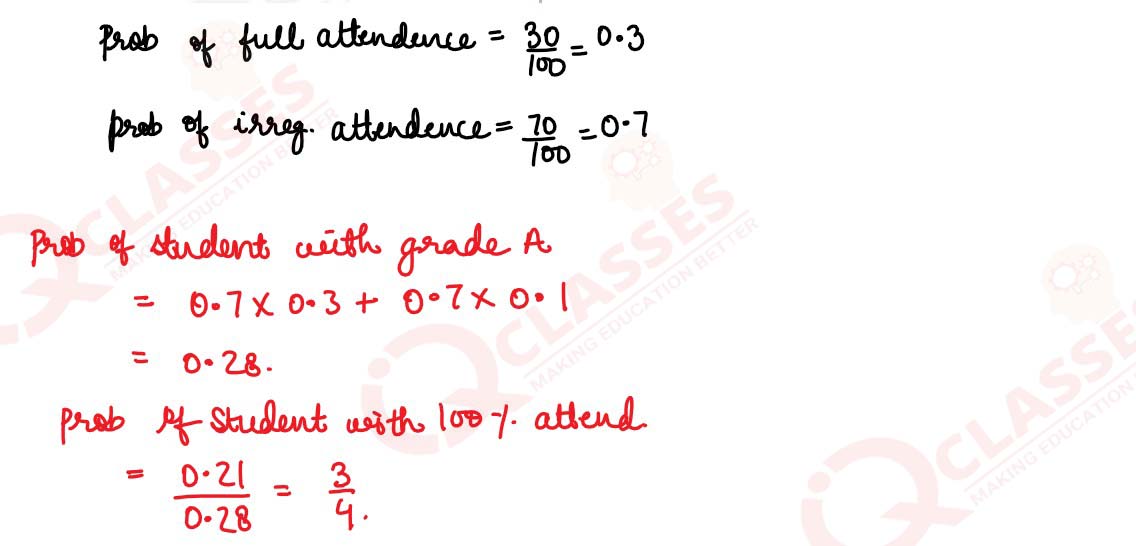
Q3
There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two
cards are drawn at random without replacement. Let X denote the sum of
the numbers on the two drawn cards. Find the mean and variance of X.
solutions
solutions

2018
Q1
A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event "number
is even" and B be the event "number is marked red". Find whether the events A and B
are independent or not.
solutions
solutions

Q2
A die is thrown 6 times. If "getting an odd number" is a "success",
probability of (i) 5 successes ? (ii) atmost 5 successes ?
OR
The random variable X has a probability distribution P(X) of the following form,where 'k' is some number.
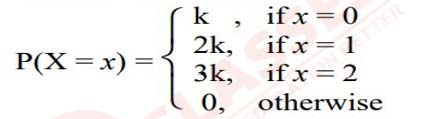
Determine the value of 'k'.
solutions

OR
The random variable X has a probability distribution P(X) of the following form,where 'k' is some number.
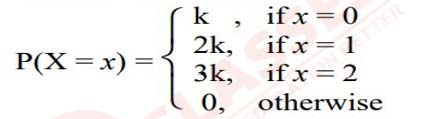
Determine the value of 'k'.
solutions


Q3
A manufacturer has three machine operators A, B and C. The first operator A produces
1% of defective items, whereas the other two operators B and C produces 5% and 7%
defective items respectively. A is on the job for 50% of the time, B on the job 30% of
the time and C on the job for 20% of the time. All the items are put into one stockpile
and then one item is chosen at random from this and is found to be defective. What is
the probability that it was produced by A ?
solutions
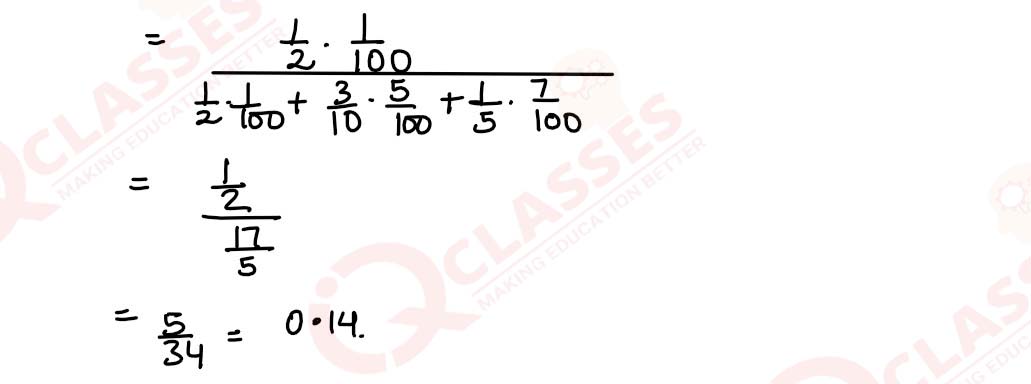
solutions

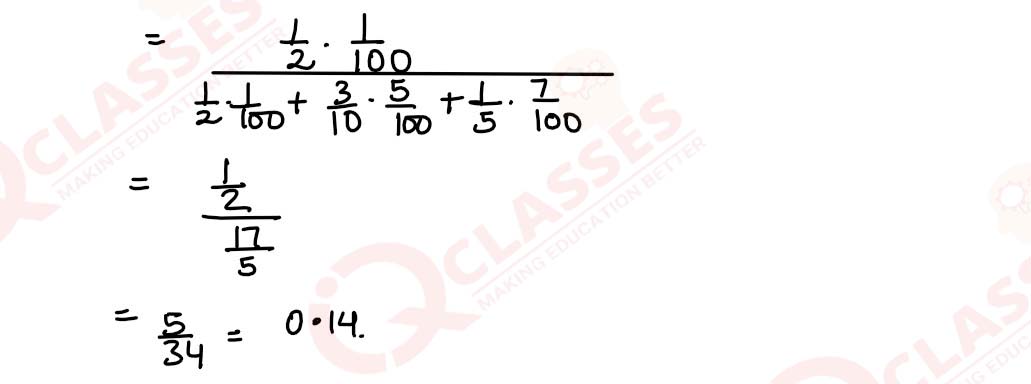
2019
Q1
Evaluate P(A U B), if 2P(A)=P(B)=5/13 and P(A/B) =2/5
solutions

solutions


Q2
Two groups are competing for the positions of the Board of Directors of a corporation.
The probabilities that the first and second groups will win are 0.6 and 0.4 respectively.
Further, if the first group wins, the probability of introducing a new product is 0.7 and
the corresponding probability is 0.3 if the second group wins. Find the probability that
the new product introduced was by the second group.
solutions

solutions


Q3
From a lot of 20 bulbs which include 5 defectives, a sample of 3 bulbs is drawn at
random, one by one with replacement. Find the probability distribution of the number
of defective bulbs. Also, find the mean of the distribution.
solutions

solutions


2020
Q1
If A and B are two independent events with P(A) = 1/3
P(B)=1/4, then P(B' | A) is equal to
(A) 1/4
(B) 1/3
(C) 3/4
(D) 1
solutions
(A) 1/4
(B) 1/3
(C) 3/4
(D) 1
solutions

Q2
Two cards are drawn at random and one-by-one without replacement
from a well-shuffled pack of 52 playing cards. Find the probability that
one card is red and the other is black.
solutions
solutions

Q3
The probability of finding a green signal on a busy crossing X is 30%.
What is the probability of finding a green signal on X on two consecutive
days out of three ?
solutions
solutions

Q4
There are two bags, I and Il. Bag I contains 3 red and 5 black balls and
Bag Il contains 4 red and 3 black balls. One ball is transferred randomly
from Bag I to Bag Il and then a ball is drawn randomly from Bag Il. If
the ball so drawn is found to be black in colour, then find the probability
that the transferred ball is also black.
OR
An urn contains 5 red, 2 white and 3 black balls. one-by-one, at random without replacement.Find the probability distribution of the number of white balls. Also, find the mean and the variance of the number of white balls drawn. Three balls are drawn
solutions
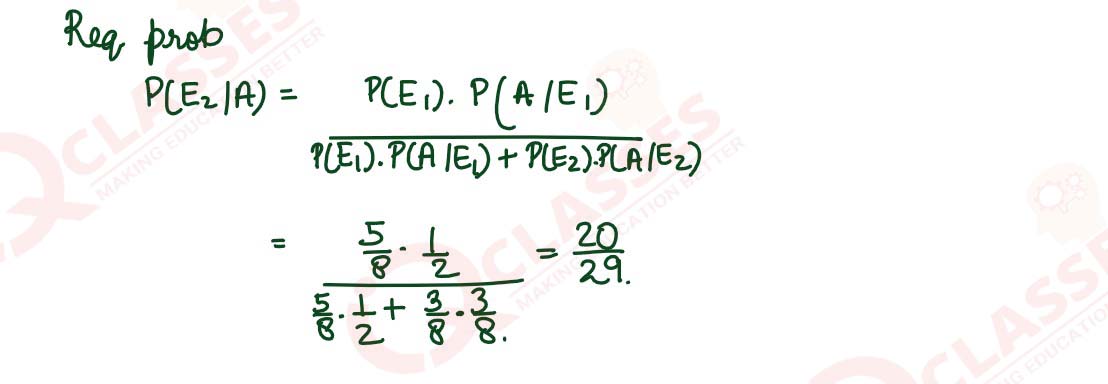
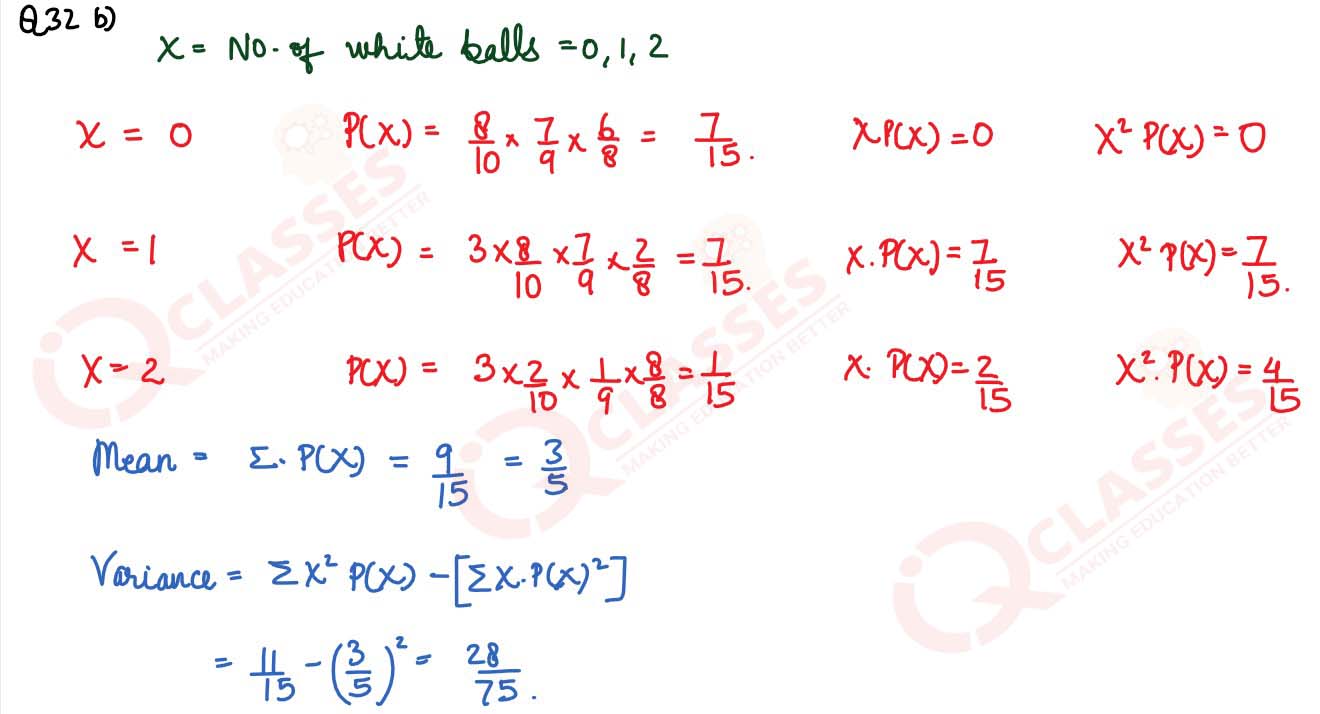
OR
An urn contains 5 red, 2 white and 3 black balls. one-by-one, at random without replacement.Find the probability distribution of the number of white balls. Also, find the mean and the variance of the number of white balls drawn. Three balls are drawn
solutions

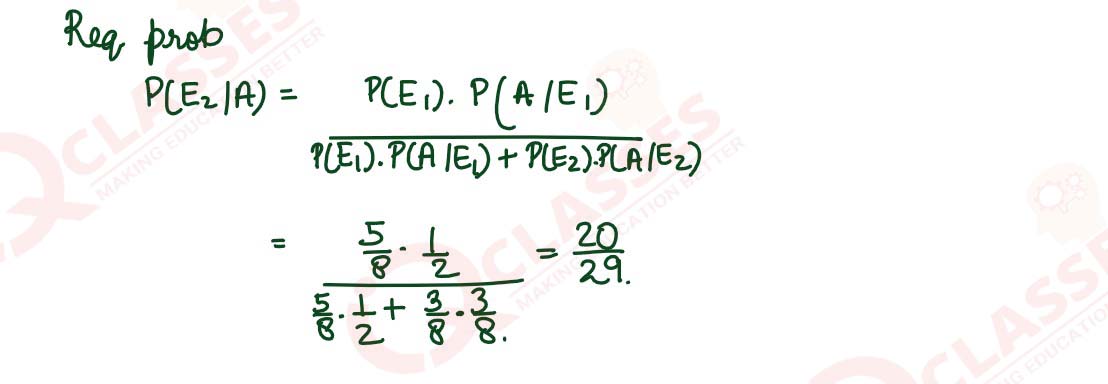
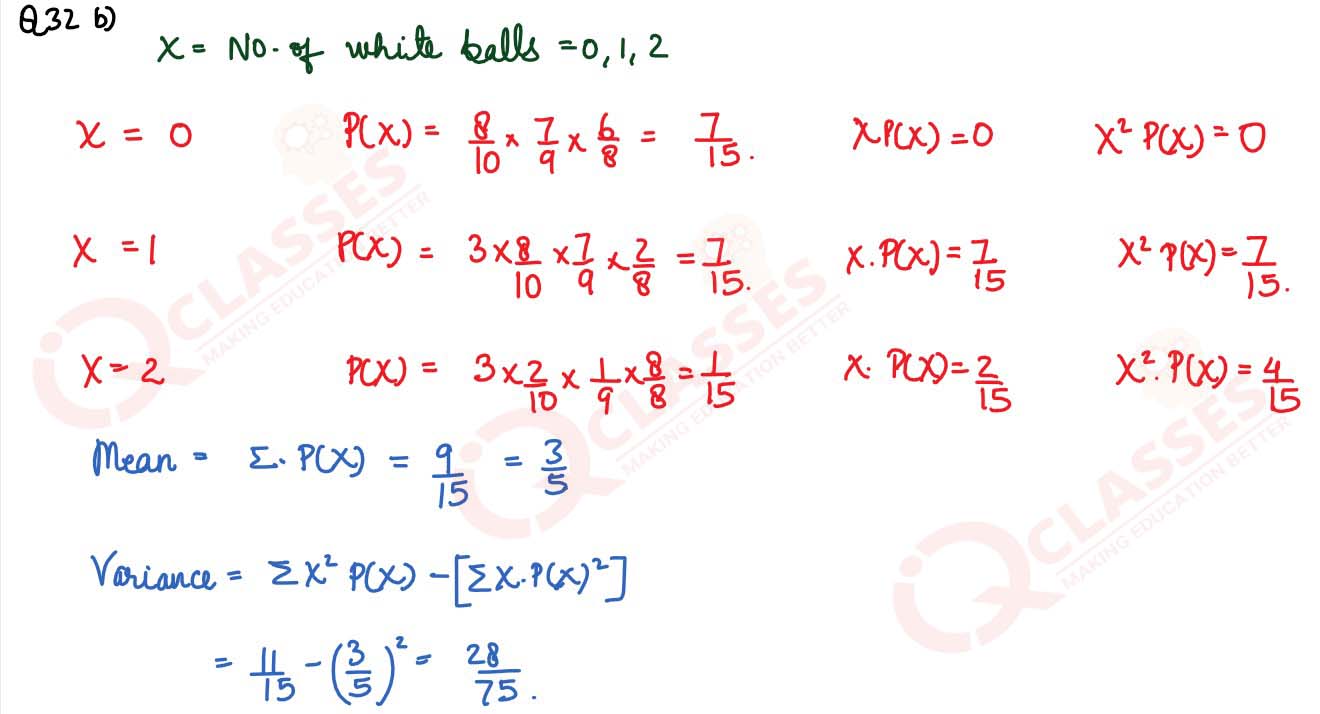

Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment