Class 12 CBSE Application of Integrals Important Questions
Integrals are mainly used for calculating the area between simple curves or between lines, parabolas,
and ellipses. Integration can also be used for calculating the average value of a function, for example,
the average rainfall per day can be recorded using Integrals.
Integrals can also be applied to find the area between two curves. Here, the area can be calculated by
splitting the regions under the curve into a number of smaller areas and they can be added at last for
finding the total area under the curve.
Q1 Draw a rough sketch of the curve x2 + y = 9 and find the area enclosed by the curve, the x-axis and the lines x + 1 = 0 and x — 2 = 0.
Solution
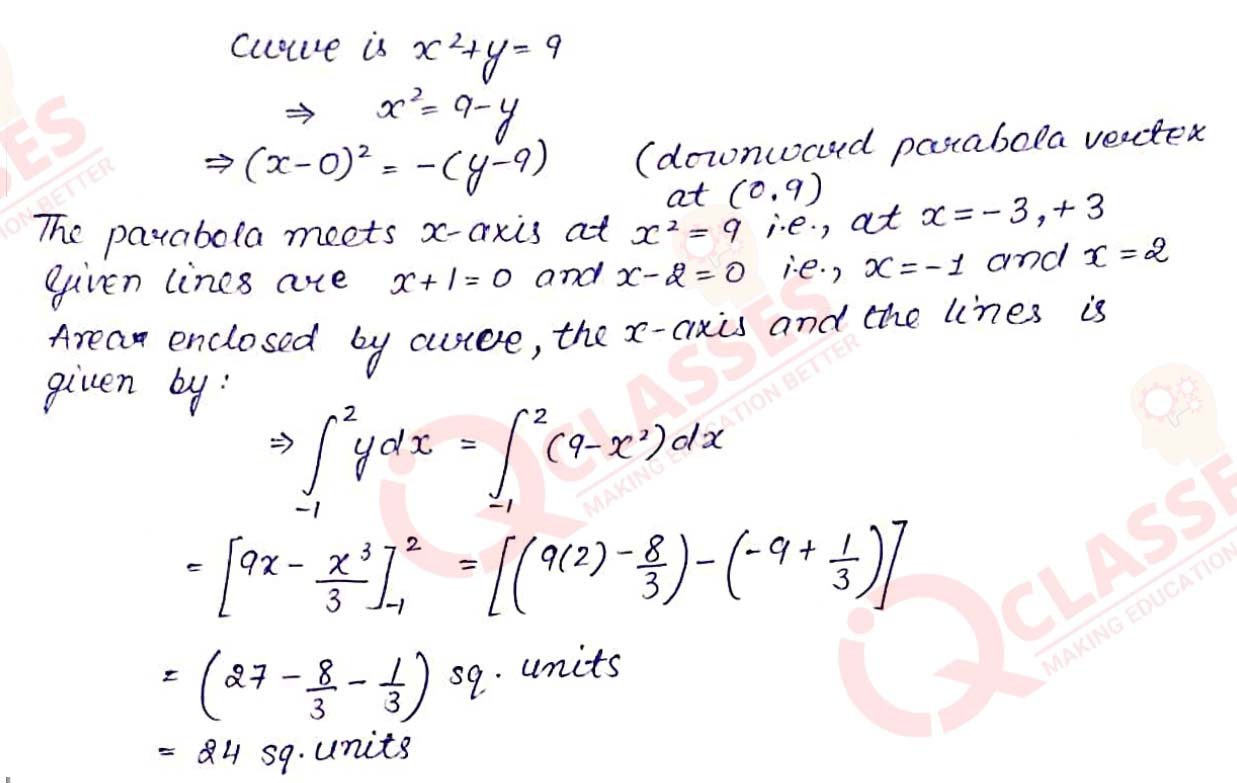
Q2 Find the well of the region bounded by the curve x = 4y - y2 and the y-axis
Solution
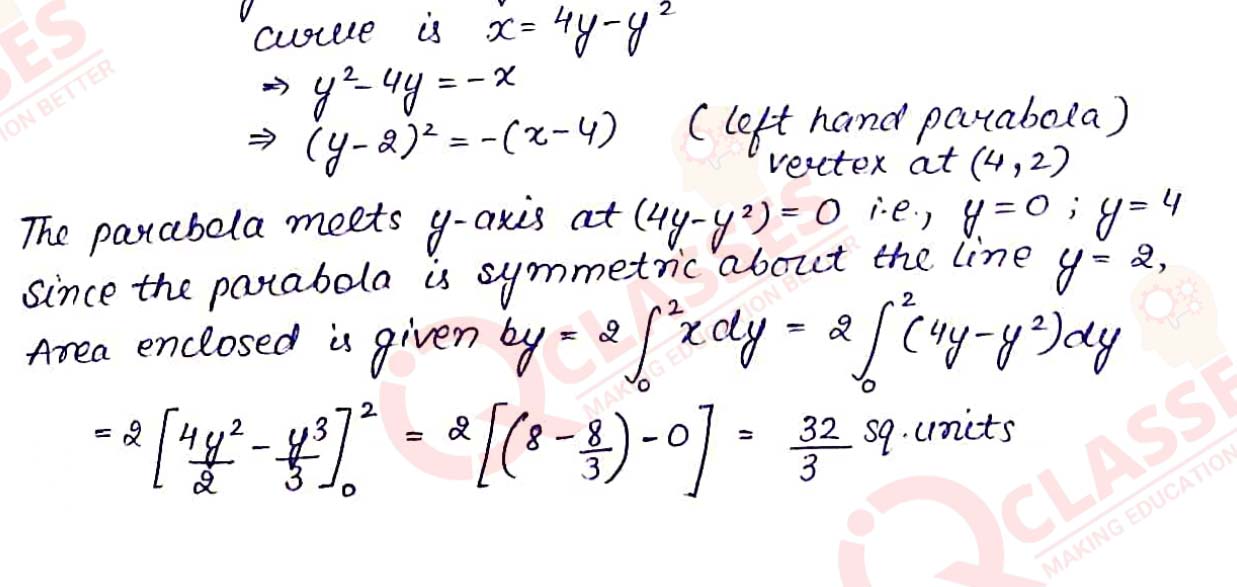
Q3 Draw a rough sketch of the curve y = x2 - 5x + 6 and find the area bounded by the curve and the x-axis.
Solution

Q4 Find the area bounded by the ellipse x2⁄a2 + y2⁄b2= 1 and the ordinates x = 0 and x = ae where b2 = a2(1-e2) and 0 < e < 1
Solution

Q5 The area between x = y2 and x =4 is divided into two equal parts by the line x = a, find he value of a.
Solution

Q6 If the area bounded by the parabola y2 = 16ax and the line y = 4 mx is a2⁄ 12 sq. units, using integration, find the value of m.
Solution

Q7 Find the area of the smaller region bounded by the ellipse x2⁄a2 + y2⁄b2 = 1 and the straight line x⁄a + y⁄b = 1
Solution

Q8 Find the area bounded by the curve y = √x and the line x = 2y + 3 in the first quadrant and the x - axis.
Solution

Q9 Find teh area of the region bounded by the parabolas y2 = 4ax and x2 = 4ay, a > 0
Solution

Q10 Find the area of the region bounded by the curve y = 6x - x2 and y = x2 - 2x
Solution

Q11 Find the area of the region bounded by the curve y2 = 4x, y-axis and he line y = 3.
Solution
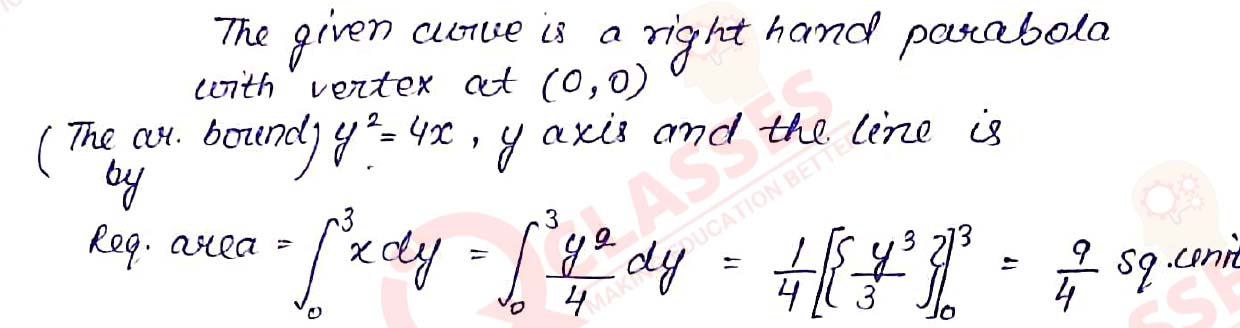
Q12 Find the area of the region in the first quadrant enclosed by the x-axis, the line x = √y and the circle x2 + y 2 = 4
Solution

Q13 Using integration, find the area of the region bounded by the following curves, after making a rough sketch. y = 1 + |x + 1|, x = -3, x =3 , y = 0
Solution

Q14 Using integration, find the area bounded by the curves y = |x - 1| and y = 3 - |x|.
Solution

Q15 The ratio of the 11th term to the 18th term of an A.P. is 2 : 3. Find the ratio of the 5th term to the 21st term, and also the ratio of the sum of first five terms to the sum of first 21 terms.
Solution



Add a comment