Class 12 CBSE Inverse Trigonometric Functions Important Questions
Inverse Trigonometric Functions for Class 12 includes the major concepts related to the inverse of trigonometric functions, which will help the students score good marks in their examinations. The inverse trigonometric functions play an essential role in calculus, for they serve to define many integrals. The concepts of inverse trigonometric functions are also used in science and engineering.
class 12 CBSE Inverse Trignometric Functions ImportantQuestions
Inverse Trigonometric Functions ImportantQues
Q1
cot-1
(- 
1
/
√3
)
Solution

Q2
sec-1
(- 
2
/
√3
)
Solution

Q3
sin-1(-1)
Solution
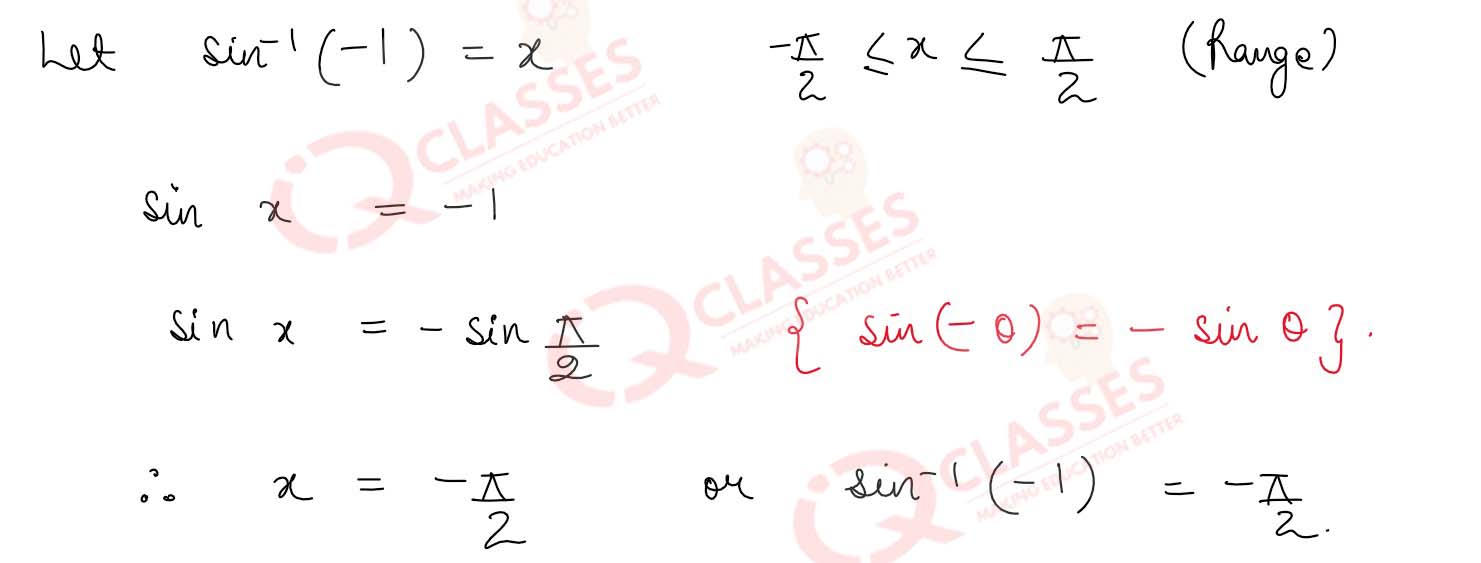
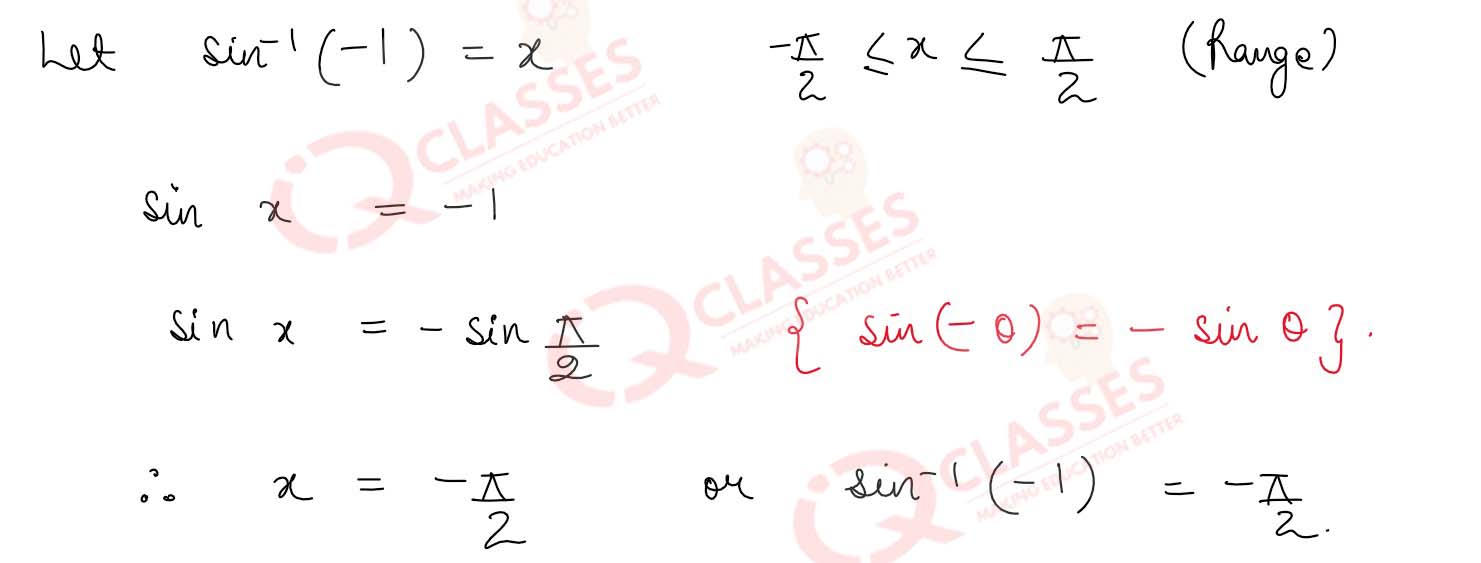
Q4
cos-1
(cos 

4π
/
3
)
Solution


Q5
sin-1
(sin 
2π
/
3
)
Solution

Q6
tan-1
(tan 

3π
/
4
)
Solution


Q7
tan-1
(tan 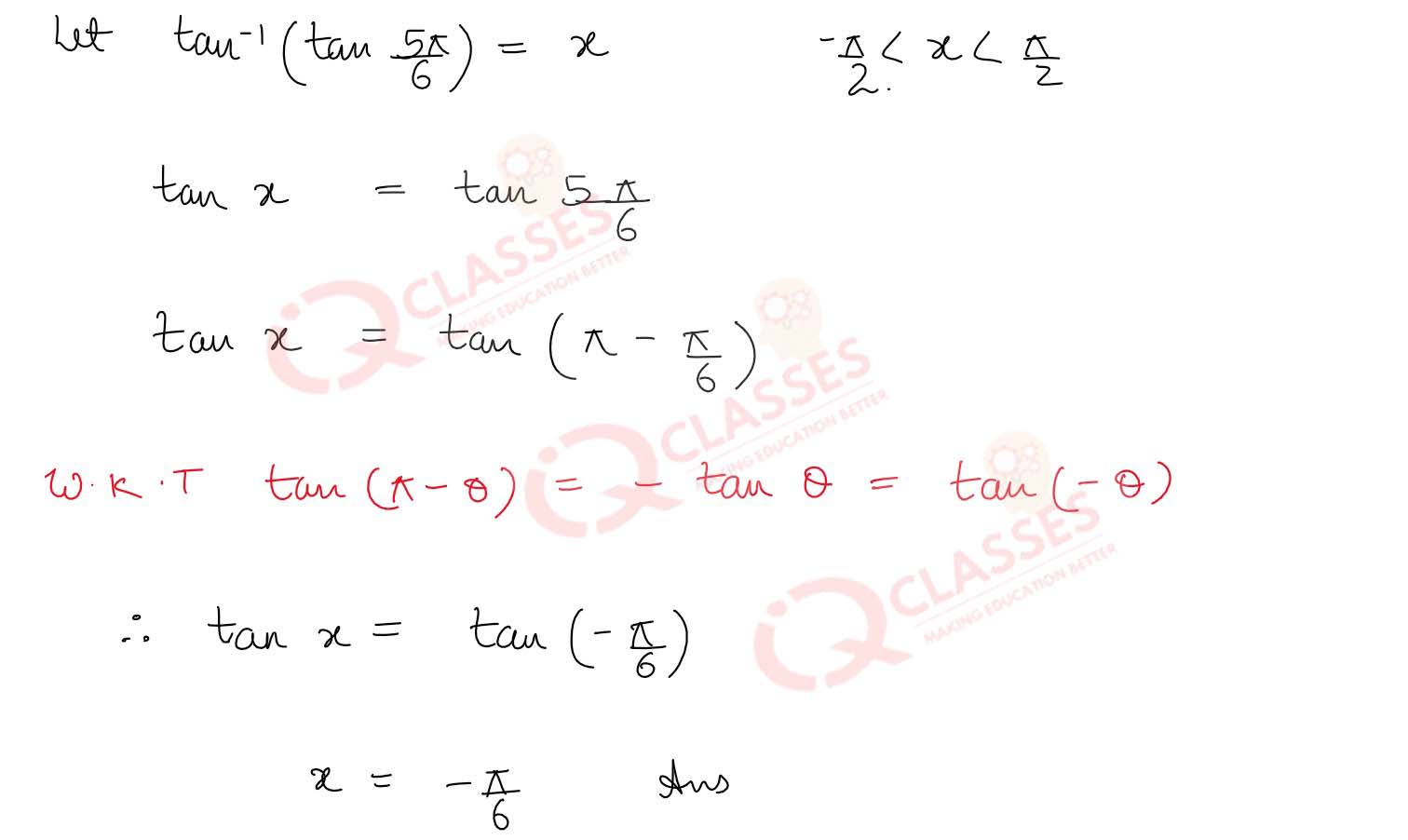
5π
/
6
) ≠
5π
/
6
, What is its value
Solution
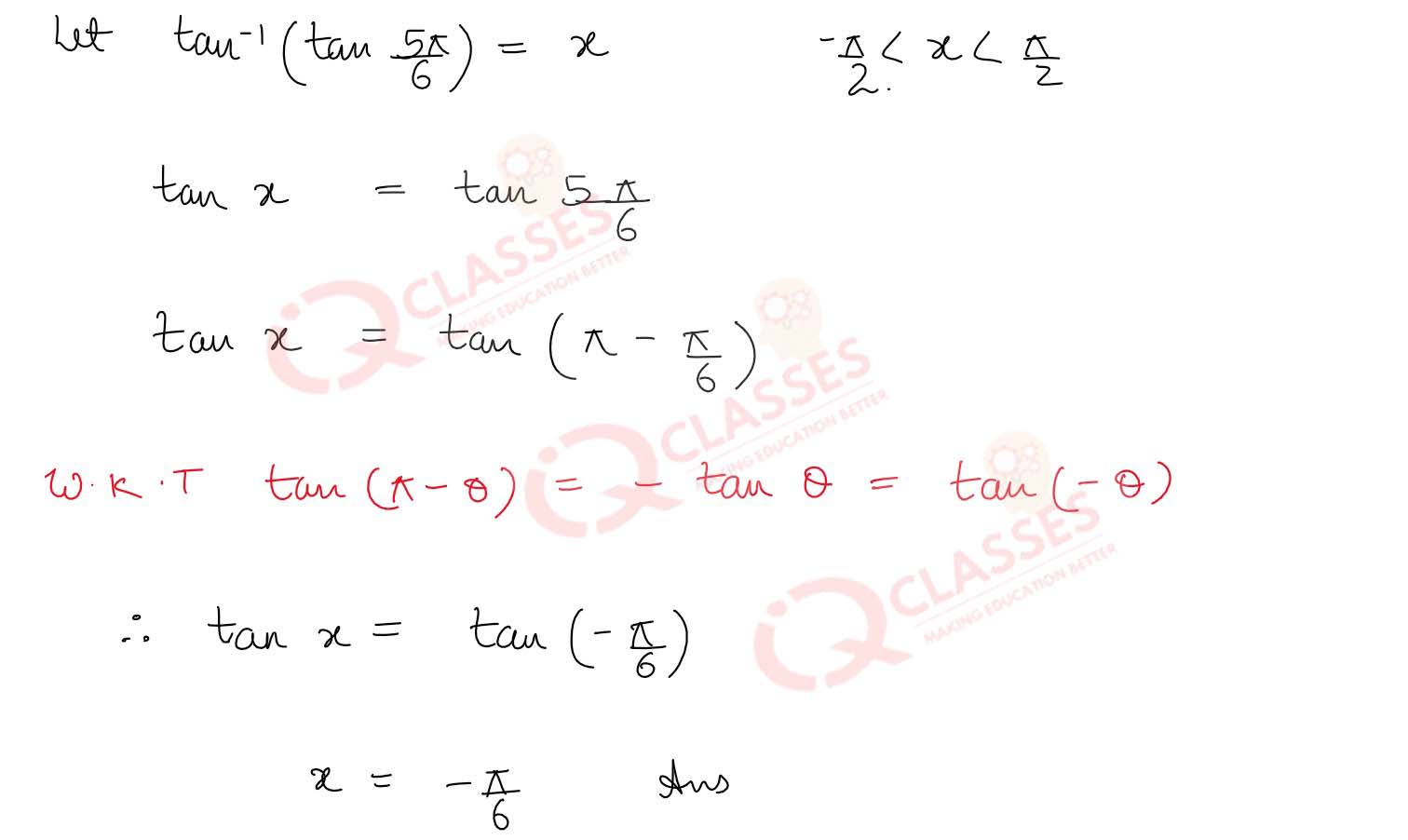
Q8
sin-1
(sin 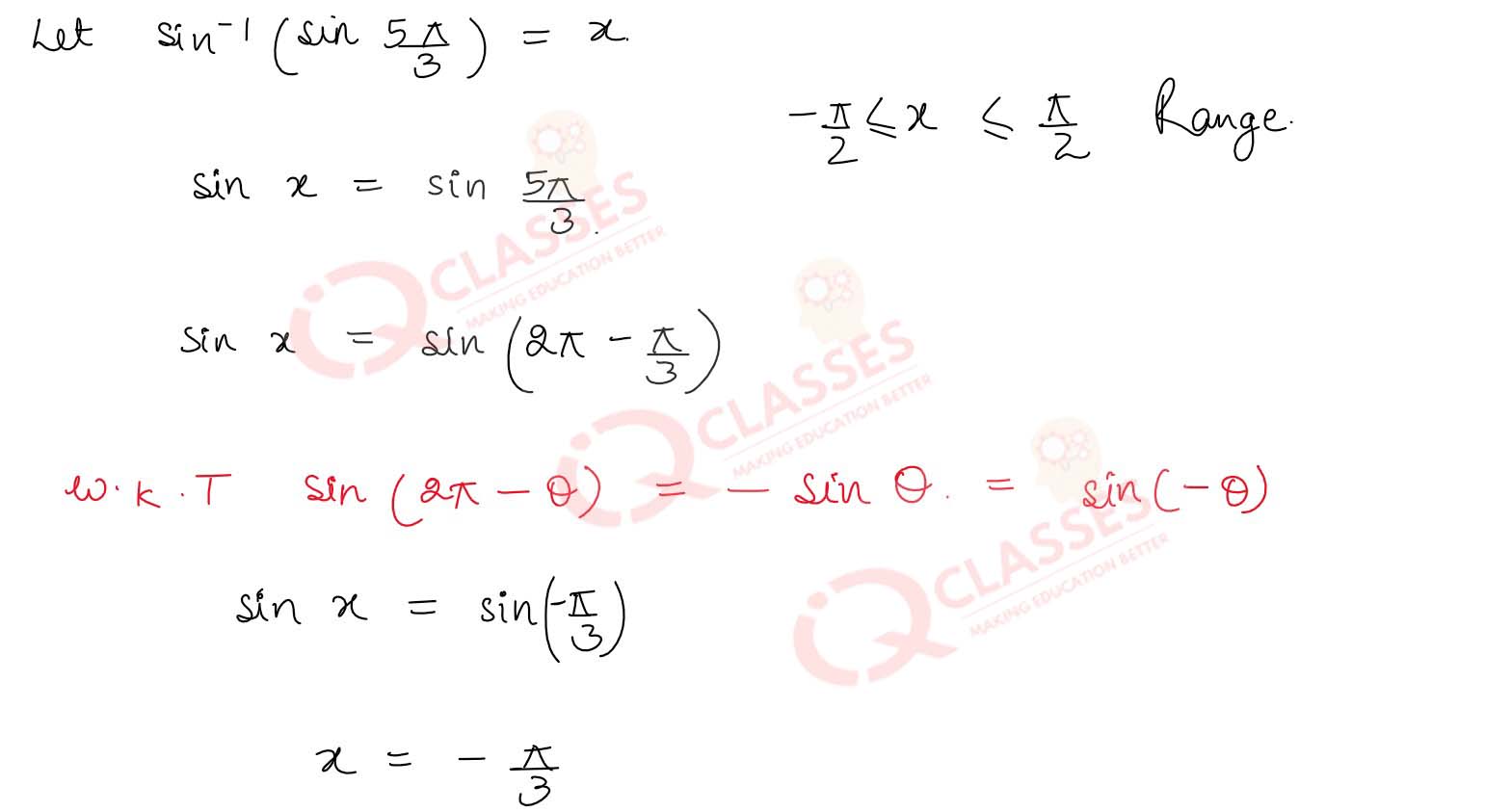
5π
/
3
) ≠
5π
/
3
, What is its value
Solution
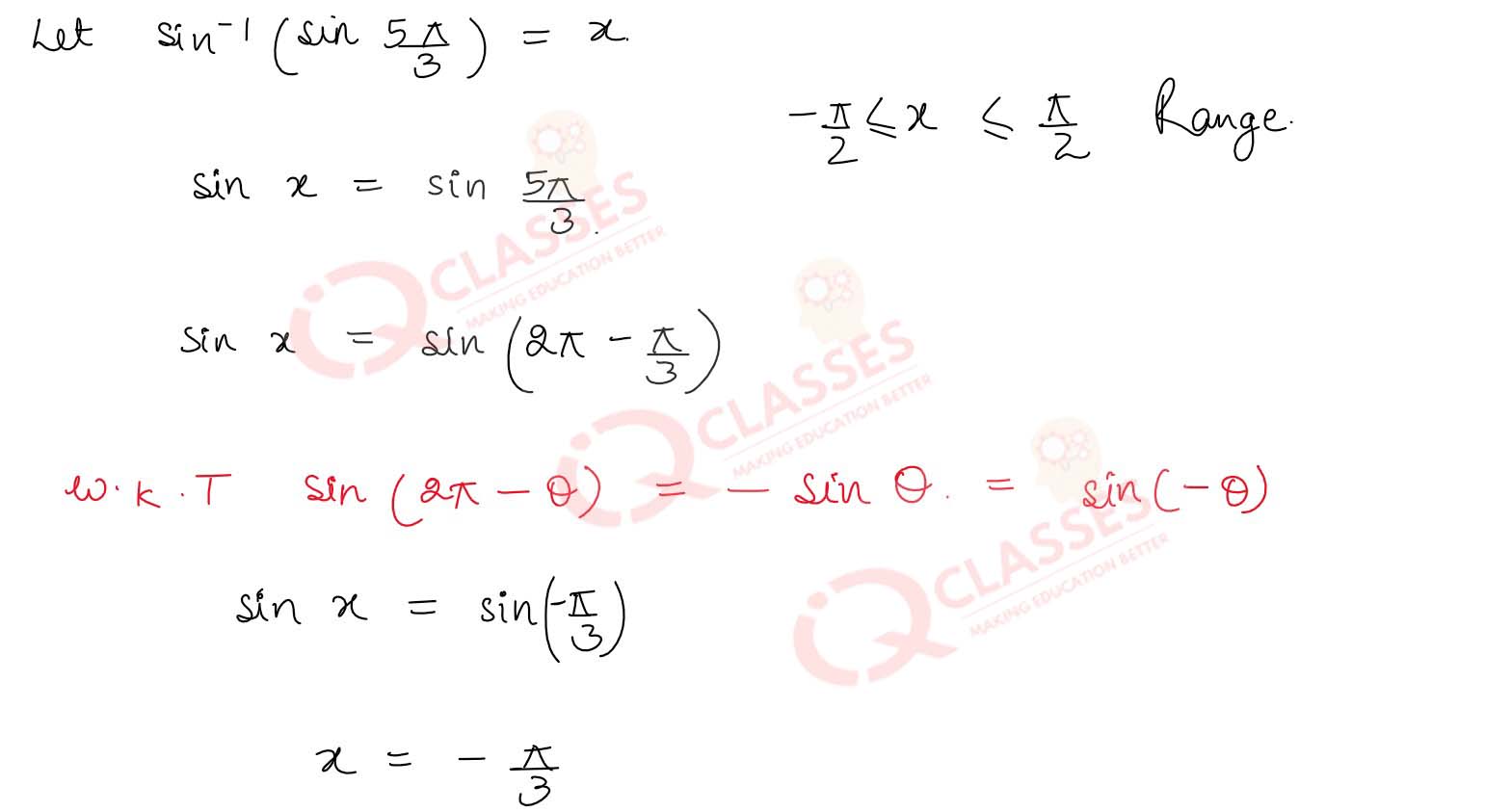
Q9
Find the domain of sin-1 ( 1 - x)
Solution


Q10
Find the domain of sec-1 (2x - 3)
Solution


Q11
sin
(2 sin -1

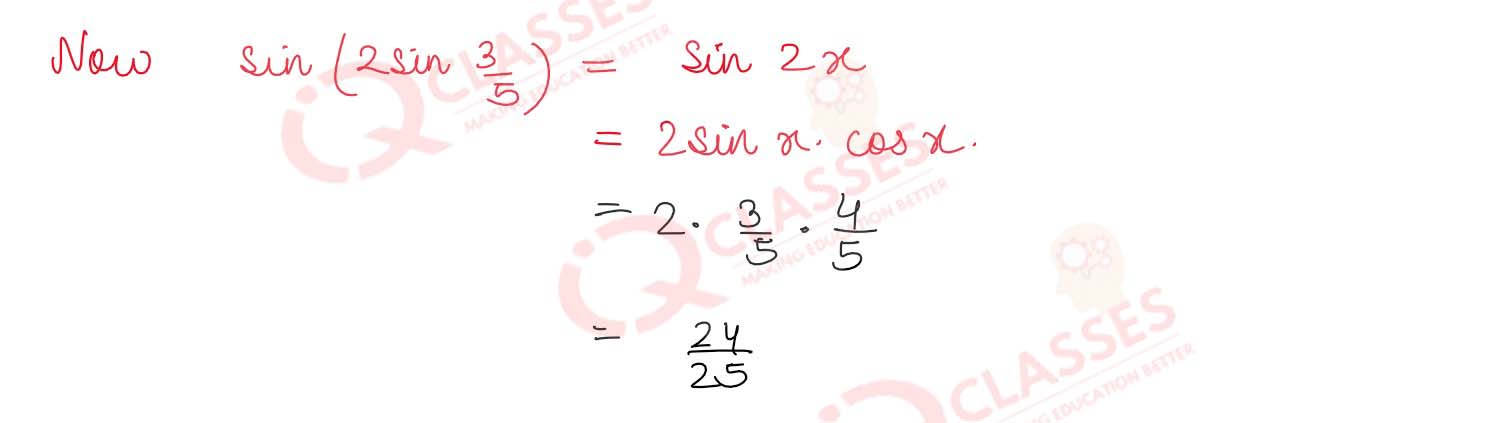
3
/
5
)
Solution

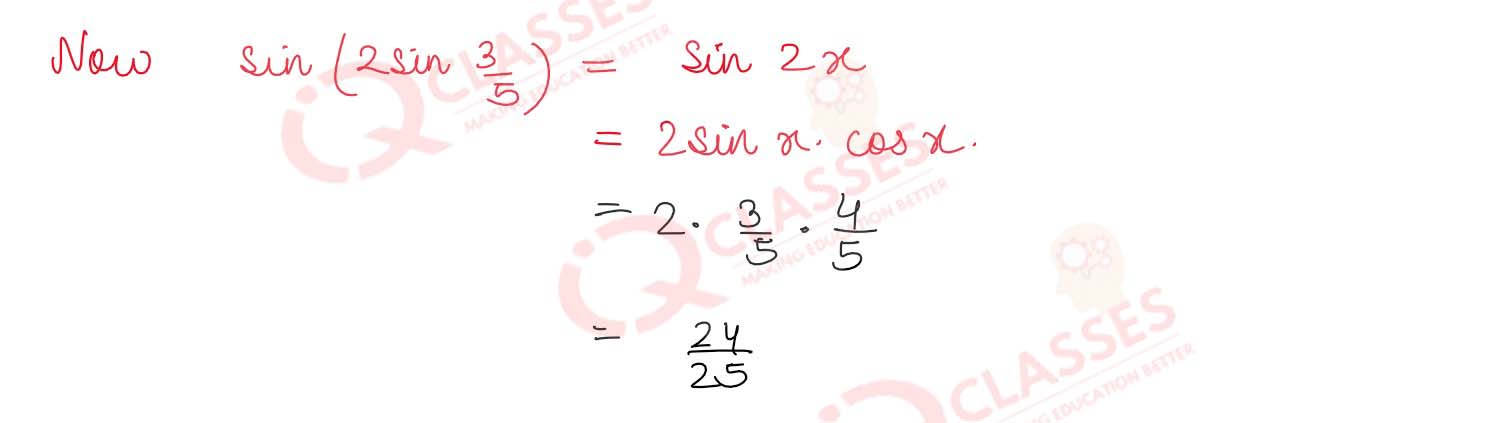
Q12
sin
(2 cos -1(- 
3
/
5
))
Solution

Q13
sin
(2 cot -1(- 
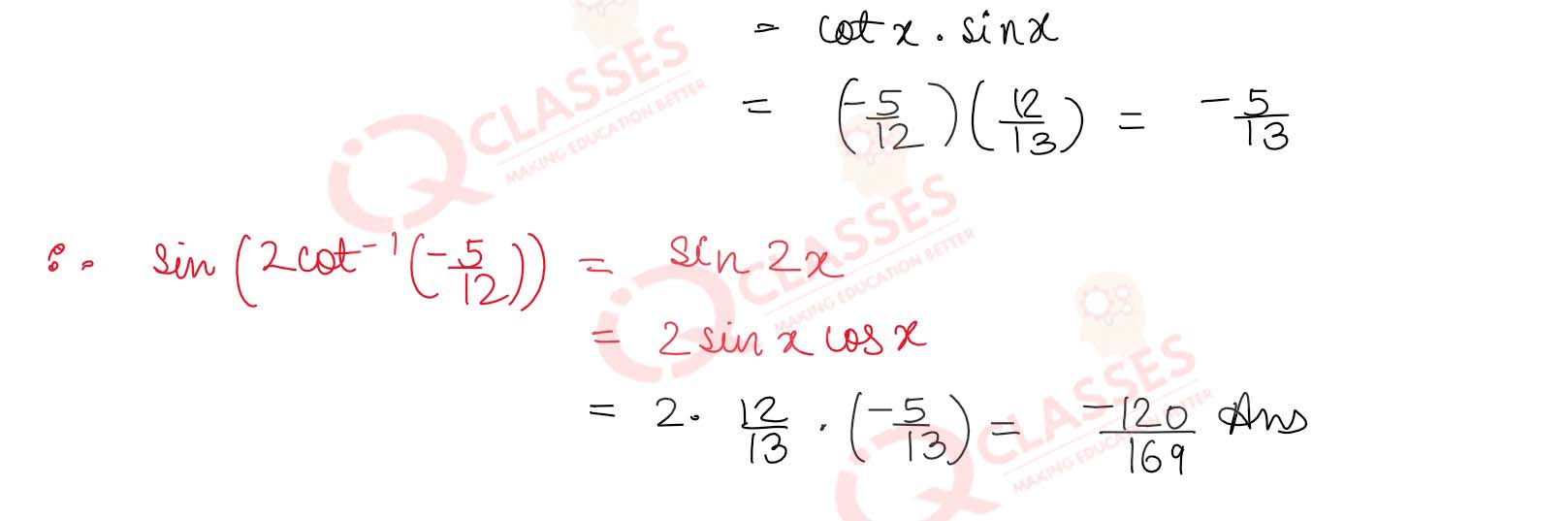
5
/
12
))
Solution

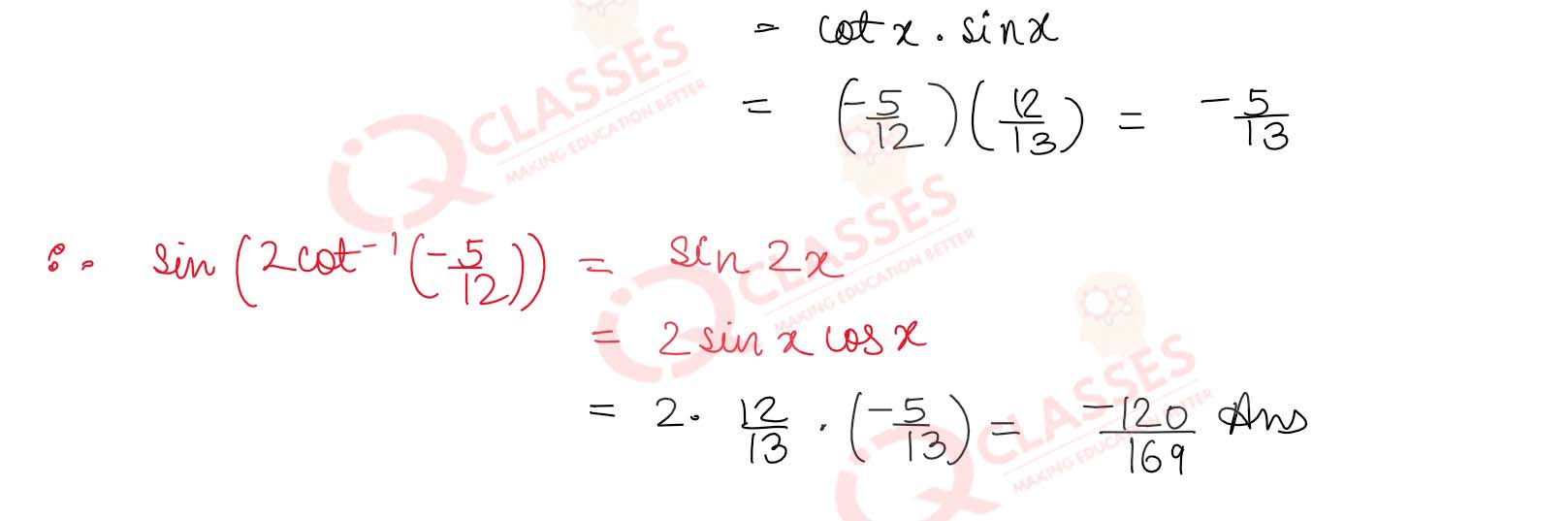
Q14
tan-1
(tan 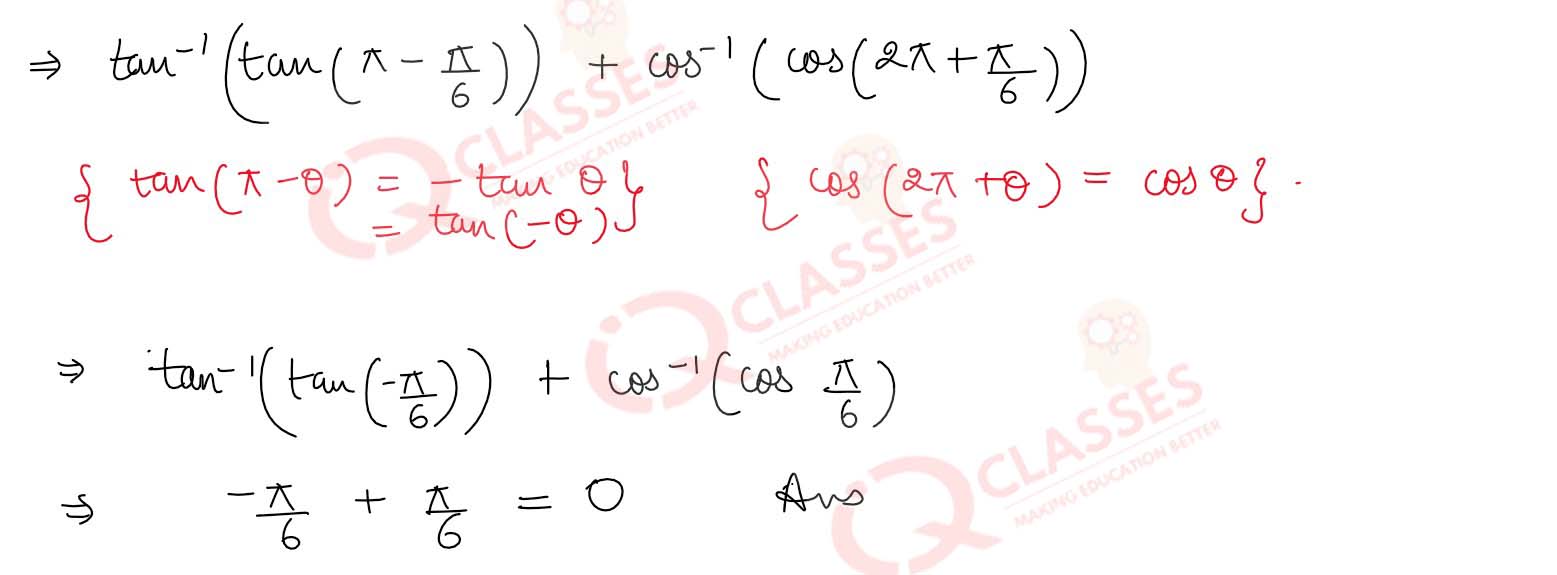
5π
/
6
) + cos-1
(cos
13π
/
6
)
Solution
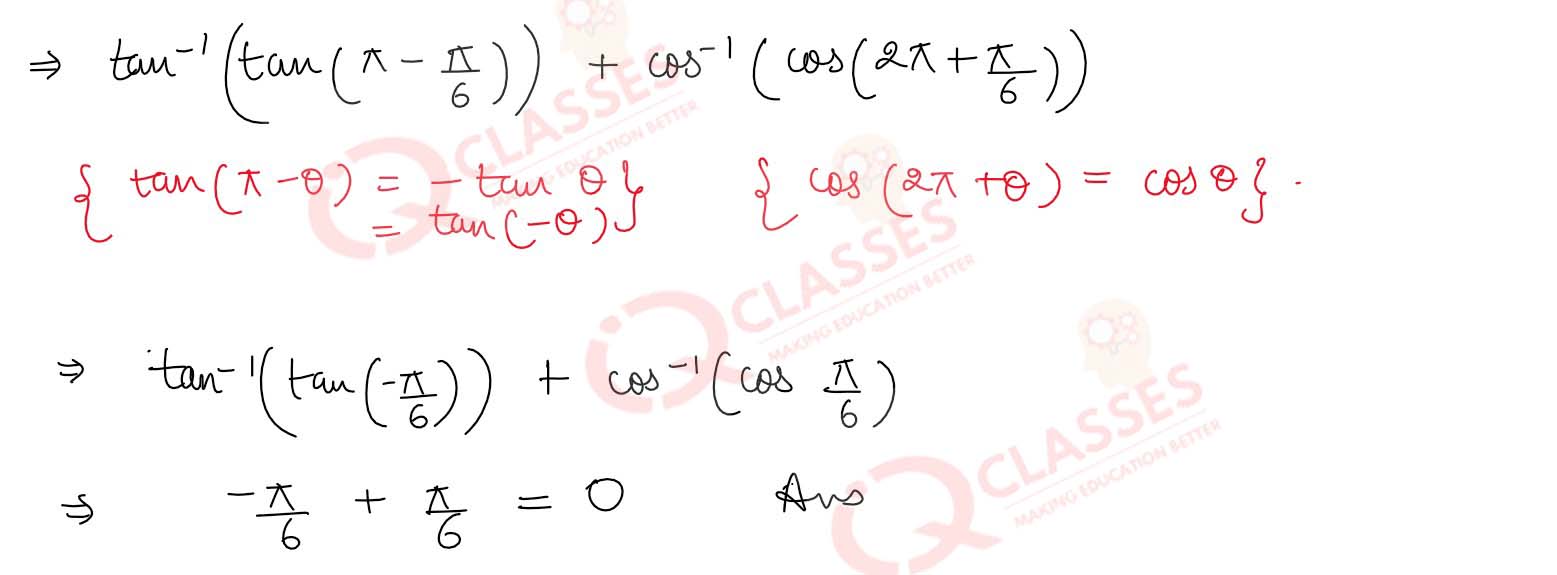
Q15
tan-1
(- 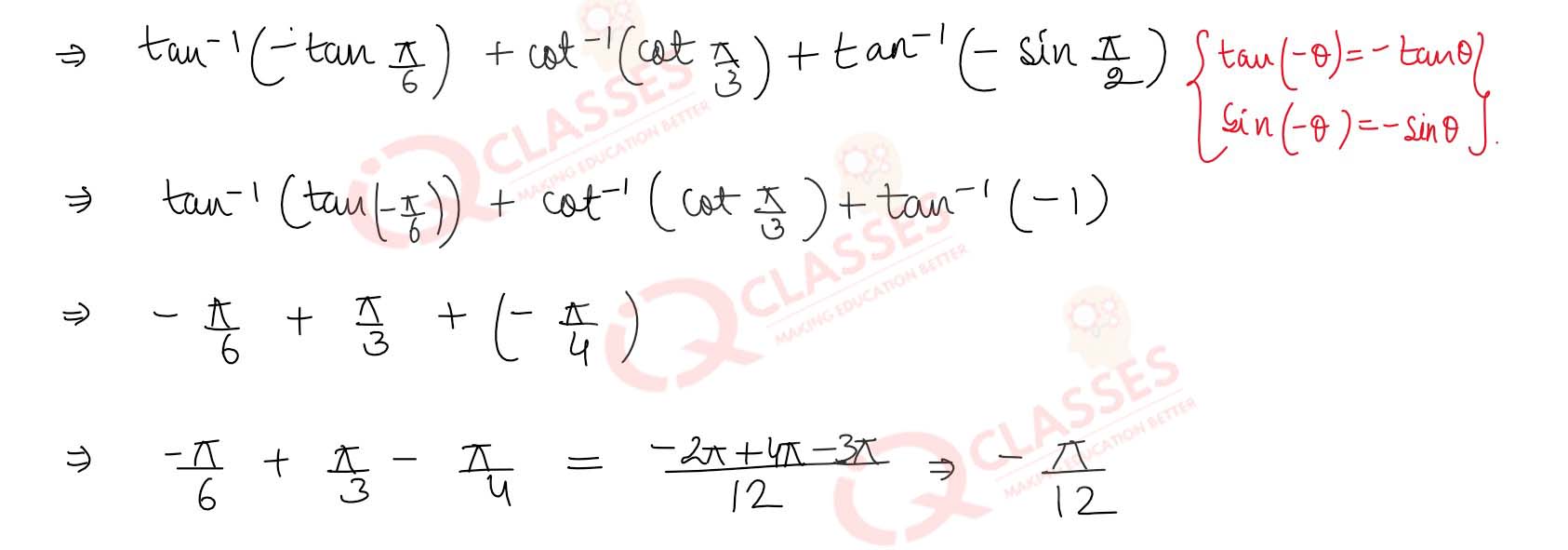
1
/
√3
) + cot-1
(-
1
/
√3
) + tan-1
(sin ( -
π
/
2
))
Solution
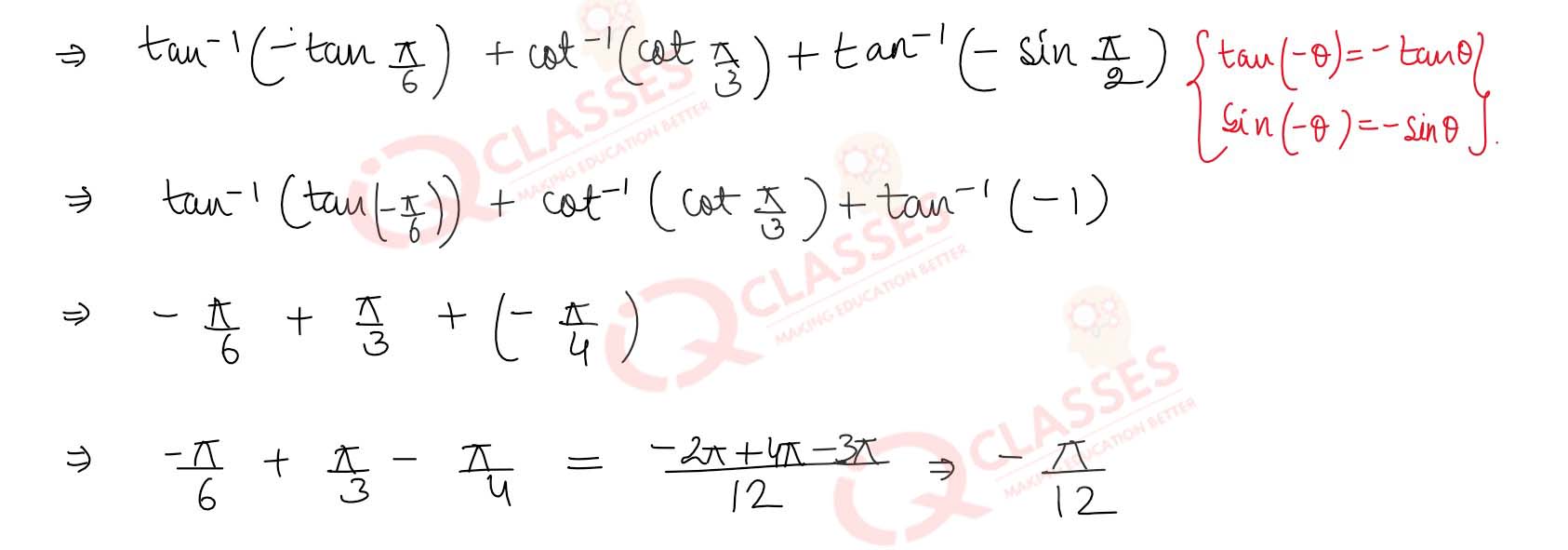
Q16
Write the following in the simplest form :
cot-1 (√1 + x2 - x) Solution

cot-1 (√1 + x2 - x) Solution


Q17
Write the following in the simplest form :
tan-1 (
tan-1 (
3 a2x - x3
/
a3 - 3ax2
)
Solution

Q18
Find the value of :
tan-1 (
tan-1 (
x
/
y
) - tan-1
(
x-y
/
x + y
)
Solution

Q19
cos-1
( 
3
/
5
cosx +
4
/
5
sinx)
Solution

Q20
Prove that :
cos (tan-1 ( sin (cot-1))) = √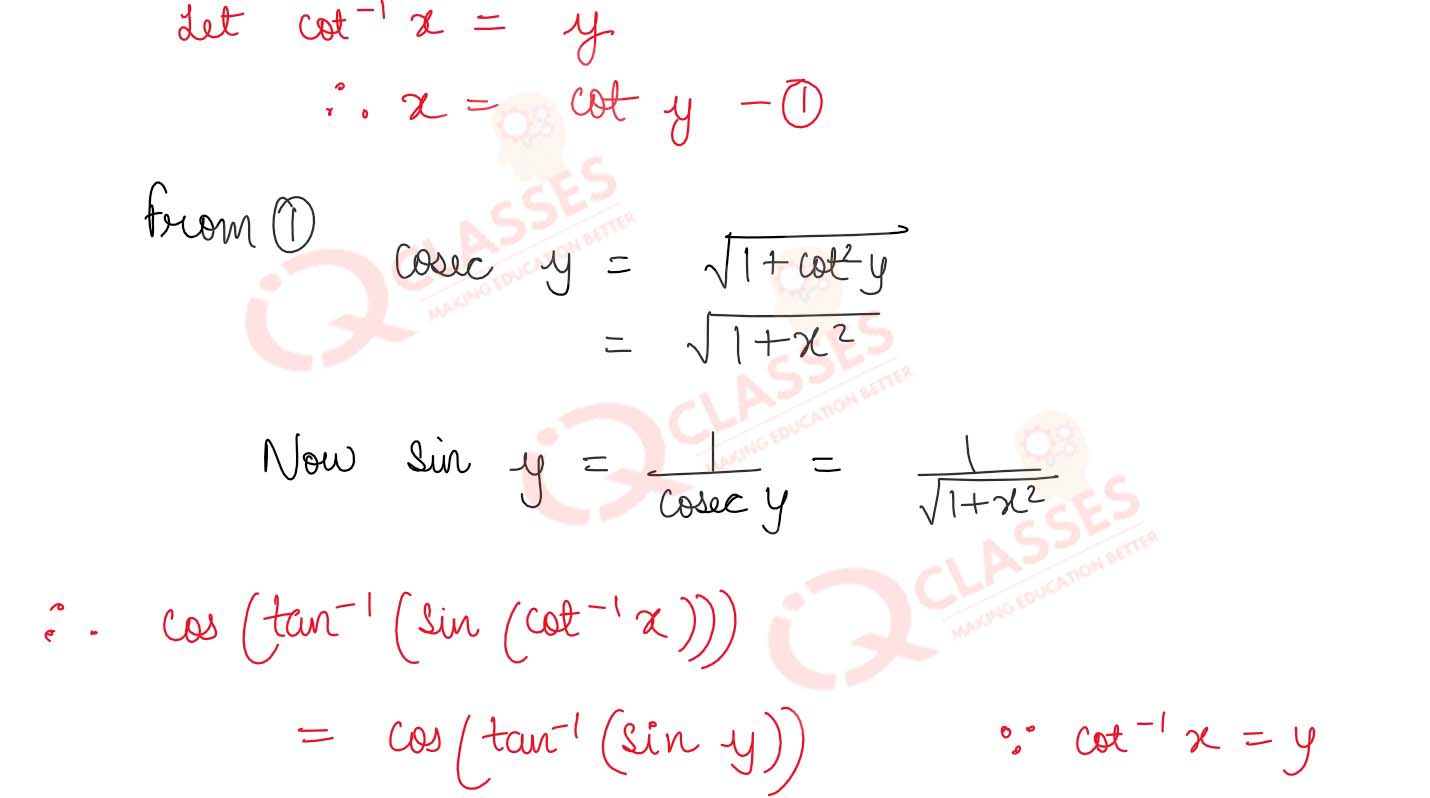

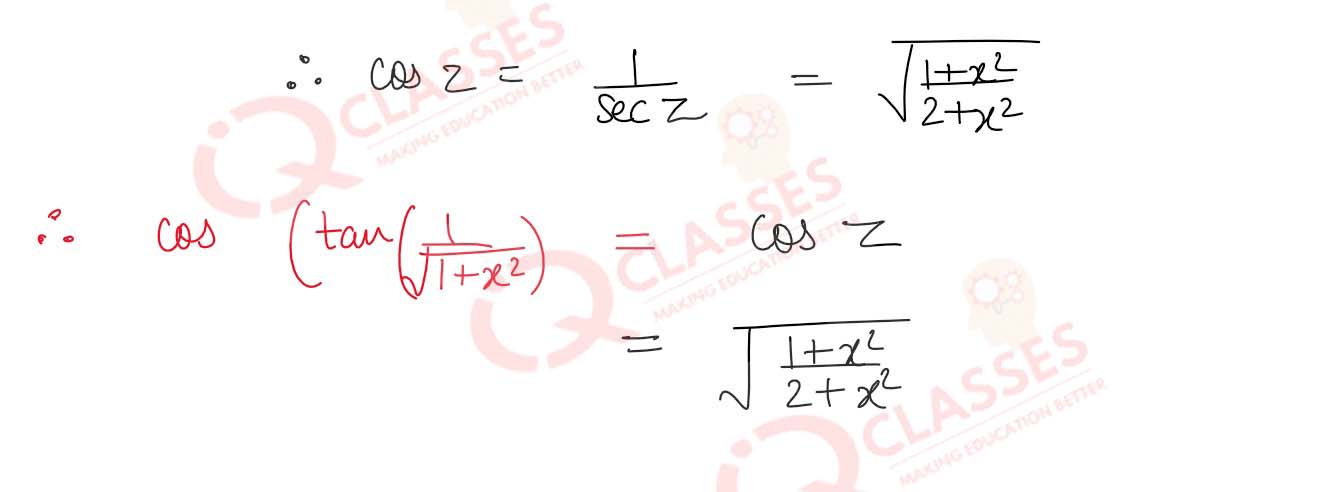
cos (tan-1 ( sin (cot-1))) = √
1 + x2
/
2 + x2
Solution
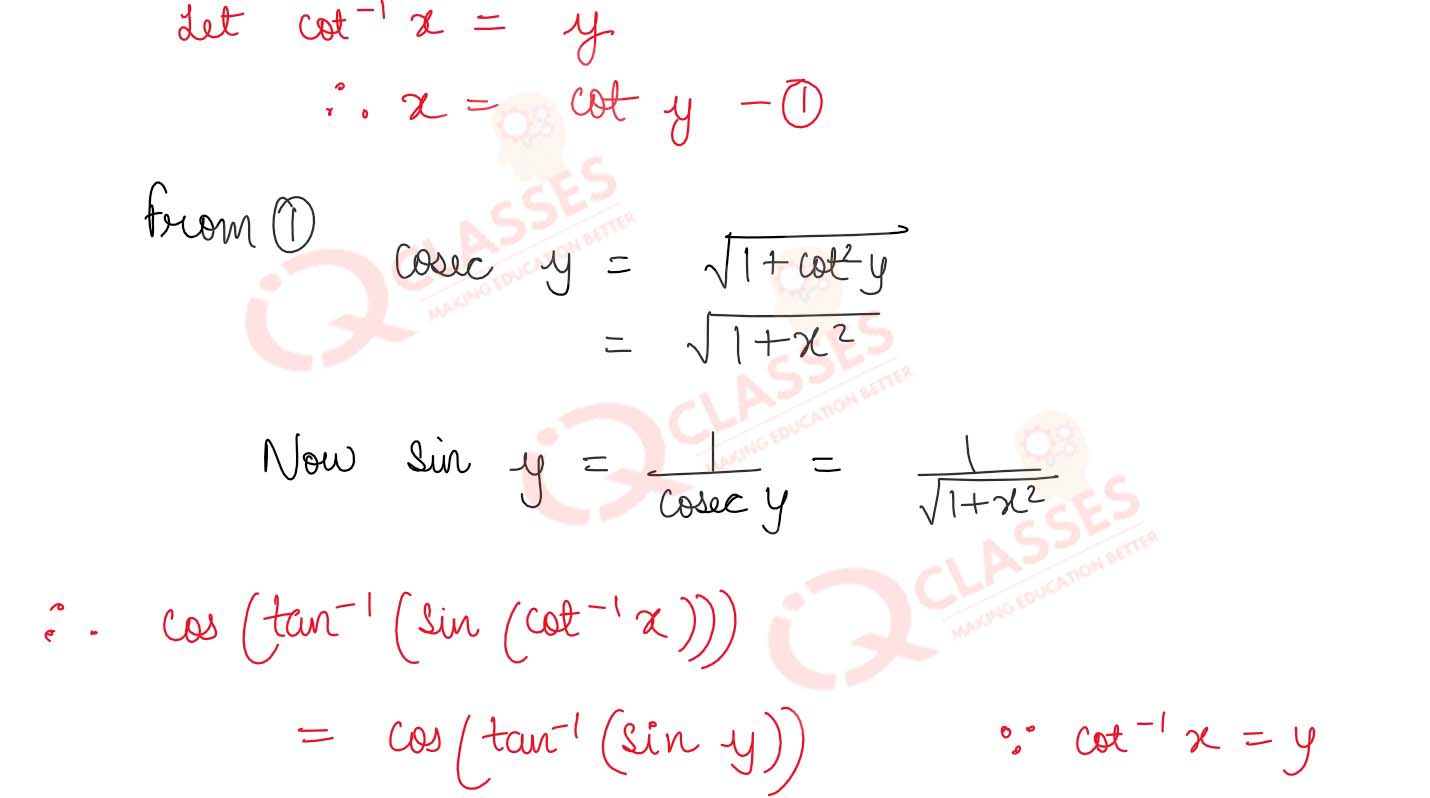

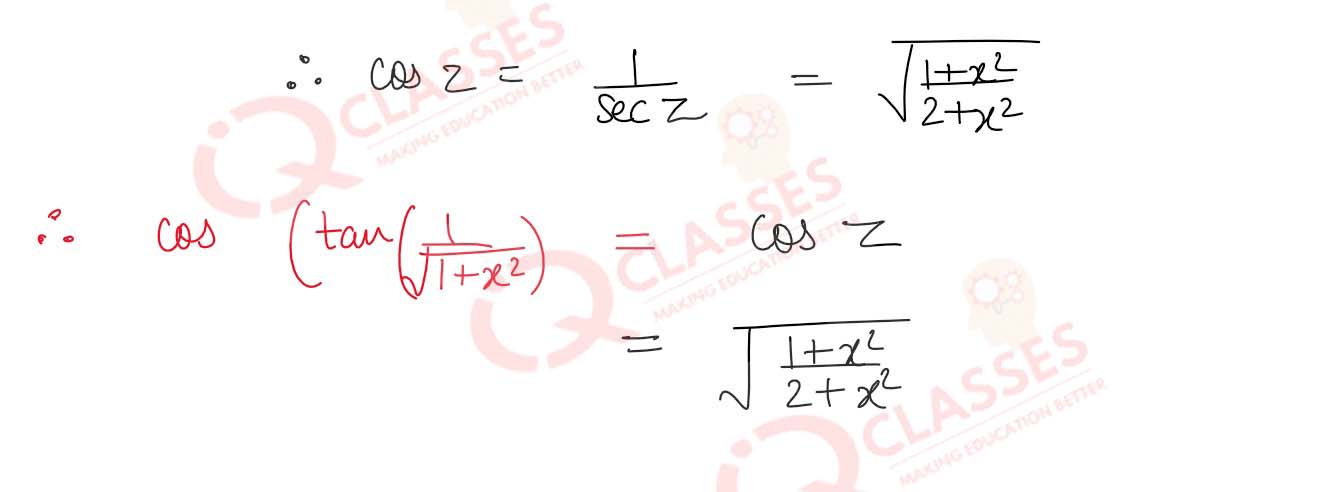
Q21
Prove that cot-1 7 + cot-1 8 + cot-1 18 = cot-1 3
Solution




Q22
Prove that tan-1 1 + tan-1 2 + tan-1 3 = π
Solution
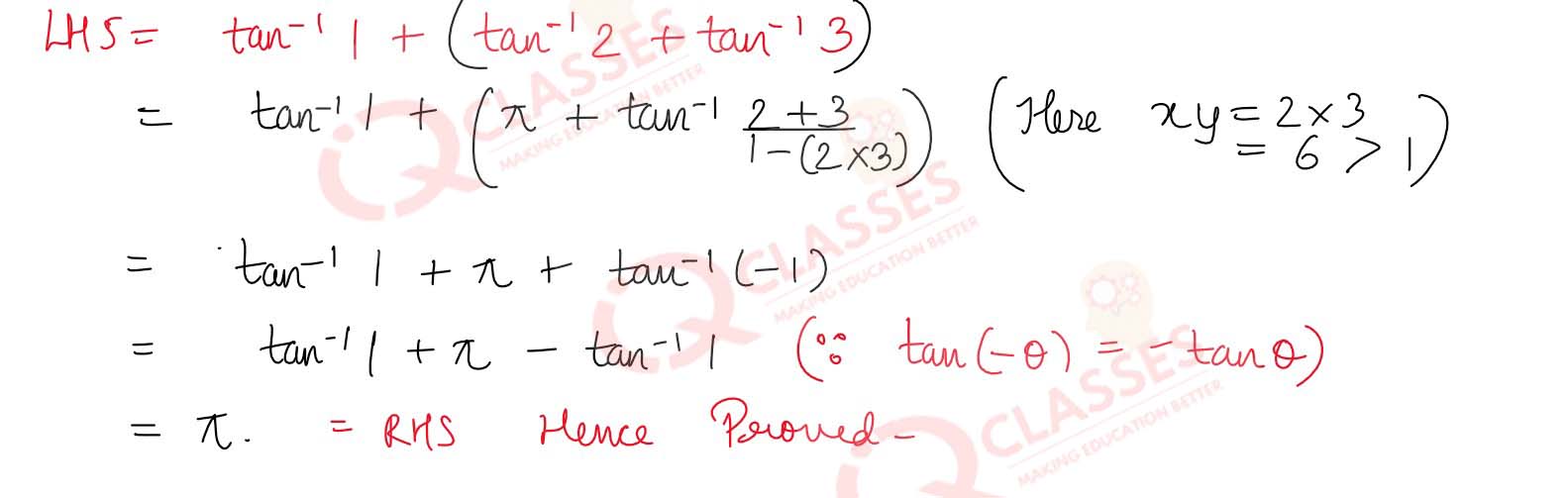
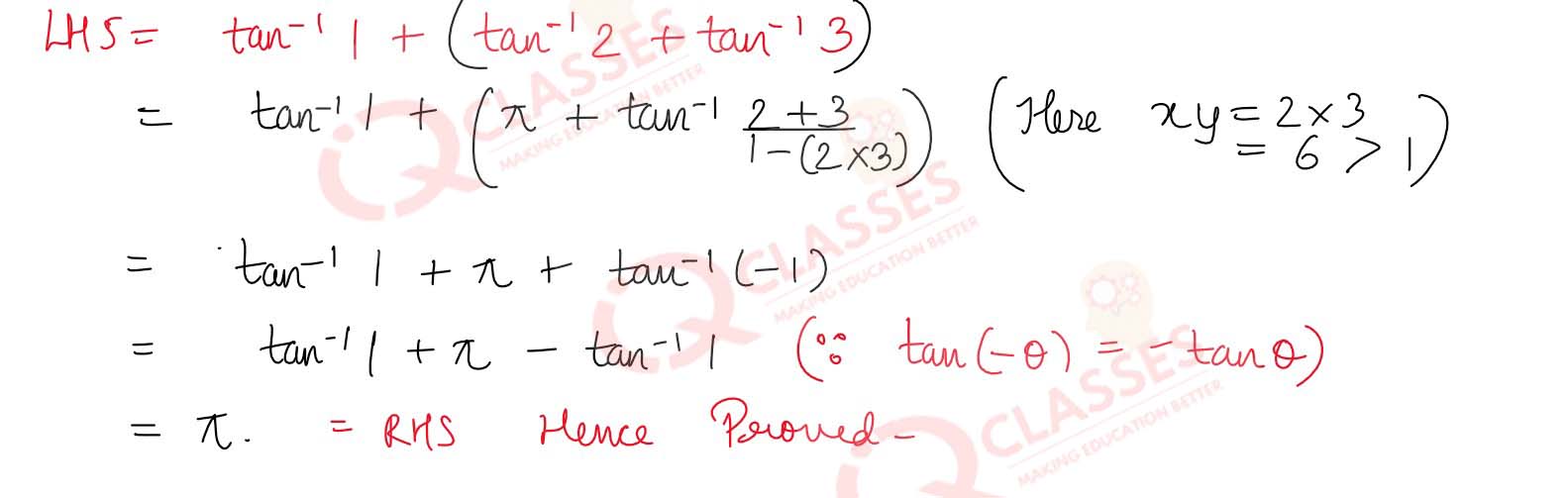
Q23
Prove that : 4(cot-1 3 + cosec-1 √) = π
Solution

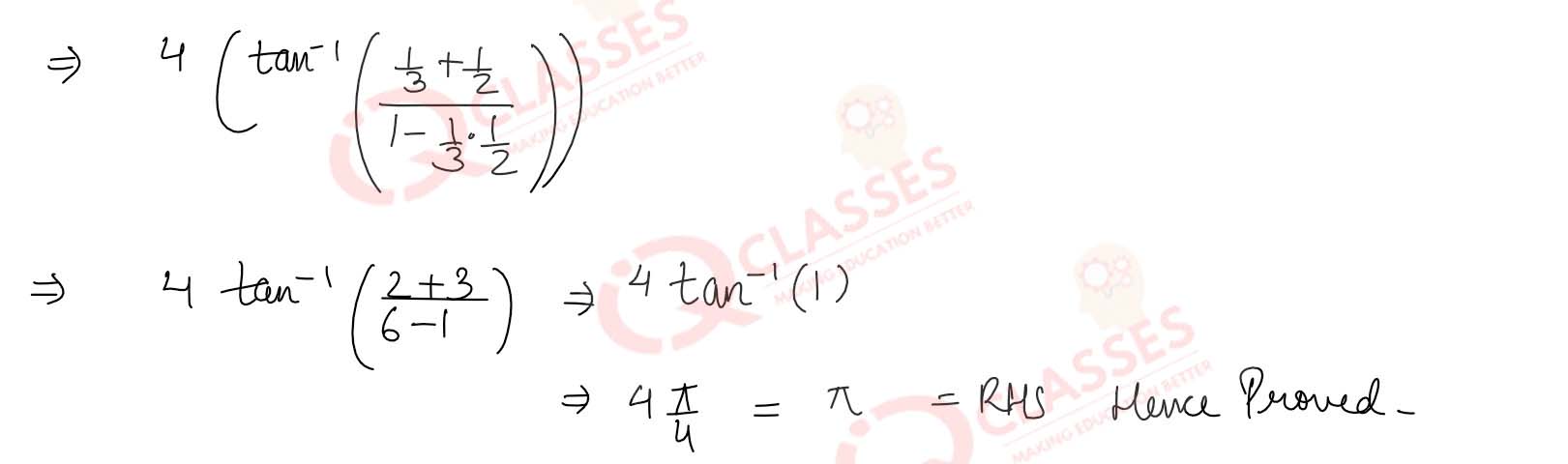

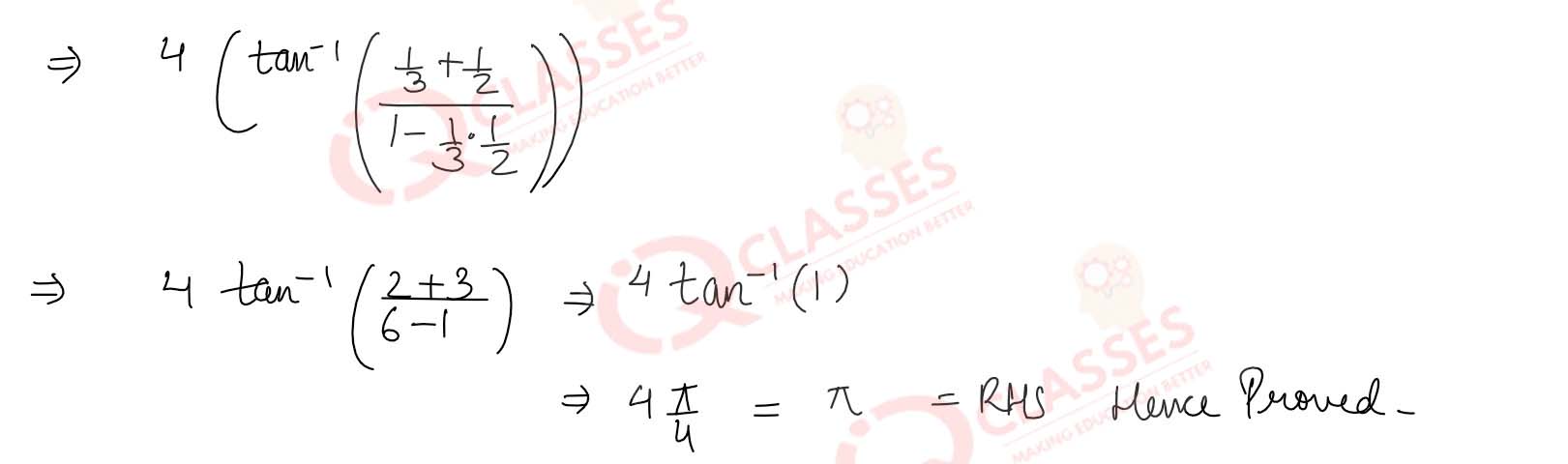
Q24
Prove the following :
tan-1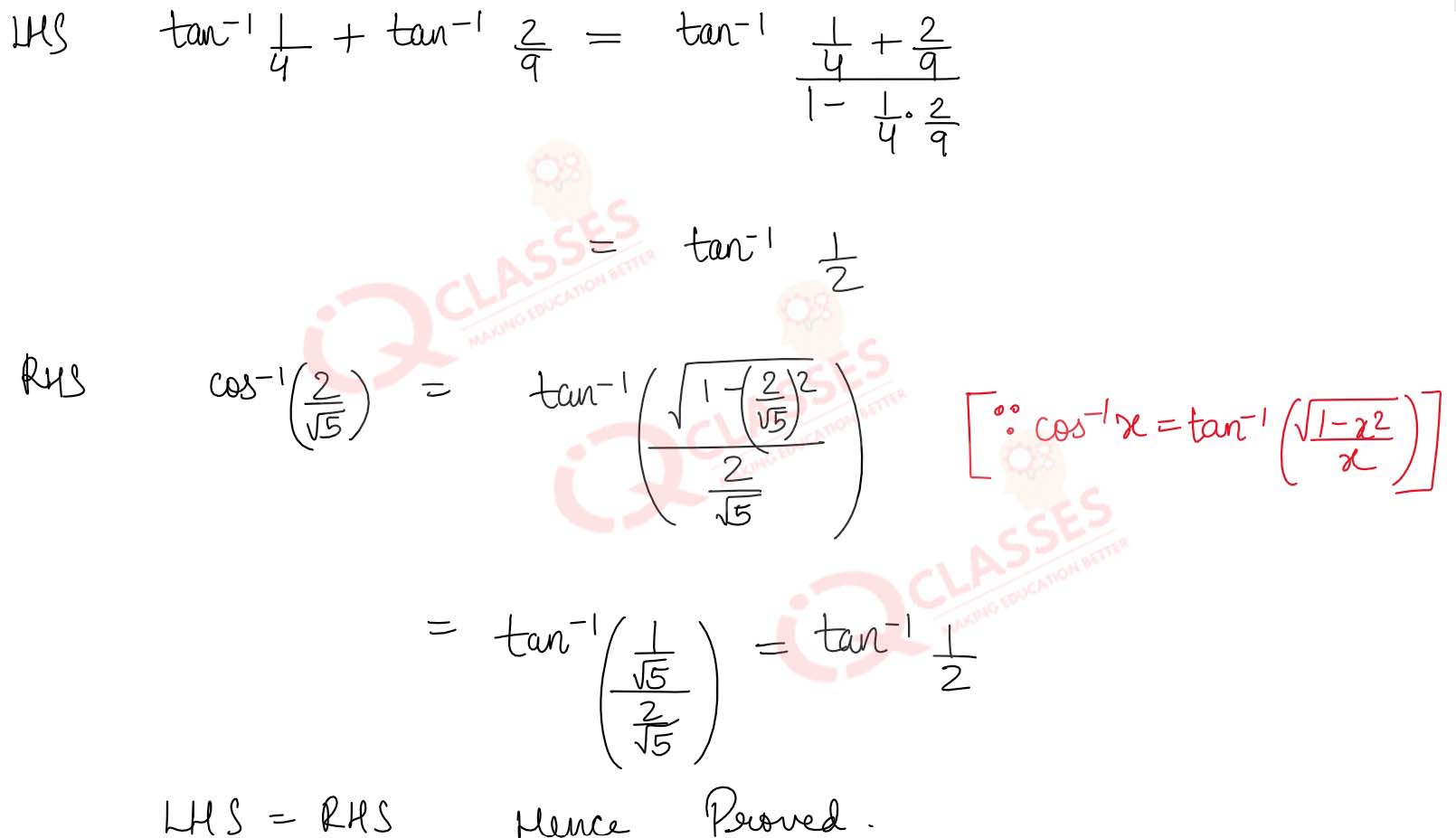
tan-1
1
/
4
+ tan-1
2
/
9
= cos-1
2
/
√5
Solution

Q25
Prove the following :
tan-1
tan-1
1
/
4
+ tan-1
2
/
9
=
1
/
2
sin-1
4
/
5
Solution

Q26
If sin-1x + sin-1 y + sin-1 z = π then prove that :
(i) x2 - y2 - z2 + 2yz √ 1 - x2 = 0
(ii) x4 + y4 + z4 + 4x2 y2 z2 = 2 (x2 y2 + y2 z2 + z2 x2) Solution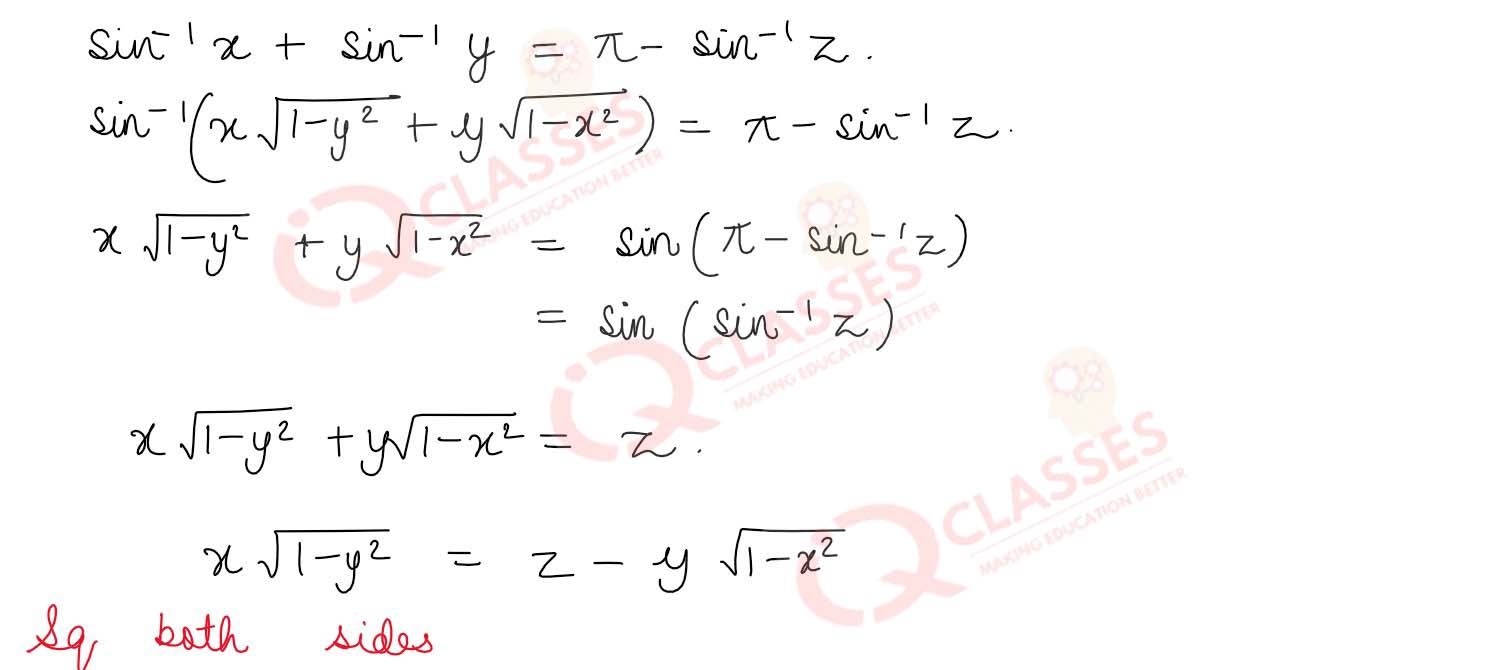


(i) x2 - y2 - z2 + 2yz √ 1 - x2 = 0
(ii) x4 + y4 + z4 + 4x2 y2 z2 = 2 (x2 y2 + y2 z2 + z2 x2) Solution
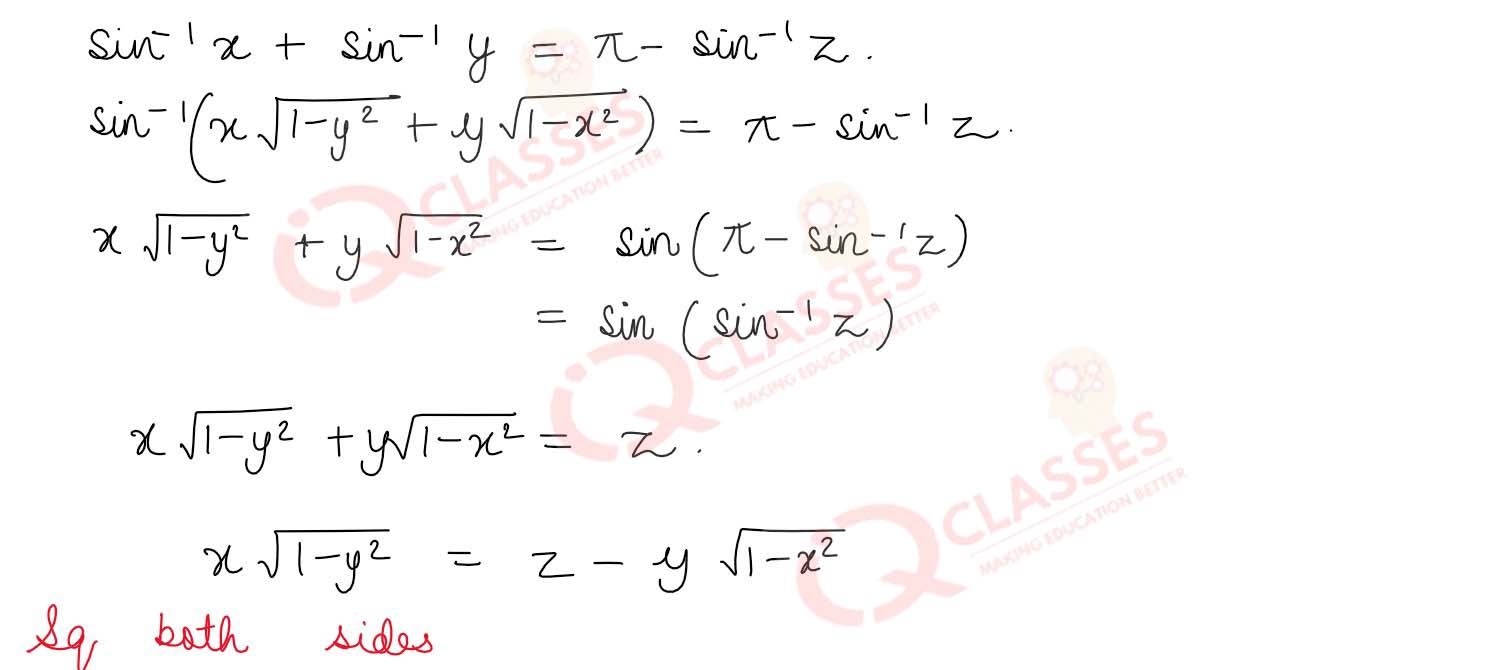


Q27
Evaluate :
sin-1
( sin(10))
Solution


Q28
Evaluate :
tan-1
(tan(-6))
Solution


Q29
cos-1
(cos(- 
5π
/
6
)) ≠
- π
/
6
, What is its value
Solution



Add a comment