Class 12 Maths ISC Application of Calculus Board Questions
Here we provide Class 12 Maths important notes,board questions and predicted questions with Answers for chapter Application of Calculus. These important notes,board questions and predicted questions are based on ISC board curriculum and correspond to the most recent Class 12 Maths syllabus. By practising these Class 12 materials, students will be able to quickly review all of the ideas covered in the chapter and prepare for the Class 12 Board examinations.
class 12 ISC Application of Calculus BoardQuestions
Application of Calculus BoardQuestions
2016
Q1
(a) The demand function is x=24-2p /3 where x is the number of units demanded and p is the price per
unit.
Find:
(i) The revenue function R in terms of p.
(ii) The price and the number of units demanded which the revenue is maximum
solutions
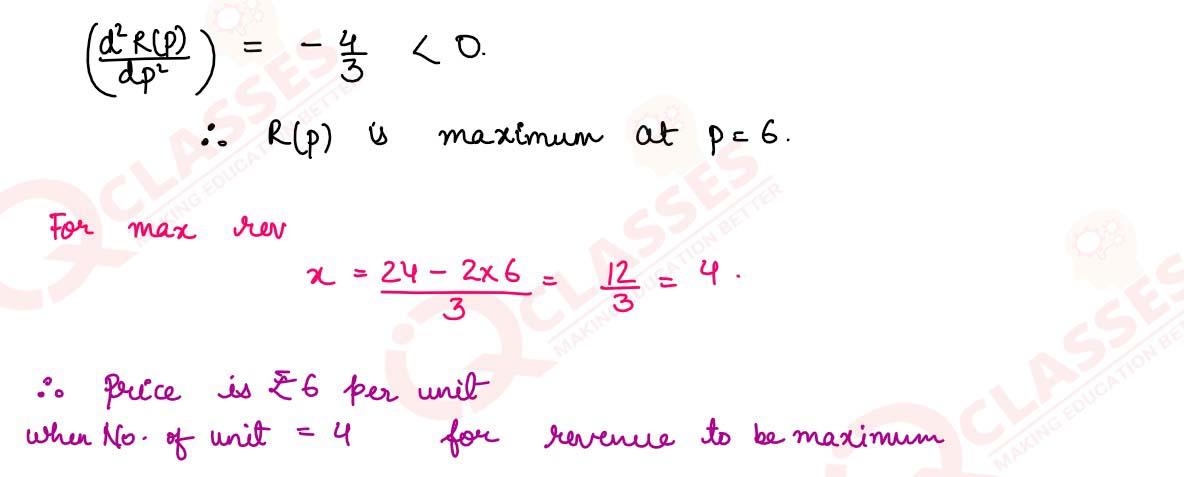
Find:
(i) The revenue function R in terms of p.
(ii) The price and the number of units demanded which the revenue is maximum
solutions

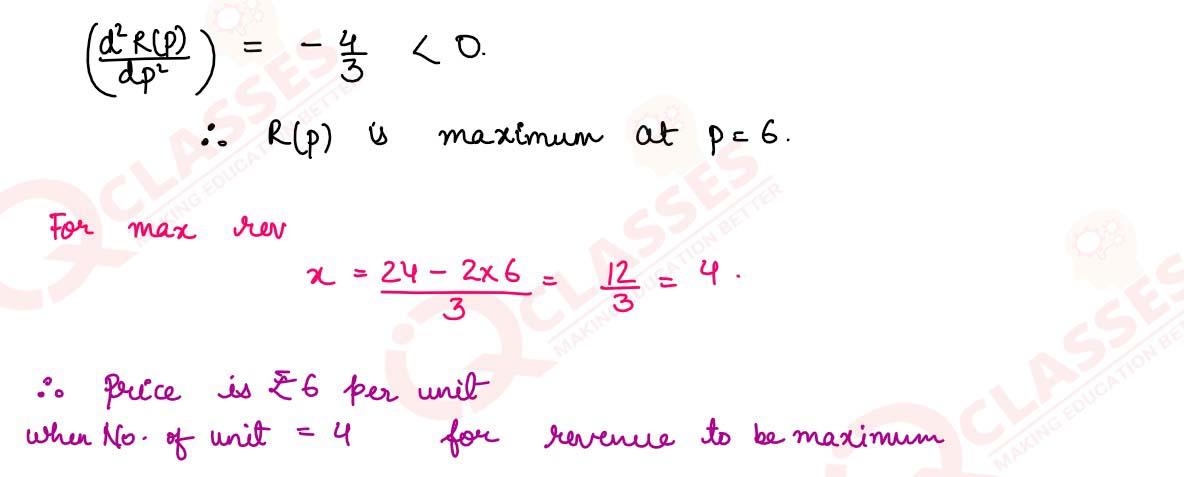
2017
Q1
(a) The demand for a certain product is represented by the equation p= 500 + 25x -x3/3 in
rupees,
where x is the number of units and p is the price per unit. Find:
(i) Marginal revenue function.
(ii) The marginal revenue when 10 units are sold.
solutions
(i) Marginal revenue function.
(ii) The marginal revenue when 10 units are sold.
solutions

2018
Q1
(a) Given the total cost function for x units of a commodity as:
C(x)=1/3 x3 + 3x2 16x+2
Find:
(i) Marginal cost function
(ii) Average cost function
(c) The average cost function associated with producing and marketing x units of an tem is given by AC=2x-11 + 50/x . Find the range of values of the outputx, for which AC is increasing.
solutions

C(x)=1/3 x3 + 3x2 16x+2
Find:
(i) Marginal cost function
(ii) Average cost function
(c) The average cost function associated with producing and marketing x units of an tem is given by AC=2x-11 + 50/x . Find the range of values of the outputx, for which AC is increasing.
solutions


Q2
(a) A product can be manufactured at a total cost C(x) = x2/100 + 100x + 40
, where x is the number of
units produced. The price at which each unit can be sold is given by P =(200 - x/400)
Determine the production level x at which the profit is maximum. What are the price per unit and total profit at the level of production?
Or
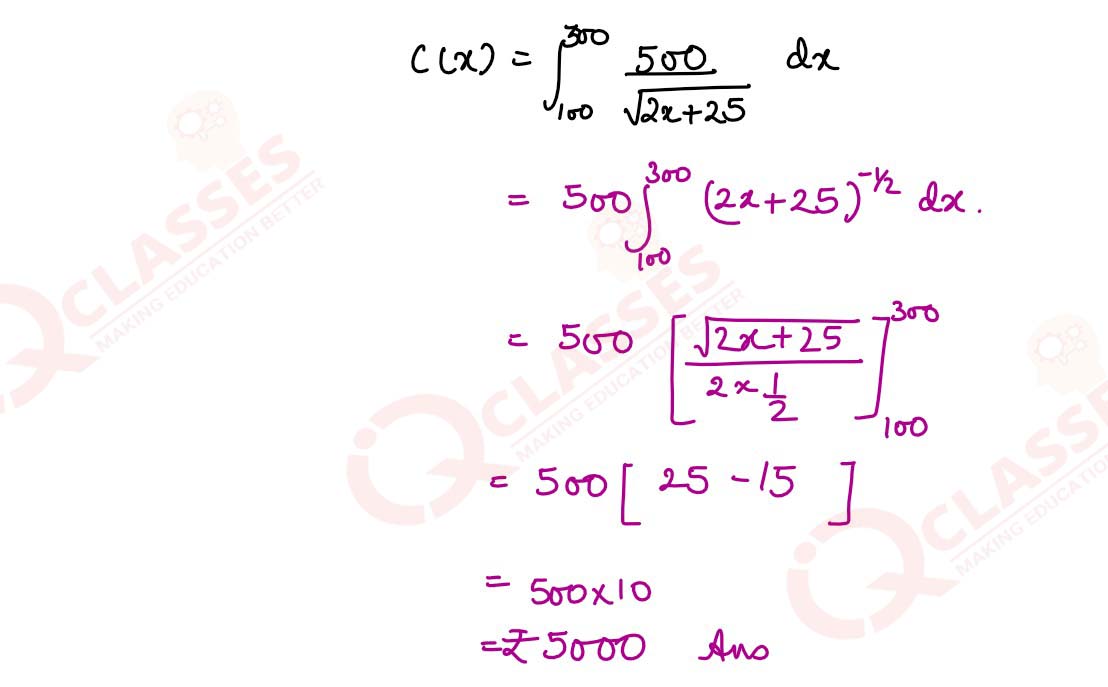
(b) A manufacturers marginal cost function is 500/√2x+25 Find the cost involved to increase production from 100 units to 300 units.
solutions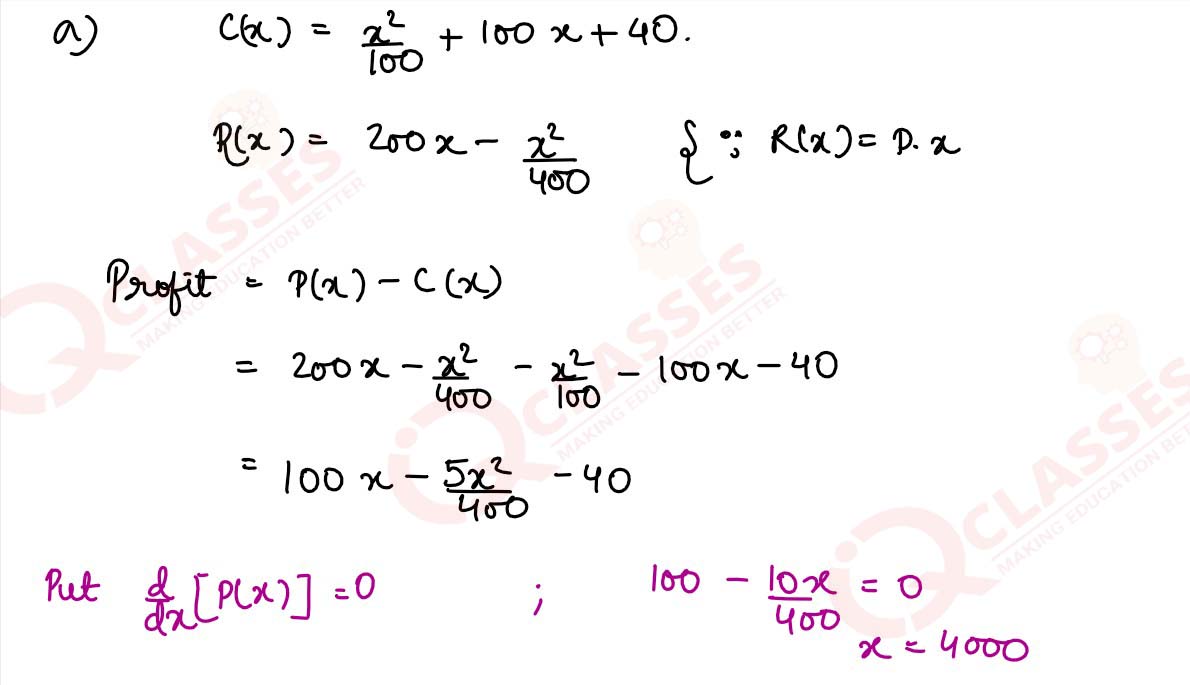
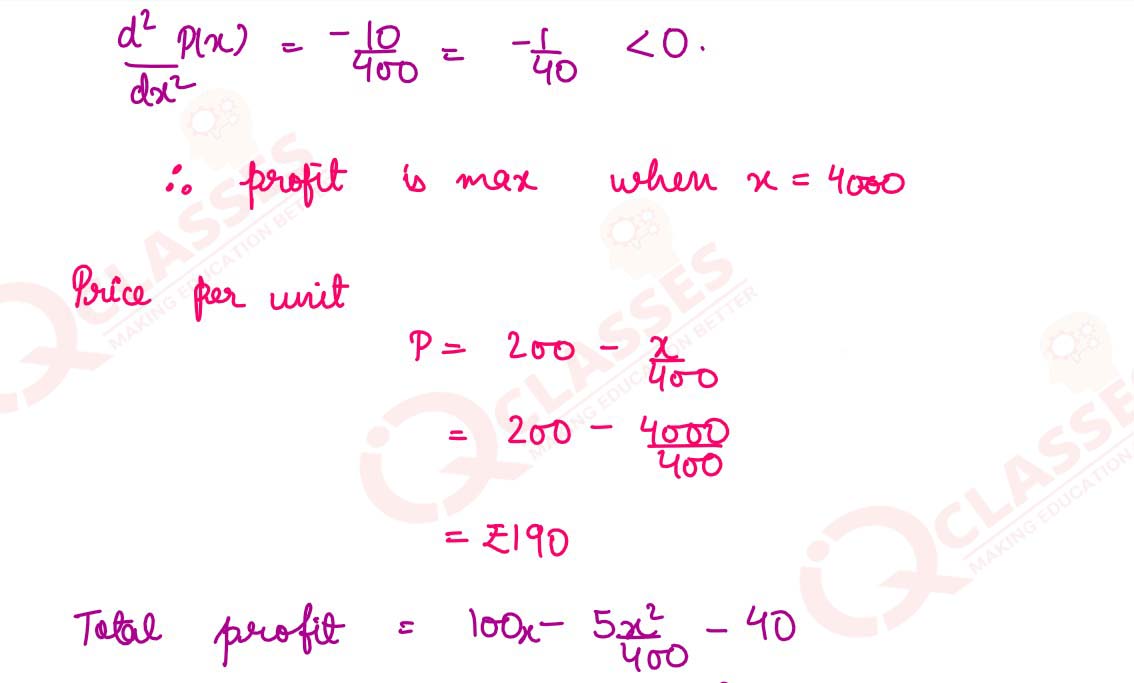

Determine the production level x at which the profit is maximum. What are the price per unit and total profit at the level of production?
Or
(b) A manufacturers marginal cost function is 500/√2x+25 Find the cost involved to increase production from 100 units to 300 units.
solutions
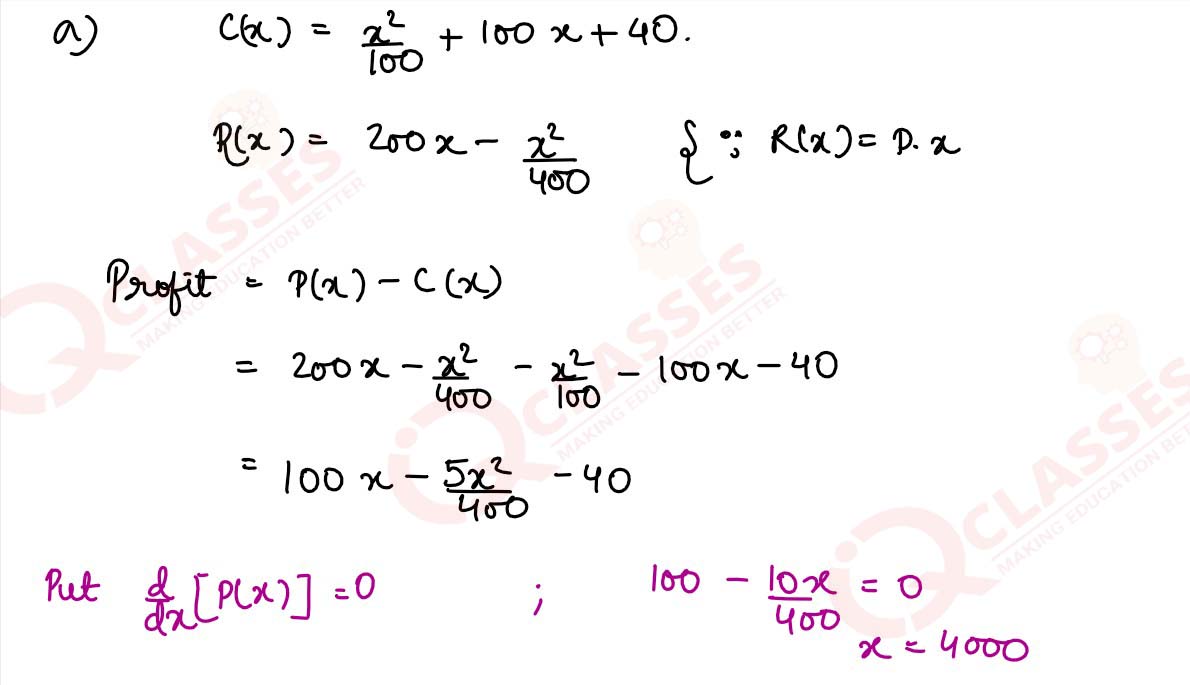
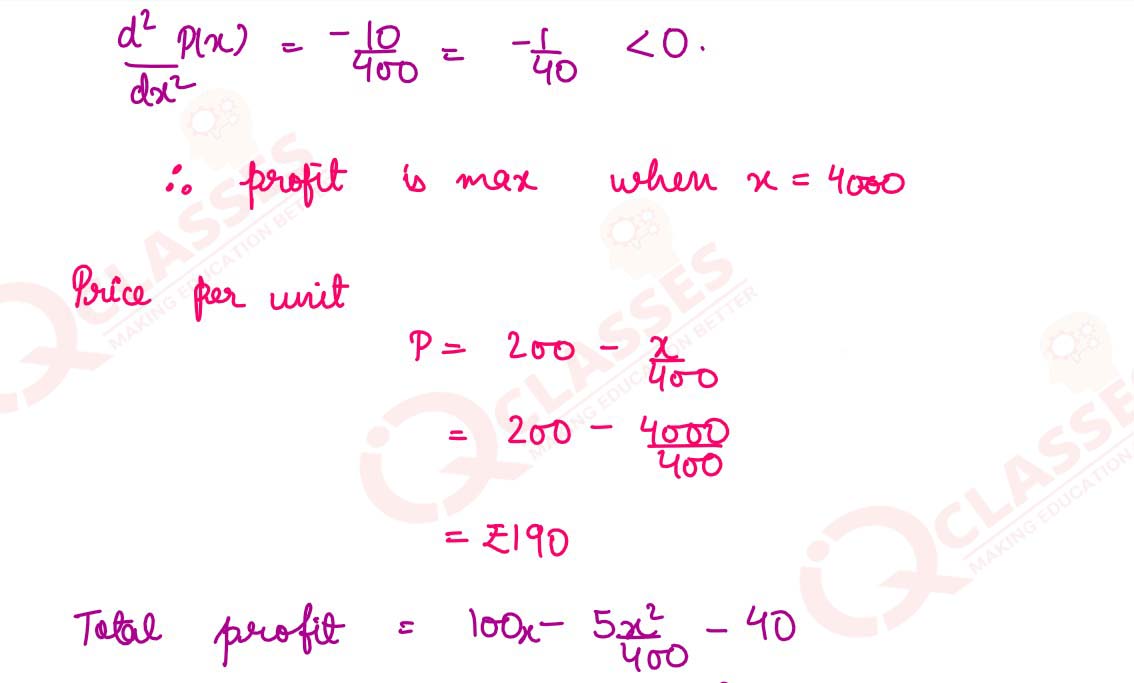


2019
Q1
(a) A product can be manufactured at a total cost C(x) = x2/100 + 100x + 40
, where x is the number of
units produced. The price at which each unit can be sold is given by P =(200 - x/400)
Determine the production level x at which the profit is maximum. What are the price per unit and total profit at the level of production?
Or
(b) A manufacturers marginal cost function is 500/√2x+25. Find the cost involved to increase production from 100 units to 300 units.
solutions


Determine the production level x at which the profit is maximum. What are the price per unit and total profit at the level of production?
Or
(b) A manufacturers marginal cost function is 500/√2x+25. Find the cost involved to increase production from 100 units to 300 units.
solutions



2020
Q1
(a) The selling price of a commodity is fixed at ₹60 and its cost function is
C(x) -35 x +250
(i) Determine the profit function.
(ii) Find the break even points.
(b) The revenue function is given by R(x)=100x-x2-x3. Find
(i) The demand function.
(ii) Marginal revenue function.
(c) For the lines Of regression 4x — 2y = 4 and 2x-3y +6=0 find the mean of 'x' and the mean of 'y'
solutions

C(x) -35 x +250
(i) Determine the profit function.
(ii) Find the break even points.
(b) The revenue function is given by R(x)=100x-x2-x3. Find
(i) The demand function.
(ii) Marginal revenue function.
(c) For the lines Of regression 4x — 2y = 4 and 2x-3y +6=0 find the mean of 'x' and the mean of 'y'
solutions


Q2
(a)
The marginal cost of the production of the commodity is 30 + 2x, it is known that
fixed costs are ₹200, find
(i) The total cost
(ii) The cost of increasing output from 100 to 200 units.
OR
The total cost function ofa firm is given by C(x)=1/3 x3 — 5x2 + 30 x— 15 where the selling price per unit is given as ₹6 . Find for what value Of x will the profit be max 'mum.
solutions

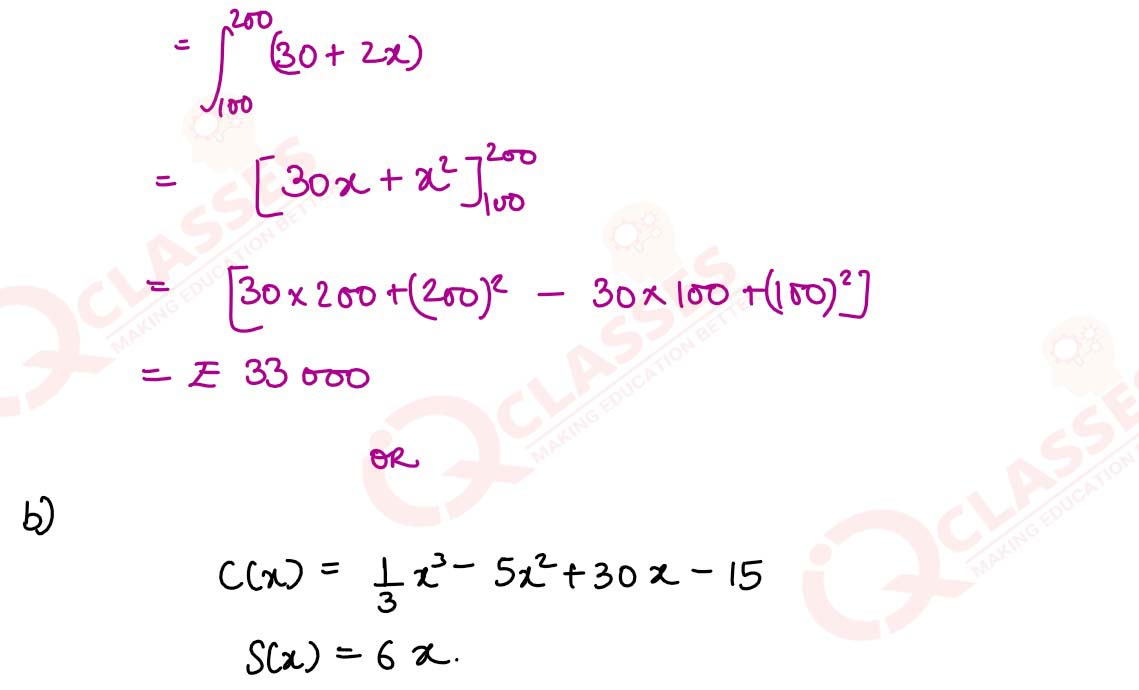
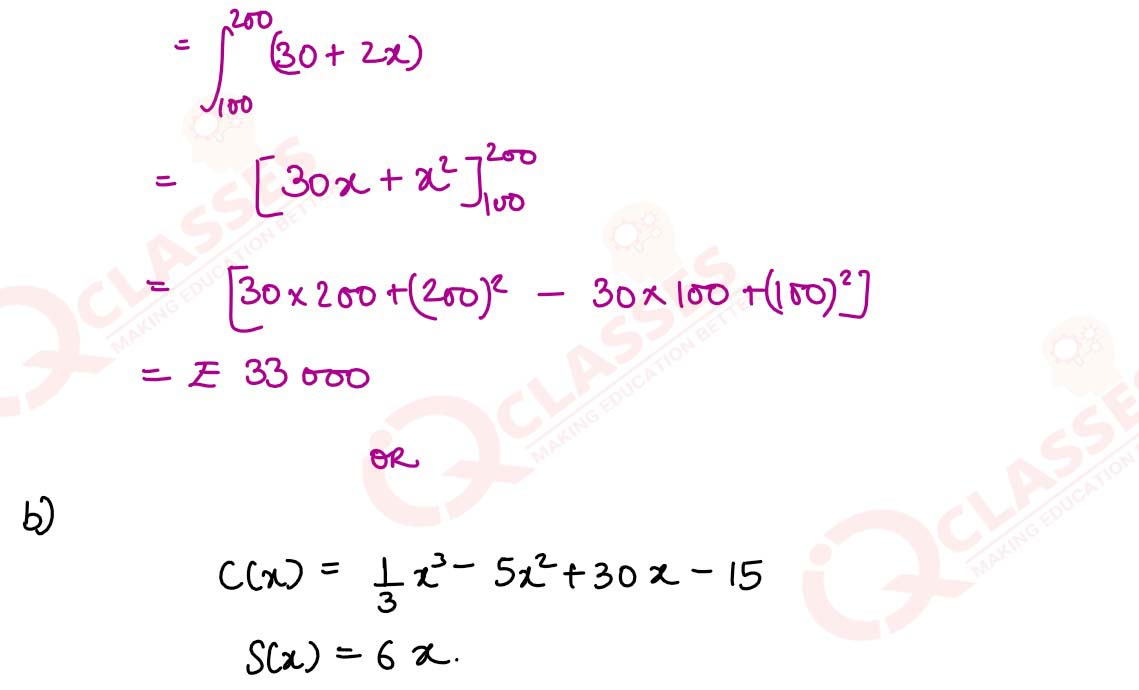

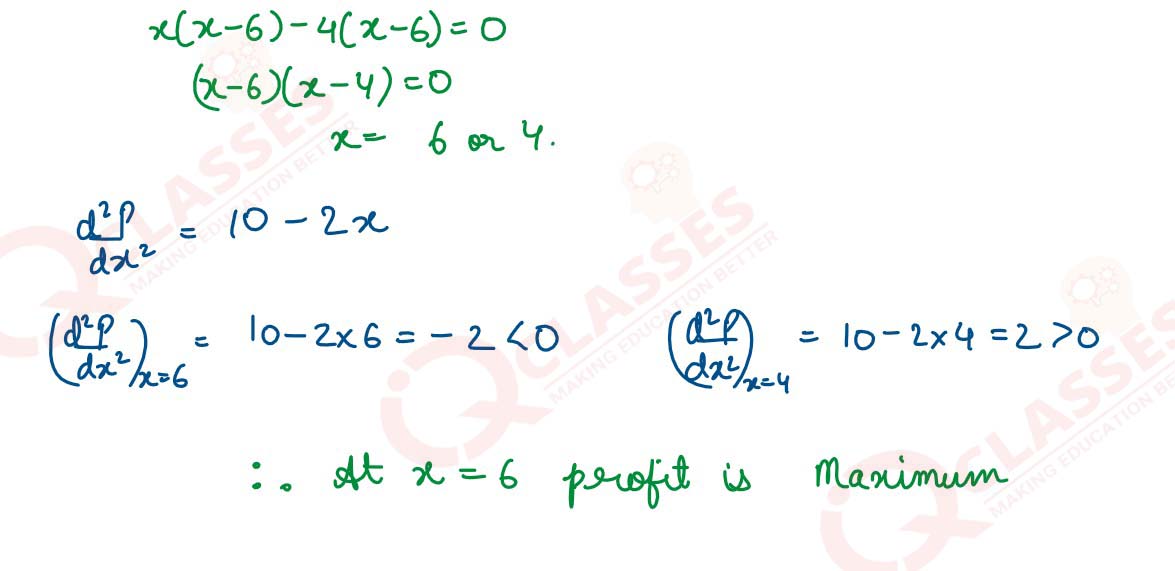
(i) The total cost
(ii) The cost of increasing output from 100 to 200 units.
OR
The total cost function ofa firm is given by C(x)=1/3 x3 — 5x2 + 30 x— 15 where the selling price per unit is given as ₹6 . Find for what value Of x will the profit be max 'mum.
solutions


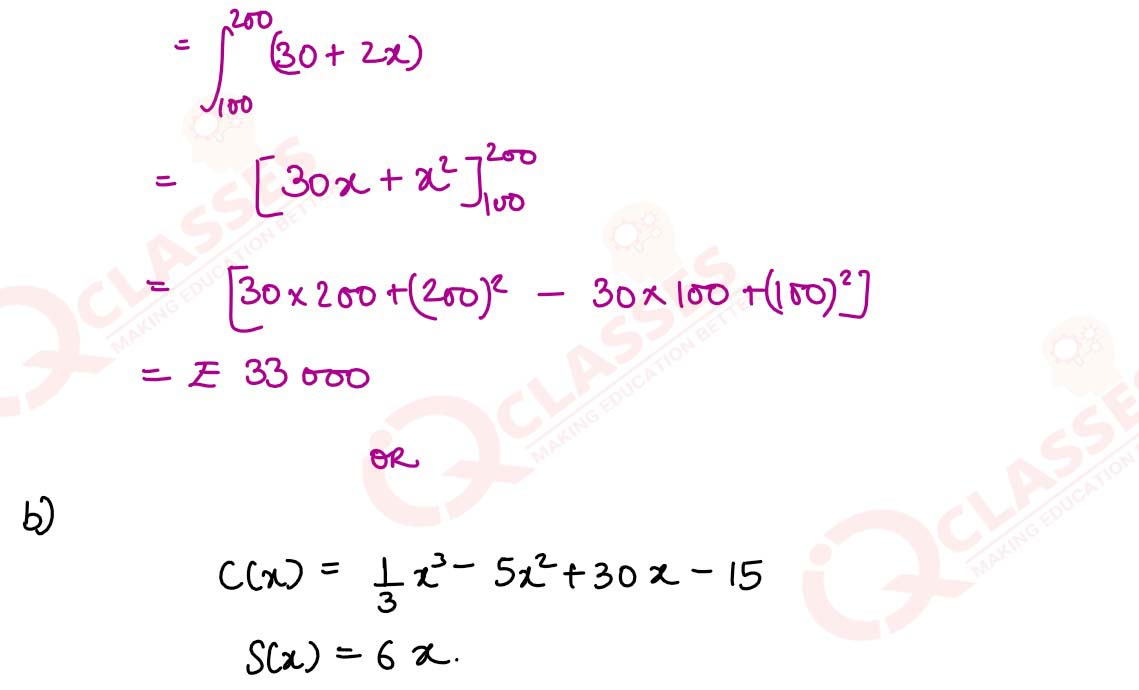
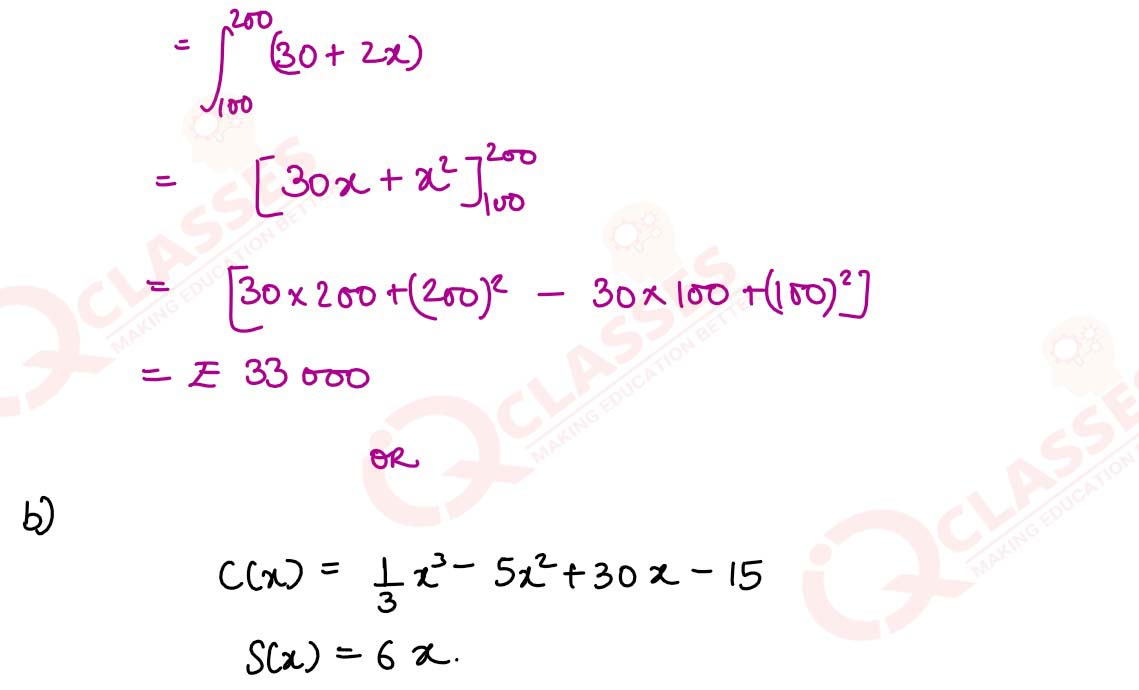

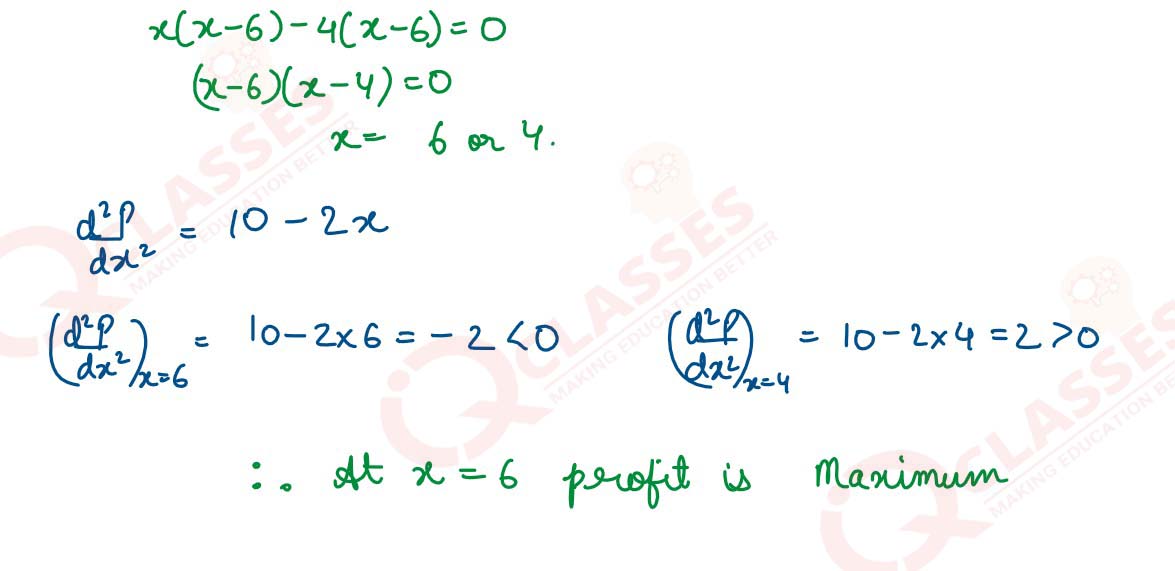

Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment