Class 12 ISC Maths Continuity & Differentiability Board Questions
Continuity and differentiability in class 12 is about, if a function f(x) is said to be continuous at a point x = a, if Left hand limit of f(x) at(x = a) = Right hand limit of f(x) at (x = a) = Value of f(x) at (x = a) i.e. if at x = a, LHL = RHL = f(a)
2016
Q1
Verify the conditions of Rolle's Theorem for the following function:
f(x)=log(x2+ 2) — log 3 on [-1, 1]
Find a point in the interval, where the tangent to the curve is parallel to x-axis.
solutions

f(x)=log(x2+ 2) — log 3 on [-1, 1]
Find a point in the interval, where the tangent to the curve is parallel to x-axis.
solutions


Q1
Verify the conditions of Rolle's Theorem for the following function:
f(x)=log(x2+ 2) — log 3 on [-1, 1]
Find a point in the interval, where the tangent to the curve is parallel to x-axis.
solutions

f(x)=log(x2+ 2) — log 3 on [-1, 1]
Find a point in the interval, where the tangent to the curve is parallel to x-axis.
solutions


Q2
Using L'Hospital's Rule, evaluate:
limx->0(
solutions

limx->0(
1
/
x2
-
cotx
/
x
)
solutions


2017
Q1
Verify Langrange's mean value theorem for the function:
f(x) = x (l — log x) and find the value of 'c' in the interval [1, 2]
solutions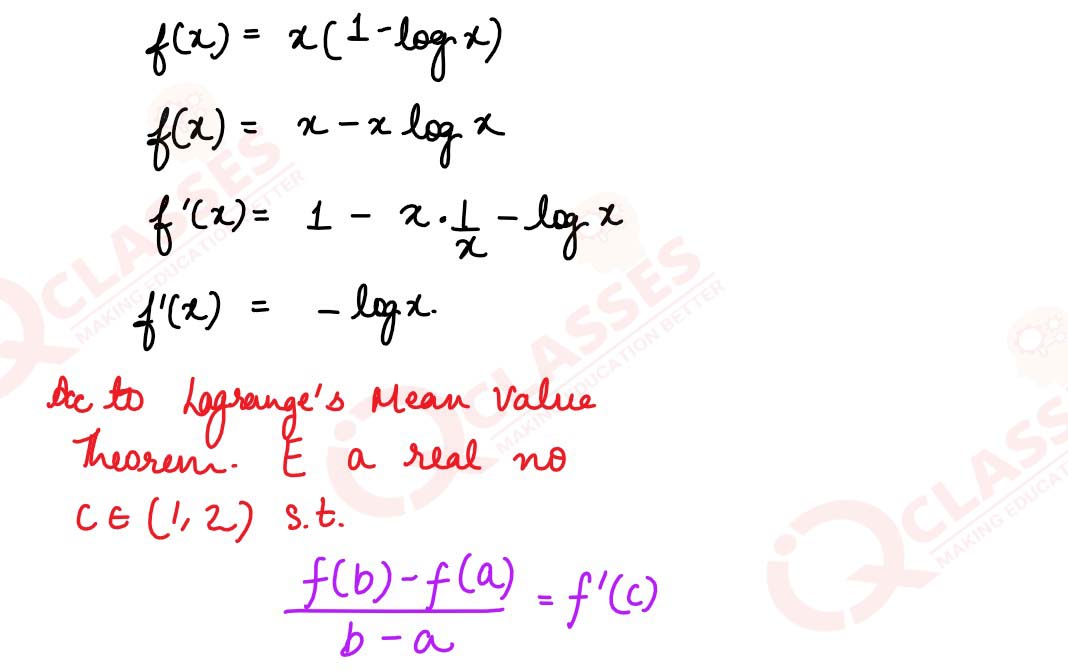
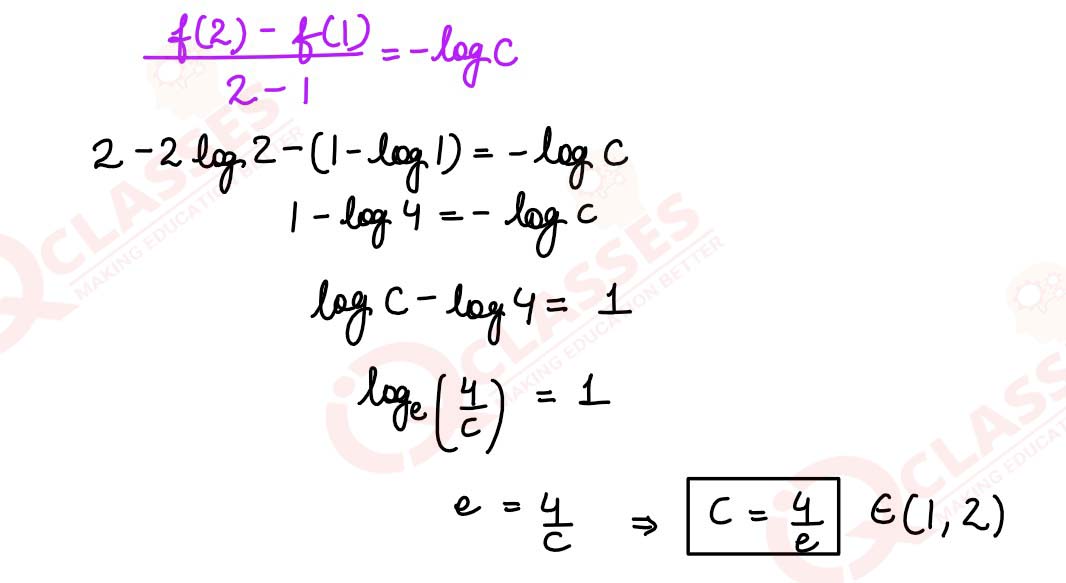
f(x) = x (l — log x) and find the value of 'c' in the interval [1, 2]
solutions
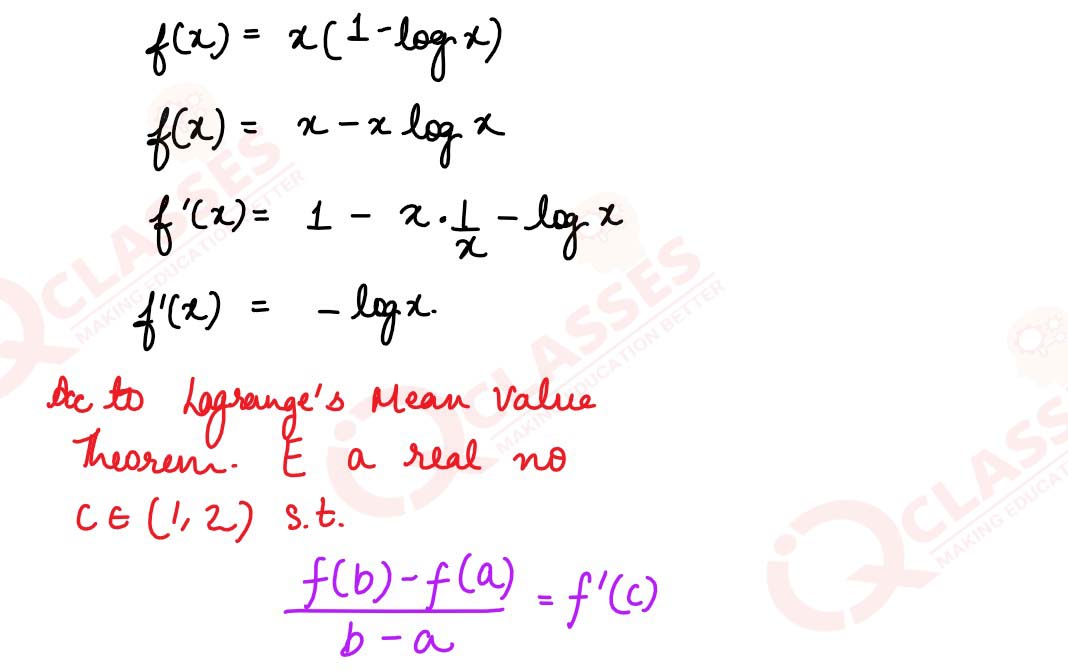
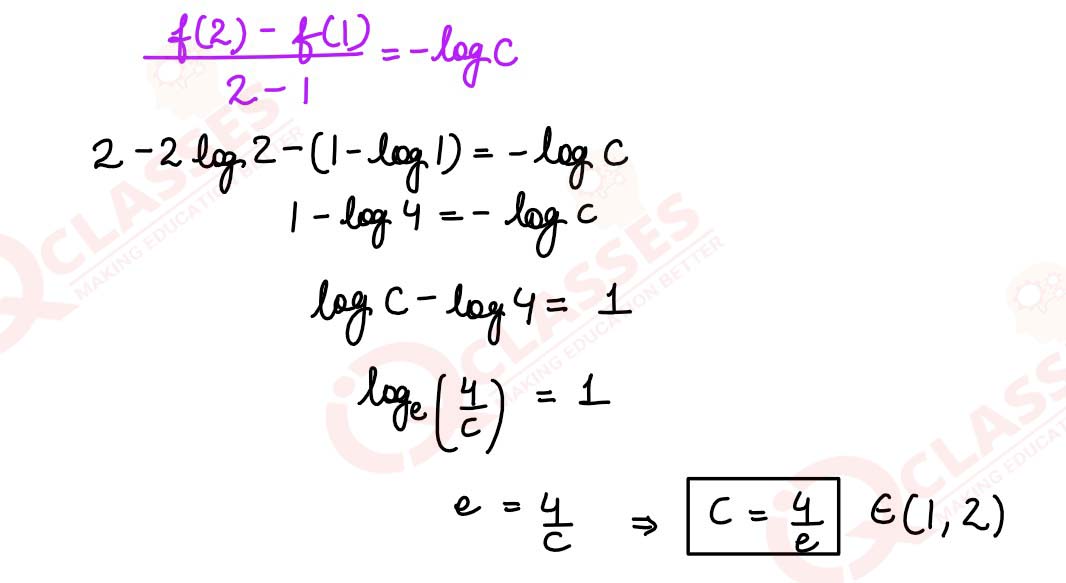
Q2
Using L'Hospital's Rule, evaluate:
It (x --> π/2) (x tanx - π/4 . sec x)
solutions
It (x --> π/2) (x tanx - π/4 . sec x)
solutions

2018
Q1
(a) Show that the function f(x) =
is continuous at x = 1 but not differentiable
OR
(b) Verify Rolle's theorem for the following function: f (x) = e-x sin x on [0, π]
solutions



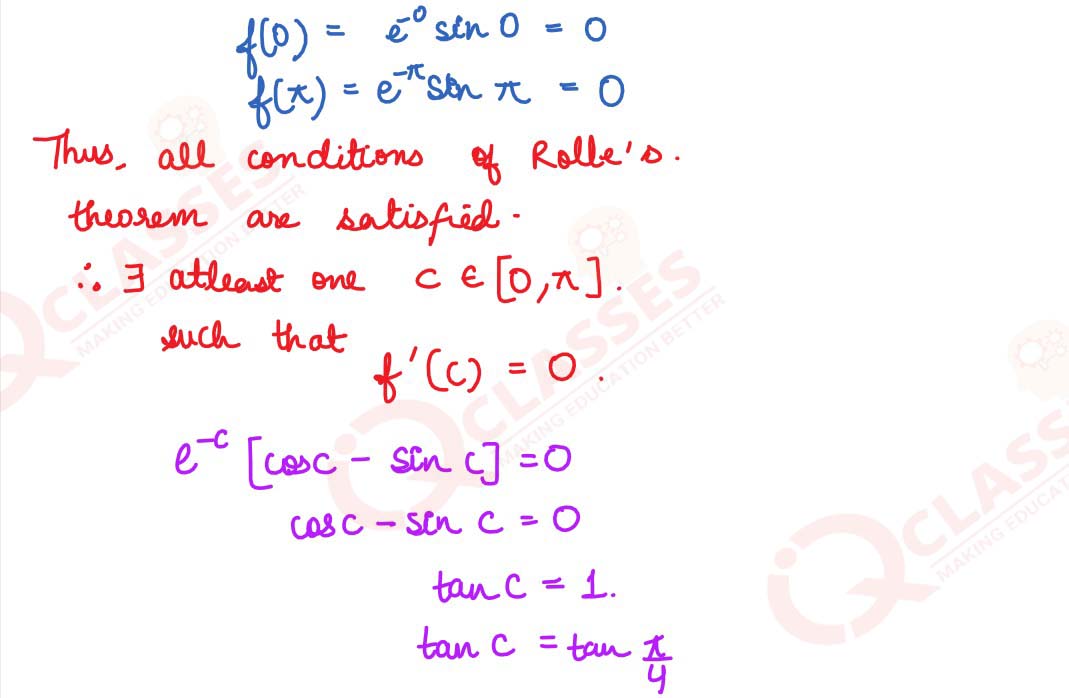

| x2,x≤1 |
|
1
/
x
,x>1
|
OR
(b) Verify Rolle's theorem for the following function: f (x) = e-x sin x on [0, π]
solutions




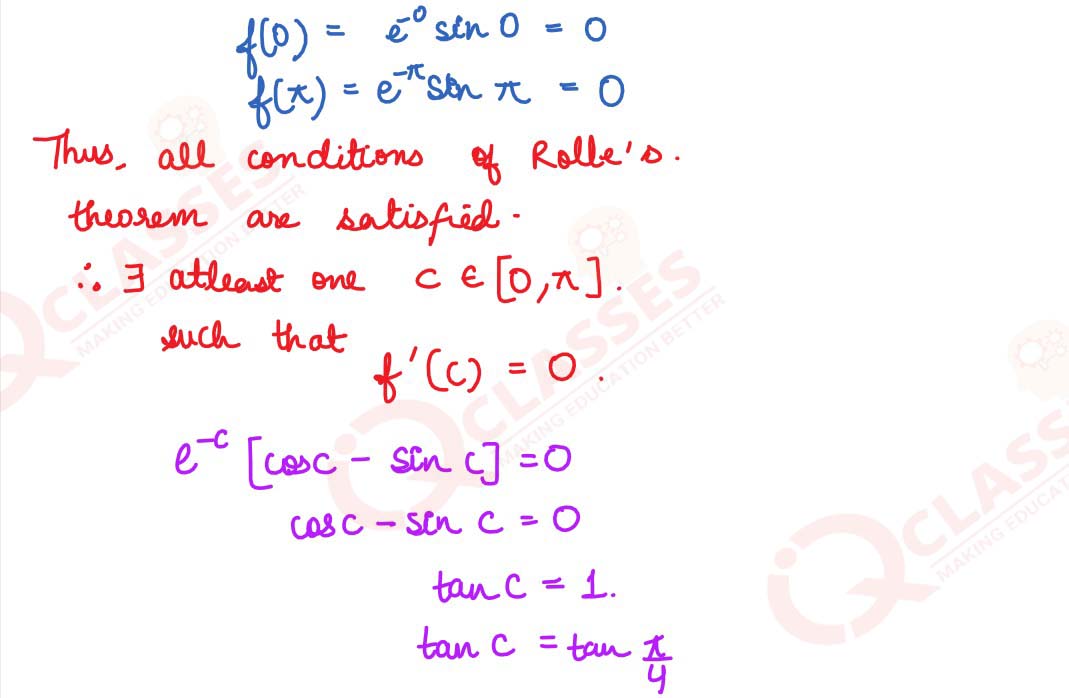

Q2
Find the value of constant 'k' so that the function f(x) defined as:
f(x)= f(x) =
is continuous at x=-1
solutions
|
x2-2x-3
/
x+1
,x ≠ -1
|
| k,x=-1 |
solutions

2019
Q1
(a) Show that the functionf(x) = |x—4|, x ∈ R is continuous, but not differentiable at x = 4.
OR
(b) Verify the Lagrange's mean value theorem for the ftnction:
f(x)=x+ 1/x in the interval [1, 3]
solutions




OR
(b) Verify the Lagrange's mean value theorem for the ftnction:
f(x)=x+ 1/x in the interval [1, 3]
solutions





Q2
Using L'Hospital's Rule, evaluate: limx->0
solutions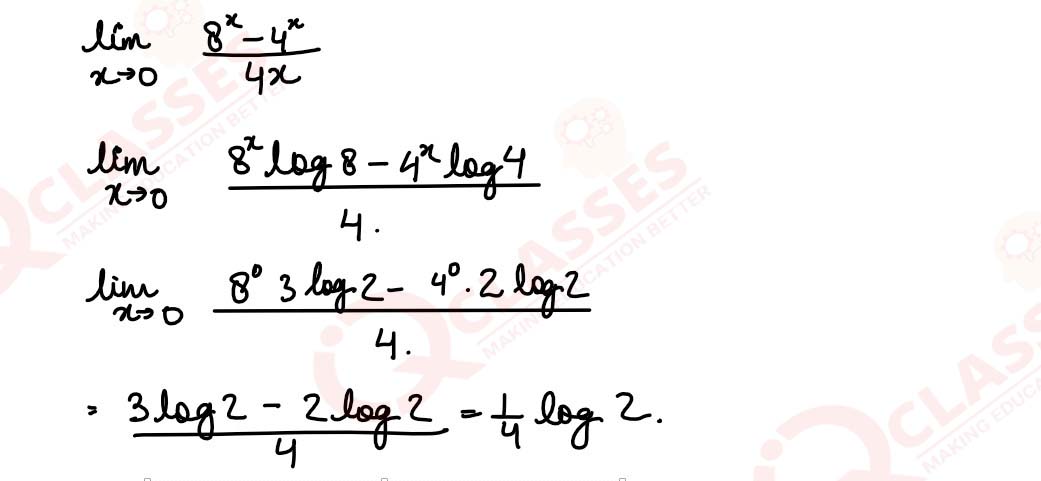
8x -4x
/
4x
solutions
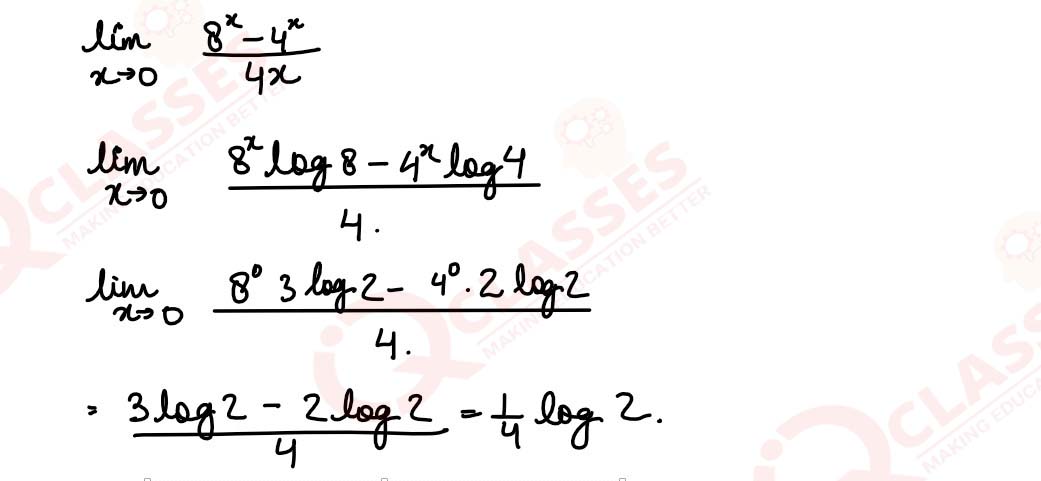
Q3
f(x)=
solutions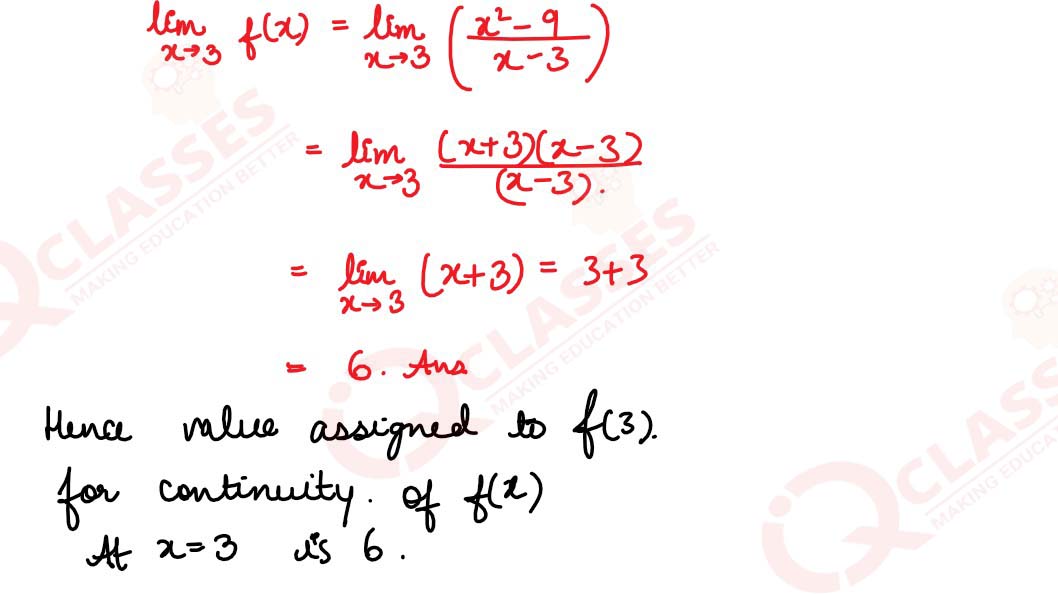
x2 -9
/
x-3
is not defined at x = 3. What value should be assigned to f(3) for
continuity of f(x) at x = 3?
solutions
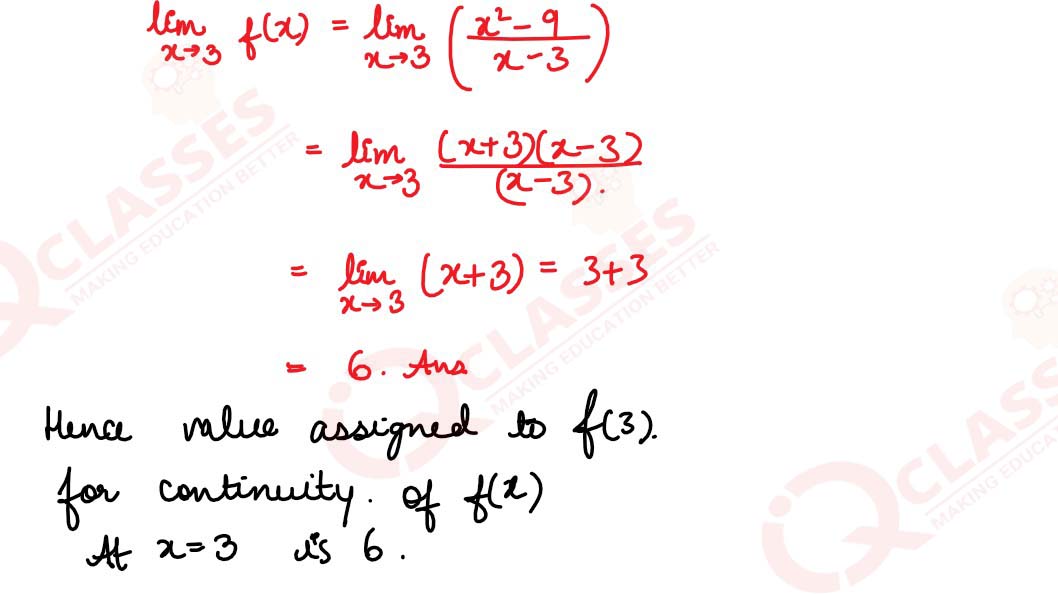
2020
Q1
Using L' Hospital's rule, evaluate:
limx->0
solutions
limx->0
x ex - log (1+x)
/
x2
solutions

Q2
Verify Rolle's theorem for the function, f (X) = —1 + cos X in the interval [O, 2 π]
solutions

solutions


Differentiation
2016
Q1
If log y = tan-1 x prove that:
(1 + x2)
solutions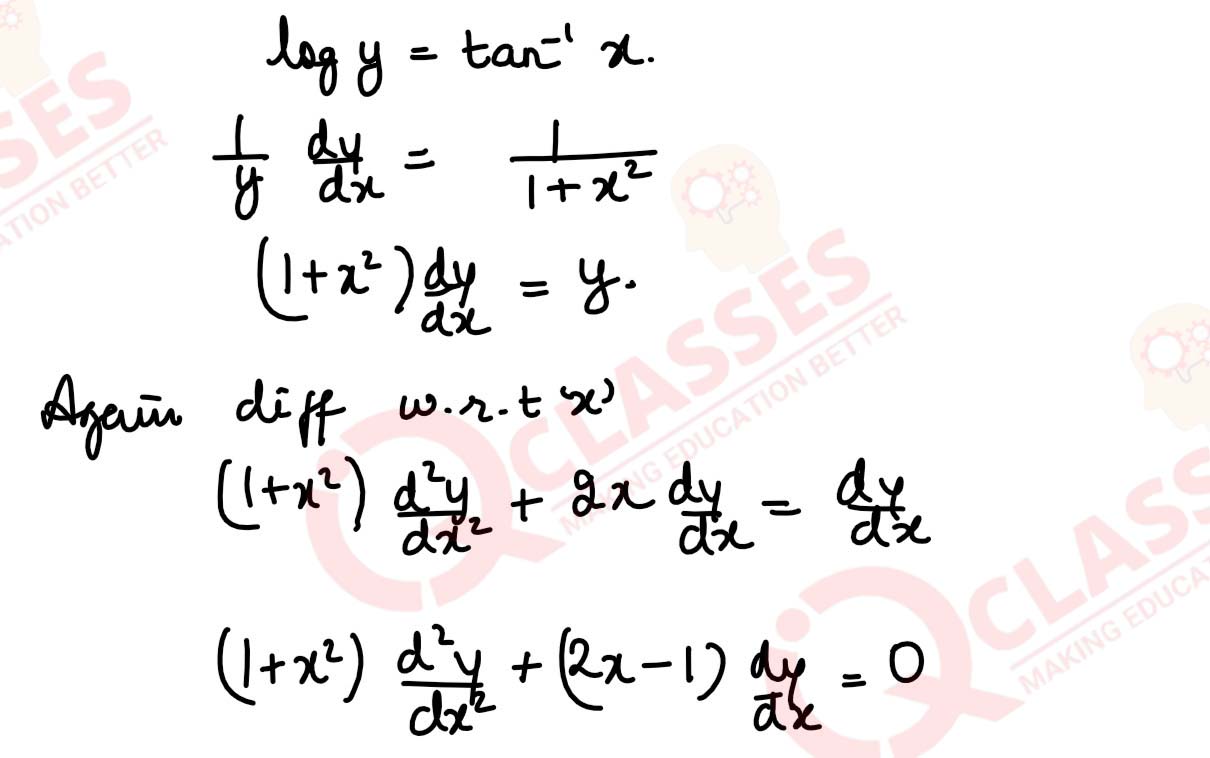


(1 + x2)
d2y
/
dx2
+ (2x - 1)
dy
/
dx
= 0
solutions
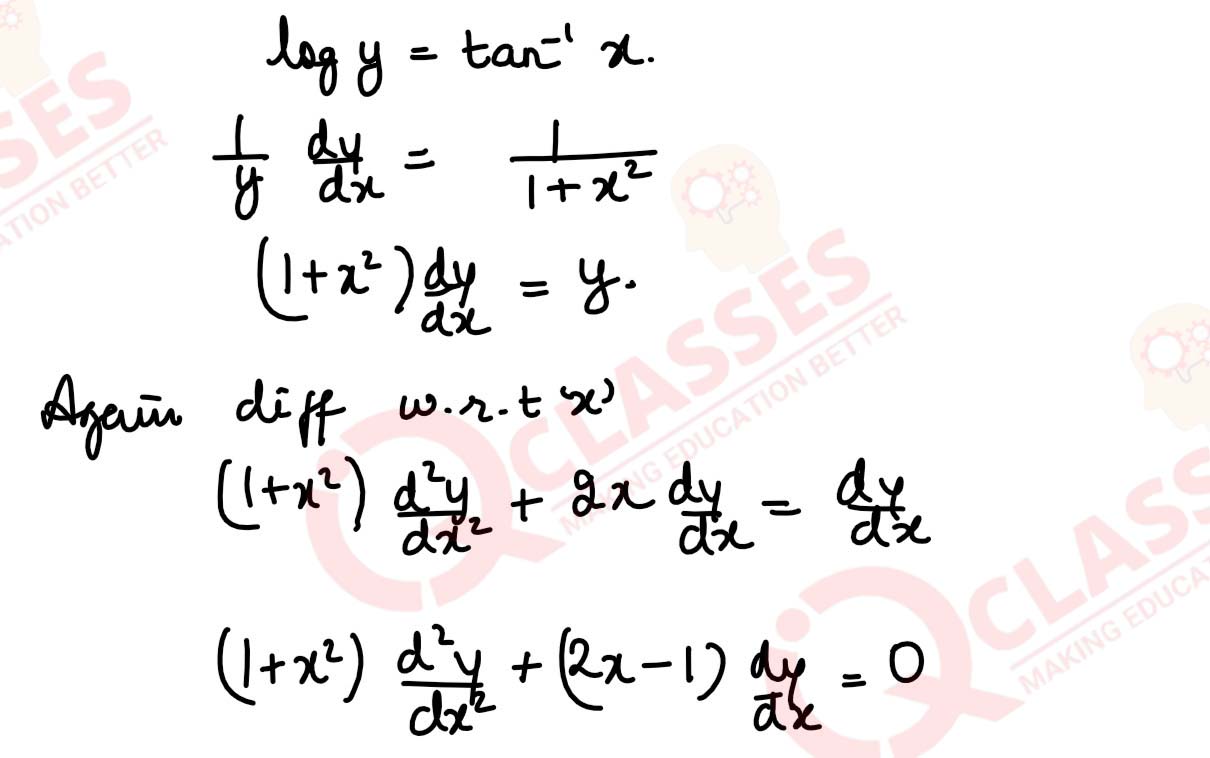


2017
Q2
If y = cos (sinx), show that :
solutions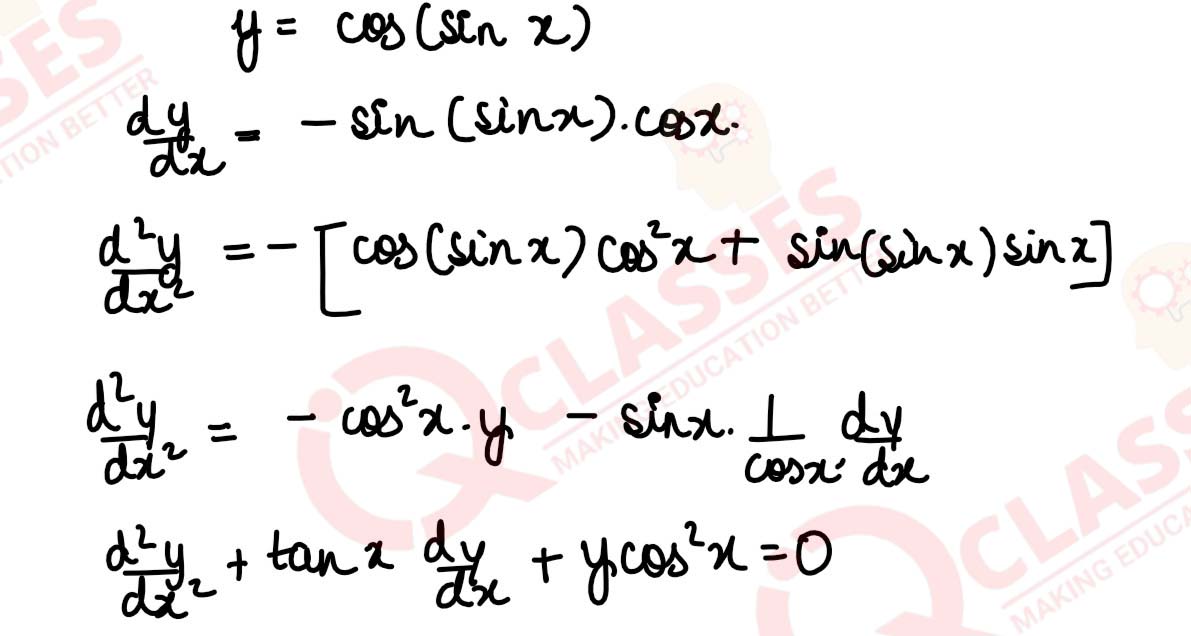
d2y
/
dx2
+ tan x
dy
/
dx
+ y cos2x = 0
solutions
2018
Q3
If x = tan(
solutions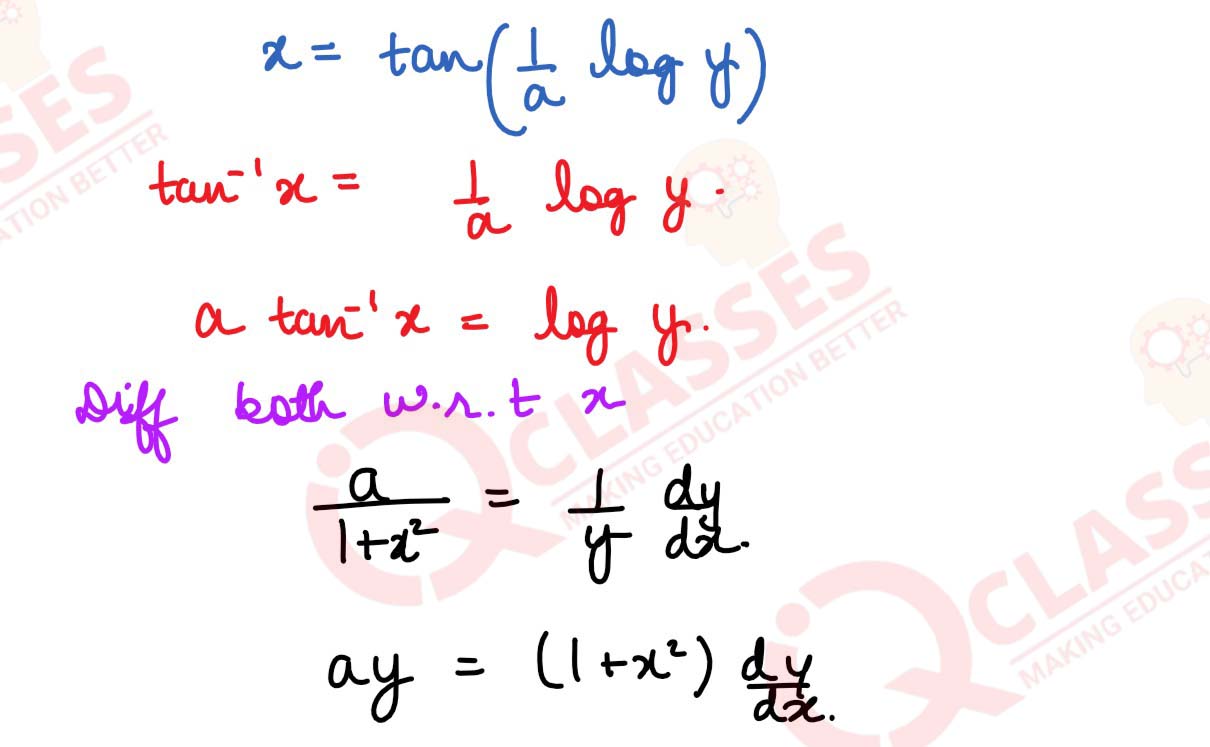
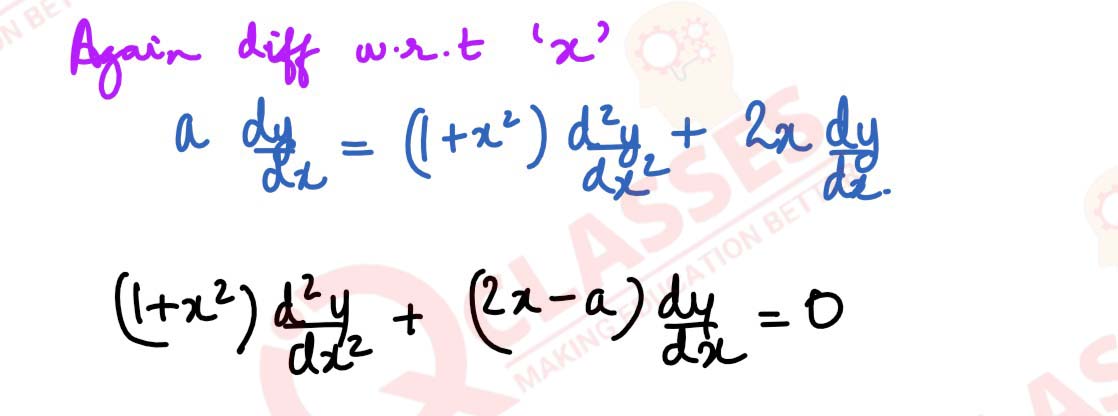
1
/
a
logy), prove that ( 1+ x2)
d2y
/
dx2
+ (2x-a)
dy
/
dx
= 0
solutions
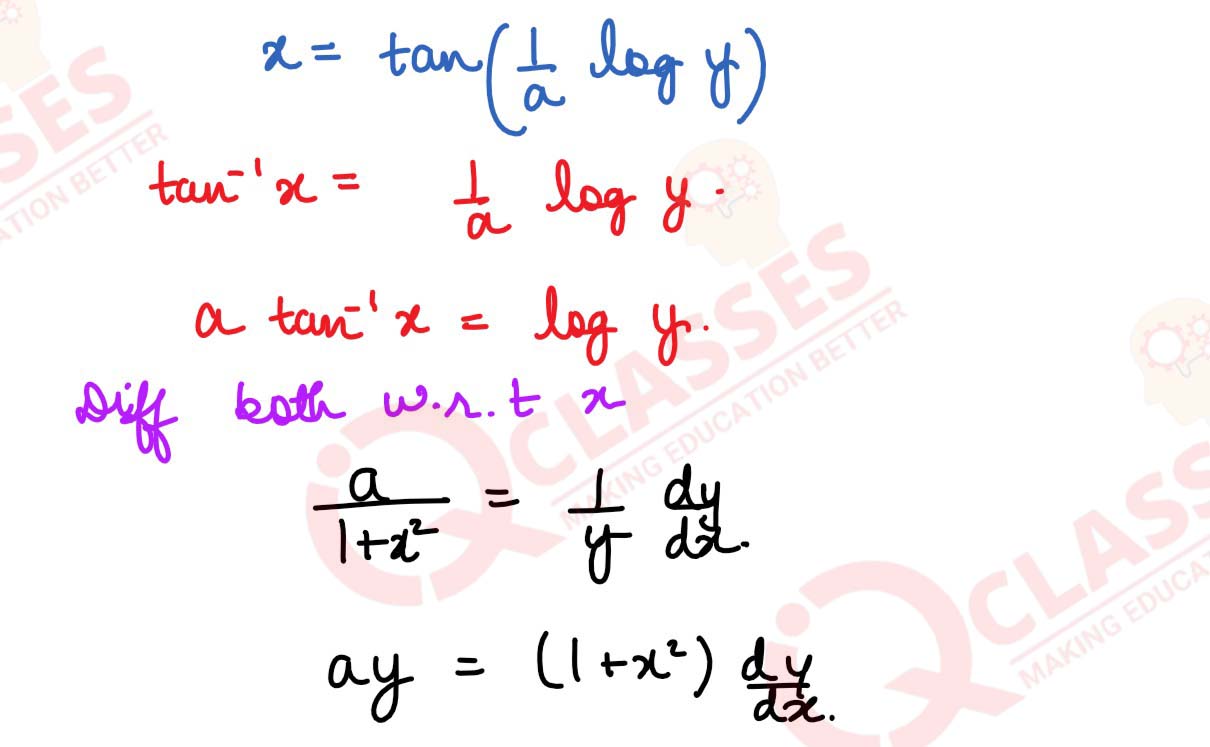
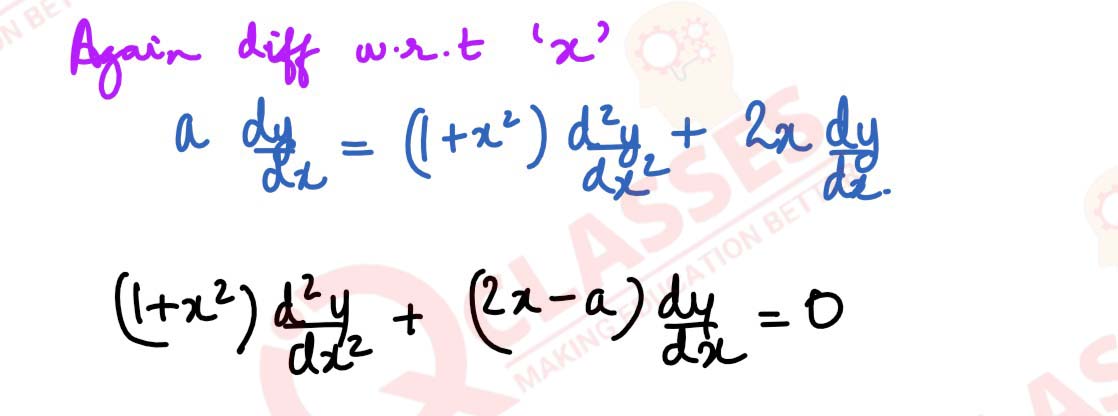
2019
Q4
If y = esin-1x
and z = e-cos-1x, prove that
solutions
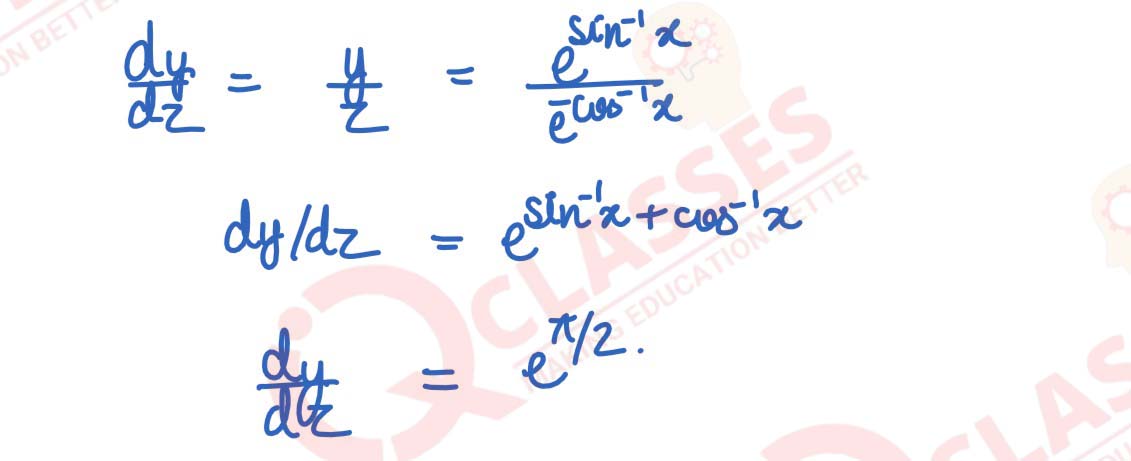
dy
/
dx
= eπ/2
solutions

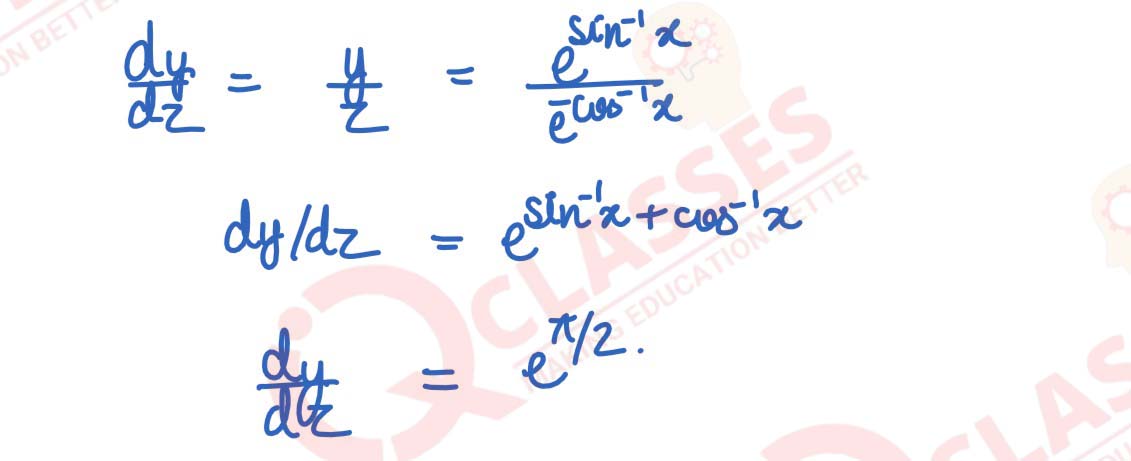
2020
Q5
If y = em sin-1x, prove that:
(1 - x2)
solutions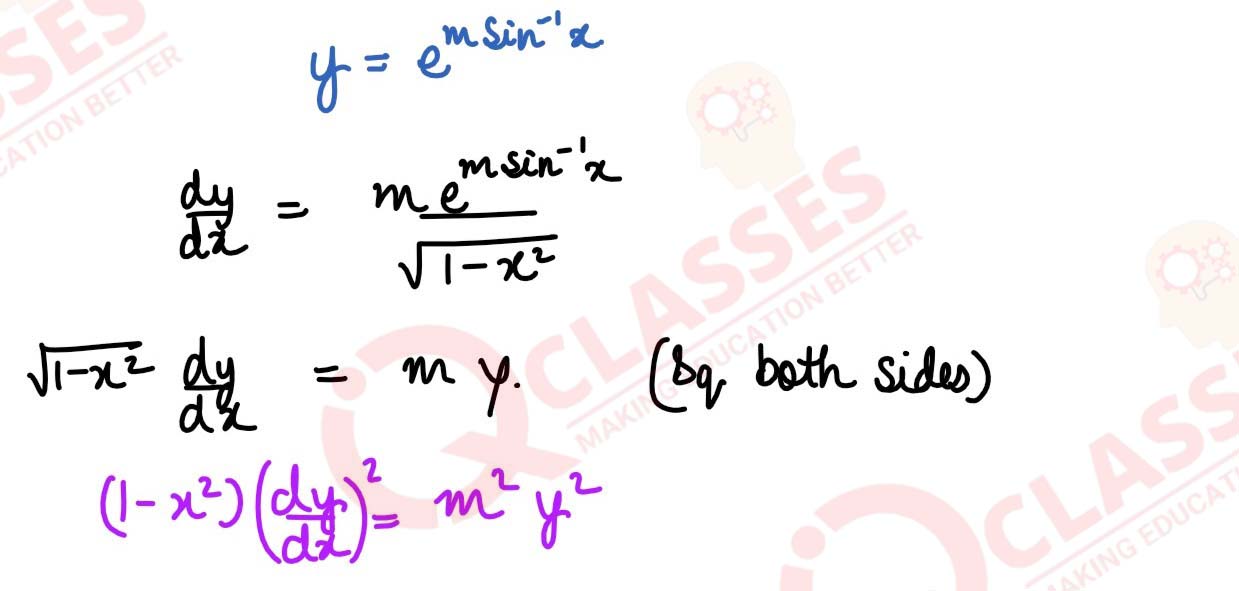
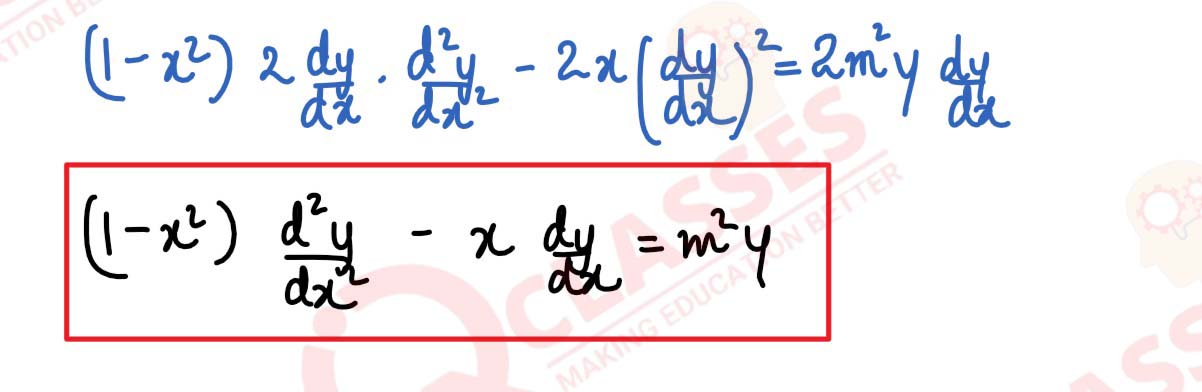
(1 - x2)
d2y
/
dx2
- x
dy
/
dx
= m2y
solutions
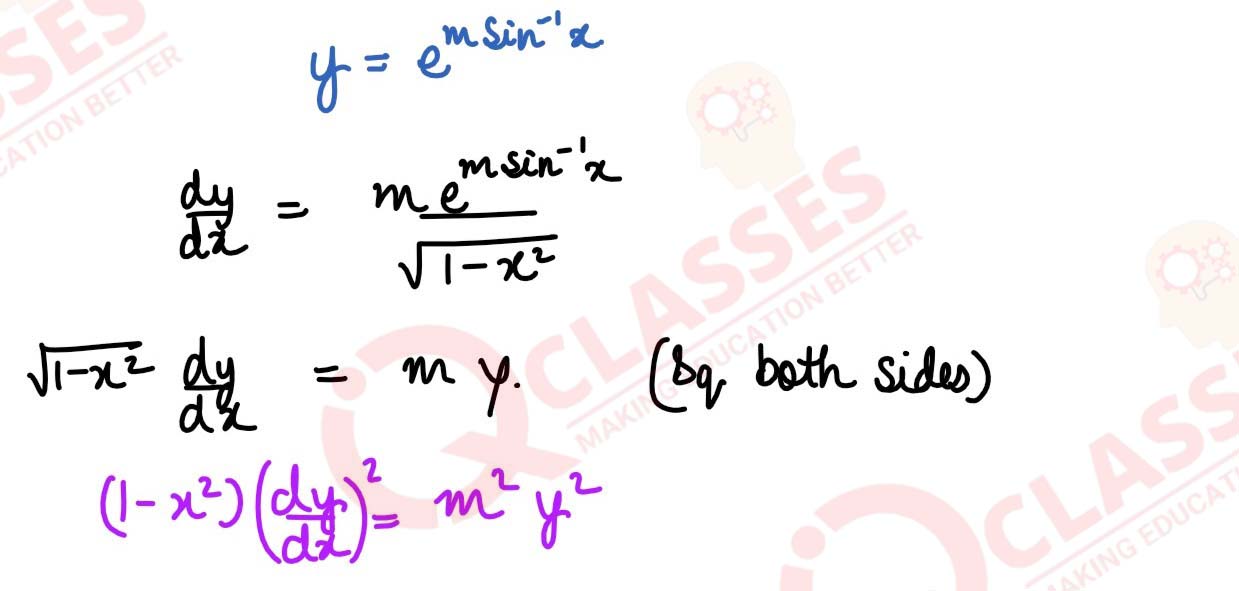
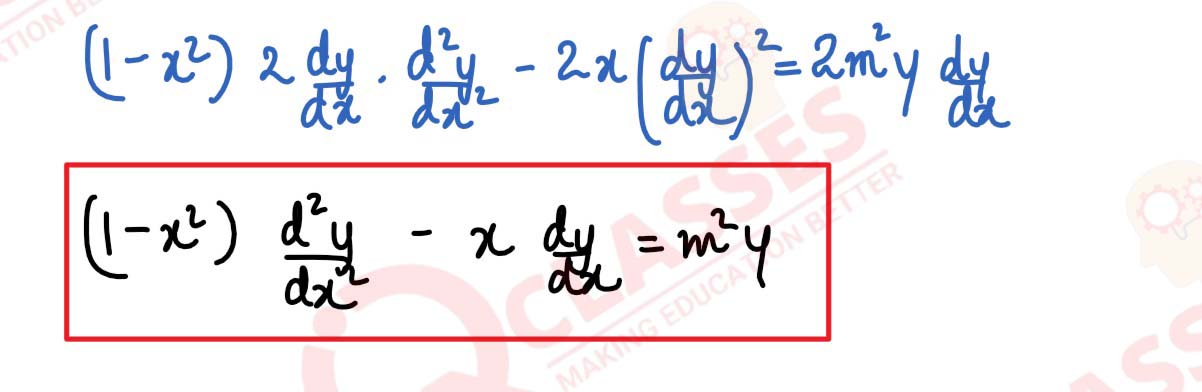
Q6
Find
solutions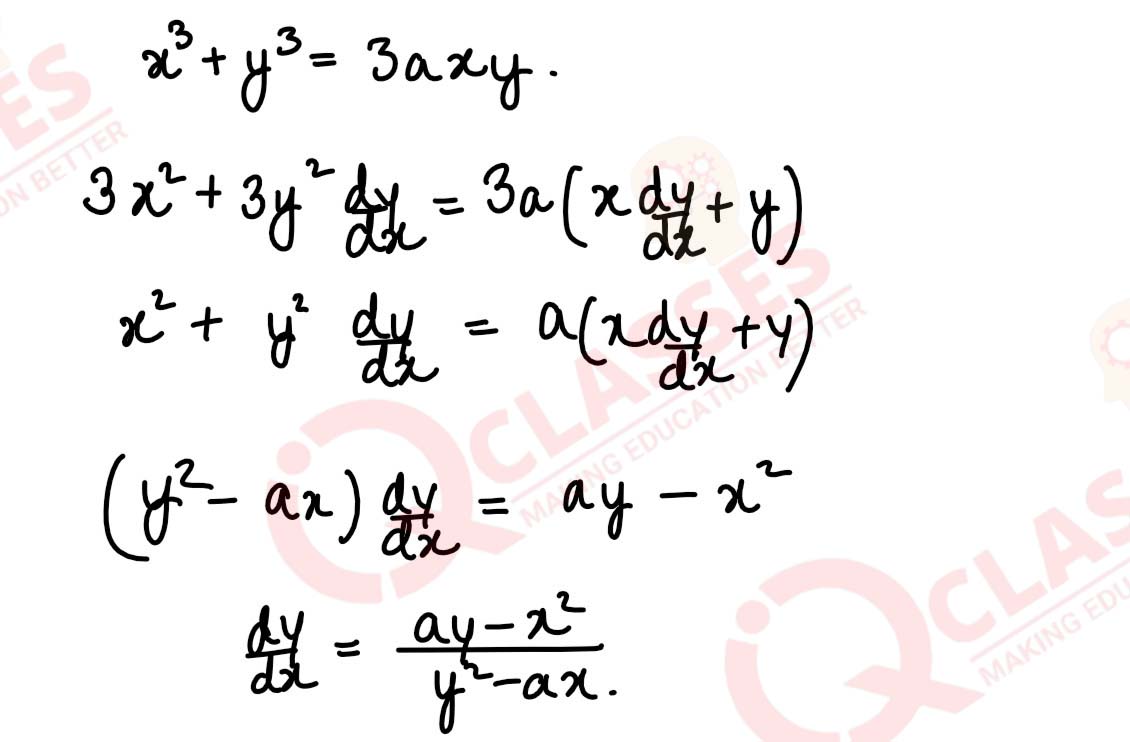
dy
/
dx
if x3 + y3 = 3axy
solutions
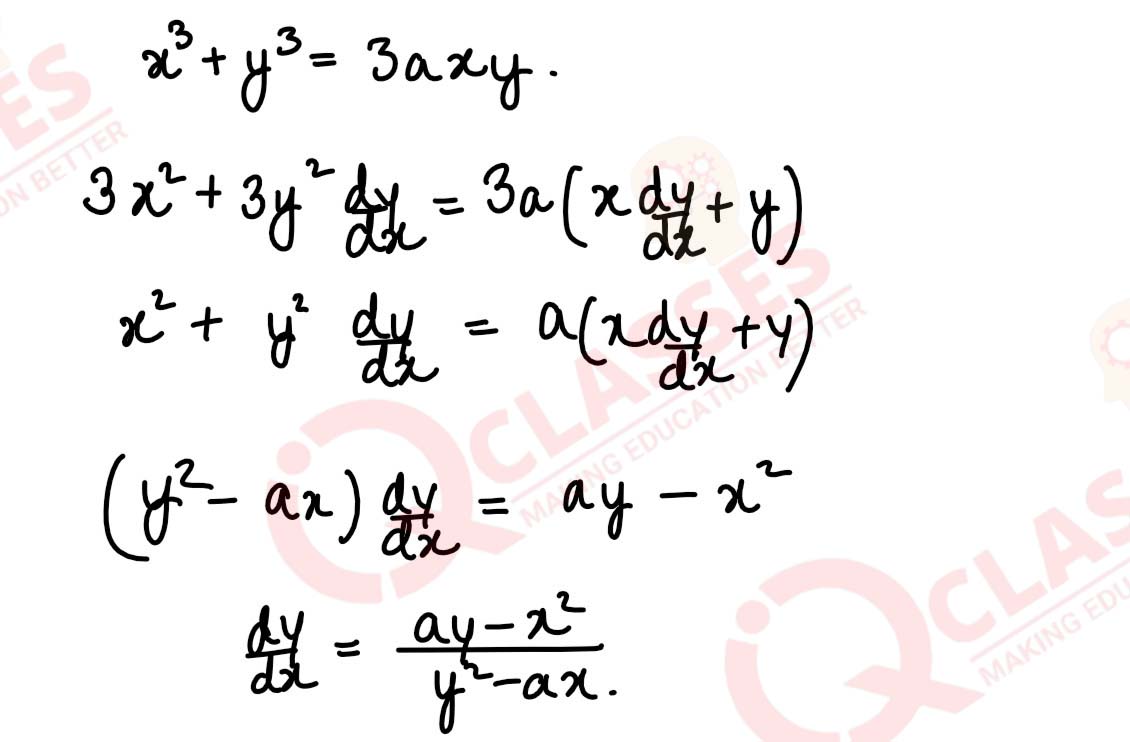


Add a comment