Class 12 Maths ISC Linear Programming Board Questions
Here we provide Class 12 Maths important notes,board questions and predicted questions with Answers for chapter Linear Programming. These important notes,board questions and predicted questions are based on ISC board curriculum and correspond to the most recent Class 12 Maths syllabus. By practising these Class 12 materials, students will be able to quickly review all of the ideas covered in the chapter and prepare for the Class 12 Board examinations.
2020
Q1
A company uses three machines to manufacture two types of shirts, half sleeves and full
sleeves. The number of hours required per week on machine M1 , M2 and
M3 for one shirt
of each type is given in the following table :

None of the machines can be in operation for more than 40 hours per week. The profit on each half sleeve shirt is ₹1 and the profit on each full sleeve shirt is ₹1•50. How many of each type of shirts should be made per week to maximise the company's profit?
solutions
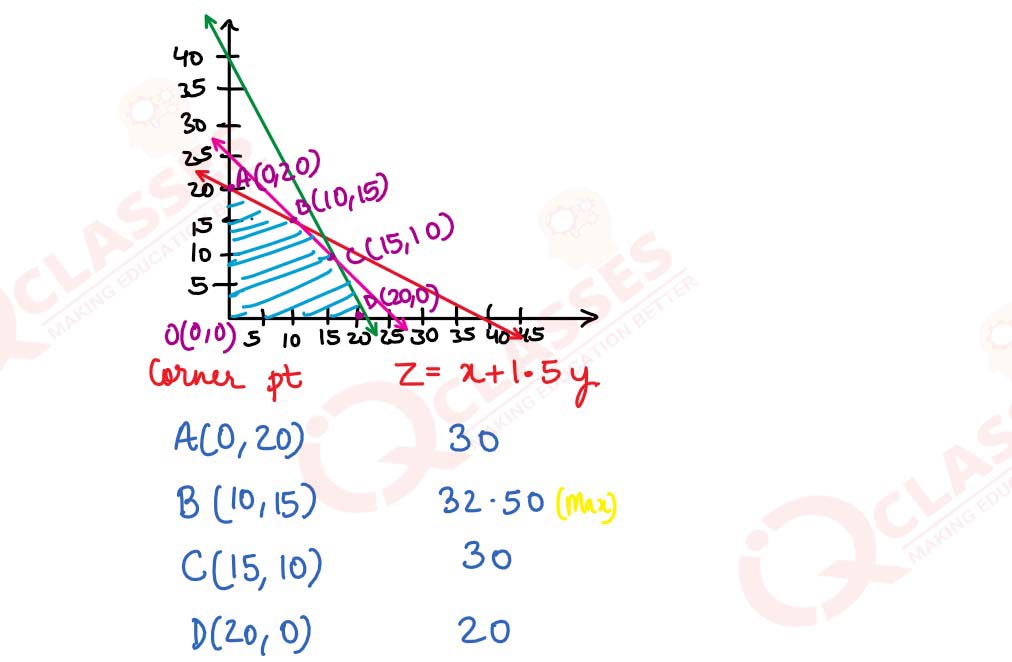


None of the machines can be in operation for more than 40 hours per week. The profit on each half sleeve shirt is ₹1 and the profit on each full sleeve shirt is ₹1•50. How many of each type of shirts should be made per week to maximise the company's profit?
solutions



2016
Q1
A company manufactures two types of products A and 3. Each unit of A requires 3 grams of nickel and
1
gram of chromium, while each unit of 3 requires 1 gram of nickel and 2 grams of chromium. The firm
can
produce g grams of nickel and 8 grams of chromium. The profit is ₹40 on each unit of the product of
type A
and ₹50 on each unit of type B. How many units of each type should the company manufacture so as to
earn a maximum profit? use linear programming to find the solution.
solutions

solutions


2017
Q1
A farmer has a supply of chemical fertilizer of type A which contains nitrogen and 6% phosphoric
acid and of type 3 which contains 5% nitrogen and phosphoric acid. After the soil test, is found
that
at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The
fertilizer
of type A costs ₹5.00 per kg and the type 3 costs ₹8.00 per kg. Using Linear programming, find how
many
kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be
minimum. Find the feasible region in the graph.
solutions
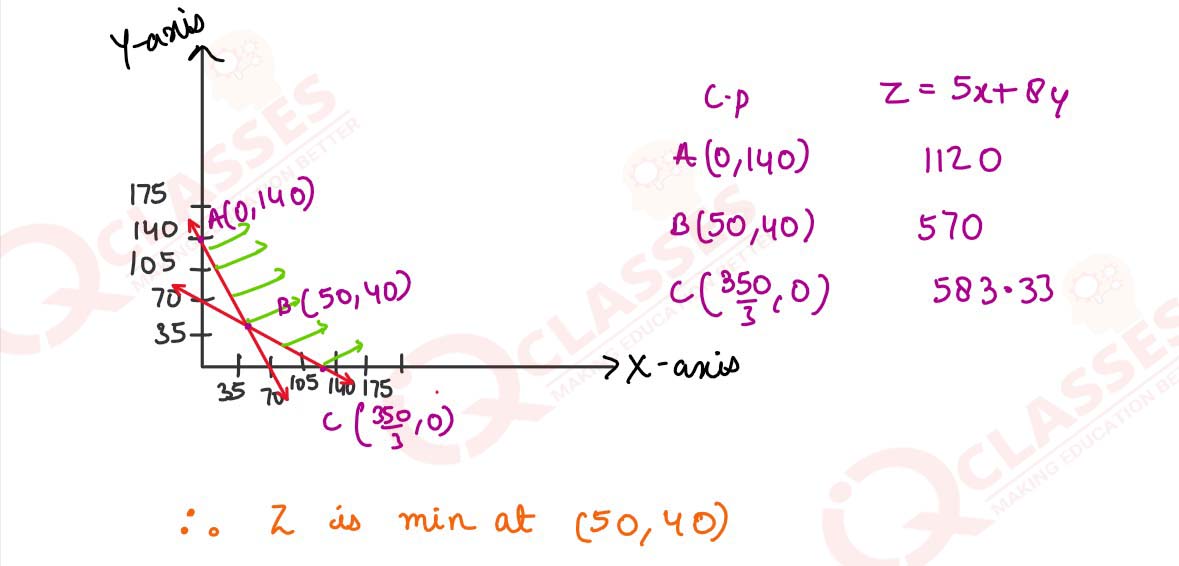

solutions



2018
Q1
A manufacturing company makes two types of teaching aids A and 3 of Mathematics for Class X. Each
type of A requires g labour hours for fabricating and 1 labour hour for finishing. Each type of 3
requires 12
labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the
maximum
labour hours available per week are 180 and 30 respectively. The company makes a profit of ₹80 on
each
piece of type A and ₹120 on each piece of type B. How many pieces of type A and type B should be
manufactured per week to get a maximum profit? Formulate this as Linear Programming Problem and
solve it. Identify the feasible region from the rough sketch.
solutions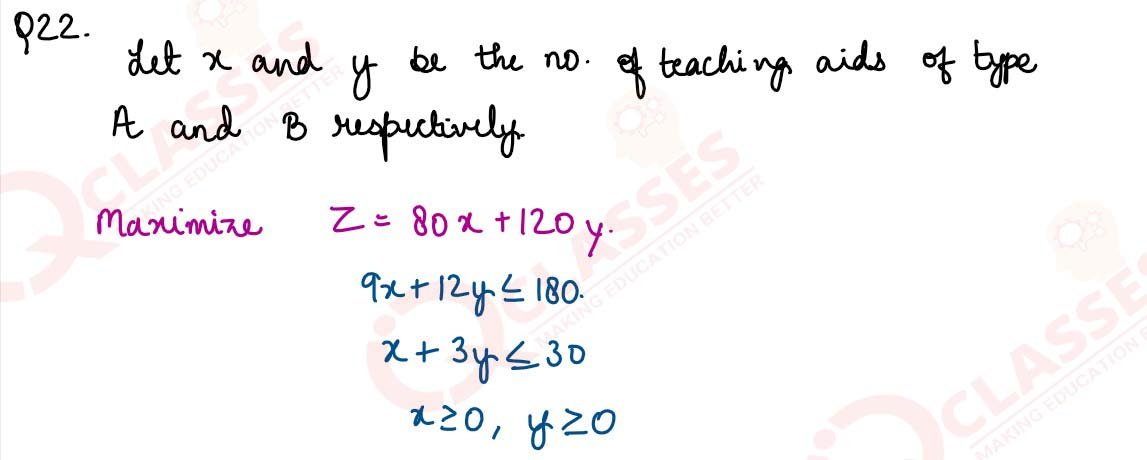
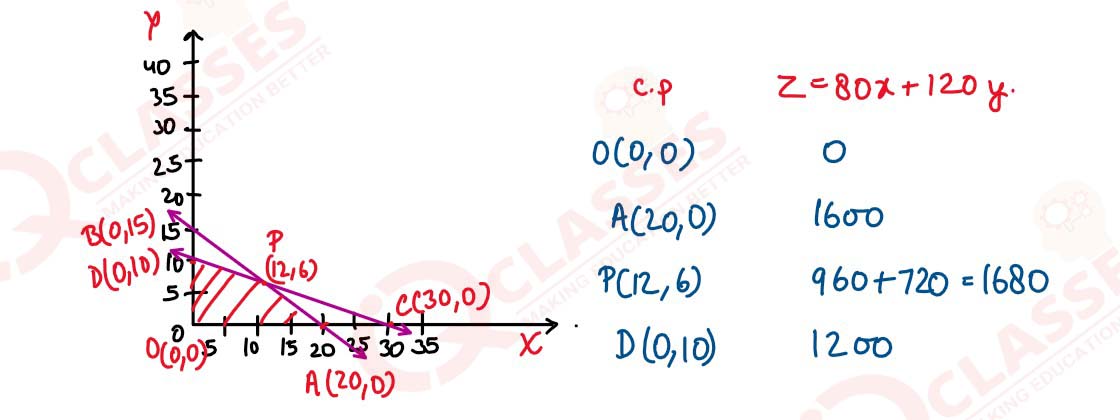

solutions
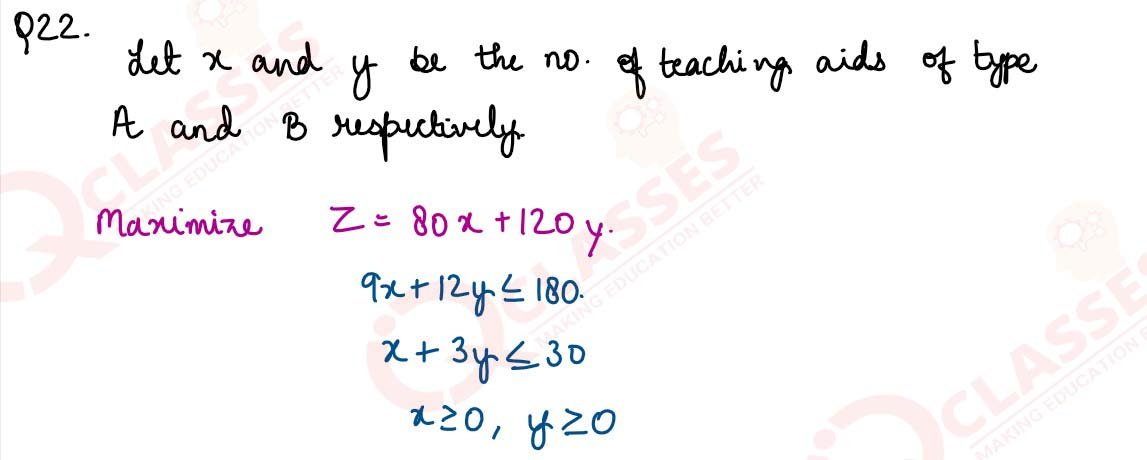


2019
Q1
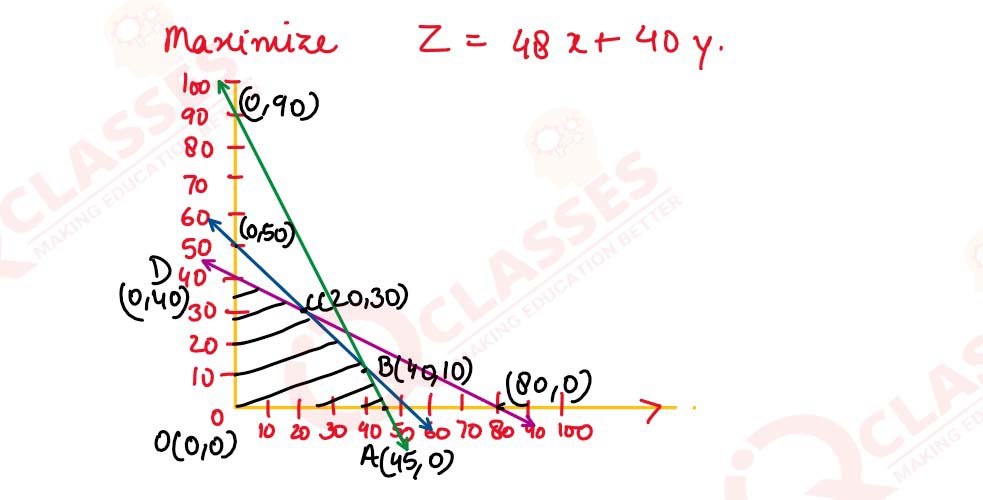
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is
used
to produce product A and product 3. Each unit of product A requires 2, 1 and 1 running feet and each
unit of
product 3 requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If
product A is
sold for ₹48 per unit and product 3 is sold for ₹40 per unit, how many units of product A and
product B
should be produced and sold by the carpenter, in order to obtain the maximum gross income?
Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible
region in
the graph.
solutions


solutions





Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment