Class 12 CBSE Maths Linear Programming Important Questions
Here we provide Class 12 Maths important questions,board questions and predicted questions with Answers for chapter Linear Programming. These important notes,board questions and predicted questions are based on CBSE board curriculum and correspond to the most recent Class 12 Maths syllabus. By practising these Class 12 materials, students will be able to quickly review all of the ideas covered in the chapter and prepare for the Class 12 Board examinations.
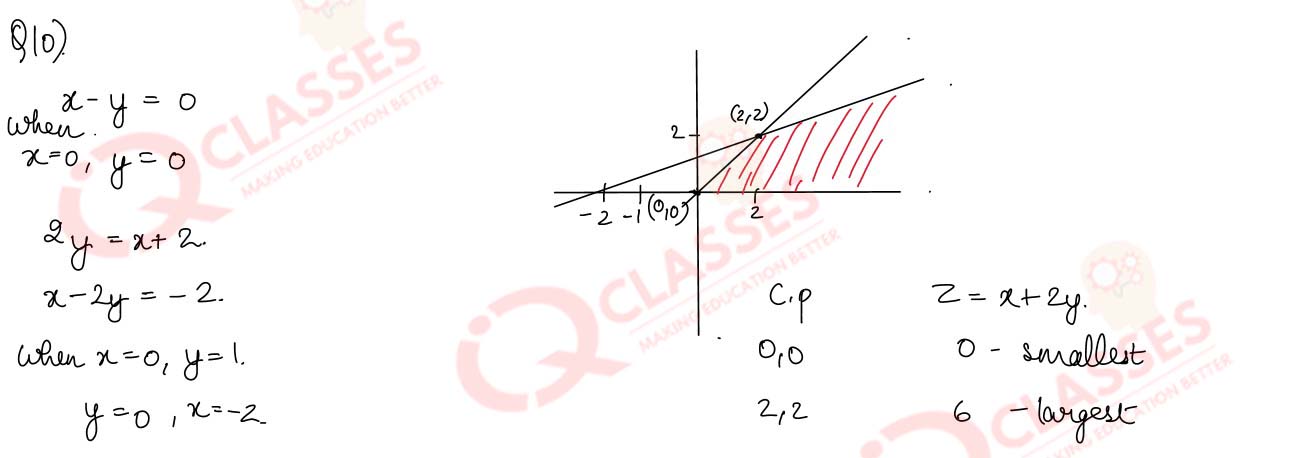
Q(1)
Maximize Z = x + 2y subject to the constraints
x - y ≥ 0, 2y≤x + 2, x ≥ 0, y ≥ 0.
Solution
Q(2)
Maximize and minimize Z = 5x + 10y subject to the constraints
x + 2y≤120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0
Solution


Q(3)
A furniture dealer deals in only two items—tables and chairs. He has ₹10000 to invest and a space to
store atmost 60 pieces. A table costs him ₹500 and a chair costs him ₹100. He can sell a table at
₹550 and a chair at ₹115. Assume that he can sell all the items that he buys
- Formulate this problem as an L.P.P. so that he maximizes his profit.
- Draw the feasible region on a graph and clearly mention the corner points.
- Solve this problem using corner point method.
Solution


Q(4) A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of ₹80 on each piece of type A and ₹120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solution


Q(5) If a young man rides his motor cycle at 25 km per hour, he has to spend ₹2 per kilometre on petrol; if he rides at a faster speed of 40 km per hour, the petrol cost increases to ₹5 per kilometre. He has ₹100 to spend on petrol and wishes to find the maximum distance he can travel within one hour. Express this as a linear programming problem and then solve it.
Solution


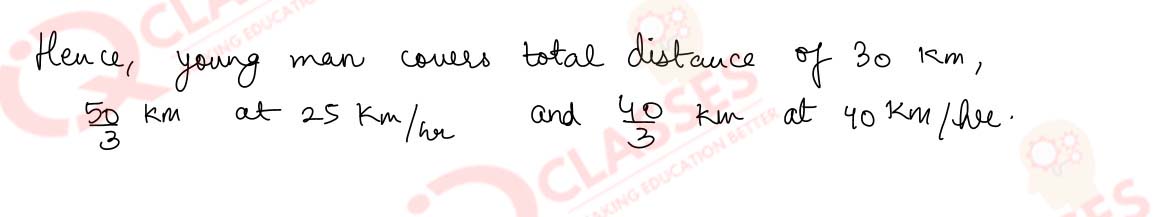
Q(6) A manufacturer makes two products, A and B. Product A sells at ₹200 each and takes 1/2 hour to make. Product B sells at ₹300 each and takes 1 hour to make. There is a permanent order for 14 units of product A and 16 units of product B. A working week consists of 40 hours of production and the weekly turnover must not be less than ₹10000. If the profit on each of product A is ₹20 and on product B is ₹30, then how many of each should be produced so that the profit is maximum? Also find the maximum profit.
Solution



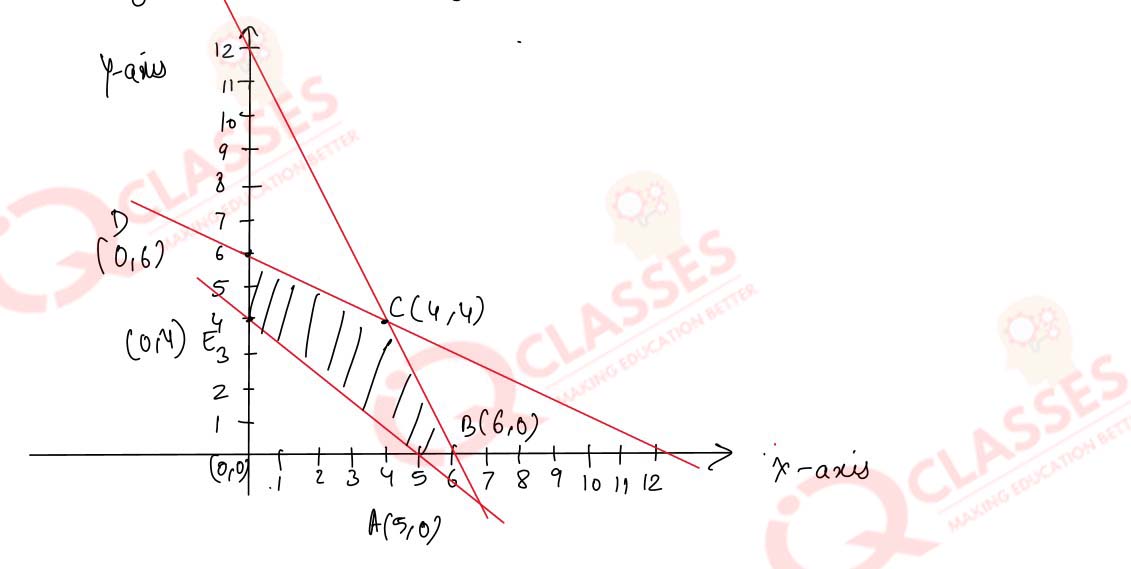
Q(7)
A manufacturer has three machines I, II and III installed in her factory. Machines I and II are
capable of being operated for atmost 12 hours whereas machine III must be operated atleast 5 hours a
day. She produces only two items M and N each requiring the use of all the three machines. The
number of hours required for producing 1 unit of each of M and N on the three machines are given in
the following table :
| Items | Number of hours required on machines | ||
|---|---|---|---|
| I | II | III | |
| M | 1 | 2 | 1 |
| N | 2 | 1 | 1.25 |
Solution

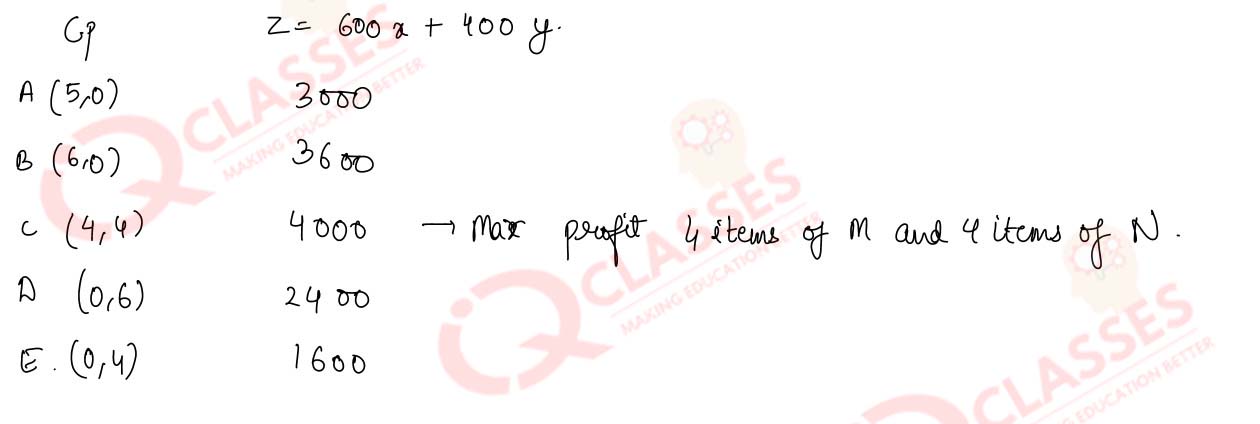
Q(8)
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of
food P contains 12 units of calcium, 4 units of iron, 6 units of cholestrol and 6 units of vitamin
A. Each packet of the same quantity of food Q contains 3 unit of calcium, 20 units of iron, 4 units
of cholestrol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460
units of iron and atmost 300 units of cholestrol.
- How many packets of each food should be used to minimize the amount of vitamin A? What is
the minimum amount of vitamin A?
- How many packets of each food should be used to maximize the amount of vitamin A in the
diet? What is the maximum amount of vitamin A?
Solution
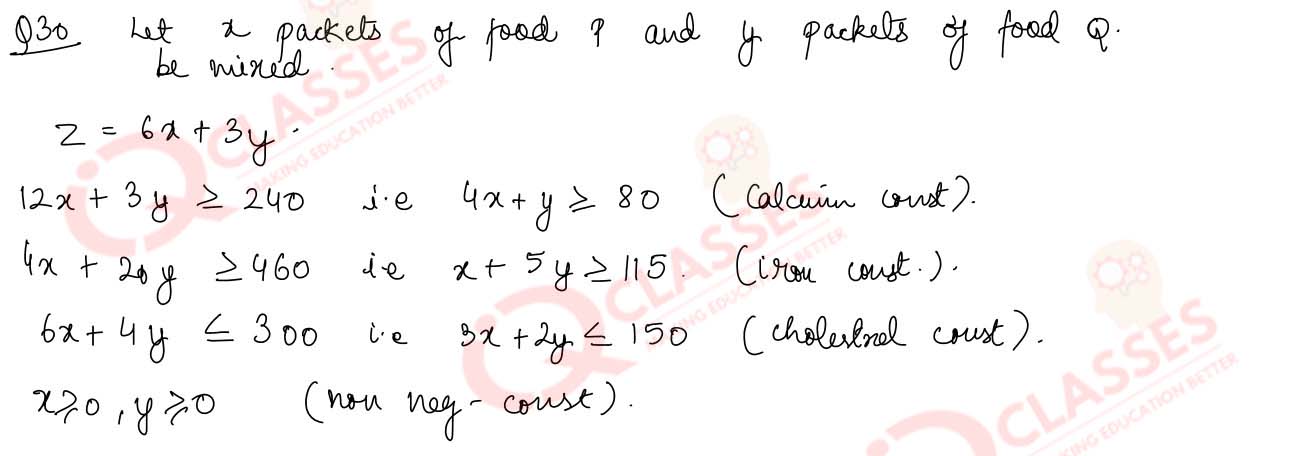


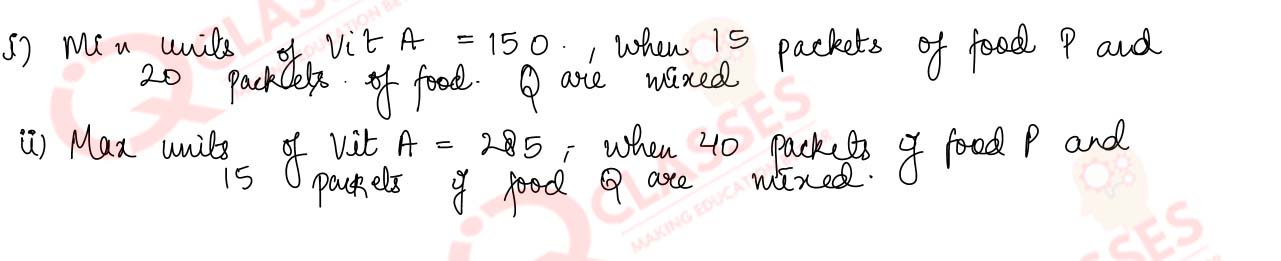
Q(9) A diet for a sick person must contain atleast 4000 units of vitamins, 50 units of minerals and 1400 units of calories. Two foods A and B are available at a cost of ₹4 and ₹3 per unit respectively. If one unit of A contains 200 units of vitamin, 1 unit of mineral and 40 units of calories, and one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 units of calories, then find what combination of foods should be used to have the least cost?
Solution


Q(10) A company manufactures three kinds of calculators: A, B and C in its two factories I and II. The company has got an order for manufacturing atleast 6400 calculators of kind A, 4000 of kind B and 4800 of kind C. The daily output of factory I is of 50 calculators of kind A, 50 calculators of kind B, and 30 calculators of kind C. The daily output of factory II is of 40 calculators of kind A, 20 of kind B and 40 of kind C. The cost per day to run factory I is ₹12,000 and of factory II is ₹15,000. How many days do the two factories have to be in operation to produce the order with the minimum cost? Formulate this problem as an LPP and solve it graphically
Solution



Q(11) A catering agency has two kitchens to prepare food at two places A and B. From these places 'Mid-day meal' is to be supplied to three different schools situated at P, Q, R. The monthly requirements of the schools are respectively 40, 40 and 50 food packets. A packet contains lunch for 100 students. Preparing capacity of kitchens A and B are 60 and 70 packets per month respectively. The trnsportation cost per packet from the kitchens to schools is given below :
| Transportation cost per packet (in ₹) | ||
|---|---|---|
| To | From | |
| A | B | |
| P | 5 | 4 |
| Q | 4 | 2 |
| R | 3 | 5 |
Solution






Reach Us
SERVICES
- ACADEMIC
- ON-LINE PREPARATION
- FOUNDATION & CRASH COURSES
CONTACT
B-54, Krishna Bhawan, Parag Narain Road,
Near Butler Palace Colony Lucknow
Contact:+918081967119

Add a comment