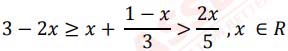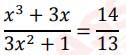Maximum Marks: 80
Time allowed: Two and half hours
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown, and must be done on the same sheet as
the rest of the answer.
Omission of essential working will result in loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ]
Mathematical tables are provided.
Section-A
(Attempt all questions from this Section.)
Question 1
Choose the correct answers to the questions from the given options.
(Do not copy the questions, write the correct answers only.)
(i) If A = 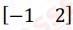 and B =
and B = 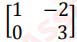
Which of the following operation is
possible?
(a) A – B
(b) A + B
(c) AB
(d) BA
Solution
View
Solution
(ii) If 𝑥
2 + 𝑘𝑥 + 6 = (𝑥 − 2 )(𝑥 − 3) for all values of x, then the value of k is:
(a) – 5
(b) – 3
(c) – 2
(d) 5
Solution
View Solution
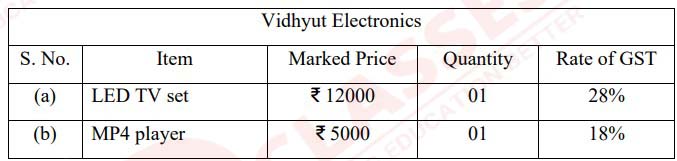
(iii) A retailer purchased an item for ₹1500 from a wholesaler and sells it to a customer
at 10% profit. The sales are intra-state and the rate of GST is 10%. The amount of
GST paid by the customer:
(a) ₹15
(b) ₹30
(c) ₹150
(d) ₹165
Solution
View
Solution
(iv) If the roots of equation 𝑥
2 − 6𝑥 + 𝑘 = 0 are real and distinct, then value of k is:
(a) > –9
(b) > –6
(c) < 6
(d) < 9
Solution
View Solution
(v) Which of the following is/are an Arithmetic Progression (A.P.)?
1. 1, 4, 9, 16,……….
2. √3, 2√3, 3√3, 4√3,………
3. 8, 6, 4, 2,………
(a) only 1.
(b) only 2.
(c) only 2. and 3.
(d) all 1., 2. and 3.
Solution
View
Solution
(vi) The table shows the values of x and y, where x is proportional to y.
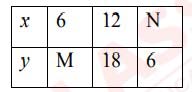
What are the values of M and N?
(a) M = 4, N = 9
(b) M = 9, N = 3
(c) M = 9, N = 4
(d) M = 12, N =0
Solution
View
Solution
(vii) In the given diagram, ∆ ABC ~ ∆ PQR and  The value of AB : PQ is:
The value of AB : PQ is:
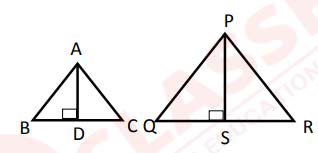
(a) 8 : 3
(b) 3 : 5
(c) 3 : 8
(d) 5 : 8
Solution
View
Solution
(viii) A right angle triangle shaped piece of hard board is rotated completely about its
hypotenuse, as shown in the diagram. The solid so formed is always:
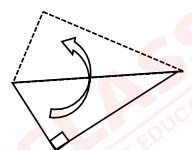
1. a single cone
2. a double cone
Which of the statement is valid?
(a) only 1.
(b) only 2.
(c) both 1. and 2.
(d) neither 1. nor 2.
Solution
View
Solution
(ix) Event A: The sun will rise from east tomorrow.
Event B: It will rain on Monday.
Event C: February month has 29 days in a leap year.
Which of the above event(s) has probability equal to 1?
(a) all events A, B and C
(b) both events A and B
(c) both events B and C
(d) both events A and C
Solution
View
Solution
(x) The three vertices of a scalene triangle are always equidistant from a fixed point.
The point is:
(a) Orthocentre of the triangle.
(b) Incentre of the triangle.
(c) Circumcentre of the triangle.
(d) Centroid of the triangle.
Solution
View
Solution
(xi) In a circle with radius R, the shortest distance between two parallel tangents is equal
to∶
(a) R
(b) 2R
(c) 2πR
(d) πR
Solution
View
Solution
(xii) An observer at point E, which is at a certain distance from the lamp post AB, finds
the angle of elevation of top of lamp post from positions C, D and E as α, β and γ.
It is given that B, C, D and E are along a straight line.
Which of the following condition is satisfied?
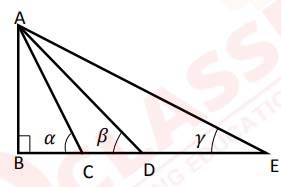
(a) tanα > tan β
(b) tan β < tan γ
(c) tan γ > tan α
(d) tan α < tan β
Solution
View
Solution
(xiii) 1. Shares of company A, paying 12%, ₹100 shares are at ₹80.
2. Shares of company B, paying 12%, ₹100 shares at ₹100.
3. Shares of company C, paying 12%, ₹100 shares are at ₹120.
Shares of which company are at premium?
(a) Company A
(b) Company B
(c) Company C
(d) Company A and C
Solution
View
Solution
(xiv) Which of the following equation represent a line passing through origin?
(a) 3x – 2y + 5 = 0
(b) 2x – 3y = 0
(c) x = 5
(d) y = –6
Solution
View
Solution
(xv) For the given 25 variables: 𝒙𝟏 , 𝒙𝟐 , 𝒙𝟑 … … … … … . 𝒙𝟐𝟓
Assertion (A): To find median of the given data, the variate needs to be arranged
in ascending or descending order.
Reason (R): The median is the central most term of the arranged data.
(a) A is true, R is false
(b) A is false, R is true
(c) both A and R are true
(d) both A and R are false
Solution
View
Solution
Question 2
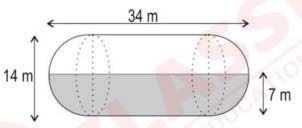
(i) Shown below is a horizontal water tank composed of a cylinder and two
hemispheres. The tank is filled up to a height of 7 m. Find the surface area of the
tank in contact with water. Use π = 22/7
(ii) In a recurring deposit account for 2 years, the total amount deposited by a person is
₹ 9600. If the interest earned by him is one-twelfth of his total deposit, then find:
(a) the interest he earns.
(b) his monthly deposit.
(c) the rate of interest.
(iii) Find:
(a) (sin 𝜃 + 𝑐𝑜𝑠𝑒𝑐 𝜃)
2
(b) (𝑐𝑜𝑠 𝜃 + 𝑠𝑒𝑐 𝜃)
2
Using the above results prove the following trigonometry identity.
(sin 𝜃 + 𝑐𝑜𝑠𝑒𝑐 𝜃)
2 + (cos 𝜃 + sec 𝜃)
2 = 7 + 𝑡𝑎𝑛2𝜃 + 𝑐𝑜𝑡2𝜃
Solution
View
Solution
Question 3
Section-B
(Attempt any four questions from this Section.)
Question 4
(i) If A =
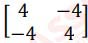 find A
2
. If A
2 = p A, then find the value of p
find A
2
. If A
2 = p A, then find the value of p
(ii) Solve the given equation x
2 − 4x − 2 = 0 and express your answer correct to two places
of decimal.
(You may use mathematical tables for this question).
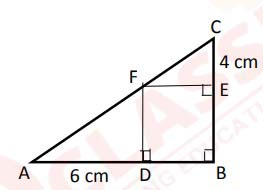
(iii) In the given diagram, ∆ABC is right angled at B. BDFE is a rectangle.
AD = 6 cm, CE = 4 cm and BC = 12 cm
(a) prove that ∆ADF ~∆FEC
(b) prove that ∆ADF ~∆ABC
(c) find the length of FE
(d) find area ∆ADF : area ∆ABC
Solution
View
Solution
Question 5
Question 6
(i) There are three positive numbers in a Geometric Progression (G.P.) such that:
(a) their product is 3375
(b) the result of the product of first and second number added to the product of second and
third number is 750.
Find the numbers.
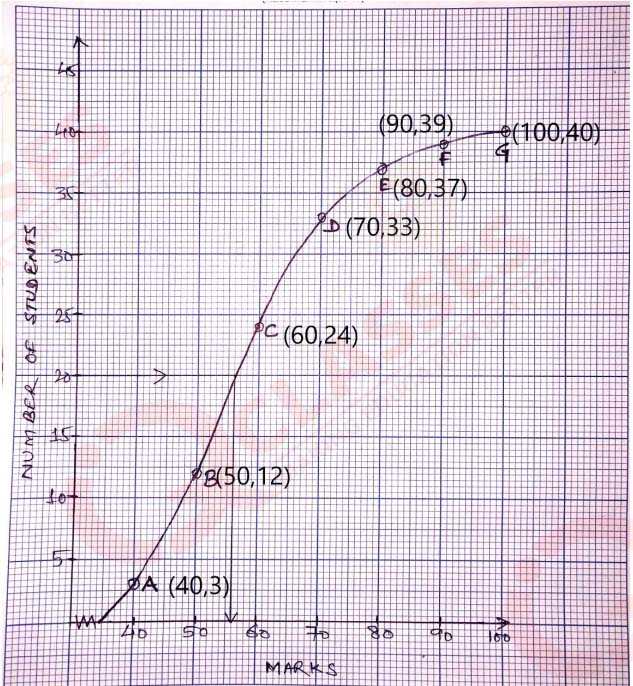
(ii) The table given below shows the ages of members of a society.
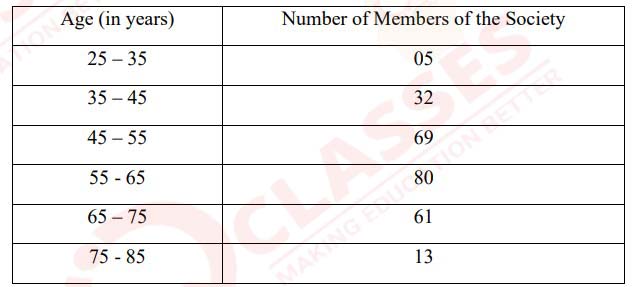
Use graph sheet for this question.
Take 2cm = 10 years along one axis and 2cm=10 members along the other axis.
(a) Draw a histogram representing the above distribution.
(b) Hence find the modal age of the members
(iii) A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of
the cylindrical part are 7 m each and the total height of the tent is 14 m. Find the:
(a) quantity of air contained inside the tent.
(b) radius of a sphere whose volume is equal to the quantity of air inside the tent.
Use 𝜋 =
22/
7
Solution
View
Solution
Question 7
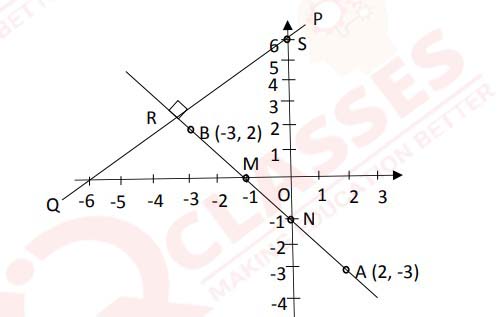
(i) The line segment joining A(2,-3) and B(-3, 2) is intercepted by the 𝑥-axis at the point M
and the y axis at the point N. PQ is perpendicular to AB produced at R and meets the y- axis
at a distance of 6 units from the origin O, as shown in the diagram, at S. Find the:
(a) coordinates of M and N
(b) coordinates of S
(c) slope of AB.
(d) equation of line PQ
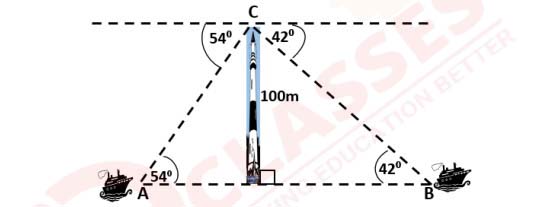
(ii) The angle of depression of two ships A and B on opposite sides of a light house of height
100m are respectively 42o
and 54o
. The line joining the two ships passes through the foot
of the lighthouse.
(a) Find the distance between the two ships A and B.
(b) Give your final answer correct to the nearest whole number.
(Use mathematical tables for this question)
Solution
View
Solution
Question 8
(i) Solve the following inequation write the solution set and represent it on the real number
line
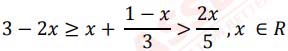
(ii)
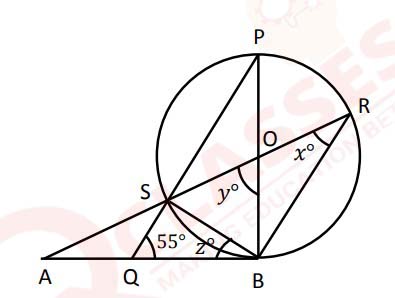
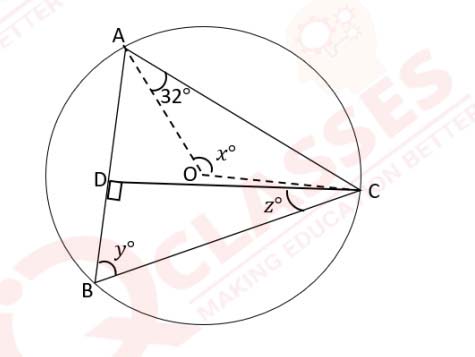
ABCD is a cyclic quadrilateral in which BC = CD and EF is a tangent at A.
∠CBD = 43° and ∠ADB = 62°. Find:
(a) ∠ADC
(b) ∠ABD
(c) ∠FAD
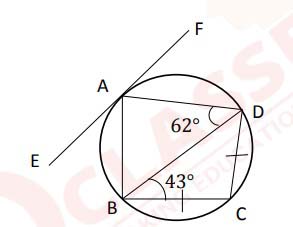
(iii) A (a, b), B(-4, 3) and C(8,-6)are the vertices of a ∆ABC. Point D is on BC such that
BD : DC is 2 : 1 and M (6, 0) is mid point of AD. Find:
(a) coordinates of point D.
(b) coordinates of point A.
(c) equation of a line passing through M and parallel to line BC.
Solution
View
Solution
Question 9
(i) Using componendo and dividend, find the value of x, when:
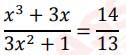
(ii)The total expense of a trip for certain number of people is ₹18000. If three more people join
them, then the share of each reduces by ₹3000. Taking x to be the original number of people,
form a quadratic equation in x and solve it to find the value of x.
(iii) Using ruler and compass only construct ∠ABC = 60°, AB = 6 cm and BC = 5 cm.
(a) construct the locus of points equidistant from AB and BC.
(b) construct the locus of points equidistant from A and B.
(c) Mark the point which satisfies both the conditions (a) and (b) as P.
Hence, construct a circle with centre P and passing through A and B.
Solution
View
Solution
Question 10
(i) Using remainder and factor theorem, factorize completely, the given polynomial:
2𝑥
3 − 9𝑥
2 + 7𝑥 + 6
(ii) Each of the letter of the word “HOUSEWARMING”" is written on cards and put in a bag.
If a card is drawn at random from the bag after shuffling, what is the probability that the
letter on the card is∶
(a) a vowel
(b) one of the letters of the word SEWING.
(c) not a letter from the word WEAR.
(iii) Use graph sheet for this question. Take 2 cm = 1 unit along the axes.
(a) Plot A (1, 2), B(1, 1)and C (2, 1)
(b) Reflect A, B and C about y-axis and name them as Aʹ, Bʹ and Cʹ.
(c) Reflect A, B, C, Aʹ, Bʹ and Cʹ about x-axis and name them as Aʺ, Bʺ, Cʺ, Aʺʹ, Bʺʹ
and Cʺʹ respectively.
(d) Join A, B, C, Cʺ, Bʺ, Aʺ, Aʺʹ, Bʺʹ, Cʺʹ, Cʹ, Bʹ, Aʹ and A to form a closed figure.
Solution
View
Solution
 and B =
and B = 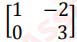

 The value of AB : PQ is:
The value of AB : PQ is:



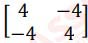 find A
2
. If A
2 = p A, then find the value of p
find A
2
. If A
2 = p A, then find the value of p