Class XII ISC Chapter 3D Exercise 2.7
Explore our extensive collection of Three-dimensional questions, tailored for class 12 students following the ISC curriculum. This topic is vital for understanding how to optimize a particular outcome given certain constraints. Our practice questions cover various aspects of Linear Programming, including formulating linear inequalities, graphical methods, and finding optimal solutions. Whether you're looking to strengthen your problem-solving skills or prepare for your exams, these questions provide the perfect resource to master Three-dimensional concepts with ease.
class 12 Three-dimensional exercise2-7
Three-dimensional
Select Exercise
Q2
Show that the following pairs of planes are at right angles to each other:
(i) 3x-5y+3z-1=0 and 2x+3y+3z=7
(ii) r→(2i^+6j^+6k^) =13 and r→(3i^+4j^ -5k^) +7=0.
Q3
Find the value of p for which the following planes are perpendicular to each other :
(i) r→(pi^+2j^+3k^) =5 and r→(i^+2j^-7k^) +11=0
(ii) x-4y+ pz+3=Oand2x+2y+3z=5.
Q4
(i) Write the equation of the plane passing through origin and parallel to the plane 5x — 3y + 7Z +13 =0.
(ii) Find the equation of the plane through the point (1, 4, -2) and parallel to the plane -2x+y-3z=7.
(iii) Find the equation of the plane with intercept 3 on the y-axis and parallel to xz-plane.
Q5
(i) Find the equation of the plane through the point 3i^ + 4j^ -k^ and parallel to the plane r→(2i^-3j^ +5k^) +5=0.
(ii) Find the equation of the plane passing through the point (a, b, c) and parallel to the plane r→(i^ +j^ +k^) =2.
Q6
(i) Find the angle between the line r→ = (2i^-j^+3k^)+λ(3i^-j^+2k^) and the plane r→(i^+j^+k^) =3.
(ii) Find the angle between the line r→ = 2i^-3j^ +λ(k^) and the plane r→(j^-k^) =7.
Q7
(i) Find the angle between the line
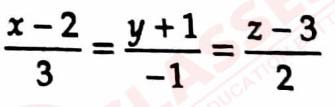
and the plane 3x+4y+z+5=0.
(ii) Find the angle between the line
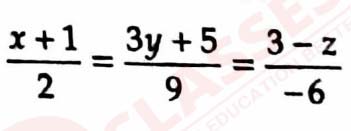
and the plane 10x + 2y - 11z =3.
Q8
(i) If the plane 2x -3y-6z=13 makes an angle sin-1 (λ) with the x-axis, then find the value of λ
(ii) If the angle between the line
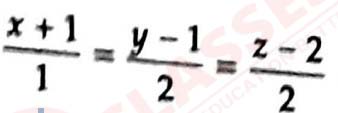 and the plane 2x-y + √λ z=-4 is sin-1 (1/3),find the value of λ
and the plane 2x-y + √λ z=-4 is sin-1 (1/3),find the value of λ
Q9
Inthe following problems, determine whether the given planes are parallel or perpendicular and in case they are neither, find the (acute) angle between them:
(i) 2x+y+3z-2=0 and x-2y+5=0
(ii) 4x + 8y+z-8=0 and y+z-4=0
(iil) 7x + 5y + 6z + 30 =0 and 3x-y- 10z+4=0
(iv) 2x - 2y + 4z +5 = 0 and 3x -3y +6z-1=0
Q10
Prove that the plane 2x + 3y - 4z = 11 is perpendicular to each of the planes x+2y+2z-7 =O and 5x + 6y+7z = 23,
Q11
Find the equation of the plane passing through the points(1,-1,2),(2,-2,2) and perpendicular to the plane 6x - 2y + 2z = 9,
Q12
(i) Find the equation of the plane through the point (1, 2, 3) and perpendicular to each of the planes x + y + 2z = 3 and 3x +2y+z=4,
(ii) Find the equation of the plane passing through the points 2i^ - 3j^ + k^,5i^+2j^-k^ and perpendicular to the plane r(i^ -4j^+5k^) +3=0.
Q13
Find the equation of the plane through the point (1, 2, 3) and perpendicular to the planes x+y+2z=3and 3x+2y+z=4
Q14
Find the equation of the plane through the point i^ - 3j^ -2k^ and perpendicular to the planes r→(i^ +2j^ +2k^) =5 and r→(3i^ +3j^ +2k^) +7=0.
Q15
Find the vector equation of the plane passing through the point 5i^ + 2j^- 3k^ and perpendicular to the line of intersection of the planes r→(2i^ -j^ + 2k^) = 0 and r→(i^ +3j^ -5k^) +7=0.
Q16
Find the equation of the plane passing through the points (2, 3, 1) and (4, -5, 3) and parallel to x-axis.
Q17
Show that the equation ax + by + d = 0 represents a plane parallel to the z-axis. Hence find the equation to a plane through the points (2, -3, 1) and (-4, 7, 6) and parallel to z-axis.
Q18
Show that the equation ax + cz + d = 0 represents a plane parallel to y-axis. Hence find the equation to a plane through the point (3, -5, -2), which makes intercept - 4 on x-axis and is parallel to y-axis.
Q19
Find the equation of a plane passing through the point (2, -1, 5), perpendicular to the plane x+2y-3z=7 and parallel to the line
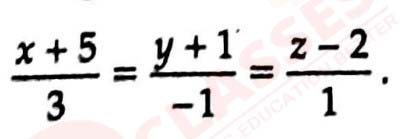
Q20
Find the cartesian equation of the plane passing through the intersection of the planes x + 2y-3 = 0 and 2x -y +z =1 and the origin. Also, write the equation obtained in vector form.
Q21
Find the equation of the plane which is perpendicular to the plane 5x+3y+6z+8=0 and which contains the line of intersection of the planes x + 2y + 3z-4=0 and 2x+y-z+5=0.
Q22
Find the equation of the plane passing through the line of intersection of planes 2x + 3y - z + 1 = 0 and x + y - 2z + 3 = 0 and perpendicular to the plan, 3x — y- 2z - 4 =0. Also find the inclination of this plane with the xy-plane.
Q23
Find the equation of the plane through the line of intersection of r(2i^-3j^+4k^)=1 and r(i^ - j^) +4=0 and perpendicular to the plane r(2i^ - j^ + k^) +8 =0. Hence, find whether the plane so obtained contains the line x - 1 = 2y - 4 = 3z - 12.
Q24
Find the equation of the plane passing through the line of intersection of the planes 2x+y-z=3,5x—3y + 4z+9 =0 and parallel to the line
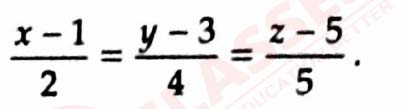
Q25
Find the equation of the plane which contains the line of intersection of the planes x +2y + 3z-4=0and 2x + y—z +5 =0 and whose x-intercept is twice its z-intercept. Hence, find the vector equation of the plane passing through the point (2, 3, -1) and parallel to the plane obtained above.

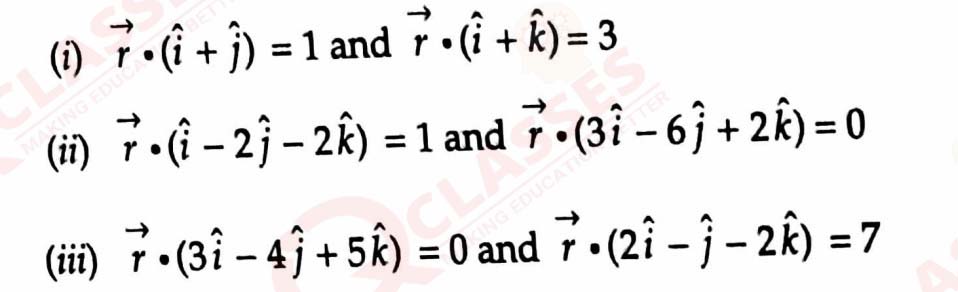

Add a comment